磁路与电路的对偶性案例:绝缘磁芯变压器
曹 磊 周泽森 杨 军
(华中科技大学 电气与电子工程学院, 武汉 430074)
电路模型和磁路模型是电气工程专业课中分析解决实际问题的重要手段,在“电路理论”“电机学”课程的部分章节里有所提及。但由于缺乏系统地论述,学生对于两者之间的区别和联系掌握不够透彻。众所周知,电路和磁路有共通性,比如电动势和磁动势、电流和磁通,电阻和磁阻,以及相应的欧姆定律、基尔霍夫定律等。但两者又有差异性,比如电路中电阻通常是恒定的,而磁路中磁阻存在饱和效应。在变压器中,电路和磁路的关系能够得到较好体现,本文以一种具有特殊结构的变压器(绝缘磁芯变压器)为例,充分利用磁路与电路之间的对偶性,系统地建立其等效电路模型,用于电压和电流分析。通过这一案例,学生能够深入理解并利用对偶性解决实际问题。
1 绝缘磁芯变压器
在工业辐照用低能电子加速器中,绝缘磁芯变压器作为稳定、高效的电源,将低压交流信号升压后输出,再经整流后串联,从而获得直流高压(几百千伏),用于加速电子,具有高效、安全、紧凑的特点。不失一般性,本文以含两个磁芯柱(记为A和B)的绝缘磁芯变压器为例进行讨论,其二维剖面结构如图1所示。初级线圈P排列在最下方,次级线圈S由下到上依次排列,为简化磁路以及相应的电路规模,本文以只含有两个次级线圈的变压器为例进行分析(同时忽略了整流电路部分)。图中φAmp、φBmp分别表示两磁芯柱初级线圈周围处的磁通,φAm1、φAm2、φBm1、φBm2分别表示各次级线圈周围的磁通,φAs1、φAs2、φBs1、φBs2分别表示空气中不同位置处的漏磁通。相邻磁芯通过绝缘材料分隔(阴影部分)。由于绝缘层材料的相对磁导率为1,与同样尺寸的磁芯材料相比,绝缘层具有高的磁阻,引起磁动势下降,从而产生一部分的漏磁损耗(相对较大)。另一方面,与传统变压器一样,主磁通流经各次级磁芯时也会产生漏磁损耗(相对较小)。因此,该变压器中包含了两种不同类型的漏磁,是学生学习磁路-电路对偶特性典型代表。
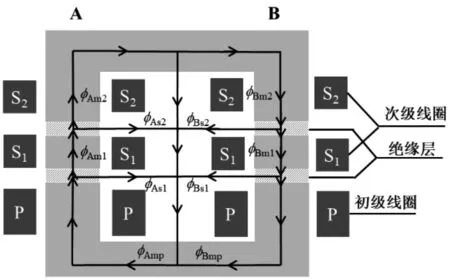
图1 绝缘磁芯变压器的二维剖面结构
本文针对绝缘磁芯变压器设计过程中的实际问题:已知绝缘磁芯变压器的尺寸、材料、线圈参数以及初级线圈所接交流电压源参数,如何计算得到各次级线圈在空载及有载情况下的输出电压?对于这一电参数问题的直接求解,从理论上来说需要建立其电路模型,然后利用合适的电路分析方法进行求解。然而,该变压器存在两种不同种类的漏磁,直接建立电路模型比较困难。本文依据磁力线分布特点,先建立等效磁路模型,然后利用磁路与电路之间的对偶性原理,最终变换得到电路模型。
2 磁路模型
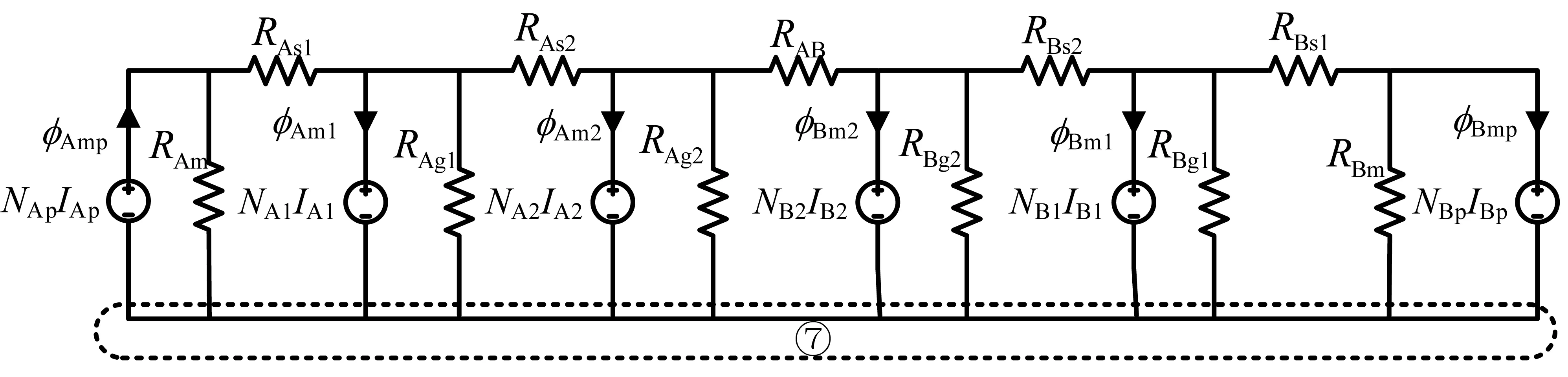
首先对图1所示绝缘变压器中的磁通分布进行分析,从而推导其磁路模型。在磁芯柱A对应的初级线圈P处施加励磁电流后,磁力线会依次经过次级线圈S1、S2,最后经过上磁轭后回到下磁轭完成闭合。需要指出的是,不同磁芯之间的线圈以及相同磁芯线圈之间的漏磁通具有交联部分,因此这部分漏磁通对应的漏电感是相互耦合的。根据磁通分布,可以直接画出其等效磁路模型,如图2所示。其中,RAm、RBm是初级绕组产生的励磁阻,RAg1、RAg2、RBg1、RBg2分别是由相应气隙及周围磁芯带来的等效漏磁阻,RAs1、RAs2、RBs1、RBs2是传统变压器中普遍存在的相邻线圈之间的等效漏磁阻,RAB是A和B磁芯柱最上层的两个次级线圈之间的等效漏磁阻。NApIAp和NBpIBp分别是A、B两磁芯柱初级线圈产生的磁动势,相应的NA1IA1、NA2IA2、NB1IB1、NB2IB2是各次级线圈磁动势。磁路中各磁动势和磁阻之间的串、并联关系可以根据磁力线的走向直接得到。可以看出,绝缘磁芯变压器的等效磁路模型是磁动势先串联气隙漏磁阻(或励磁阻)再并联相邻线圈漏磁阻,如此往复。
3 等效电路模型
“电路理论”中关于电路的对偶特性有相关论述,其中之一是结点和网孔的拓扑对偶性[1]。借鉴该方法,对图2中的磁路模型进行处理,其中有6个独立网孔,分别编号为1~6,如图3(a)所示。该方法的具体过程如下:
第一步:拓扑结构的对偶变换,将6个独立网孔转换为独立结点。已知具有n个结点的电路,其中的任意n-1个结点是相互独立的[2-3],因此除了6个独立网孔外,还需要选取一个非独立网孔。这里选择最外围的回路(虚线所示)。通过网孔到结点的对偶变换得到的磁路无向拓扑结构共含有7个结点,如图3(b)所示,其中结点7通常选为参考结点。
第二步:根据拓扑结构确定关联结点之间的元件。在图3(a)中用一条线连接任意两结点,要求该线通过且仅通过一个磁路元件,将该磁路元件放置在图3(b)相应的两结点之间。该操作使得原先并联(串联)的元件连接形式拓扑对偶变换为串联(并联)的形式,最终可以得到图3(c)所示的拓扑变换后的磁路模型。
第三步:磁路变量(元件)的对偶变换。将磁路中的磁阻变为磁导、磁导变为磁阻,磁势变为磁通,磁通变为磁势,图3(c)的磁路模型变换后的结果如图3(d)所示。
第四步:磁通(电流)归一化。已知实际的初级线圈端口输入电流为IAp,而现有磁路模型中输入磁通为NApIAp,因此需将图3(d)中的磁通NApIAp除以初级线圈匝数NAp。为保证磁路中各支路端口特性不变,所有源支路磁动势不变,磁通均除以NAp,所有磁阻均乘以NAp,结果如图3(e)所示。
第五步:磁势(电压)归一化。已知实际的初级线圈端口电压为VAp,与磁路中的磁链ΨAmp有关。为获得ΨAmp,将初级线圈两端的磁势φAmp乘以NAp变成磁链ΨAmp。同样为了保证各支路端口特性不变,所有源支路的磁通不变,磁动势均乘以NAp,所有磁阻均乘以NAp,结果如图3(f)所示。


图2 绝缘磁芯变压器A、B两磁芯柱的等效磁路模型

(a) 对磁路模型中的网孔进行编号
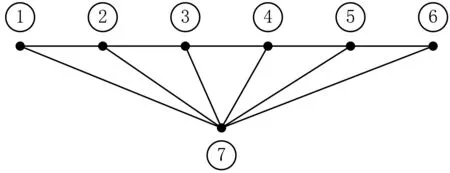
(b) 网孔-结点变换后的无向拓扑结构
(c) 确定拓扑结构结点之间的元件

(d) 磁路参量的对偶变换

(e) 磁通(电流)归一化

(f) 磁势(电压)归一化

(g) 对偶变换后的电路模型图3 利用磁路-电路对偶变换将磁路转换为电路的过程
现在可以回答前文提出的问题:在已知磁元件参数的情况下,能够利用磁路与电路的对偶变换得到电路模型,从而计算出各次级输出电压。需要指出的是,绝缘磁芯变压器中漏磁通有交联部分,因此漏电感之间是相互耦合的。电路模型中的全部元件参数(包括互感)均可以通过磁场仿真或者开路/短路试验准确获得,这超出了本文的讨论范围。
3 结语
本文利用磁路与电路的对偶性,以绝缘磁芯变压器为例,建立了由电感和理想变压器构成的等效电路模型,总结如下:
(1)与电路一样[5-6],磁路元件和拓扑结构也满足对偶关系,例如磁阻和磁导、磁动势与磁通、结点和网孔、串联与并联等;
(2)磁路和电路之间的对偶性体现在:磁路中的磁链对偶变换为稳态电路中的电压;磁路中的磁通对偶变换为电路中相同大小的电流;磁路中的磁阻对偶变换为电路中的电感。以磁路模型为基础,本文利用通用、系统的磁路-电路对偶变换方法,得到绝缘磁芯变压器的等效电路模型,该方法同样适用于其他类型的平面磁路结构,是学生掌握电路对偶、磁路对偶以及磁路和电路之间的对偶性的典型案例。

