霍尔传感器磁路结构仿真分析与优化
宁波中车时代传感技术有限公司,浙江宁波 315021
一、引言
随着信息化时代的发展,作为前端信号检测的关键器件——传感器凸显的作用越来越明显。霍尔电流传感器就是其中一种,广泛应用于轨道交通、工业变频、光伏及汽车等行业[1-2]。
霍尔电流传感器可分为磁路、敏感元件及电路三个部分。此前,对于电路设计、磁路设计以及霍尔敏感元件的应用多有研究,其中电路设计以及霍尔应用部分研究较为深入,而磁路部分则多以规则等截面磁路为研究对象,通过磁电等效的方式对磁路进行简化计算,对于不均匀截面的磁路结构未能深入计算分析[3-4]。
本文以一款方形母排穿心孔的闭环霍尔电流传感器磁路结构作为研究对象,分析不均匀磁路结构的磁场分布及影响传感器性能的关键要素,从而进行改善和优化,提升传感器的性能。
二、传感器原理及磁路结构
1、传感器的工作原理
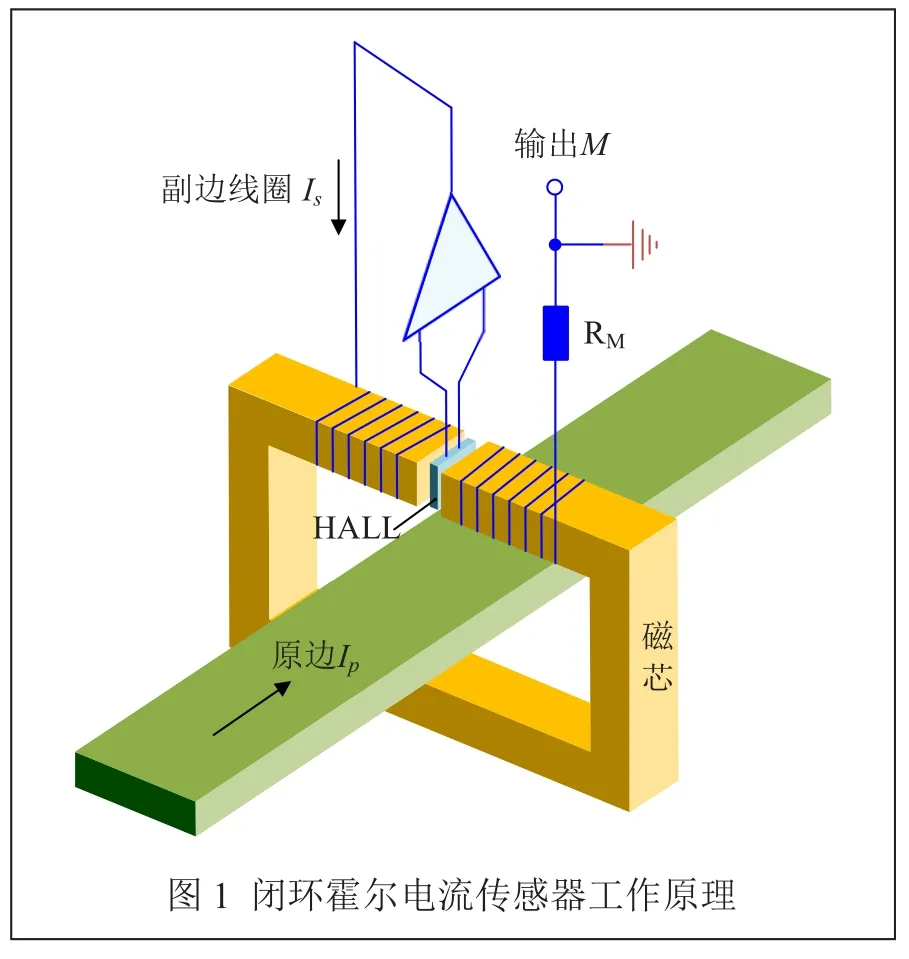
闭环霍尔电流传感器通过副边线圈的电流对原边电流的反馈跟随,在磁路中两者产生的磁场相抵消后使得气隙处的霍尔器件(HALL)始终处于零磁通的状态。
图1所示为传感器工作原理图,当原边电流在磁路中产生磁场时,副边线圈会产生对应大小的电流使得磁路中产生相反方向的磁场,并与原边电流产生的磁场相抵消,使气隙处的磁场处于零磁通状态。原、副边线圈匝数已知时,通过副边线圈测量得到的电流大小就可以计算出原边电流大小[5-6]。
2、叠片铁芯的磁路结构
传感器的现场应用环境是复杂多样的,包括安装接口以及原边电流的载体铜母排尺寸形状也各不相同。扁平状铜母排是现场应用中较为常见的一种,故而传感器的母排穿心孔设计成扁平状截面。同时为了遵循传感器小体积设计原则,整个磁路设计成扁平矩形结构,从而减小传感器整体的体积。
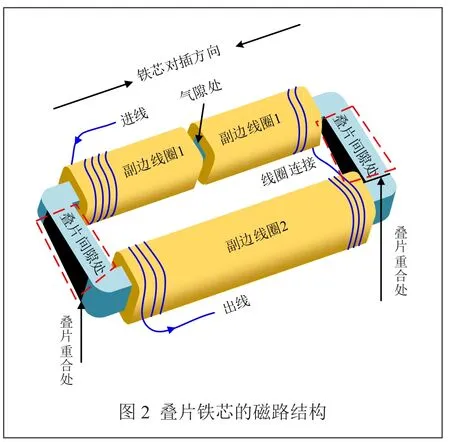
由于矩形磁路的线圈整体绕制较为复杂,故而采用分体式线圈磁路结构。即先绕制平直线圈,再将叠片铁芯进行对插后组装成磁路结构。图2所示为传感器叠片铁芯磁路结构示意图。单片的C型铁芯分别从两侧依次对插到副边线圈1和副边线圈2中形成传感器的磁路。副边线圈1中间为气隙处,气隙两侧为不重叠铁芯,副边线圈两侧为叠片铁芯交叉重叠处,磁路另外两边的铁芯因一侧为单组另一侧为两组交叉而形成叠片间隙。
三、磁路分析计算
1、叠片铁芯的磁场计算
若电路中的两点间存在电位差,则这两点间可能产生电流。同样,在磁路中两点间存在磁位差,则这两点间可能产生磁通。可利用类似于电路的电位分析法对磁路进行分析,从而了解漏磁的分布[7]。
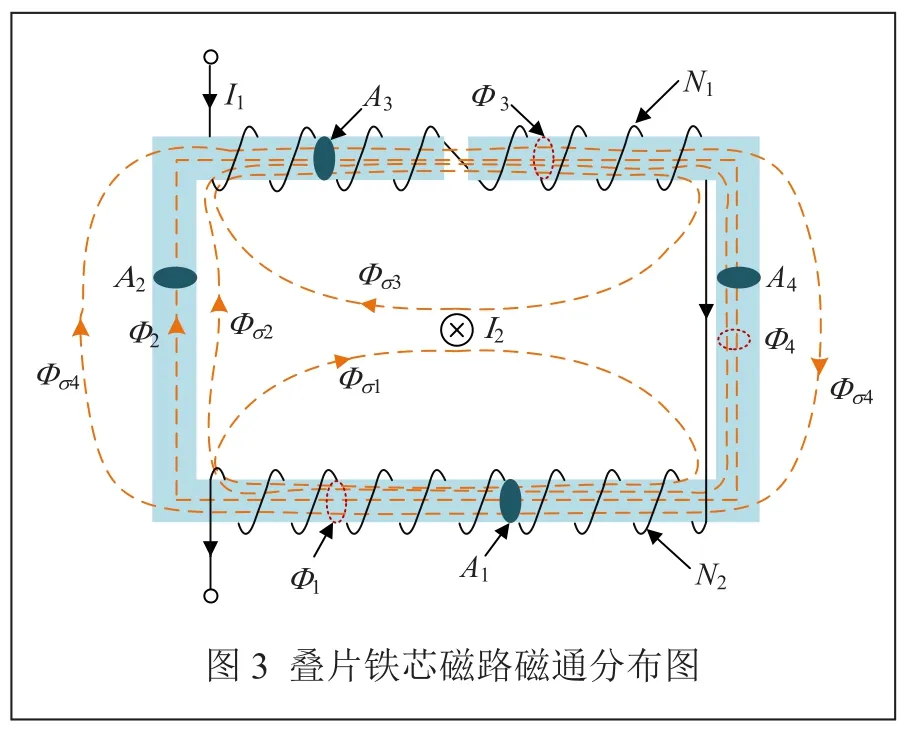
如图3所示为叠片铁芯磁路中的磁通分布示意图。
由于副边线圈集中绕制在磁路的上下两边,线圈产生的磁通被磁芯短路,磁势落在周围空气,漏磁主要集中在线圈两端,分别是线圈两端之间的漏磁Φσ1、Φσ3以及两线圈之间的漏磁Φσ2等。同时,因磁路左右两侧的叠片铁芯之间存在着间隙,故而也会产生漏磁Φσ4。铁芯的截面分别是A1、A2、A3以及A4,铁芯内部经过的磁通分别是Φ1、Φ2、Φ3、Φ4。副边线圈电流大小为I1,上边线圈匝数为N1,下边线圈匝数为N2,原边电流大小为I2。
根据磁路的基尔霍夫定律,磁路中的任意节点的磁通之和等于零,有:

于是有:

根据安培环路定律,在电流产生的磁场中,磁场强度H沿着任意封闭的曲线进行积分所得到的值等于此封闭的曲线中包围的所有电流之和,即:

于是有:
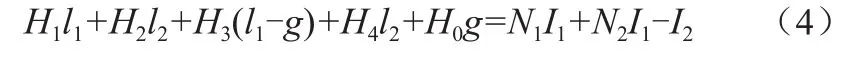
其中,H1、H2、H3、H4—分别为磁链上磁通Φ1、Φ2、Φ3、Φ4对应的磁场强度;
H0—气隙处磁场强度;
l1、l2—矩形磁路的长、宽尺寸;
g—气隙大小。
根据磁通和磁场强度之间的关系,有:
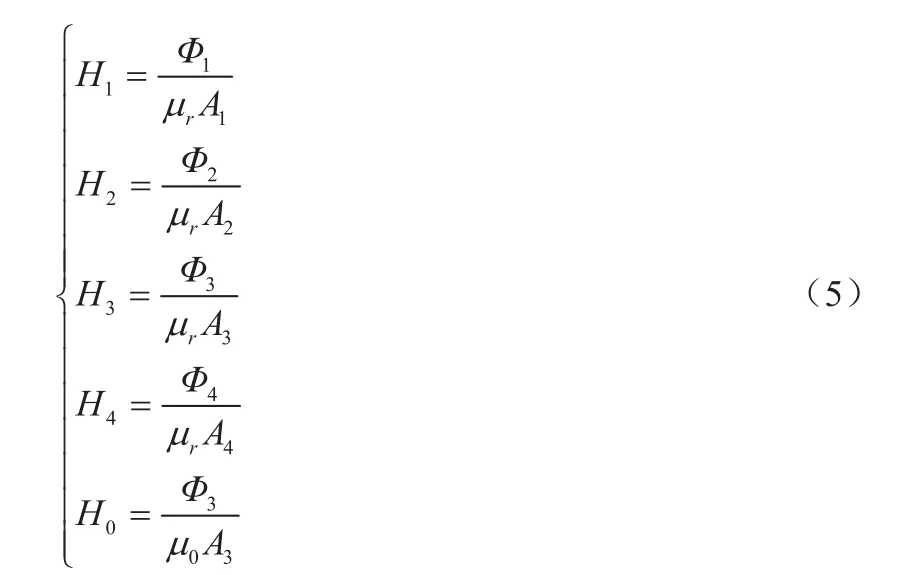
其中,μr—磁芯中的磁导率;
μ0—气隙处的磁导率。
联立(2)、(4)、(5)可得气隙处的磁感应强度为:

其中,a—常系数;
b、c—和磁路截面积相关的系数;
Φσ—等效漏磁通。
由式(6)可见,传感器磁路气隙中的磁感应强度与磁路叠片间隙引起的漏磁、磁路各个磁链的截面积有关,下面结合Maxwell仿真软件针对磁路进行仿真分析。
2、叠片铁芯的磁场仿真
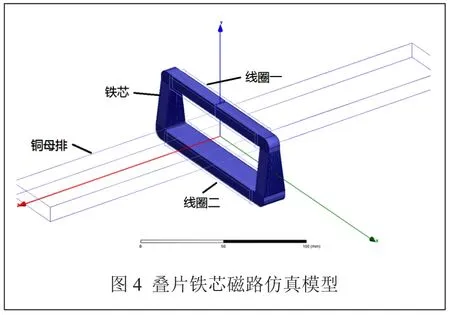
Ansoft Maxwell是在低频电磁场领域中著名的有限元软件之一,广泛应用在各个工程电磁领域[8]。结合Maxwell仿真软件,对现有模型进行仿真分析,模型创建后如图4所示。
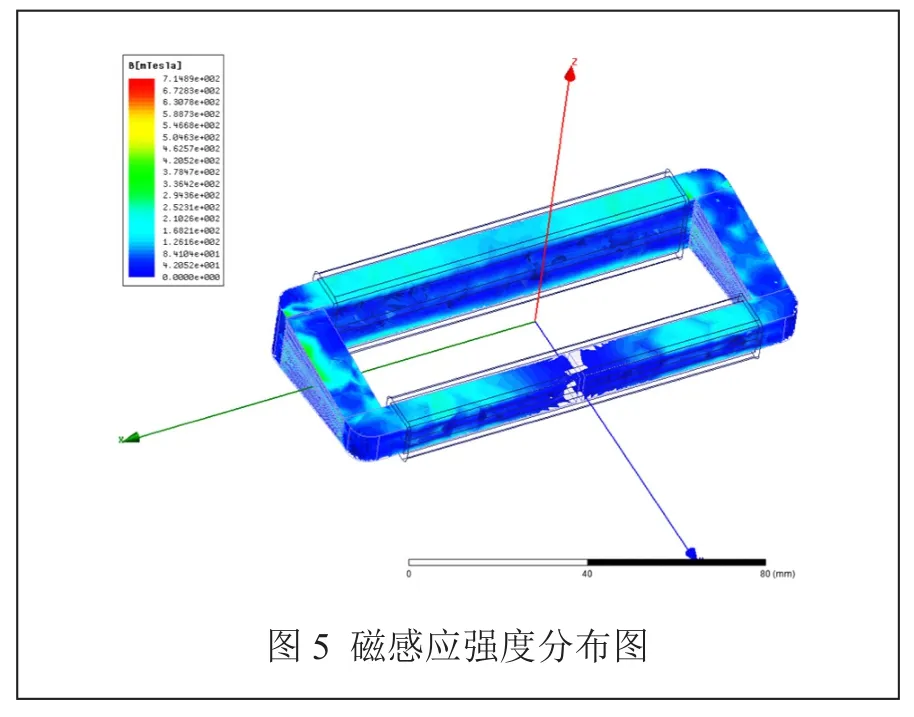
铜母排上施加原边电流激励,大小从0A到1000A,以100A线性递增。线圈1和线圈2上施加副边电流激励,原副边之间的安匝比相等,对于磁场中产生的磁感应强度方向相反,对模型进行静电磁场求解,得到如图5的磁场磁感应强度分布图。
图5中所示为原边电流1000A时磁路中的磁感应强度分布图,由图中可以看出,气隙处的磁感应强度较小。而从理论上来说,当气隙的磁感应强度为零时,副边线圈电流才能精确地反应原边电流的大小,故而需考察气隙处的磁感应强度。取气隙中间点作为研究对象,提取仿真结果如图6所示。
由图6可知,气隙处的磁感应强度随着电流的增大而增加。可见,叠片对插磁路中由于漏磁、截面积不均匀等因素的影响,造成当原副边安匝比相等,产生磁通方向相反时,气隙中还能产生磁感应强度,不能满足零磁通的要求,从而影响产品的测量精度等基本性能。

3、磁路模型优化
由上述分析可知,影响磁路的主要因素有磁路的铁芯叠片气隙大小、磁路的横截面积是否均匀等。基于此考虑,结合现有的生产制造能力,对原有的磁路结构进行优化设计,减小叠片间的气隙影响,同时使得环路上的截面积均匀。
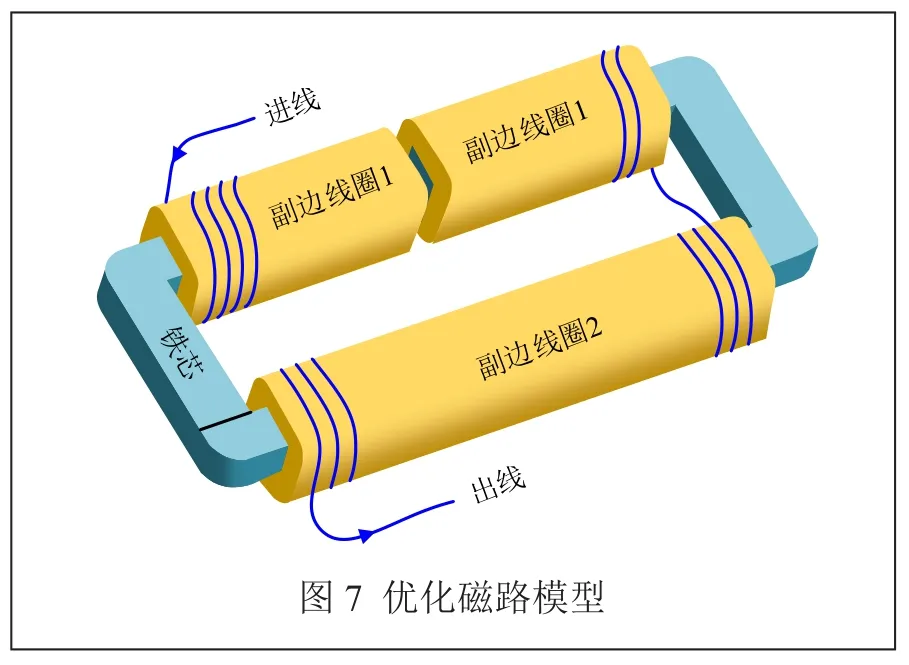
图7所示为优化后的磁路模型图。由于原先的C型铁芯对插后所产生的中间叠片间隙以及截面积不均匀,故而为使铁芯能够紧密贴合,采取L型和C型铁芯进行对插的结构方案,层间交叉叠片,从而使得整体铁芯磁路平整,层间紧密贴合,避免产生叠片间隙,同时也使得优化后的磁路各个截面积均匀分布。
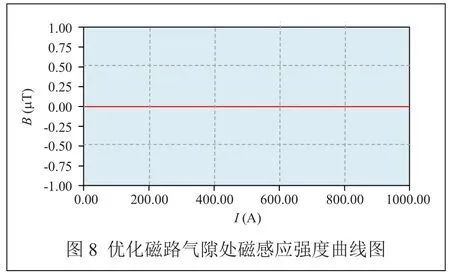
采用Maxwell对优化后的磁路模型进行仿真分析,施加的原副边电流激励和原仿真模型的激励相同。取气隙处相同点作为研究对象,提取仿真结果如图8所示。
从图8中可以看出,气隙处的磁感应强度基本稳定在零附近,说明通过磁路的结构优化设计,来改善原先磁路结构存在的不足之处,利于产品性能的提升。
四、传感器样机验证
为了验证优化后的磁路对产品性能的提升,分别对传感器样机以及安装优化结构磁路后的传感器样机进行测试,收集数据分析基本误差、线性度等基本性能,从而判断磁路结构优化的实际状态。
样机的基本参数:
额定测量电流:1000A;
测量范围:0A~±2000A;
额定测量输出:200mA;
精度:<±0.5%;
线性度误差:<0.1%。
将传感器原边输入电流从0A到1000A,以200A为一个测试点记录输出,表1为原有传感器经过零点调试之后的数据,表2为装配后无需调试直接测试的数据。从表中可以看出,结构优化后的精度σ由0.107%提升至0.040%以上,而零点输出稳定性、线性度等基本性能也均得到提升,同时减少了零点调试的工序。
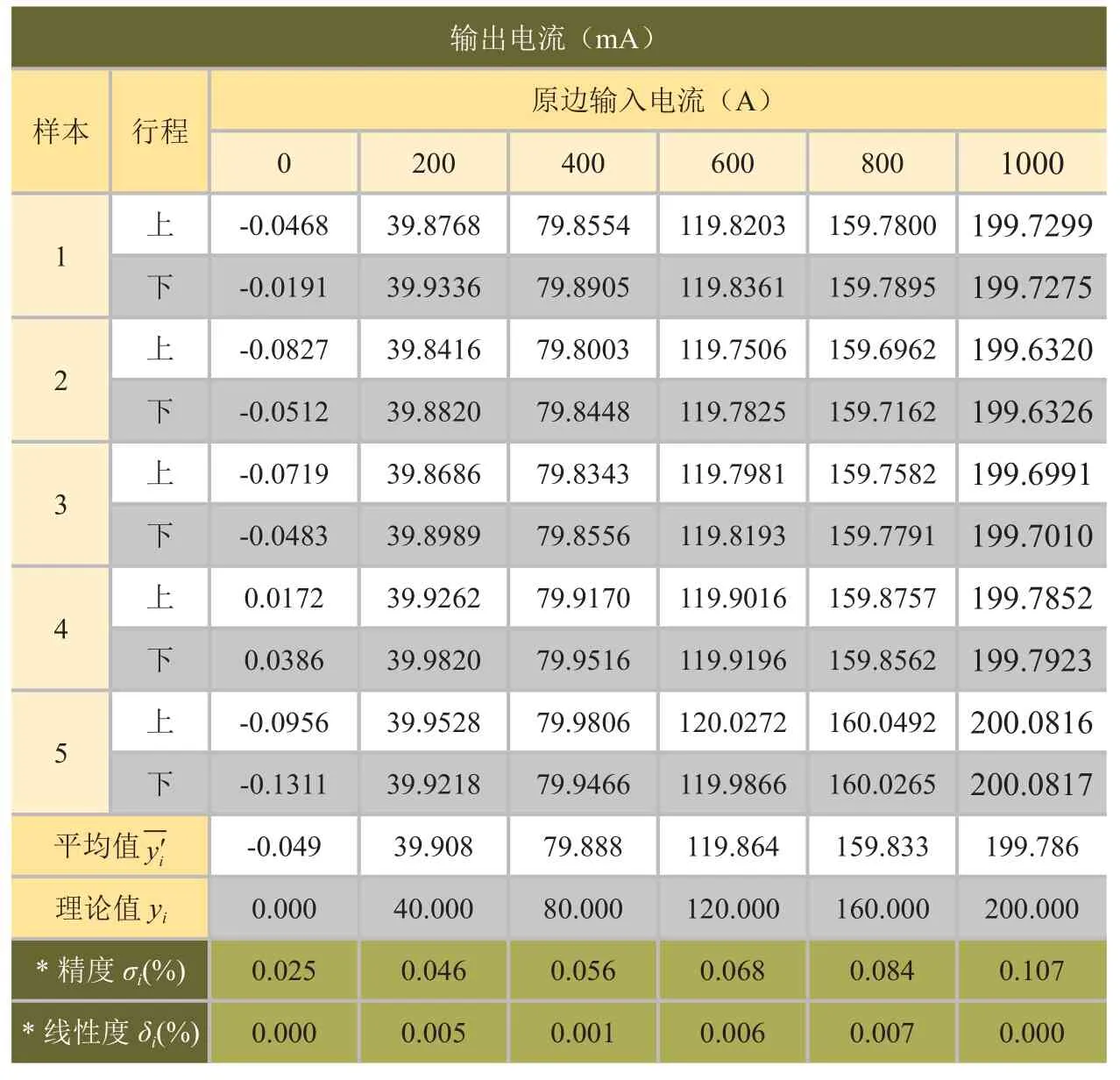
表1 原有传感器基本性能测试数据
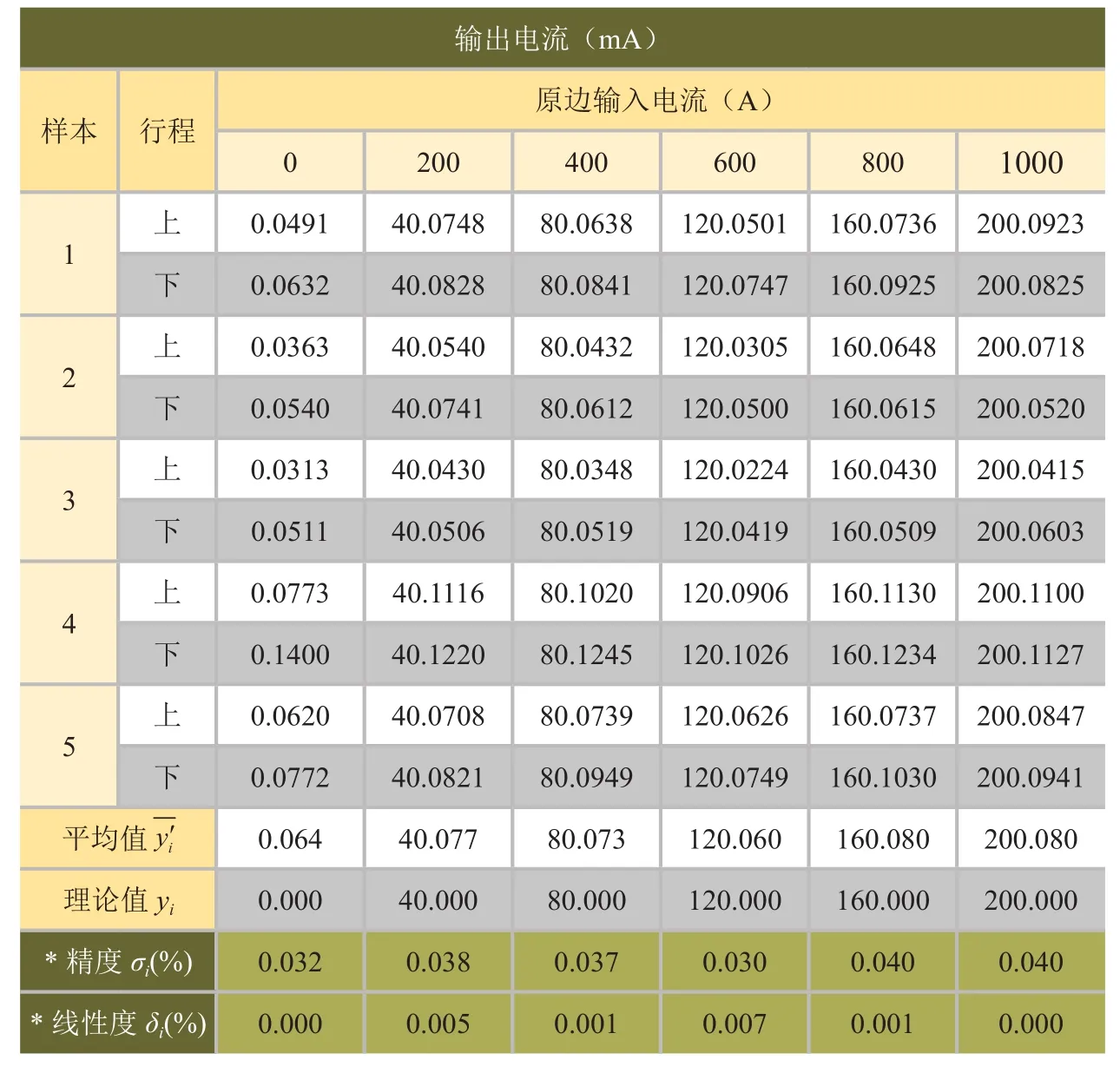
表2 改造后传感器样机基本性能测试数据
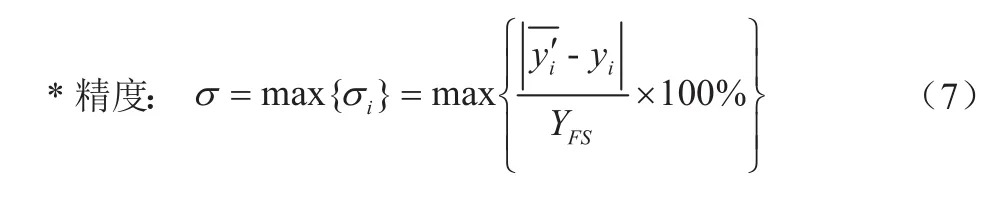
yi—传感器在第i个测量点上的输出理论值;
YFS—满量程理论输出值。

y"i—拟合直线上第i个点的值;
YFS—满量程理论输出值。
拟合直线采用端基法,其直线方程为:

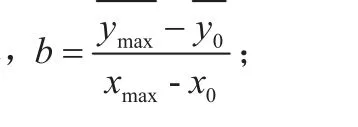
a—端基直线截距
—传感器测量上限实际输出信号的平均值;
—被测量为零时传感器的实际输出信号的平均值;
xmax,x0—传感器测量上限输入值和零输入值。
经过计算,表1拟合直线方程为y"=-0.049+0.199835x,表2拟合直线方程为y"=0.064+0.200016x。
五、结论
本文主要通过对现有叠片C型对插铁芯的磁路结构进行理论计算和仿真分析,提出了现有磁路的不足以及影响产品基本性能的关键因素,在此条件上进行结构优化,采用L+C型叠片铁芯,从而改善磁路,提升产品基本性能。主要包括如下:
(1)优化磁路结构,避免原
先磁路中因叠片结构造成的两侧间隙,使得铁芯层与层之间叠片紧密,减少磁路中的漏磁通的影响;
(2)采用L+C型的叠片铁芯结构,使得铁芯叠片之后的磁路截面积均匀,同时也减小了整个磁路的体积,使得产品性能稳定的同时实现小体积;
(3)通过优化磁路结构,改善产品的基本性能,精度从0.107%提升至0.040%以上,同时使得产品零点稳定,批量生产一致性好,缩减了产品调试过程中的大量工时,利于在产品生产制造的同时降低生产成本,实现降本增效。

