叠片过滤器水力和过滤性能综合评价方法研究
杨培岭,鲁 萍,任树梅,王 枭,刘伟杰
(中国农业大学水利与土木工程学院,北京100083)
0 引 言
灌水器过滤器是保证滴灌系统不受堵塞,能够正常运行的核心设备[1-2]。由于其占地面积小、自动化程度高,同时又兼具筛网和砂石过滤器的特点,能够实现立体过滤,叠片过滤器在过滤系统中得到广泛应用[3],但其流道结构较为复杂,运行过程中常伴有较大的水头损失。因此选择合适的叠片过滤器产品是提高过滤性能的最有效方法。
叠片的结构是影响过滤性能的最主要参数,但因其属于微尺度范畴,目前开展的研究仅限于数值模拟领域。李楠等[4]对叠片过滤器的流道进行了三维造型,采用标准k-ε 模型进行数值模拟计算,结果发现,叠片流道最小断面底角以及叠片厚度影响过流能力,而叠片流道的倾斜角度对过滤器的水头损失几乎没有影响。张重[5]对叠片流道断面进行了简化的koch 分形设计,结果表明1/2处梯形分形流道最易于泥沙的沉积。马子萱[6]运用一级Minkowski分形曲线设计叠片流道沿程轴线,认为更长的流道长度具有更好的过滤性能。叠片过滤器的过滤性能难以直接通过叠片结构尺寸来判断,但目前尚无明确的评价方法。
影响过滤过程的因素很复杂[7],大多学者通过对叠片过滤器进行性能测试试验,采用运行周期、泥沙去除率、水头损失等[8-11]指标来评价其性能优劣,但评价指标单一,不能综合地反映过滤性能。研究发现[11-13],叠片过滤器水头损失均表现出随系统运行先线性缓慢增长后线性加速递增的动态变化特征,而不同运行时段水头损失的变化规律在一定程度上能够反映杂质颗粒在叠片流道内堵塞的均匀性;另一方面,不同的叠片过滤器其叠片结构存在差异。因此,本文提出基于叠片结构尺寸参数的叠片过滤器性能评价方法,旨在为选择合适的叠片过滤器产品提供指导。
1 材料与方法
1.1 试验装置及过滤器
试验装置如图1所示。其中供水装置为2 m×2 m×1.5 m的蓄水池,蓄水池内安装搅拌泵,以保证试验中进水含沙量的稳定。叠片过滤器进出口压差通过压差传感器自动记录,并利用高精度压力表实时校核。电磁流量计用来实时读取系统瞬时流量。
选择5 种常见叠片过滤器,对其进行性能测试,测试时采用相同的额定流量(30 m³/h)、额定工作压力(0.15 MPa),过滤精度(120 μm)、管道进出口直径(63 mm),且所有过滤器采用同一外壳,因此除滤芯不同外,其他均保持一致。叠片主要结构尺寸参数如表1 所示,沟槽外截面及表面示意图如图2所示。

图1 叠片过滤器水力性能试验装置示意图Fig.1 Schematic of device for hydraulic performance test of laminated filter
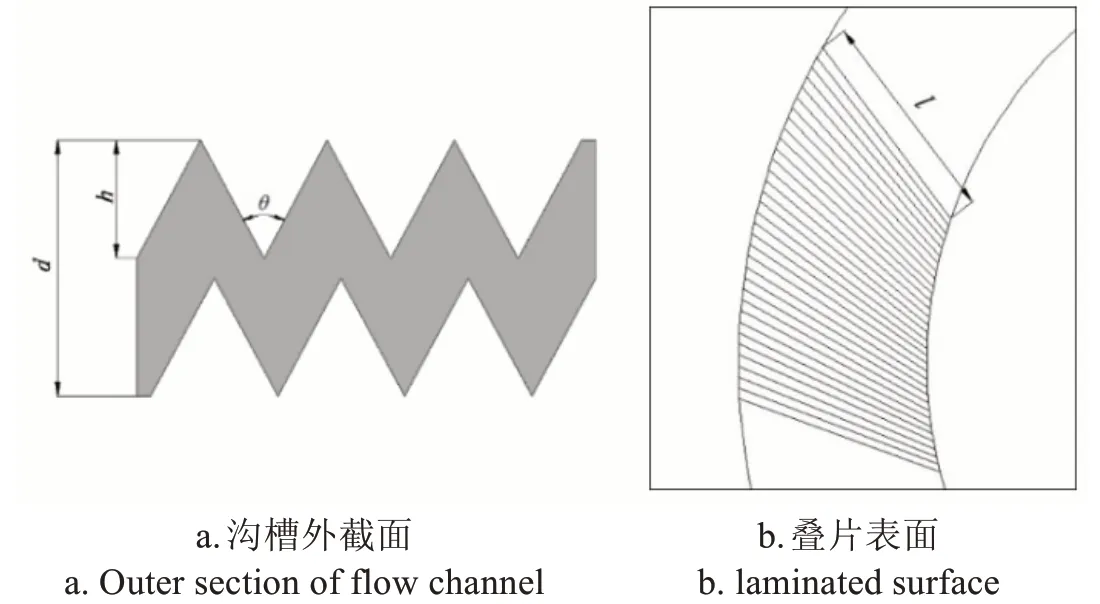
图2 叠片结构示意图Fig.2 Schematic diagram of laminated structure
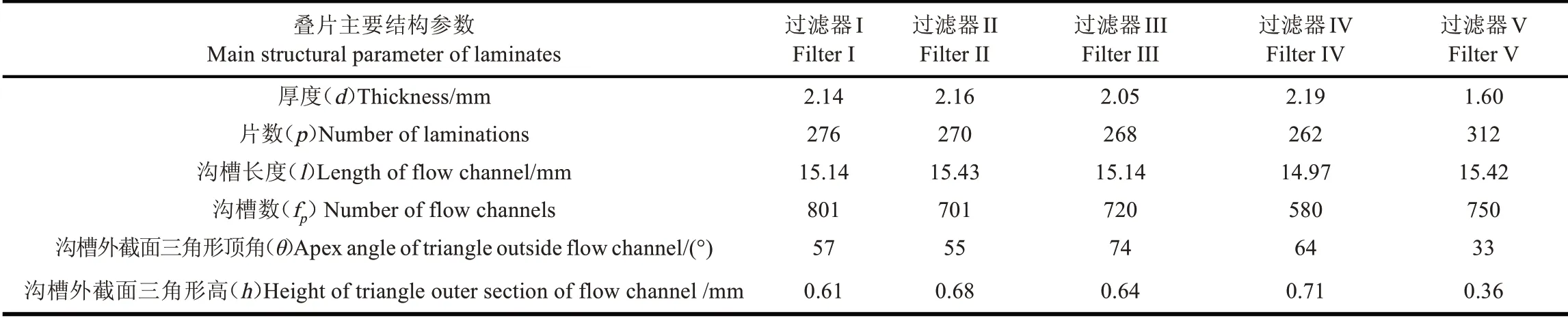
表1 5种叠片主要结构尺寸参数Table 1 Main structural size parameters of 5 laminated filters
1.2 试验设计及过程
为了深入研究叠片过滤器对泥沙的过滤能力,本文进行含沙水试验,配置含沙水中0~10、>10~20、>20~40、>40~80、>80~160、>160~320、>320~1 000 μm 泥沙颗粒占比分别为10.68%、8.94%、22.97%、30.78%、15.03%、6.64%、4.96%。实际灌溉中,灌溉水源经过一级过滤系统,过滤后泥沙粒径均小于0.18 mm[14]。本文采用粒径小于0.16 mm 的细沙,泥沙超过80%(质量分数),符合工程实际。按比例向蓄水池中配置好所需含沙水。试验中,水流由蓄水池进入叠片过滤器,在过滤器内经过滤芯过滤后重新流回蓄水池,以达到循环过滤的效果。
1)相同进水流量不同进水含沙量
为保证灌溉水量,实际大田灌溉中过滤器常采用最大流量[14],故本试验保持进水流量为30 m³/h。根据微灌易堵塞水质标准[15],设置3 个进水含沙量(质量分数)水平0.02%、0.03%及0.04%,其对应的固体颗粒浓度分别为200、300和400 mg/L。
2)相同进水含沙量不同进水流量
过滤器进水流量的大小将直接影响其局部水头损失。试验中,保持相同进水含沙量(0.03%),考虑滴灌系统田间布置以及通过流量的实际情况,分别采用0.8、1.0及1.2 倍的额定流量(25、30 及35 m³/h)3 种进水流量水平,根据系统流量变化测叠片过滤器局部水头损失。
参考灌水均匀度要求,判断叠片过滤器严重堵塞的标准为系统流量下降至初始流量的80%[15],该周期即为叠片过滤器在此工况下的运行周期。
根据前述试验设计对不同叠片过滤器进行性能测试试验,从水头损失动态变化特征、堵塞均匀度、周期拦沙量以及拦截泥沙中值粒径对5种叠片过滤器进行分析。
1.3 评价指标及方法
1.3.1 堵塞均匀度
水头损失增长速率和运行周期是评判过滤器过流能力的重要指标,然而不同过滤器在不同运行阶段表现出相异的变化特征,仅靠水头损失和运行周期大小对过滤器性能进行评价,标准相对宽泛。
本文引用叠片过滤器堵塞均匀度指标(ηu)[16],用以反映堵塞物在叠片沟槽内分布的均匀程度。将过滤器开始运行至水头损失达6~8 m 期间定义为过滤器稳定运行时段(t1),从水头损失达6~8 m 至完全堵塞停止运行期间定义为过滤器堵塞运行时段(t2)。

式中k1和k2分别为t1和t2时段水头损失随时间增长速率,m/h。k2越接近k1,即ηu越接近于1,堵塞物在叠片过滤器滤芯内的堵塞越均匀。
1.3.2 周期拦沙量
过滤器的拦沙量是指在整个过滤周期内,滤芯所截留的沙粒总量,g。本文通过测定叠片过滤器的周期拦沙量来评判其拦沙能力。
1.3.3 拦截泥沙中值粒径
泥沙处理能力是过滤器的一项重要性能指标,主要体现在拦截泥沙粒径上[17]。研究发现,粒径处于50~100 μm范围内的泥沙很容易沉淀在滴灌带的腔体内和流道内,从而引起灌水器的堵塞[18]。因此,叠片过滤器所拦截的泥沙粒径相对小,表明其泥沙处理能力相对好。本文采用叠片过滤器1 次过滤周期内所拦截泥沙的中值粒径(D50)来评判其泥沙处理能力。
1.3.4 综合评价
根据可比性和可行性的原则,本文选择堵塞均匀度(以ηu表示)、周期拦沙量(以M 表示)以及拦截泥沙中值粒径(以D50表示)3项指标来评价叠片过滤器性能。
1)通过线性函数拟合叠片过滤器ηu、M 以及D50值与叠片各结构参数(表1)间的相关关系,分别建立3项指标的多元线性回归方程。2)综合单项性能评价指标与叠片结构参数间的相关关系,根据所建立的回归方程,采用加权组合法中的直接加权法建立叠片过滤器过滤性能的综合评价体系,加权因子根据单项指标函数的变动范围计算确定。
1.4 数据分析方法
数据统计及处理采用Excel2016、SPSS22.0 软件;相关性采用Pearson 相关分析;回归方法采用逐步回归分析,建立叠片结构尺寸参数与过滤器单项性能指标间的相关关系,并利用主成分分析方法消除多重线性相关对回归方程系数的影响;采用加权组合法中的直接加权法建立叠片过滤器性能评价的统一目标函数。
2 结果与分析
2.1 不同叠片过滤器堵塞均匀度及水头损失动态变化的对比
额定流量条件下,不同进水含沙量时5种过滤器水头损失动态变化如图3所示。可以看出,不同叠片过滤器水头损失均表现出随系统运行先缓慢上升后线性激增的变化特征,但不同叠片过滤器线性激增阶段递增速率(k2)存在显著差异,过滤器III、过滤器IV水头损失增长速率较快。从表2中可以看出,过滤器V的ηu值较低,过滤器III、过滤器IV的ηu值较大。总体来说,各过滤器水头损失在达6~8 m后便开始呈现快速增长趋势,可以认为此时过滤器已经发生明显堵塞,这与国内过滤器反冲洗指标[19]相一致。
研究认为,过滤器在水头损失达6~8 m 后出现随时间激增的现象主要是滤芯内堵塞不均匀造成的[17],且随着进水含沙量的增加,堵塞物分布的不均匀性加剧。另外,过滤过程中杂质颗粒间、颗粒与叠片间的吸附作用也会减小滤芯的过流面积,从而影响过滤效果。但随着过滤器运行停止,吸附作用也将随之消失。而杂质在叠片流道内堵塞的均匀程度以及过滤过程中杂质颗粒间、颗粒与叠片间的吸附作用与叠片沟槽的设计及相关尺寸参数直接相关,因此,对于叠片过滤器的过滤性能更应基于叠片尺寸参数来综合评定。
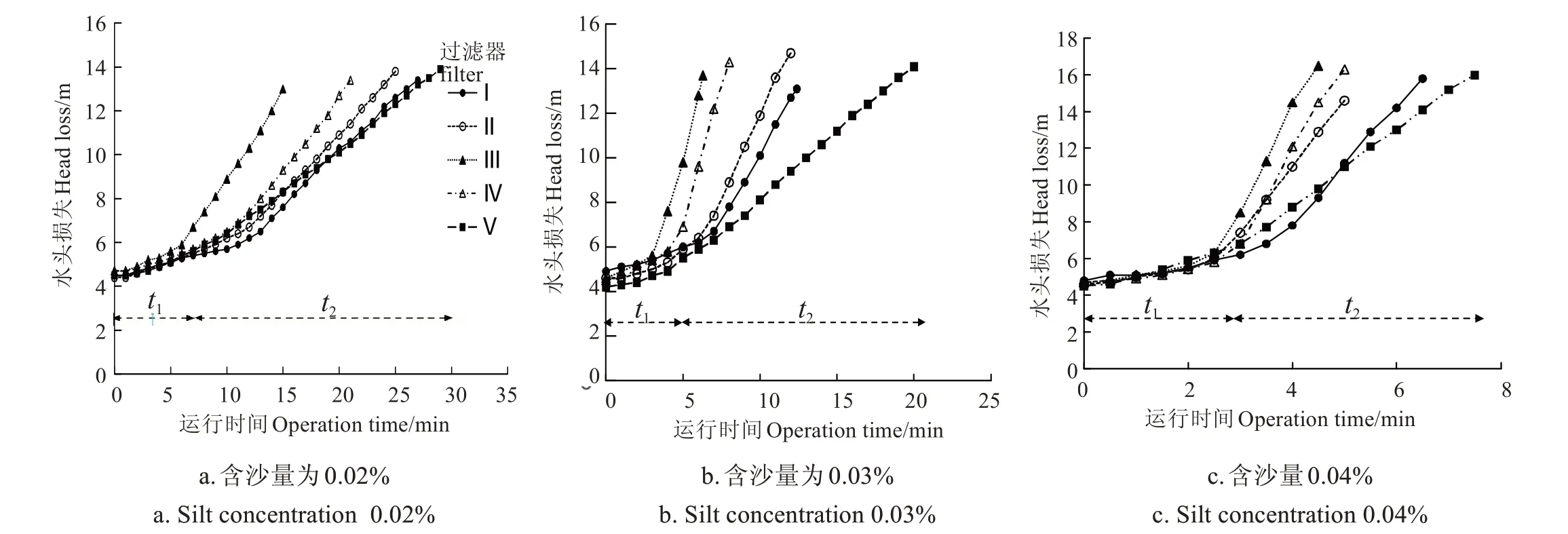
图3 不同含沙水条件下5种叠片过滤器水头损失动态变化Fig.3 Dynamic of head loss of 5 laminated filters under different sand-water conditions

表2 不同进水含沙量条件下不同时段叠片过滤器堵塞均匀度随时间变化线性回归拟合结果Table 2 Linear regression fitting results of filter clogging uniformity varying with time at different period under different silt concentration
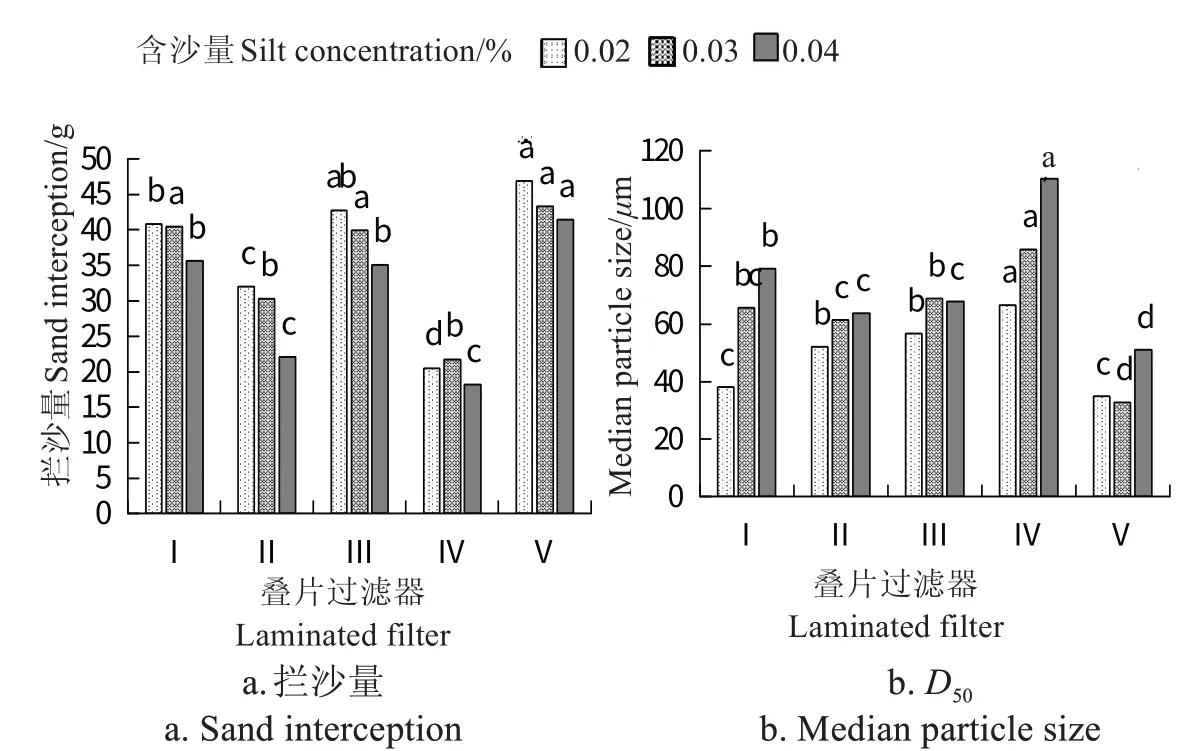
图4 含沙水条件下5种过滤器周期拦沙量和拦截泥沙中值粒径Fig.4 Amount and median size of intercepted sediment by 5 filters under sandy water condition
2.2 不同叠片过滤器拦沙量、拦截泥沙中值粒径对比
图4 为含沙水条件下5 种叠片过滤器的周期拦沙量和拦截泥沙D50。从图中可以看出,不同含沙量条件下,过滤器IV 的拦沙量显著低于(P<0.05)其他4 种过滤器,拦沙能力较差;过滤器V 的拦沙量显著高于(P<0.05)其他过滤器,平均拦沙量高出其他过滤器约23.54%~32.98%,说明过滤器V 能够在过滤周期内拦截质量较多的泥沙;过滤器III、过滤器I 以及过滤器II 的平均拦沙量依次减小。从拦截泥沙D50来看,总体上过滤器V 所拦截泥沙D50值显著低于(P<0.05)其他过滤器,平均值约低33.08%~54.90%,说明其拦截的泥沙中细颗粒含量较多;过滤器IV 拦截泥沙D50值显著高于(P<0.05)其他过滤器,说明过滤器IV 所拦截泥沙中粗颗粒占比较大;总体上来看,过滤器II、过滤器III 拦截泥沙粒径差异不显著。
2.3 叠片过滤器性能综合评价
2.3.1 单项性能评价指标与叠片结构参数间的相关关系
根据上文的分析结果可以看出,不同叠片过滤器的水头损失动态变化特征、堵塞均匀度、周期拦沙量以及拦截泥沙D50均有所差异。因此,按照评价指标中的方法对5 种叠片过滤器进行综合评价。首先通过线性函数拟合5 种工况下,5 种叠片过滤器ηu、M 以及D50值与叠片各结构参数间的相关关系,并将ηu与k2、运行周期(以T 表示)进行比较,相关性结果如表3所示。
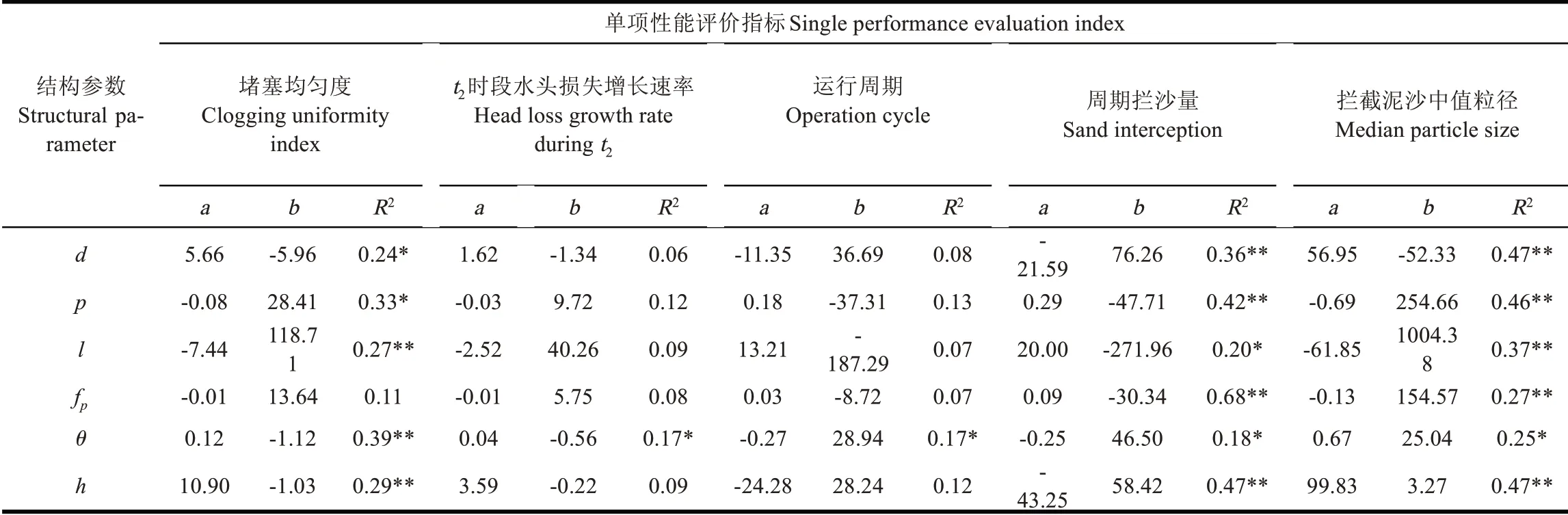
表3 叠片过滤器性能评价指标与叠片结构参数间关系Table 3 Relationship between performance evaluation indices of laminated filter and structural size parameters
从表3 中可以看出,ηu、M、D50值与叠片各结构参数间存在线性相关关系。其中,ηu主要受到d、p、l、θ、h 的影响,ηu值随d、θ、h 的减小而减小,即堵塞更均匀,随p、l的减小而增大,即堵塞均匀度更差;M 和D50值受到6 种结构参数的共同影响,其中,M 值随p、l、fp的增大而增大,随d、θ、h 的增大而减小;D50值随d、θ、h 的增大而增大,随p、l、fp的增大而减小。相比之下,k2和T 值与叠片各结构参数间的相关关系较弱,因此选用ηu、M 以及D50这3 项指标与各自影响因素间建立多元线性回归关系。在对M、D50值的回归分析中,剔除对其影响不显著(P>0.05)的变量,选用逐步回归法进一步确定影响两者的有效因子。经过筛选后,分别有d、fp和l、θ、h 分别对M和D 值影响显著(P<0.05),且回归方程影响极显著(P<0.01),结果见式(2)和式(3)。在对ηu值的回归分析中,回归方程满足显著性要求(P<0.05),但各项系数间存在严重的多重线性相关关系,d 和h 项系数方差膨胀因子(variance inflation factor,VIF)值为22.9 和29.8,均大于10,结果见式(4),这将会对回归方程的系数及其相关性产生影响。为消除多重线性相关对回归方程系数的影响,本文采用主成分分析方法提取由原始变量线性组合的潜在变量,再将所提取的主成分因子与ηu值进行回归分析。
对与ηu值相关的变量d、p、l、θ、h进行主成分分析,提取了1 个主成分Y1(ηu)(见式(5)),该主成分方差贡献率达到83.9%,可以代表对ηu值的评价信息。Y1(ηu)与ηu值的回归方程结果见式(6),方程满足显著性要求(P<0.05)。将标准化变量还原为原始变量,得到ηu值的回归分析方程,结果见式(7)。

表4 叠片过滤器性能评价指标与叠片结构参数间线性回归结果Table 4 Linear regression results between performance evaluation index of laminated filter and structure parameters

式中Y(M)、Y(D)、Y(ηu)分别为对拦沙量M、拦截泥沙中值粒径D50、堵塞均匀度ηu的线性回归结果,Y1(ηu)为Y(ηu)所提取的1 个主成分,Y2(ηu)为ηu消除各变量多重线性相关后的线性回归结果。Y2*(ηu)为Y2(ηu)的标准化量,d*、p*、l*、θ*、h*分别为参数d、p、l、θ、h的标准化量。
2.3.2 基于叠片结构参数的过滤器性能综合评价方法
根据叠片过滤器性能的评判标准,ηu和D50值以小为佳,M 值则越大越好。利用上文所建立的回归方程,采用直接加权法建立评价叠片过滤器性能的统一目标函数,将指标命名为Q,见式(8)。
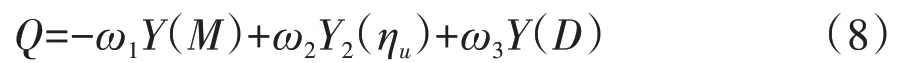
式中Q为叠片过滤器性能综合评价指标函数,下同;ωj(j=1,2,3)表示Y(M)、Y(D)、Y2(ηu)3个函数所对应的加权因子。
根据实测和计算确定每个函数的变动范围,若已知某项指标的的变动范围为α~β,则该指标所对应函数的加权因子ωj的计算方法为如式(9),其值决定了各单项指标函数的数量级及重要程度。
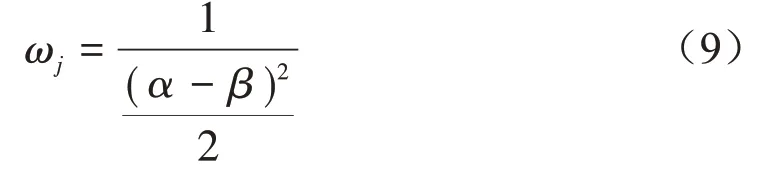
式中α 为5 种过滤器某单项性能指标的最小值,β 为5 种过滤器某单项性能指标的最大值。
参考文献[20]计算得ω1=0.004,ω2=1.2,ω3=0.0007,则综合评价数学模型见式(10)。

将5 种叠片过滤器的d、p、l、fp、θ 以及h 代入式(10)中,得到各叠片过滤器的无量纲综合评价值Q,过滤器I到V 的Q 值依次为7.22、7.08、7.88、8.63、3.11,该值越小,叠片过滤器性能越好。可以看出,过滤器V 的综合评价值较低,过滤器III 和过滤器IV 的综合评价值较高,说明过滤器V 的综合性能较优,而过滤器III、过滤器IV 的综合性能较差。根据表2 和图4 可以看出,单项指标中,过滤器V 和过滤器II 叠片流道沟槽内的泥沙堵塞较为均匀,水力性能较好;过滤器V 和过滤器I 的周期拦沙量较多,过滤器V和过滤器II所拦截泥沙的粒径较小,表现出较优的泥沙处理能力。可见,式(10)可以全面合理地对叠片过滤器性能进行综合评价和对比。
2.4 基于评价公式分析叠片过滤器性能与其结构尺寸间的关系
叠片过滤器的净过流面积指的是叠片沟槽截面的总表面积,代表过流叠片实际使用的面积[21]。叠片的结构尺寸参数决定着净过流面积的大小,而净过流面积的大小又直接影响叠片过滤器的水力性能和对泥沙的处理能力[22-24]。当净过流面积增大时,单位时间系统过流量增多,叠片过滤器的局部水头损失相应降低,但较大的过流面积又会降低滤芯对泥沙的截留能力,小粒径的泥沙不易被截留或容易被挤压带出叠片,过滤器将失去过滤能力。因此,叠片过滤器的性能会根据叠片的结构尺寸参数大小而发生改变[25-26]。
由式(10)可知,当d、θ、h 值越小,或p、l、fp值增大时,指标Q 值都将减小,此时说明叠片过滤器性能优良。而对叠片过滤器进行结构设计时,各参数间的约束性普遍存在,不能通过同时减小d、θ、h 值和增大p、l、fp值来优化其性能。文中叠片过滤器沟槽截面均类似于等腰三角形,因此对于单张叠片来说,其沟槽外截面面积可按式(11)计算。

式中A 为叠片净过流面积,mm2;h 为叠片沟槽外截面三角形高,mm;θ 为叠片沟槽外截面三角形顶角,(°);fp为每片叠片单面沟槽数。
假设叠片外径为R,则叠片沟槽外截面三角形底边长与每片叠片单面沟槽数可按下式计算:

式中R为叠片外径,mm。
假设叠片沟槽能通过的最大泥沙粒径为r,可得如下关系式:
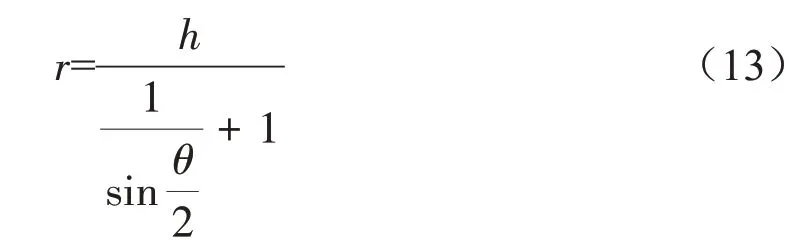
式中r为叠片沟槽外截面三角形内切圆半径,mm。
将式(12)和式(13)代入式(11),可得:

由前文分析可知,叠片过滤器的净过流面积大小影响其水力性能和泥沙处理能力。因此,本文试图通过调整叠片结构尺寸参数来改变叠片过滤器净过流面积与拦截泥沙粒径的相对大小,讨论优化叠片过滤器性能的可能性。
1)保持净过流面积不变,提高泥沙拦截能力
为使叠片过滤器在相同净过流面积下拦截更多的泥沙,应适当减小r 值。由式(14)可知,当r 值减小时,θ 值也相应减小。由式(13)可知,当r与θ值均减小时,h值也需减小。再由式(12)可知,θ与h值减小,fp值必将随之增大。因此,为保证在相同净过流面积下增大其泥沙的拦截能力,对于叠片过滤器设计而言,在叠片结构尺寸上应满足减小θ和h值。同时,fp值也应增大,一般认为更长的沟槽会为更多的泥沙提供沉降空间,这与本文指标Q 的结论相一致。
2)保持拦截泥沙粒径不变,提高水力性能
增大净过流面积能有效的降低叠片过滤器运行过程中的局部水头损失,提高水力性能。因此,保持r 值不变,由式(14)可知,当试图增加叠片过滤器的净过流面积时,θ 值应减小。再由式(13)得,当θ 值减小时,h 值将随之增大,这与上文结论相悖。
一般来说,降低叠片过滤器的局部水头损失与增强其泥沙拦截能力本身就是相对矛盾的。仅仅通过改变θ与h 值的大小,无法综合地满足叠片过滤器对过流能力和泥沙处理能力的要求,其性能的优劣也较难得到评价。而且,当改变h 值后,d 也会随之改变。通过相关分析可知,d 与叠片片数p 之间存在负相关关系(P<0.01)。假设叠片过滤器在额定流量一定的情况下,其滤芯的总高度是固定不变的,若改变d值,p值相应增大或减小,过滤器的性能也会因此受到影响。
因此,d、θ、h、p、l及fp值的增大或减小都会促使综合评价指标Q 值在数值上发生改变。Q 值越小,说明某种过滤器相比于其他过滤器的综合性能更好。此时,综合评价指标能更客观地对比不同叠片过滤器之间在水力性能、泥沙处理能力等方面的综合性能[27-30],但仅通过简单地减小d、θ、h 值,或增加p、l、fp值来降低Q 值并不会同时提高叠片过滤器的水力性能及泥沙处理能力。对于优化叠片过滤器的某项性能参数,更应结合过滤器叠片的几何结构尺寸综合考虑。
3 结论
本文对5 种国内外常见叠片过滤器进行水力性能和过滤性能测试试验,对其单项性能进行比较与分析。试验结果表明:5 种叠片过滤器在拦沙量、拦截泥沙中值粒径、运行周期及堵塞均匀度等方面有较大差异。
在性能测试的基础上,筛选与叠片尺寸参数相关的单项性能指标(拦沙量、拦截泥沙中值粒径、堵塞均匀度),结合线性回归结果,建立基于叠片结构尺寸参数的叠片过滤器性能综合评价的数学模型,并对其进行了理论的分析。5 种叠片过滤器的综合评价结果为:过滤器V(3.11)<过滤器II(7.08)<过滤器I(7.22)<过滤器III(7.88)<过滤器IV(8.63),该指标大小反映出5种叠片过滤器在叠片的结构尺寸上存在差异,从而在堵塞均匀度、周期拦沙量以及拦截泥沙中值粒径等方面表现出差异的现象。
叠片过滤器的结构尺寸参数间存在一定的约束关系,仅通过改变某一参数值的大小很难同时提高过滤器的水力性能及泥沙处理能力。因此,对于优化叠片过滤器的某项性能参数,更应结合过滤器叠片的几何结构尺寸综合考虑。

