台阶溢洪道无因次消能水头规律与水面线计算
王 锦,刘韩生
(西北农林科技大学水利与建筑工程学院,陕西 杨凌 712100)
0 引 言
台阶式溢洪道以高消能率、利于机械化施工、可降低空化空蚀危害等优点成为一种常用的泄流方式,并得到了长足的发展[1- 6]。溢洪道水面线的计算是水力设计的重点,也是确定边墙高度的主要依据。由于台阶结构特殊,台阶式溢洪道水面线的计算方法尚没有系统的研究成果。
张志昌等[7]将台阶式溢洪道视为大粗糙度的常规溢洪道,利用边界层理论来计算台阶式溢洪道的沿程水深;徐啸等[8-9]根据明渠恒定非均匀流理论,推导了台阶式溢洪道未掺气水流水面线的计算;付奎等[10]根据蔡克士大等的明槽试验研究结果,将台阶式溢洪道的台阶视作大粗糙度的渠道,得出了台阶式溢洪道滑行流水深计算公式;文明宜等[11]提出将台阶溢洪道与常规溢洪道的断面比能进行对比,引入相对比能,基于相对比能与流程长度的线性关系,联合常规溢洪道成熟的水面线计算方法,计算台阶溢洪道沿程水面线。
在此基础上,本文从直接反映消能大小的消能水头入手,对台阶式溢洪道的消能水头及影响因素进行因次分析,探究无因次消能水头的规律,通过试验研究发现台阶式溢洪道无因次消能水头与相对位置表现出良好的线性关系,基于这个线性关系,反算台阶式溢洪道的水深。由于消能水头是重要的水力参数,直接反映了台阶式溢洪道的消能量值,消能水头规律对认识台阶式溢洪道至关重要,本文独辟蹊径,依据无因次消能水头规律计算水面线,寻求具有广泛适用性的水面线计算方法。
1 试验概况、消能水头的定义及因次分析
1.1 试验概况
本文进行了5个坡度,3个台阶高度,3个单宽流量下的台阶式溢洪道模型试验,试验工况见表1。

表1 模型试验资料
1.2 消能水头的定义
台阶式溢洪道的消能水头Hw是指水流经过台阶,由于台阶作用消耗的那部分水头,反映的是水流能量的损失值。以台阶式溢洪道末端为基准面,台阶初始位置的总水头,过水断面上的总水头分别为
(1)
(2)
台阶式溢洪道的消能水头为
(3)
式中,H0为台阶式溢洪道初始位置的总水头,m;Z0为台阶式溢洪道上游段相对于基准面的高度,m;h0为上游段水深,m;α0为上游段的动能修正系数;v0为上游段的流速,m/s;g为重力加速度,m/s2;H1为台阶式溢洪道过水断面的总水头,m;Z1为台阶式溢洪道过水断面相对于基准面的高度,m;h1为试验测得的断面平均水深,m;θ为溢洪道坡度,(°);α1为过水断面的动能修正系数;v1为过水断面上的流速,m/s;Hw为台阶式溢洪道的消能水头,m。台阶式溢洪道示意见图1。
1.3 因次分析
对消能水头进行台阶式溢洪道沿程水力参数影响因素的因次分析。影响消能水头的主要因素是单宽流量q,重力加速度g,台阶高度d,流程长度L和坡度θ。函数关系式如下
Hw=f(d,g,q,L,θ)
(4)
式中共有6个物理量,其中自变量有5个。选择d,g两个物理量作为基本物理量,根据量纲和谐原理可得台阶式溢洪道沿程无因次消能水头与相对临界水深hk/d、相对位置L/d、坡度θ有关的函数,即
(5)
2 无因次消能水头的规律
2.1 无因次消能水头与相对位置的关系
不同坡度下,台阶式溢洪道滑行流无因次消能水头与相对位置的关系如图2所示。由图2可以看出,各工况下台阶式溢洪道滑行流整个流段内无因次消能水头沿程表现为较好的线性关系且直线通过原点。无因次消能水头沿程线性关系直线的相关系数见表2,相关系数的最大值为0.999 9,最小值为0.988 3,说明线性关系较好。
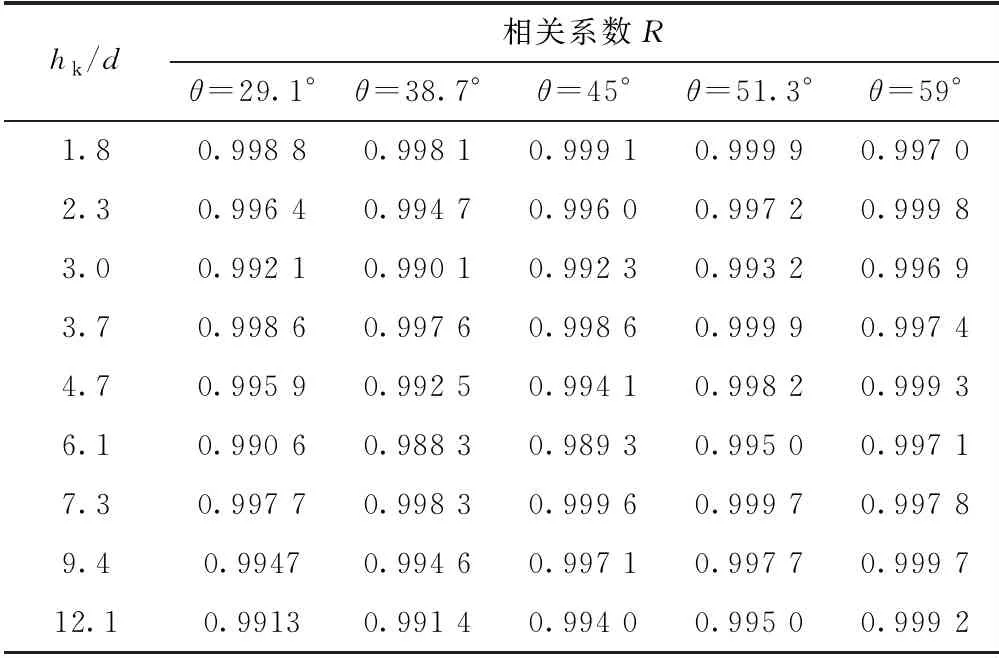
表2 无因次消能水头沿程线性关系相关系数R
鉴于台阶式溢洪道无因次消能水头沿程的线性关系较强,台阶式溢洪道任意位置的无因次消能水头的计算公式可以写为
(6)
式中,k为无因次消能水头沿程线性关系的斜率,它反映了无因次消能水头与相对位置之间的关系,k的影响因素为相对临界水深hk/d、坡度θ。
2.2 斜率变化规律
2.2.1 斜率与相对临界水深的关系
不同相对临界水深下,式(6)中的线性斜率k的值如表3所示,其平均值以及最大差值比较见表4。由表3、表4可知:同一坡度下,随着相对临界水深的增大,斜率k的变化并不明显,与斜率平均值最大差值为0.128。由此可认为,在一定坡度下,不同相对临界水深时无因次消能水头沿程线性关系的斜率为定值,可以用平均值表示这一定值。

表3 不同相对临界水深下的斜率
2.2.2 斜率与坡度的关系
一定相对临界水深下,溢洪道坡度对无因次消能水头线性关系斜率k的影响如图3所示。由图3可以看出,无因次消能水头线性关系的斜率k与溢洪道坡度之间呈不过原点的线性关系,相关系数R为0.977 4~0.990 8,斜率k随坡度的增大而增大,说明坡度增大时台阶式溢洪道无因次消能水头的增长速率随之增大。
2.2.3 斜率与相对临界水深、坡度的关系
为全面分析无因次消能水头的变化规律并给出关系式,图4直观地给出了相对临界水深和溢洪道坡度对无因次消能水头线性关系斜率影响的三维示意。
为了使无因次消能水头线性关系的斜率k的公式具有广泛的适用性,对斜率k进行了多元线性回归, 即
k=-0.1458+1.1901×sinθ-1.12×10-11×hk/d
(7)
式(7)的相关系数为0.987 5,说明公式拟合较好。式(7)的适用范围为:29.1°≤θ≤59°,1.8≤hk/d≤12.1。
3 水面线计算
3.1 无因次消能水头规律计算水面线的方法
首先计算台阶式溢洪道的相对临界水深hk/d,判断是否符合无因次消能水头的斜率经验式(7)的应用条件;如果符合,则根据式(7)计算出无因次消能水头与相对位置线性关系的斜率k;其次按式(6)可计算各断面的无因次消能水头Hw/d,从而得到各断面的消能水头;最后反算出台阶式溢洪道的水面线。
3.2 算例
以坡度38.7°,单宽流量21.96 m2/s,台阶高度0.5 m,流程长度124.86 m为例,计算台阶式溢洪道滑行水流水面线。经计算,hk/d=7.3,符合斜率经验公式(7)的应用条件。
(1)首先根据式(7)计算出斜率k=0.598 3。
(2)将k=0.598 3代入式(6)得到Hw/d。
(3)由无因次消能水头可得各个断面的消能水头,从而计算出台阶式溢洪道的水面线。计算结果见表5。从表5可以看出,计算值与实测值最大误差绝对值不大于16%。
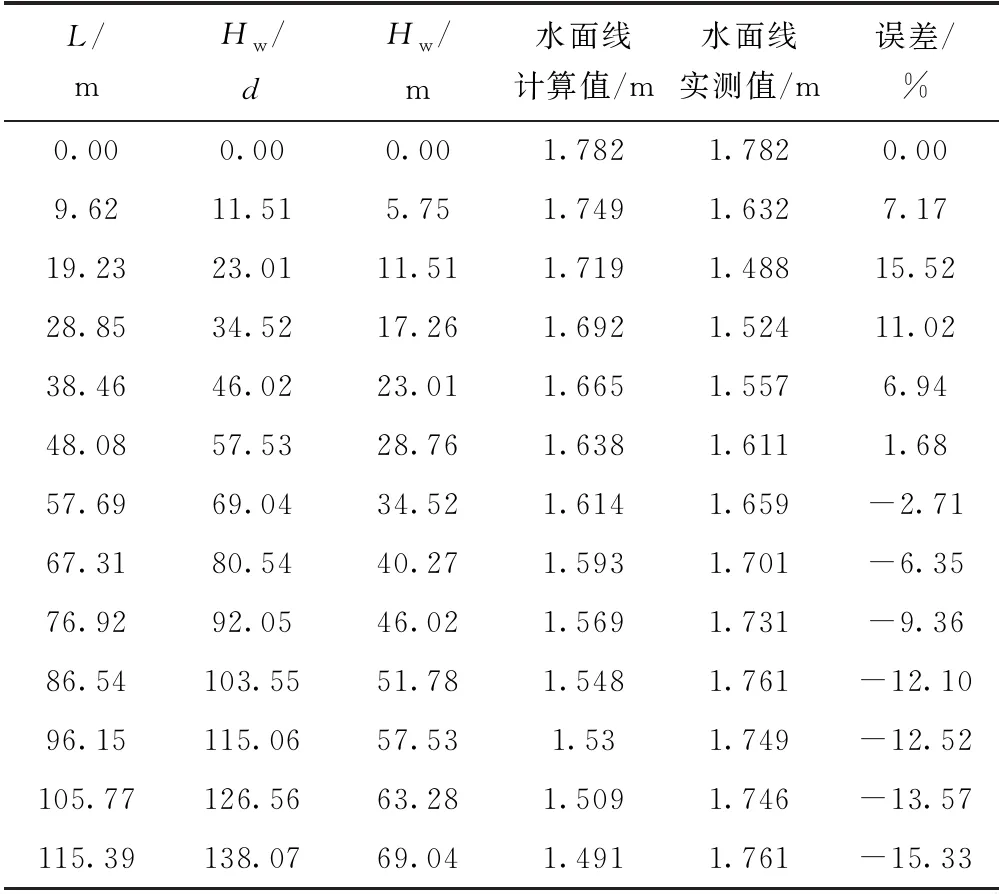
表5 水面线计算结果
4 结 论
因次分析得到无因次消能水头与相对位置、相对临界水深、坡度有关。水力模型试验结果表明,无因次消能水头与相对位置呈良好的线性关系;直线的斜率可认为只与坡度有关,与相对临界水深无关。依据无因次消能水头规律可以计算出台阶式溢洪道的沿程水深,此方法具有较广泛的适用性,可推广应用。

