60°坐标系下三电平感应电机SVPWM算法

北京信息科技大学，北京 100192

一、引言

近年，多电平技术在感应电机矢量控制调速系统得到广泛的应用，其中三电平逆变器SVPWM控制算法成为重点研究对象。传统三电平逆变器控制方法采用基于正交坐标系的SVPWM算法[1]，在参考电压矢量的合成计算时涉及了大量三角函数运算，造成计算机大量运算内存被占用，导致运算效率下降[2]。

本文依据各电压矢量角都是60°的特点，建立新的坐标系，从而缩短矢量合成和作用时间上的运算时间，实现了转速快速控制，最后通过在MATLAB仿真试验平台搭建模型，并使用基于TMS320F2812型DSP运动控制系统实验平台对算法可行性验证。实验结果表明，这种方法避免了大量函数运算，减少了控制系统计算时间。

二、矢量控制系统60°坐标系下SVPWM 算法实现

1、矢量控制

矢量控制将测量得到的感应定子电流经坐标变换，分解为产生磁场的励磁电流分量和产生转矩的转矩电流分量，同时进行幅值和相位控制，即通过控制定子电流矢量，从而达到控制感应电动机转速的目的[3]。

2、坐标变换

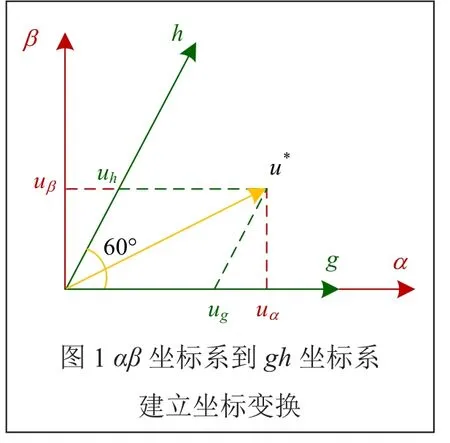
选择g轴与α轴重合，g轴逆时针旋转60°做h轴，建立起60°坐标系，如图1所示。则gh坐标系与αβ坐标系的变换关系为：

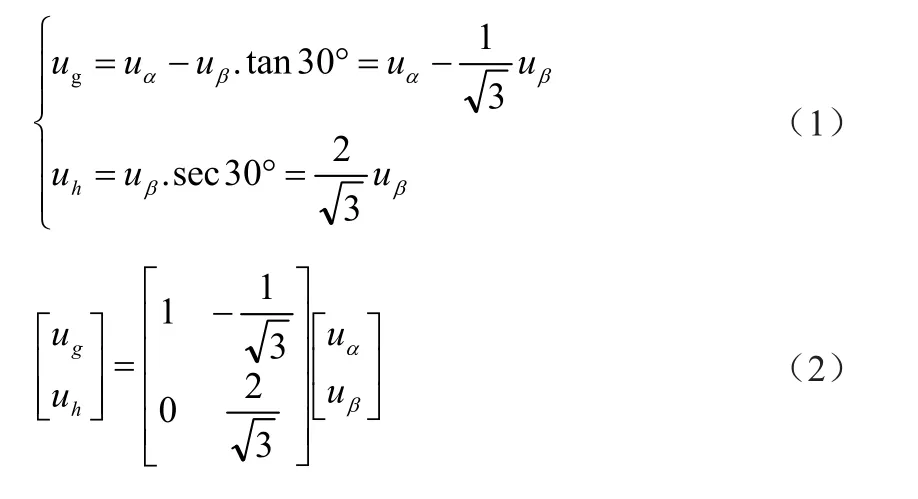
设u为参考电压矢量，三相电压为u(uA uB uC)，(uα、uβ)为αβ坐标轴下的分量，(ug、uh)为变换到gh坐标轴下分量。

通过Clark变换得到gh坐标与ABC坐标的变换关系为：

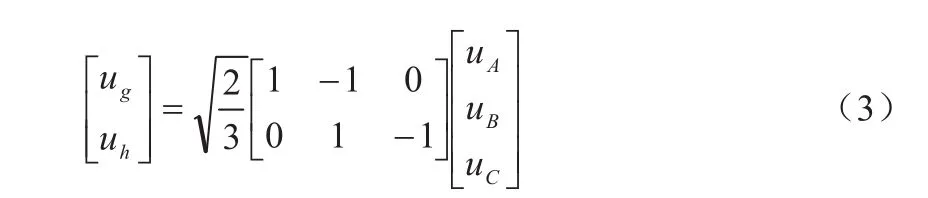
化简后得到：

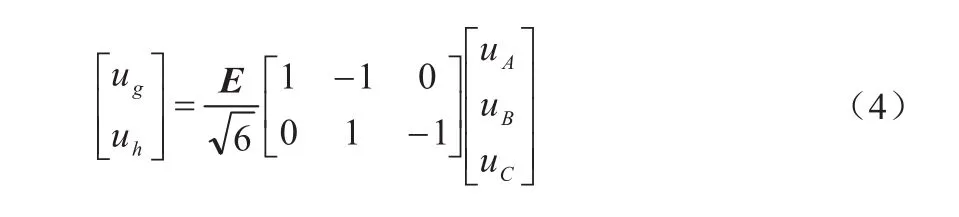
其中，E—单位矩阵。

3、参考电压矢量定位

参考矢量所在的正方形通过取整运算确定[4]。图2中A、B、C、D点为参考矢量N于g、h坐标分别向下取整，所在正方形的4个顶点坐标为：

A点坐标

B点坐标

C点坐标

D点坐标

再确定参考矢量在正方形中所处的三角形区域。当gN+hN≤gB+hB，参考矢量在下半部分三角区域，当gN+hN>gB+hB，则参考矢量位于上半部分三角区域[5]。

4、合成矢量选取及作用时间的计算

以下三角为例，计算合成参考矢量ON的各矢量作用时间，上三角矢量合成类似。

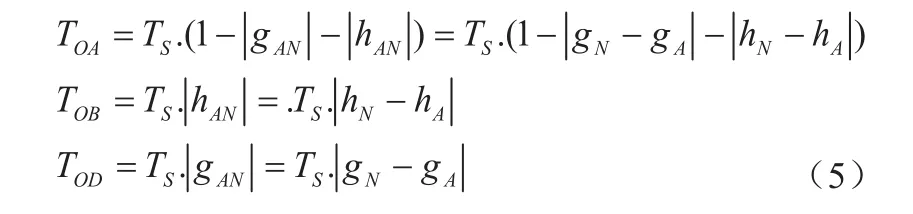
从以上参考矢量扇区的判断和矢量作用时间计算的方法可以看出，与传统算法相类似，但60°坐标系SVPWM 算法在计算难度和复杂度方面都有所降低，若应用于工程，在软件上实现，可提高计算的精确性与实时性[6]。

三、仿真系统设计

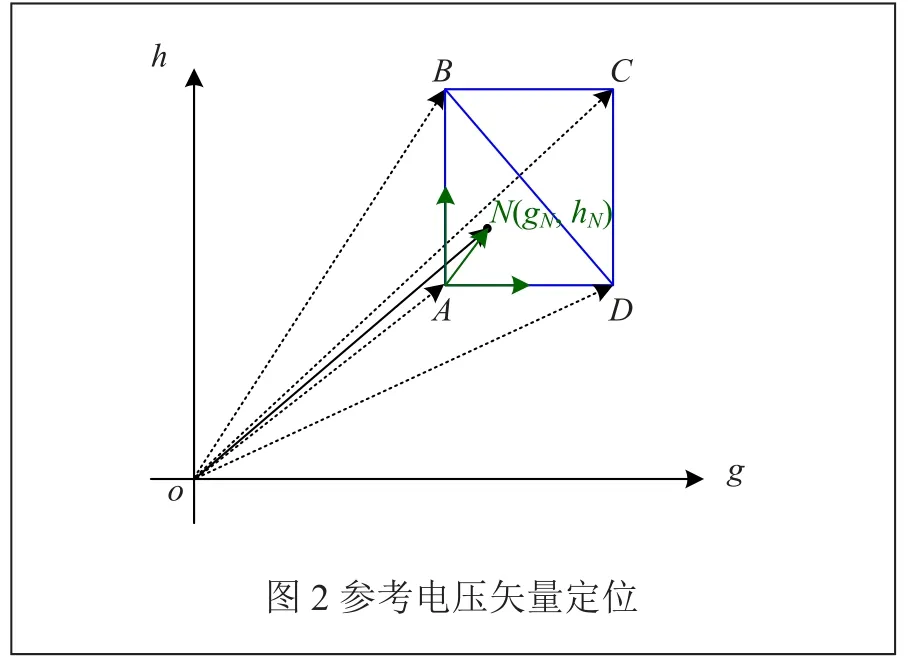
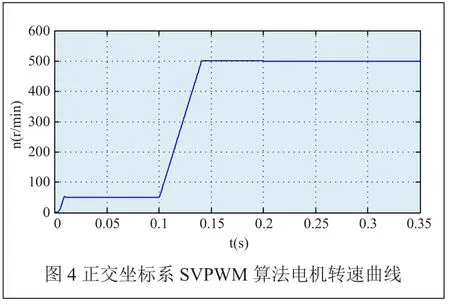
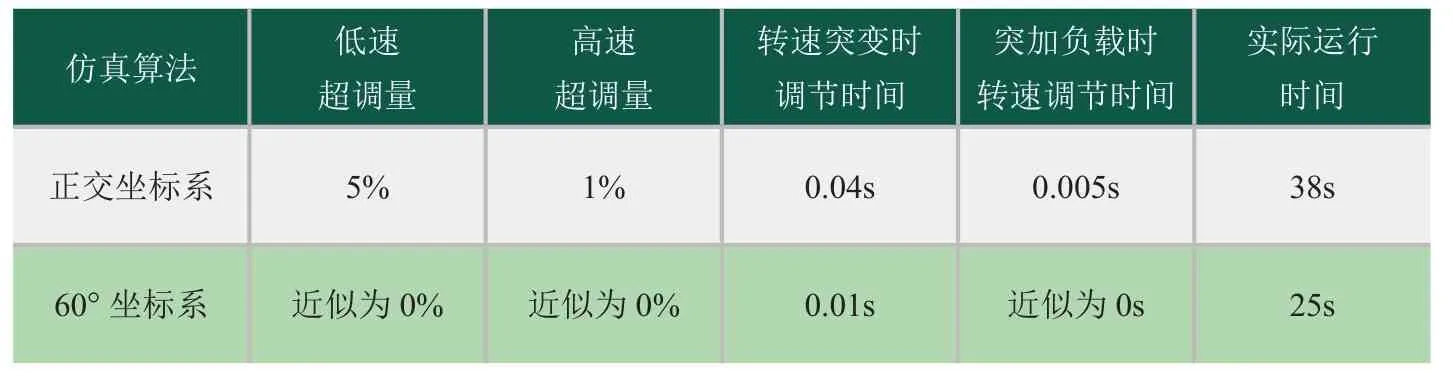
表1 实验数据分析

在Simulink仿真环境下进行验证试验，设定感应电机参数如下：极对数4，定子电阻Rs=4.7Ω，dq轴电感Ld=Lq=L=7.8mH，转子磁动势Ψf=0.215Wb，转动惯量J=0.8×10-4kg·m2。

实验设定系统给定转速在0.5s时从100r/min跳变到600r/min，转矩在0.1s时跳变到10N·m。图4为电机采用正交坐标系下的SVPWM算法获取的转速曲线，图5为电机采用60°坐标系下的SVPWM算法获取的转速曲线。

图4和图5的仿真实验结果，验证了60°坐标系下三电平感应电机SVPWM算法的有效性，在转速和转矩突变时，具有很好的跟踪效果，且在相同的实验条件下与传统SVPWM算法相比，实际运行时间明显缩短。综合上述仿真实验结果表明，采用60°坐标系三电平感应电机SVPWM算法，不仅降低了模型的复杂性，缩短了系统的调节时间，且在稳定时可以达到很高的精度，具有很好的实际应用价值。

四、硬件电路设计

1、硬件平台

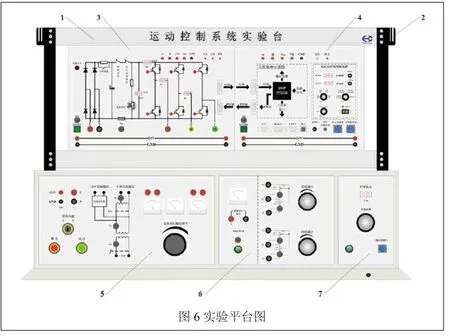
为进一步验证控制策略的有效性，在运动控制系统平台上编写了感应电机转速闭环控制的SVPWM算法程序，并进行调试。电机实验平台被控对象是一台功率为200W的感应电机，实验平台如图6所示。本平台是eMCP1000N运动控制系统实验装置，实验平台所选用的三相感应电机的主要参数包括：额定功率：90W；额定电压：220VAC；额定电流：0.68A；额定转速：1420rpm；额定转矩：0.4N·m；功率因数：0.6；连接方式：角接法。

2、程序设计

主程序主要完成对系统寄存器、时钟、外设接口等的初始化设置，之后对电机转子初始位置进行检测，在得到转子初始位置后，进入中断等待状态[7]。一旦检测到外部产生中断信号时，系统就会进入相应的中断服务子程序对电机进行控制[8]。

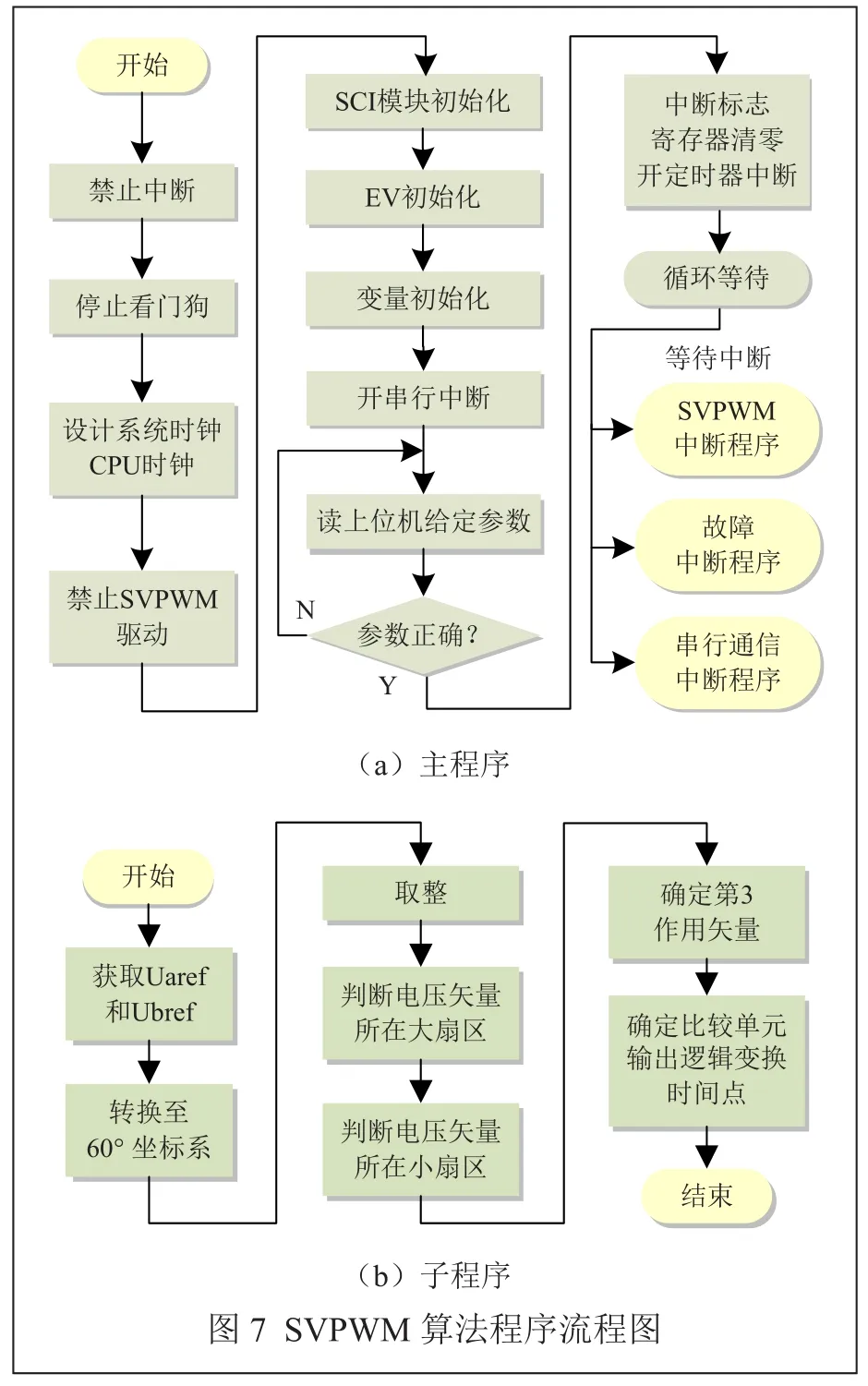
在中断子程序中，启动A/D转换，实现对电流和速度检测，电流检测后进行坐标变换，其中，坐标变换用到的三角函数值通过查表获得[9]。电流反馈值与给定值比较后，偏差通过电流环控制器输出系统所需的电压ud、uq，最终实现SVPWM算法。主程序流程如图7(a)所示，SVPWM算法子程序如图7(b)所示。

五、实验结果

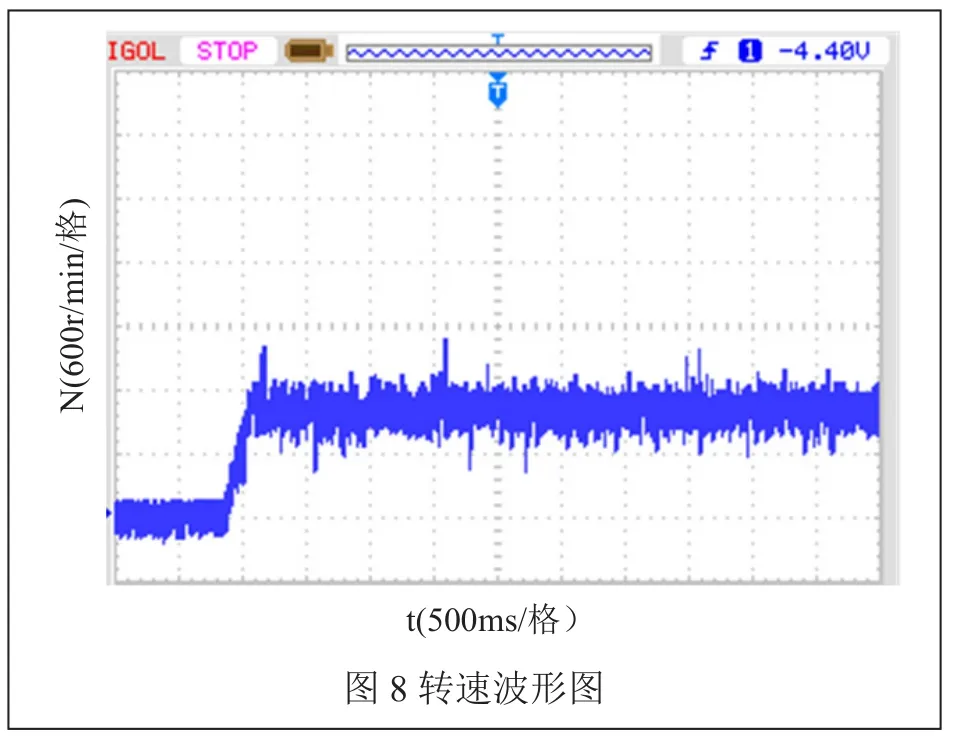
在电机实验平台上，设定电机转速为600r/min，在某一时刻负载转矩从0.06N·m变为0.15N·m时，采用速度闭环控制策略，基于C语言编写算法程序。运用基于正交坐标系下的SVPWM矢量控制算法对交流异步电机进行转速控制实验，图8和图9分别为得到的电机实验曲线结果。

通过图8转速曲线，可以看出程序的有效性。系统在稳定时，转速趋于稳定，说明此算法可以很好地对电机进行控制。图9中检测到的PWM驱动信号上下两路互补。为了使IGBT工作可靠，避免上下桥臂直通，设置了死区时间，因此输出波形并不完全对称。

六、结论

通过上述分析和实验结果验证了基于60°坐标系SVPWM算法的可行性。同时通过多电平逆变器结合60°坐标系SVPWM算法与感应电动机调速系统进行组合应用，一方面简化了计算步骤，另一方面还提高了计算准确度，满足了工程需要。该算法能为电机的控制算法提供新的思路，满足实际控制系统需求。