基于自适应准谐振控制的DFIG-GSC次同步振荡抑制策略研究
孙东阳,申文强,孟繁易,沙昱彤,王南,胡博
(1.哈尔滨理工大学 电气与电子工程学院,黑龙江 哈尔滨 150080;2.哈尔滨工业大学 电气工程及其自动化学院,黑龙江 哈尔滨 150001;3.国家电网辽宁省电力有限公司,辽宁 沈阳 112000)
0 引 言
随着现代电力系统的发展,风能等新能源在电力系统中的占比不断增加。电力系统常采用串联补偿电容的方式来提升线路的输电能力,但这加剧了系统产生次同步振荡(sub-synchronous oscillation,SSO)的风险[1-3]。双馈感应发电机(doubly-fed induction generator,DFIG)动态调节灵活、风电转化率高,是一种常用的风力发电机,其网侧变流器(grid-side converter,GSC)与电网直接相连。在电网SSO状态下,GSC侧的直流母线电压会产生相应的振荡分量,影响转子侧变流器(rotor-side converter,RSC)的控制,危害DFIG的稳定运行[4-5]。SSO会使得DFIG输出功率振荡,对相连线路产生影响,严重则会导致风机脱网,火电等发电机组切机事故[6-8]。2012年以来,我国河北沽源地区双馈风电场发生了多起因线路串补度较高引起的次同步振荡事故,造成风电机组因谐波过大被迫切机弃风,导致风能的浪费[9-10]。2015年,新疆哈密风电场出现SSO,振荡扩散到整个哈密电网,导致300 km外的火电机组被迫切机[11]。因此,研究DFIG并网系统的SSO抑制具有重要的工程意义。
针对DFIG系统SSO的抑制措施有多种,常见的振荡抑制措施有切除风机及无功负荷、增加虚拟电阻[12]。这些方法实施难度低,抑制响应迅速,但是存在设备成本高、控制灵活性低等问题。改进变流器的控制策略也是实现SSO抑制的重要手段,文献[13-14]提出在DFIG变流器中采用附加阻尼控制,提升系统阻尼来抑制电网SSO对GSC的影响。这种抑制措施较为传统,一般只能消除特定频率的振荡。文献[15]利用比例谐振(proportion resonant,PR)控制器对交流信号的追踪能力,在GSC侧采用PR控制器来抑制直流母线电压和网侧无功功率的振荡,在RSC侧采用PR控制器来抑制定子电流振荡,并在固定频率下验证该控制策略的性能,但未考虑SSO频率变化的情况。
针对电网SSO对DFIG直流母线电压产生扰动的问题,本文提出一种基于自适应准谐振控制的DFIG-GSC次同步振荡抑制策略。首先,建立电网SSO状态下GSC的数学模型,推导出在电网存在SSO时,直流母线电压中的振荡分量。其次,提出借助准谐振控制器对交流信号的追踪特性来抑制直流母线电压的振荡,并采用递归思路设计GSC反步控制器,提升GSC系统的抗干扰性。此外,针对频率变化的电网SSO,采用自适应准谐振控制器来抑制频率变化的电网SSO时直流母线电压的振荡。最后,搭建DFIG系统实验平台,验证所提SSO抑制策略的有效性。
1 电网SSO影响下GSC数学模型的建立
GSC的主要控制目标是维持直流母线电压的稳定[16]。为了分析电网SSO下的直流母线电压状态,需要建立电网SSO情况下的GSC数学模型,电网SSO下的GSC拓扑如图1所示。图中:uga0、ugb0、ugc0与iga0、igb0、igc0分别表示电网理想情况下的三相电压与电流;uga_sub、ugb_sub、ugc_sub与iga_sub、igb_sub、igc_sub分别表示电网次同步电压与次同步电流分量;R与L分别表示线路电阻与电感值;C为直流母线侧电容;Udc表示电容电压值;iLoad为负载电流。
电网SSO下,网侧电压表达式为:
(1)
此时,网侧电流表达式为:
(2)
由图1所示的GSC电路拓扑,可以得到:
(3)
式中:vao、vbo、vco分别为GSC三相桥臂相电压;sa、sb、sc分别为开关函数,其值为0或1。
将式(1)~式(2)代入式(3)中,同时进行Park变换得到电网SSO下GSC的d-q轴数学模型为:
(4)
式中:ugd=ugd0+ugd_sub;ugq=ugq0+ugq_sub;igd=igd0+igd_sub;igq=igq0+igq_sub;Udc=Udc0+Udc_sub。ugd0、ugq0与igd0、igq0为网侧电压、电流在d-q坐标系下的基波值;ugd_sub、ugq_sub与igd_sub、igq_sub为网侧电压、电流在d-q坐标系下SSO分量值;Udc0为理想电网下直流母线电压稳态值;Udc_sub为电网SSO下直流母线电压振荡值;ω1为理想电网电压矢量角频率;vdo、vqo为GSC桥臂相电压在d-q坐标系下的值;sd、sq为d-q坐标系下的开关函数。
由式(4)可知,在电网SSO的情况下,Udc也包含振荡分量,其与网侧SSO电流的关系为
(5)
对式(5)积分,可得到Udc_sub的表达式为
Asin[(ωn-ω1)t+
(6)
式中:A为Udc_sub的幅值,其值由电网SSO以及线路参数共同决定;φi_sub为网侧次同步电流的初相角;φ1则为网侧基波电流的初相角。由式(6)可知,当电网出现频率为ωn次同步电压时,Udc将会产生一个频率为ω1-ωn的振荡分量。
为了研究电网SSO对DFIG的影响,对SSO下的DFIG进行仿真分析。考虑到DFIG稳定运行时,Udc和转子电流在d-q坐标系下的分量均为稳定的直流量,因此选择Udc、ird和irq作为观测目标。仿真结果如图2所示。
图2为电网SSO频率分别为10 Hz与20 Hz,且SSO电压幅值为电网基波电压幅值的20%时,Udc与ird、irq的波形图。由图可知,当电网存在10 Hz的SSO时,Udc的振荡频率为40 Hz;当电网存在20 Hz的SSO时,Udc的振荡频率为30 Hz;同时,Udc振荡会致使转子电流产生畸变,进而影响RSC的正常工作。因此,需要设计相应的SSO抑制策略以维持Udc稳定。
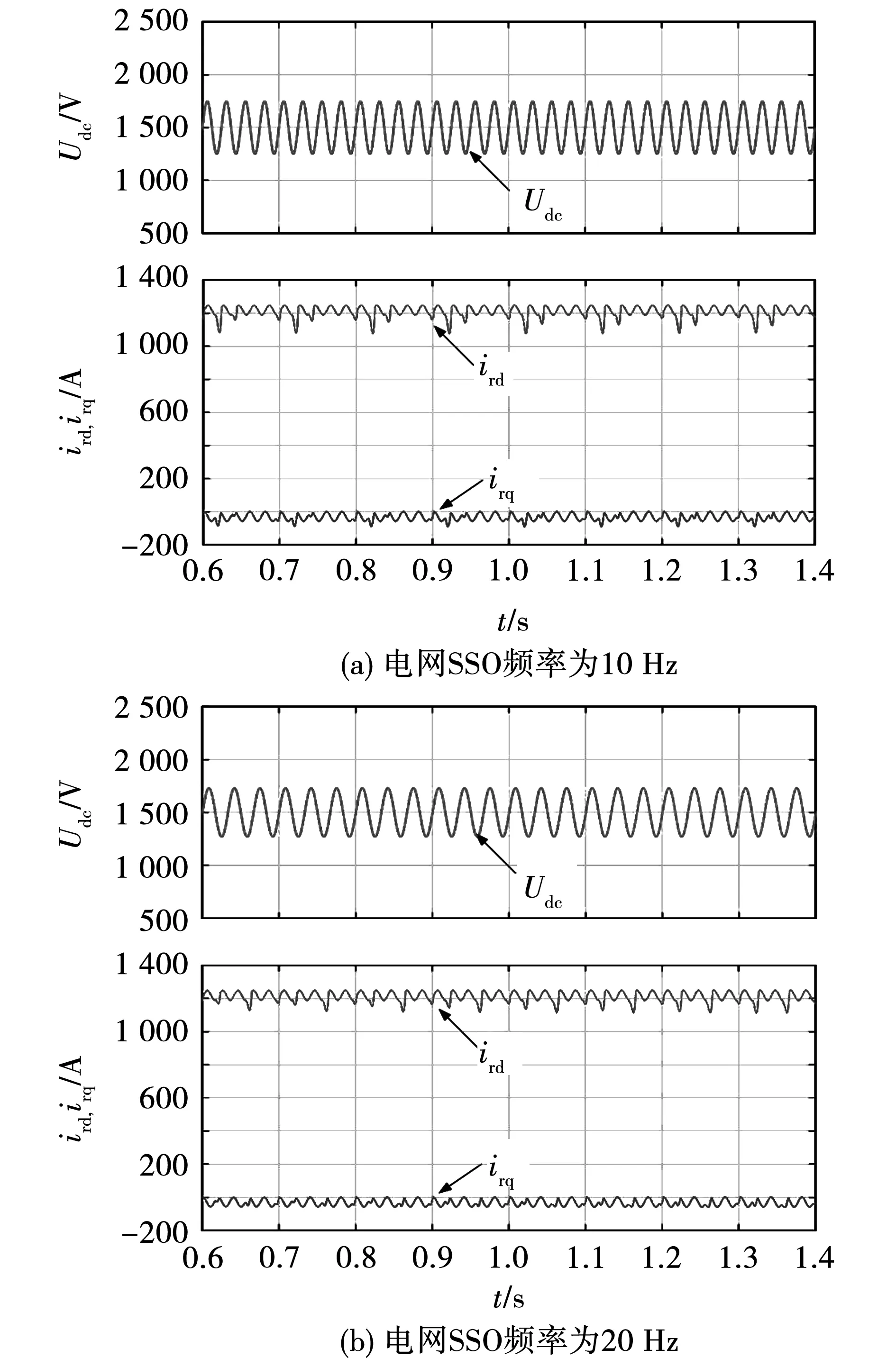
图2 SSO下的直流母线电压与转子电流波形图Fig.2 Waveforms of Udc and rotor current under SSO
2 GSC次同步振荡抑制机理
通过建立电网SSO作用下的GSC数学模型可知,电网SSO会使得Udc产生交流振荡。故本文利用准谐振控制器对交流信号的追踪特性对输入到GSC的振荡进行抑制,并针对变频率的电网SSO,利用自适应准谐振控制器进行追踪抑制;同时,采用递归设计思想构造反步控制器进一步提高GSC系统的鲁棒性。
2.1 准谐振控制器
准谐振控制器传递函数[17-18]为
(7)
式中:KR为谐振控制器的增益系数;ωb为谐振带宽;ω0为谐振频率。
采用Bode图对式(7)所示的准谐振控制器进行分析。设ω0为314 rad/s,分别改变KR与ωb时,谐振控制器的控制性能变化如图3和图4所示。

图3 KR变化时G(s)的Bode图Fig.3 Bode diagram of G(s) as KR changes

图4 ωb变化时G(s)的Bode图Fig.4 Bode diagram of G(s) as ωb changes
由图3可知,当准谐振控制器的ωb固定时,其幅值增益与KR大小呈正相关;由图4可知,当KR固定时,其幅值和相位随着ωb的增大而趋于平缓。同时可以明确,无论KR与ωb如何改变,准谐振控制器对于频率为ω0的信号追踪效果最好。
但是,当电网SSO频率变化时,Udc将会随着电网SSO的频率实时变化,这时准谐振控制器由于谐振频率固定就难以追踪Udc中的次同步振荡分量,故需要采用自适应算法来实现谐振频率的变化。
2.2 基于GSC数学模型的反步控制设计
反步设计法主要思想是通过构造闭环系统的Lyapunov函数来获得反馈控制器,提升闭环系统的稳定性[19-20]。考虑电机控制过程中所存在的噪声信号,设计相应的反步控制器可以提高GSC系统的抗干扰能力。
采用电网电压d轴定向,对式(3)进行整理可得:
(8)
采用反步法设计控制器时,首先需要根据GSC电压外环设计反步追踪误差e1,并且设计Lyapunov函数为:
(9)
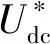
为了保证控制系统能够稳定收敛,需要令Lyapunov函数导数变化为
(10)
式中k1为Lyapunov导数系数,此时令
(11)
根据式(9)~式(11),可以得到
(12)
将式(12)代入式(8)中可得
(13)
根据GSC电路拓扑,有
iLoad=igd+igq。
(14)
将式(14)代入式(13)可得
(15)
经过整理可得
(16)
其中令:
(17)
接下来设计内环的反步控制器。首先建立相应的反步追踪误差,并且设计Lyapunov函数为:
(18)
Lyapunov函数导数设计为
(19)
式中k2、k3为Lyapunov导数系数,此时有:
(20)
将式(20)代入式(8)可得:
(21)
对式(21)进行整理可得:
(22)
其中令:
(23)
由于DFIG在运行的过程中存在噪声信号,对于GSC控制策略会产生不利影响。因此,本文设计了反步控制器提高GSC控制系统的鲁棒性。
3 SSO频率变化下直流母线电压抑制策略研究
3.1 GSC自适应准谐振控制器与反步控制器设计
由2.1节分析可知,考虑到电网SSO频率变化的情况,所设计的准谐振控制器需要具有变频率SSO追踪的功能。
将式(7)进行整理可得
(24)
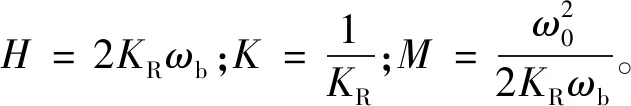
此时,设谐振控制器输入信号为vin=Asin(ω0t)。为了实现对vin的频率追踪,则根据式(24),由vin的频率ω0可以得出此时谐振控制器的频率控制参数M为
(25)
则谐振控制器输出vout表示为
vout=A|G(jω)|sin(ω0t+∠G(jω))。
(26)
式中:
根据图3~图4以及式(26)可知,当谐振控制器中ω0为确定值时,若输入信号频率为ω0,此时谐振控制器的输出与输入信号保持同频同相。式(25)则表明,参数M与ω0呈现正相关性。当vin频率发生变化时,vin与vout在以vout过零点为中心的小范围内可近似表现为线性关系。vin与vout的误差信号则表明了频率控制参数M的调节方向。因此可以通过vin与vout的误差信号对M进行实时调节,从而达到准谐振控制器频率自适应的控制要求。根据式(24)设计自适应准谐振控制器如图5所示[21]。
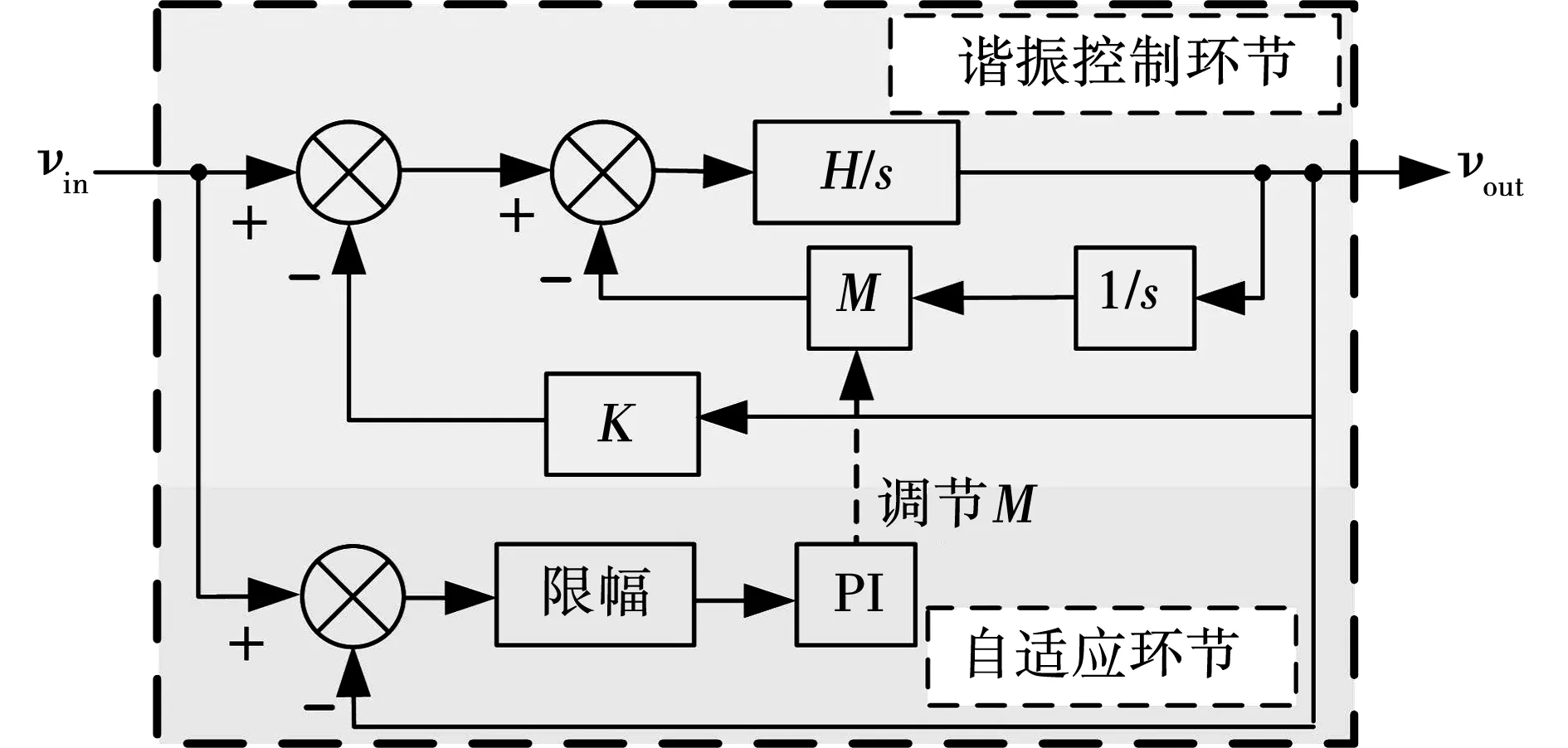
图5 自适应准谐振控制器框图Fig.5 Adaptive quasi-resonant controller block diagram
图5中自适应准谐振控制器可以分为两部分,分别为自适应环节与谐振控制环节。由图可知,当输入信号vin的频率增加或减小时,控制器参数M也需要随之变化,从而使得输出信号同频同相,二者间的相位差也趋近于0,最终达到对输入信号的完全追踪。
根据图5搭建自适应准谐振控制器仿真模型,设K=1、H=100,初始谐振频率ω0为10 Hz。自适应准谐振控制器控制效果如图6所示。图中,原输入电压幅值为10 V、频率为10 Hz,在0.5 s时输入电压幅值、频率、相位均发生变化。此时,自适应准谐振控制器的参数M将发生改变,完成对变频率、幅值、相位的输入电压信号追踪。

图6 输入信号变化时的自适应准谐振控制器效果图Fig.6 Effect diagram of the adaptive quasi-resonant controller when the input signal changes
本文中GSC控制目标为维持Udc恒定和控制变流器功率因数为1,因此,自适应准谐振控制器的输入量应为直流母线电压与网侧无功功率,控制器输出量则为直流母线电压与网侧无功功率中次同步分量的控制指令。
同时,基于反步法,根据GSC系统的数学模型设计GSC反步控制策略,如图7所示。
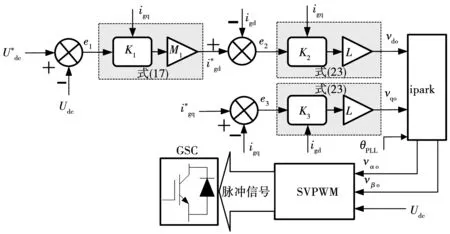
图7 GSC反步控制策略Fig.7 GSC backstepping control strategy
图7中采用反步控制器代替PI控制器,电压外环与电流内环控制器分别按照式(17)和式(23)设计。GSC控制策略分别采用反步控制器与PI控制器时Udc的效果如图8所示。
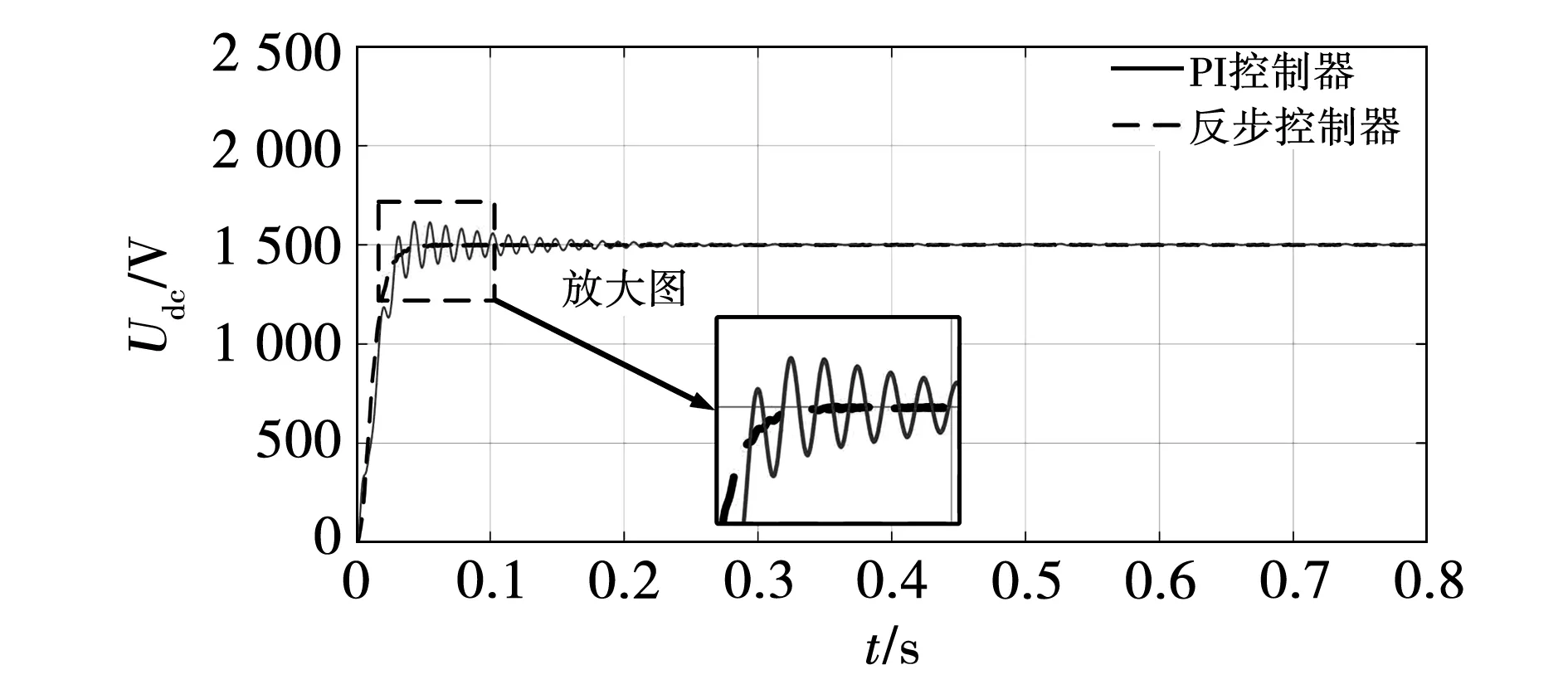
图8 采用不同控制器时直流母线电压波形图Fig.8 Based on Udc waveforms with different controllers
由图8可知,两种控制方案均能控制Udc达到期望值。但是由于噪声信号的干扰,PI控制器的效果并没有像反步控制器一样快速且无超调地追踪上Udc参考值。由此可见,反步控制器受到噪声信号这类小扰动的干扰较小,能够更快地收敛于期望值,提高GSC系统的稳定性。
3.2 GSC侧SSO抑制策略设计
通过建立电网SSO下GSC数学模型可知,在电网SSO情况下,GSC控制目标中分别含有基波分量与次同步分量。针对不同分量,本文提出通过反步控制器控制基波分量,自适应准谐振控制器控制次同步分量,由此设计的SSO抑制策略如图9所示。
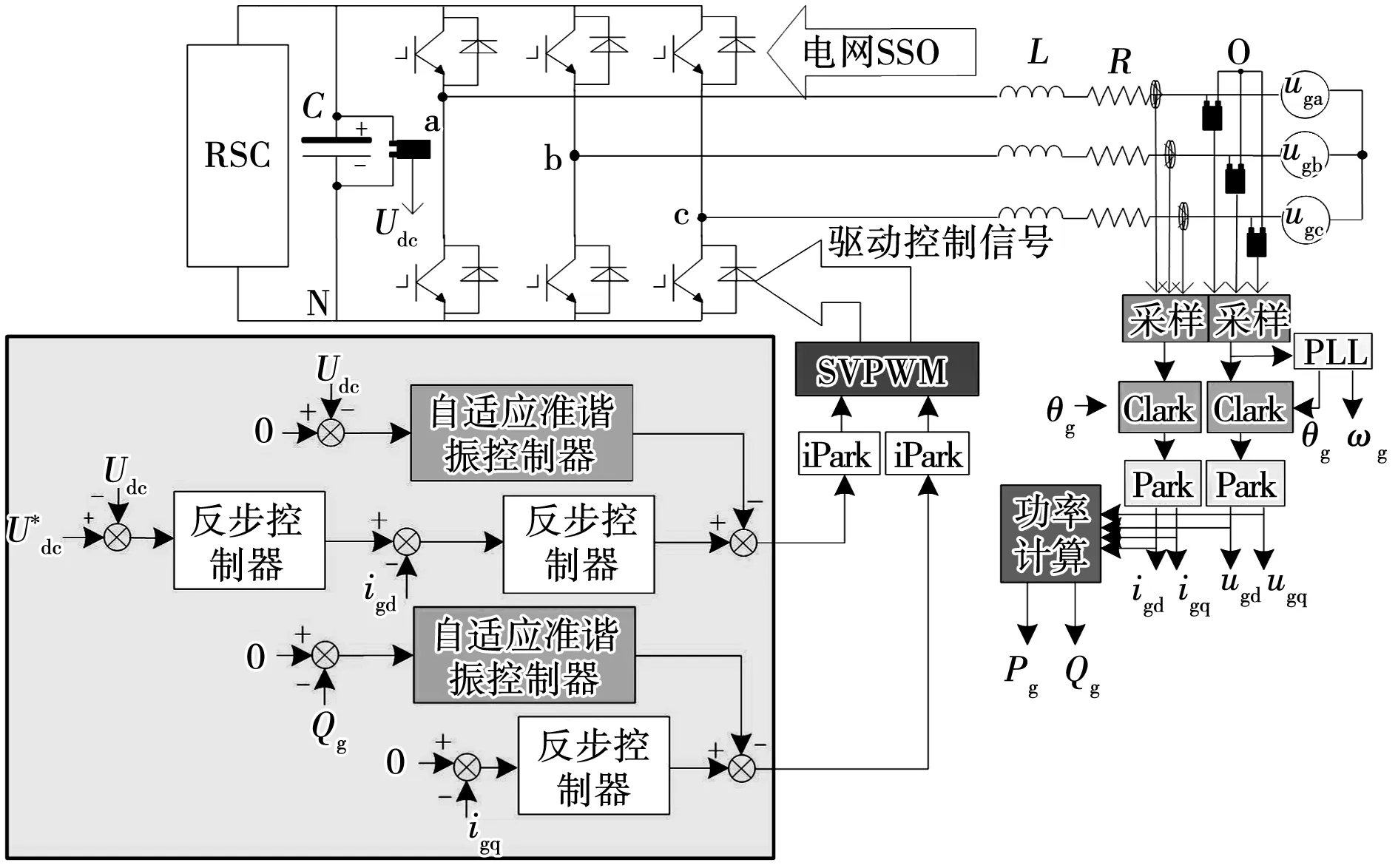
图9 基于反步-自适应准谐振控制器的SSO抑制策略Fig.9 SSO suppression strategy based on backstepping-adaptive quasi resonant controller
在电网无SSO分量时,GSC控制系统无振荡分量。GSC控制目标为维持Udc恒定以及控制GSC的功率因数为1。Udc的恒定由电压外环实现;GSC功率因数为1通过控制Qg为0来实现。由前述分析可知,通过所设计的反步控制器便能实现GSC的控制目标。在该过程中,反步控制器可以减少基波分量中噪声信号的干扰,并且增加系统响应速度,提高稳态精度。
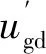
通过上述分析可知,反步控制器用于控制Udc和Qg中的基波分量,自适应准谐振控制器则用于控制Udc和Qg中的次同步分量。二者共同作用保证了在电网SSO发生时,GSC不受振荡的干扰,维持Udc和Qg的稳定,确保GSC控制目标的实现。
4 实验验证
为了验证所提抑制策略的实际效果,本文以15 kW的DFIG为例,对所提抑制策略进行验证。实验平台如图10所示。

图10 DFIG系统实验平台Fig.10 DFIG system experimental platform
图10中,DFIG实验平台主要由GSC、RSC、模拟电网、模拟风机、模拟SSO发电系统以及DFIG等单元构成。实验平台参数如表1所示。
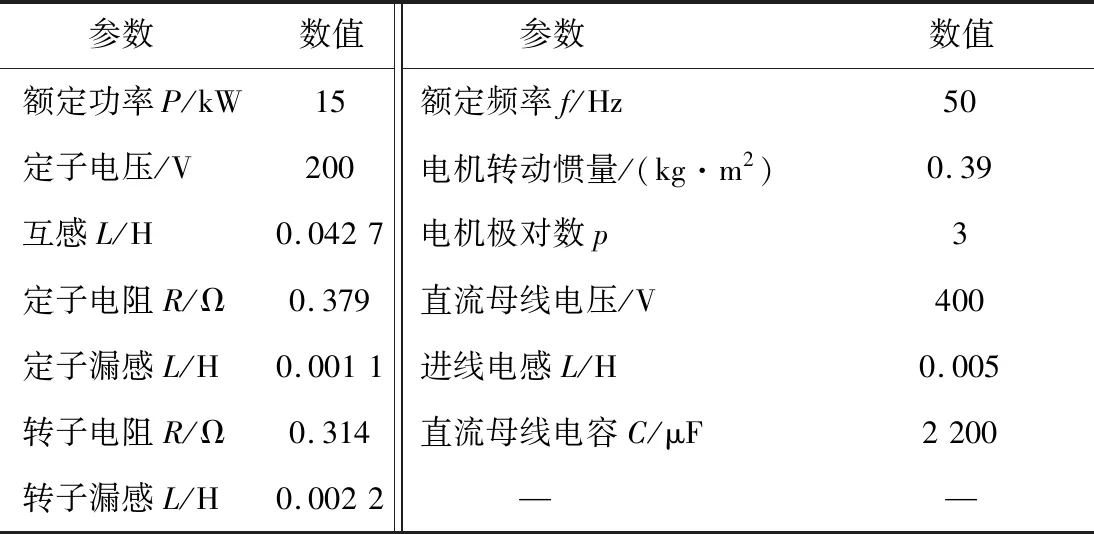
表1 DFIG实验平台相关参数Table 1 DFIG experimental platform related parameters
实验前,要确认是否满足并网条件,电网A相电压与并网前DFIG的A相电压波形如图11所示。
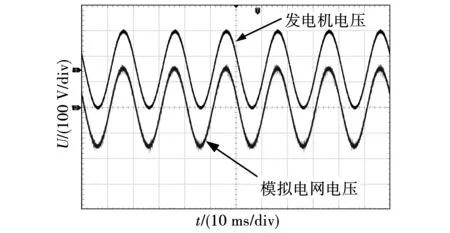
图11 电网与并网前DFIG输出电压波形Fig.11 Power grid and DFIG output voltage waveform before grid connection
图11中,电机定子A相电压与电网A相电压幅值、频率、相位一致,满足并网条件。满足并网条件后,需要验证SSO模拟电机是否顺利投入到电网中,SSO模拟电压并网波形如图12所示。

图12 投入SSO下电网电压波形Fig.12 Grid voltage waveform under SSO
图12中,在T1时刻,投入SSO的频率为10 Hz,幅值为理想电网电压的20%,图12的电网电压表明,SSO模拟电机在T1时,顺利并入到电网中。
下面验证所提抑制策略的有效性,转子转速固定为900 r/min,SSO电压的幅值为理想电网电压的20%,频率分别为10与20 Hz。通过采样电路获得转子转速、A相电网电压、模拟振荡电压、Udc以及Qg的值,实验结果如图13~图14所示。

图13 电网SSO频率为10 Hz时的振荡抑制对比波形Fig.13 Oscillation suppression comparison waveform when the SSO frequency of the power grid is 10 Hz
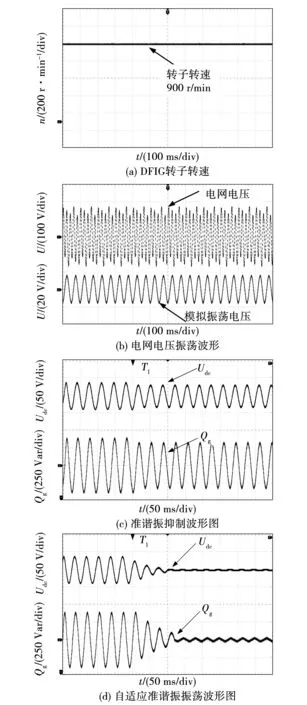
图14 电网SSO频率为20 Hz时的振荡抑制对比波形Fig.14 Oscillation suppression comparison waveform when the SSO frequency of the power grid is 20 Hz
图13~图14中,准谐振控制器的谐振频率均为40 Hz。对比实验结果可知,当电网SSO产生时,Udc和Qg均会产生振荡。在采用谐振控制器抑制后,图13中Udc和Qg振荡明显降低,但图14中的Udc和Qg几乎不变;而在采用自适应准谐振控制器抑制后,图13~图14中的Udc和Qg均有明显降低。
上述实验验证了本文所提抑制策略可以保证Udc和Qg在不同SSO频率下的稳定,但是还需要进一步观察采用该策略后,GSC网侧电流的畸变情况。实验及结果如图15~图16所示。

图15 电网SSO频率为10 Hz时GSC网侧电流波形Fig.15 Current waveform of GSC grid side when grid SSO frequency is 10 Hz
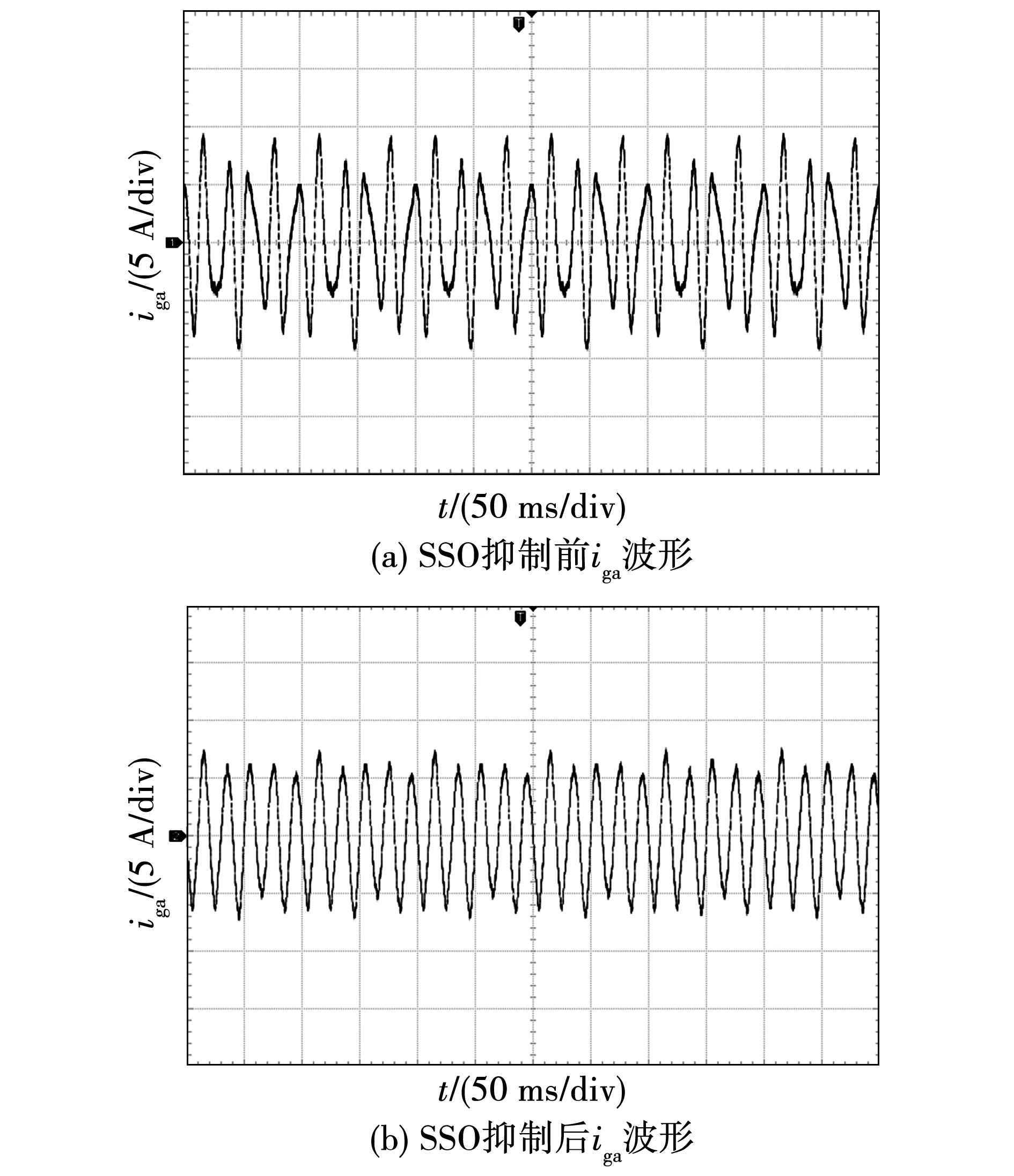
图16 电网SSO频率为20 Hz时GSC网侧电流波形Fig.16 Current waveform of GSC grid side when grid SSO frequency is 20 Hz
图15~图16分别为电网SSO频率为10与20 Hz时DFIG网侧a相电流波形。可以看出,当电网存在SSO时,网侧电流含有次同步分量,输出电流波形存在明显畸变。采用自适应准谐振控制后,网侧电流中的次同步分量被明显削弱。
最后,对准谐振控制器与自适应准谐振控制器在SSO频率突变时的Udc振荡抑制效果进行实验分析,实验结果如图17所示。

图17 电网SSO频率突变时的Udc振荡抑制对比波形Fig.17 Udc oscillation in the grid SSO frequency mutation
图17中,SSO电压的初始频率为10 Hz,振荡幅值为电网基波电压幅值的20%。在T0时刻分别投入准谐振控制器与自适应准谐振控制器进行控制。通过观察Udc波形可知,在投入2种控制器后,Udc中的振荡分量被明显削弱,2种控制器对10 Hz的SSO均能起到抑制效果。在T1时刻,SSO频率突变为20 Hz,振荡幅值不发生改变。振荡频率突变超出谐振控制器的控制范围,在T1时刻后Udc电压出现相应的30 Hz振荡分量;但自适应准谐振控制器在振荡频率突变后,仍能实现对SSO分量的控制,在电网SSO频率突变约0.1 s后,Udc恢复平稳。
5 结 论
针对电网SSO影响直流母线电压稳定性的问题,同时考虑电网SSO频率变化对振荡抑制策略的影响,本文提出一种基于自适应准谐振控制的DFIG-GSC次同步振荡抑制策略。由实验结果得出以下结论:
1)采用准谐振控制器控制能够显著地抑制直流母线以及网侧无功功率中的振荡分量,但因为其谐振带宽有限,并不能够对变频率的SSO起到很好的抑制效果。因此,本文针对电网SSO频率变化情况,提出采用自适应准谐振控制器抑制直流母线电压与网侧无功功率中的振荡分量。通过实验对比分析,自适应准谐振控制器可以抑制宽频率范围内的直流母线电压以及网侧无功功率的振荡,且在振荡频率突变的情况下仍能快速响应,实现GSC的控制目标。
2)基于李雅普诺夫稳定性定理设计的GSC反步控制器控制效果要明显优于PI控制器,当存在噪声等外部干扰时,能够迅速实现直流母线电压的稳定,提升GSC系统的鲁棒性。
综上所述,本文通过实验验证了所提SSO抑制策略的有效性。采用该策略可以提高GSC的抗干扰能力,维持直流母线电压的稳定,为DFIG系统的稳定运行提供保障,具有一定的工程价值。

