基于改进Hilbert-Huang变换的交叉互联电缆在线故障定位策略研究

马驰，李江涛

(西安交通大学 电力设备电气绝缘国家重点实验室，陕西 西安 710049)

0 引 言

随着我国城市化进程的加快和经济规模的扩大，我国的城市用电量呈现激增趋势。电力电缆的使用既满足了城市电网大容量电能传输的要求，又避免了对城市面貌的破坏[1]。电缆的安全可靠运行对城市电网的稳定起着至关重要的作用[2]。高压电缆护层接地方式主要包括单端接地、两端接地、交叉互联接地等。交叉互联接地方式利用高压电缆三相护层换位连接的方式削弱护层上的感应总电压，从而有效抑制护层上的感应电流，因此被广泛应用于长距离电缆输电系统中[1]。但是，交叉互联电缆复杂的连接方式也给相应的故障定位方法提出了新的要求和挑战。

目前比较常用的电缆故障定位方法可以分为在线方法和离线方法两类。电桥法和声磁法[3]等离线方法技术较为成熟，但是存在停电时间较长且需要解开电缆终端及交叉互联结构等缺陷[4]。在线方法主要包括阻抗法和行波法[5]，阻抗法是通过测量和计算故障点到测量端的阻抗，然后根据线路参数列写求解故障点方程，从而求得故障距离[6]。阻抗法虽然简单但是误差较大，并不适用于连接较为复杂的交叉互联电缆系统。行波法是通过识别一个或多个故障波到达的时域信号，根据提取的信息估计故障位置[7]。

近年来，许多学者利用小波变换对故障定位问题进行研究[8-10]。小波变换能够根据故障定位终端记录的信号自动确定故障位置，从而减少对相关技术人员的需求。但是，小波变换需要选择特性的小波基函数及尺度，同一电缆线路使用不同小波基函数进行定位的差别可能较大，不同电缆线路合适的小波基函数不尽相同，这就意味着小波变换的自适应性较差，给电缆系统的自动化定位带来了局限性。

大多数在线故障定位方法是针对架空线路输电系统和配电系统开发的，而与交叉互联电缆故障定位直接相关的文献很少。本文通过建立交叉互联电缆的暂态仿真模型，研究不同模式波在交叉互联电缆系统中的传播特性，提出以双端法识别同轴波到达时刻的故障定位方法；提出使用改进Hilbert-Huang变换及权信号强度判据的在线故障定位策略，能够克服传统小波变换方法不具有自适应性的弊端；最后，结合具体案例对该在线故障定位策略进行仿真验证，结果表明该在线定位策略具有良好的精度。

1 基于行波法的交叉互联电缆故障定位理论

1.1 行波故障定位方法

当电缆系统发生故障时，瞬态电压和电流波将从故障位置沿两个方向向电缆连接的端子传播[11]。利用行波法对电缆故障进行定位的基本思想是识别一个或多个故障波到达的时域信号，并根据提取的信息估计故障位置[7]。

行波法可分为单端法和双端法。单端法仅需设置一个故障定位终端(fault location terminal,FLT)，依据故障定位终端检测到的某种模式下第一波及第二波的到达时间即可推算故障发生的位置[12]。对于直连互联电缆，行波仅会在端子处发生折反射，使用单端法较为有效；但是，对于交叉互联电缆，特别是小段长度不相等的交叉互联电缆，由于交叉连接处阻抗存在不连续性，故波在传播过程中存在大量的折反射，如图1所示，这将导致对固定模式下第二波的检测变得难以实现[12]。

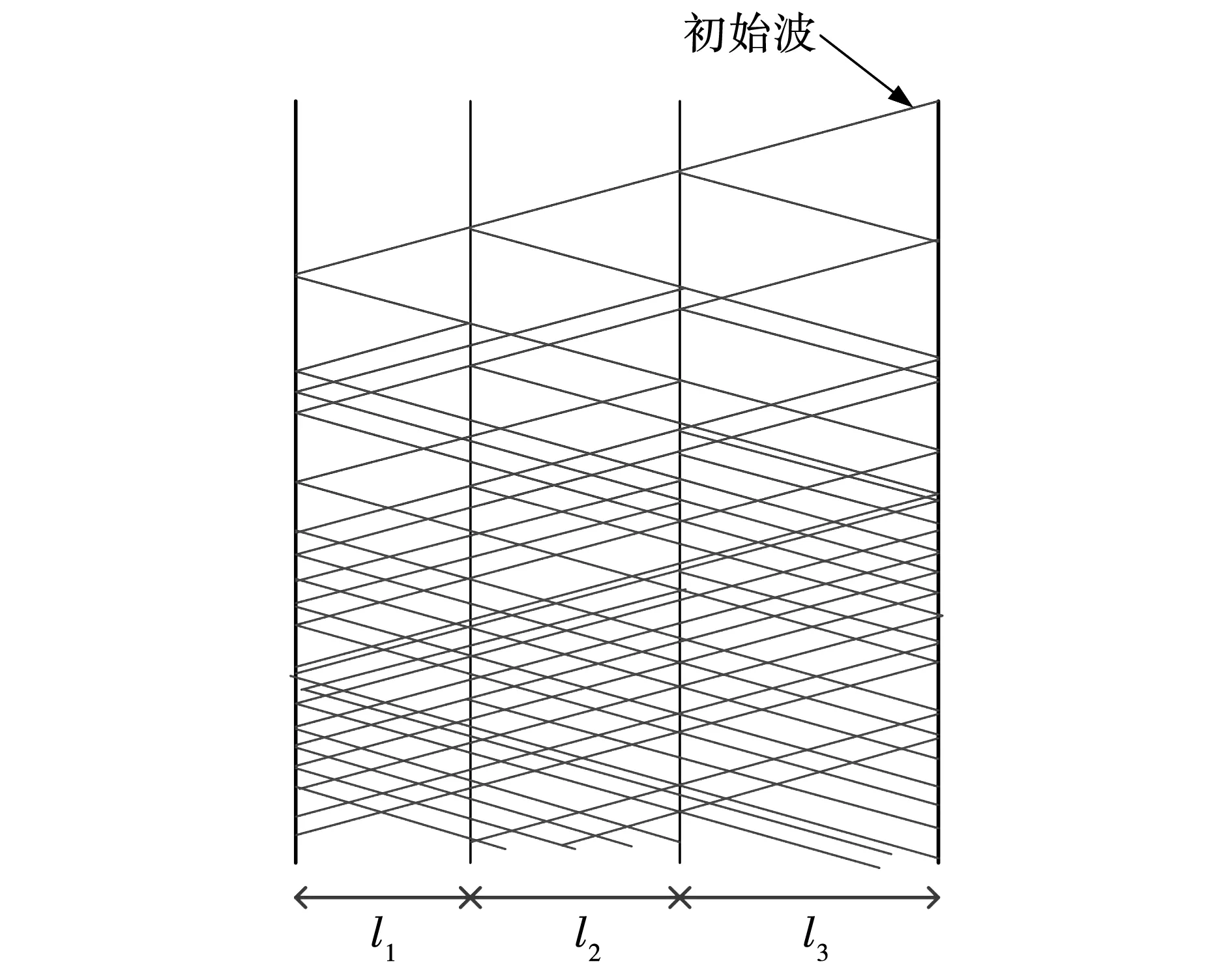
图1 行波在交叉互联电缆中的折反射示意图Fig.1 Schematic diagram of refraction and reflection of traveling wave in cross-bonding cables

双端法要求待测线路两端分别安装FLT，依据从两个FLT获取的同步时域数据来推算故障位置[12]，其时域数据监测过程如图2所示。在测得时域数据后，将两个FLT的数据发送到一个公共数据处理点，即可确定故障位置为

(1)

式中：l表示传输线的长度；x表示故障位置与较近的故障定位终端之间的距离；vn表示模式n对应的波速；τd表示两个故障定位终端监测结果的时间差。

图2 双端法故障定位示意图Fig.2 Schematic diagram of fault location by two-terminal method

1.3节将对双端法在交叉互联电缆系统故障定位中的可行性进行验证。

1.2 行波的模式及其对应特性

以某三相交叉互联电缆系统为例进行分析。该系统采用水平敷设方式，其位置关系如图3所示。图中：单相电缆采用缆芯-绝缘-屏蔽-绝缘的双导体结构，r1=20 mm，r2=40 mm，r3=41 mm，r4=46 mm；每两相电缆之间的水平距离D=0.5 m；电缆的埋深H=1.5 m。

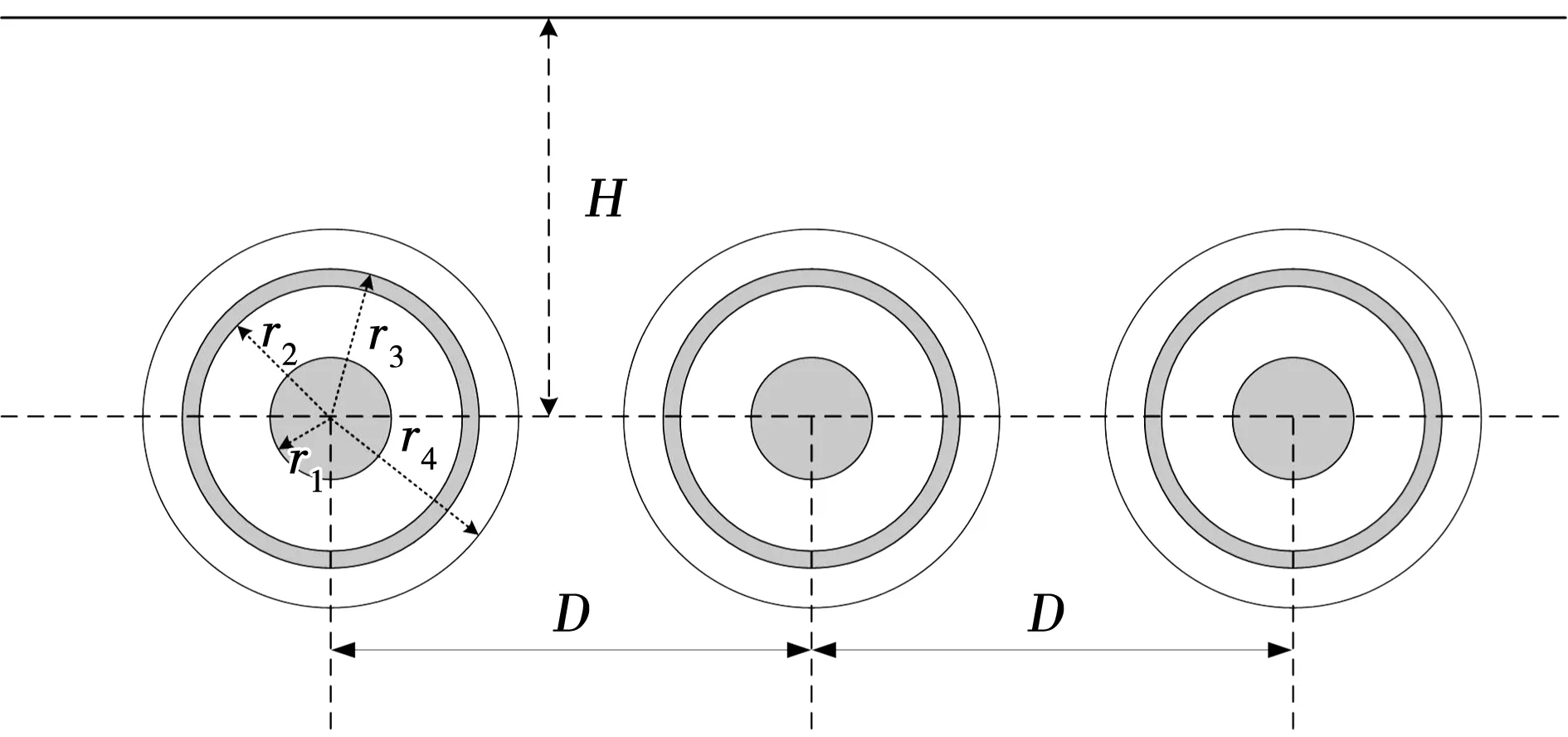
图3 三相交叉互联电缆系统同轴截面图Fig.3 Cross section of three phase cross-bonding cable system

该模型的电气参数设置如下：导体、绝缘、空气以及土壤的相对磁导率全部设置为1；缆芯的电导率σc=3.33×107S/m，屏蔽的电导率σs=2.74×107S/m；内绝缘的相对介电常数εr1=2.7，外绝缘的相对介电常数εr2=2.25；土壤的电导率σg=0.01 S/m。

对于图3中的三相交叉互联电缆系统，可以列出以下时域电报方程：

(2)

式中：U表示系统中导体的电压向量；I表示系统中导体的电流向量；Z表示串联阻抗矩阵；Y表示并联导纳矩阵。由式(2)可以推导出系统中导体的二维波动方程为：

(3)

式(3)表明，电缆系统中的导体在相域中存在电磁耦合，而通过相模变换理论可以对其进行解耦。构造合适的方阵S、Q，通过变换对U=SUm、I=QIm，即可将相域中的导体电压U与电流I转换为模域中的导体电压Um与电流Im，通过转换后的模域二维波动方程即可推出各模式下的衰减常数与波速[13]。

由于串联阻抗矩阵Z和并联导纳矩阵Y与频率相关，因此变换矩阵S、Q也具有频率相关性，且为复矩阵。文献[14]指出，在高频下(通常认为>1 MHz)，变换矩阵S、Q的虚部可以忽略不计、实部几乎固定，且变换后各模式的波速几乎固定，这一性质成为利用行波法对电缆故障进行定位的重要基础。

对于含有n个导体的电缆系统，其存在n个独立的模式[15]。针对1.2节中的三相6导体电缆系统，其存在6个独立的模式，且每个模式都有相应的波速，该电缆系统在高频下(1 MHz)的变换矩阵Q可表示为

(4)

式(4)中，变换矩阵Q的每一列元素都代表某种模式下对应的相域电流分布，其分布如图4所示。Q的第1列代表接地模式，第2、3列分别代表内护层模式1、2，而第4、5、6列分别代表同轴模式1、2、3。

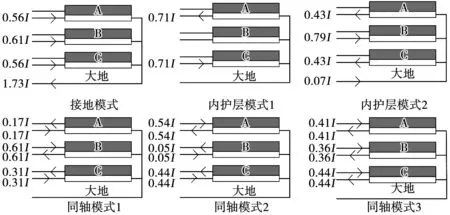
图4 不同模式对应相域电流分布示意图Fig.4 Schematic diagram of phase domain current distribution corresponding to different modes

随着频率升高，各模式对应的波速逐渐上升，且在高频下(1 MHz及以上)逐渐固定[14]。表1给出了1.2节中电缆系统高频下各模式对应的波速。由表可知，对于上述三相交叉互联电缆系统，3个同轴模式(下文记为同轴模式波群)在高频下的波速相等，且大于接地模式及内护层模式的波速。

因此，使用FLT监测故障信号时，同轴模式波群的故障信号将最先被接收，可用于双端法对故障进行定位。

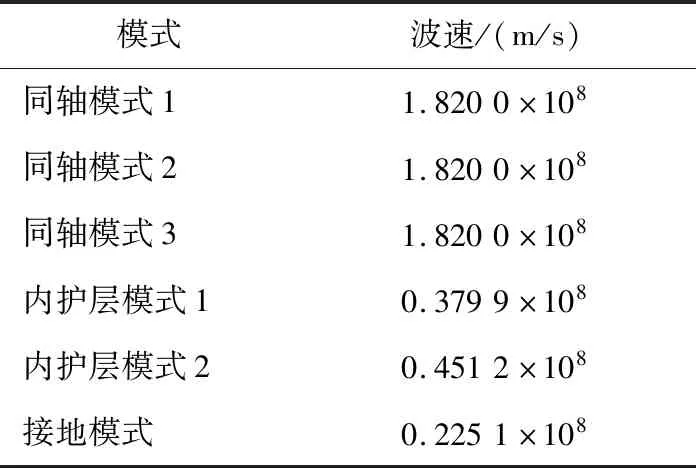
表1 高频下各模式对应的波速Table 1 Wave velocity corresponding to each mode at high frequency

1.3 同轴模式波在交叉互联电缆系统中的传播

为了研究利用同轴模式波监测交叉互联电缆系统故障的可行性，在PSCAD-EMTDC中建立如图5所示的交叉互联电缆模型进行验证，图中电缆的电气参数以及几何排布采用1.2节中的电缆模型设置。

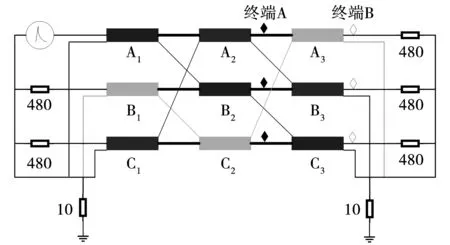
图5 单主段交叉互联电缆系统示意图Fig.5 Schematic diagram of one major section cross-bonding cable system

该模型模拟了暂态波在一个交叉互联主段上的传播，假设该主段接于两变压器之间。主段分为3个小段，每个小段的长度都为3 km，小段之间采用交叉互联连接方式，冲击信号通过左端A相缆芯输入线路，线路两端的变压器可简化为冲击电阻模型，故设置线路主段的左右两侧缆芯、护套通过如图5所示的连接方式接地。

对于上述仿真模型，设置输入信号为1.2/5 μs、幅值为27 kV的冲击电压信号，且冲击源的内阻抗设置为12 Ω。完成暂态输入信号的设置后，在线路的终端A处(实心菱形处)与终端B处(空心菱形处)分别添加电压互感器，以监测暂态波在交叉电缆系统中的传播。终端A与终端B处仿真所得的暂态电压波形如图6所示。

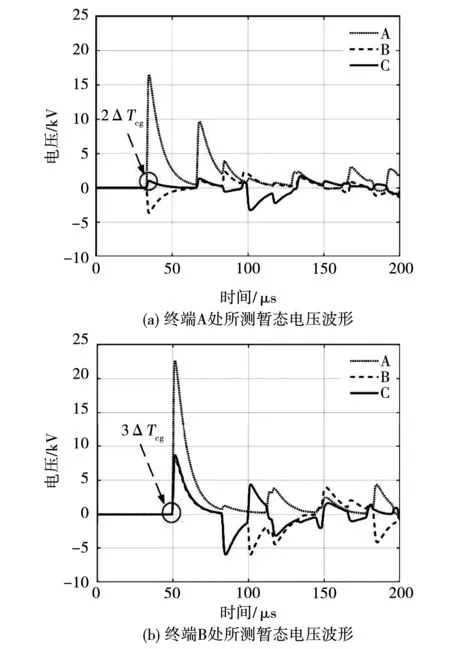
图6 测点暂态电压波形图Fig.6 Transient voltage waveforms of measuring points

由表1可知，对于交叉互联电缆系统，高频下同轴模式波群的传播速度最快，因而电缆两端的FLT将最先监测到同轴模式波信号。记同轴波在一个小段(3 km)内的传播时间为ΔTcg，则有

(5)

由图6可知，从施加冲击信号至终端A处测量到第一波的时间为2ΔTcg，至终端B处为3ΔTcg，这说明同轴波的波速在交叉互联系统中不受影响，FLT将最先监测到同轴模式波而非其他模式波，因而可以选择同轴模式波作为双端法故障定位所需的模式。

图6中，除第一波外，FLT还监测到了第二波、第三波等波形。此外，故障相监测到的电压幅值比非故障相高。以上现象是因为在线路两端及交叉连接处阻抗存在不连续性，由此会带来大量的折反射，除确定为同轴模式波的第一波外，随后到达的波可能经过复杂的折反射过程，无法确定其对应于何种模式，这也印证了单端法无法应用于交叉互联电缆系统的故障定位。

2 交叉互联电缆系统故障定位策略研究

2.1 自动故障定位系统设计

对于电力电缆而言，故障并非频繁发生，需要熟练技术人员操作的故障检测系统成本较高，从经济成本考虑，实现自动化监测的故障定位系统无疑是最佳选择。

图7给出了交叉互联电缆实现自动化故障定位的系统框图，图中虚线框内的单元即为FLT。当交叉互联电缆系统出现故障后，由故障引起的同轴模式波将沿轴向向两个FLT传播。随后，同轴波进入FLT，经由电压互感器进入高频故障暂态记录仪进行采样，通过两个同步单元控制高频暂态记录仪以及触发单元的同步记录。触发单元的作用仅仅是判断故障是否发生，若监测到故障发生，则FLT将采样信号发送至中央数据处理单元，利用算法对故障进行定位。

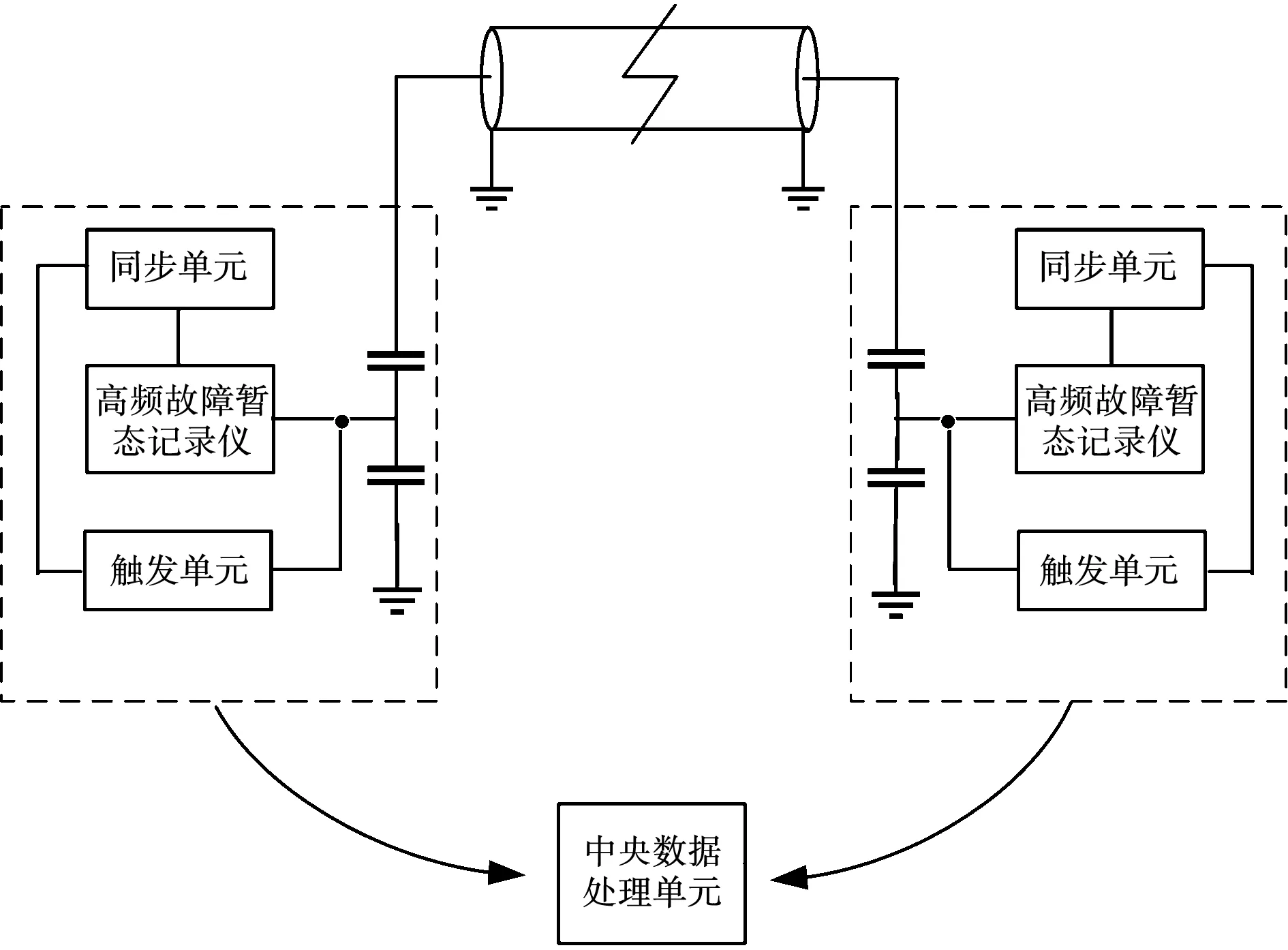
图7 自动化故障定位系统框图Fig.7 Block diagram of automatic fault location system

采样信号进入中央数据处理单元后，需要对采集的信号进行处理，并设计算法对故障进行判断。不同于传统的小波变换故障定位方法[8-10]，本文利用变分模态分解(variational mode decomposition,VMD)改进后的希尔伯特黄变换对故障信号进行时频分析，并设计一种新的判据对故障信号的发生与定位进行识别。

2.2 基于VMD改进的Hilbert-Huang变换

经验模态分解(empirical mode decomposetion,EMD)是希尔伯特黄变换的第一步，EMD能够自适应地将未知信号分解为若干个内涵模态分量之和，克服了小波变换中无法灵活选择小波基的弊端[16]。

然而，EMD分解过程中极易出现模态混叠现象，使得分解结果失去意义。例如，在一个连续低频正弦信号上叠加间歇性高频震动的调制信号，利用EMD分解得到的本征模态函数将包含差异极大的特征时间尺度，这将导致内涵模态分量失效，图8为利用EMD分解导致模态混叠的过程。

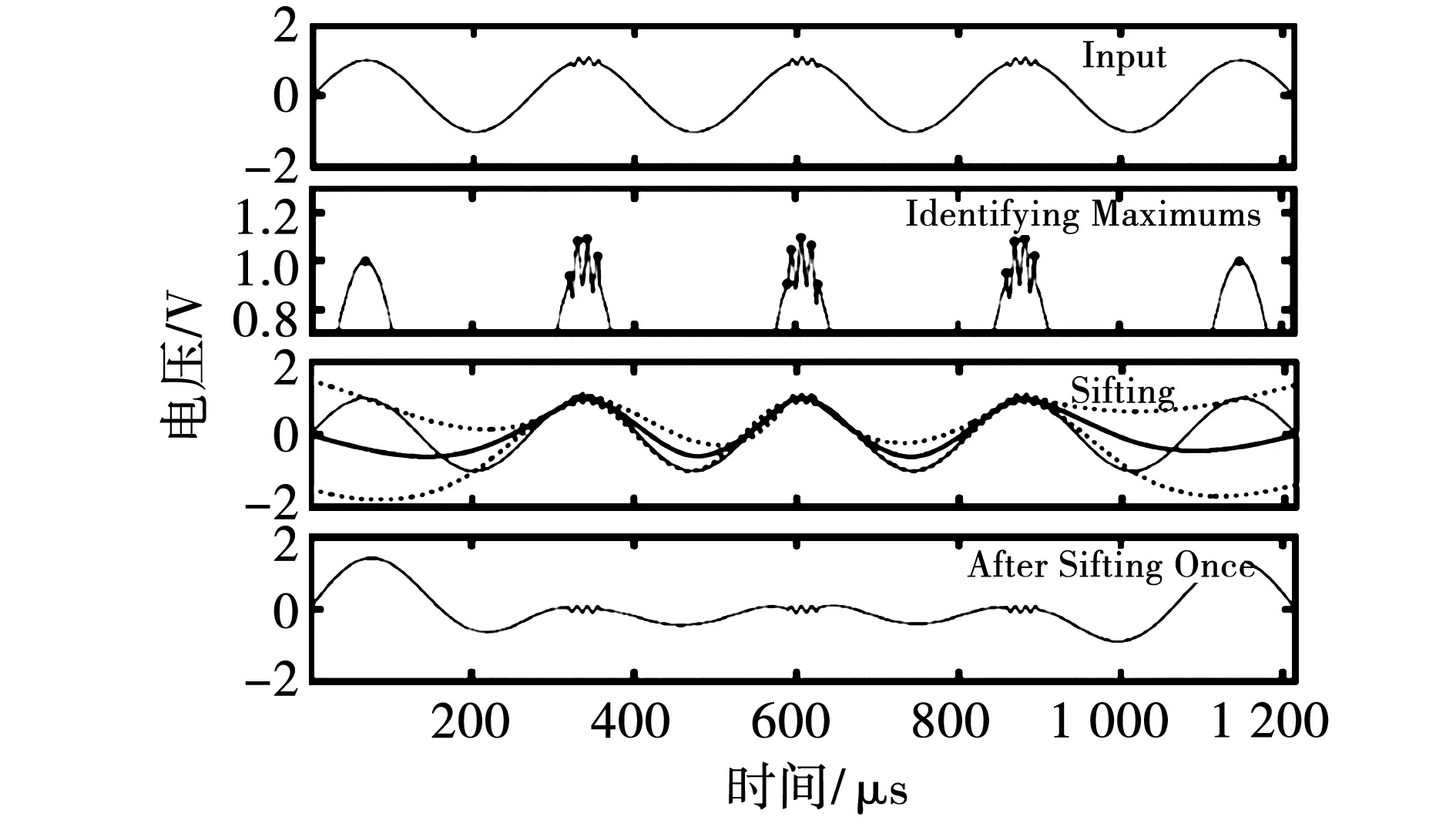
图8 模态混叠过程示意图Fig.8 Schematic diagram of mode mixing process

VMD是一种非递归信号处理方法，将信号分解过程转化为变分问题，使用VMD代替希尔伯特黄变换中的EMD可以避免模态混叠现象[17]。图9为VMD对类似信号的分解结果，克服了对此类信号使用EMD分解易产生模态混叠现象的缺陷。

VMD可自适应匹配每个内涵模态分量的最优中心频率和带宽，VMD分解的目的在于寻找约束变分模型下，使得每个内涵模态分量中心频率带宽之和最小的模态函数ui(t)。约束变分模型的推导及求解过程如下[18]：

1)通过对信号f(t)的模态函数ui(t)进行变换，求取每个模态的解析信号及其单边频谱，表达式为

(6)

式中：δ(t)表示狄拉克分布；*表示卷积运算。

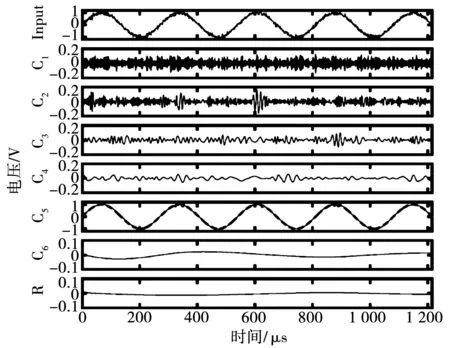
图9 变分模态分解过程示意图Fig.9 Schematic diagram of VMD process

2)通过引入指数项调整各模态函数估计的中心频率，调制每个模态函数的频谱到其相应的基频带，表达式为

(7)

式中ωi为ui(t)的中心频率。

3)通过解调信号梯度的平方范数，估计出各模态函数的带宽，则相应的约束变分模型为：

(8)

式中：{ui}={u1,…,uk}；{ωi}={ω1,…,ωk}；k为内涵模态分量的数量。

通过引入二次惩罚因子α和Lagrange乘法算子λ，约束变分问题可转化为如下非约束变分问题：

(9)

VMD中采用乘法算子交替方法项(alternating direction method of multipliers,ADMM)解决以上变分问题，ωi和ui在2个方向加以更新，表达式为：

(10)

(11)

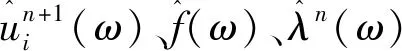
(12)

式中γ表示容许误差。

希尔伯特谱是希尔伯特黄变换得到的最直观结果，反映了信号时间、瞬时频率和幅值之间的关系，可以用于分析包含混合分量信号的各分量随时间变化的规律，以识别局部特征[19]。

1)对每一个内涵模态分量ui(t)(i=1,…,k)作Hilbert变换，获得信号的瞬时参数谱为

(13)

2)根据ui(t)和vi(t)可以构建一个解析信号为

zi(t)=ui(t)+jvi(t)=ai(t)ejθi(t)。

(14)

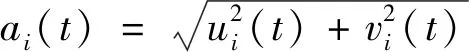
3)在Hilbert-Huang变换中，可以定义瞬时频率为

(15)

4)希尔伯特谱为

(16)

2.3 故障定位算法设计

实际上，采样信号的时频分析是通过离散希尔伯特黄变换实现的。使用离散希尔伯特黄变换分析程序可以求得二维矩阵形式的离散Hilbert谱如图10所示，矩阵中的每个元素表示该时刻该频率成分的强度，Δf和Δt分别表示离散条件下的单位频率间隔和单位时间间隔[20-22]。

离散Hilbert谱的频率范围可以进行灵活设置，一般来说，0～1 MHz的频率范围足以对电缆的故障信号进行分析。

图10 离散希尔伯特谱示意图Fig.10 Schematic diagram of discrete Hilbert spectrum

当线路两端的FLT对信号进行采样后，测得的采样序列在FLT中进行保存，并对该采样序列进行降采样处理。利用快速傅里叶变换(fast Fourier transform,FFT)计算降采样序列的频谱能量[23]，如果大于给定的阈值，则认为在采样序列内发生了故障，FLT将采样序列发送至中央数据处理单元进行故障定位。图11为采样信号分析的总体框架。

1)信号的预处理。由于行波在交叉互联电缆传输过程中会产生大量的折反射导致能量衰减，所以将所测A、B、C三相的信号进行叠加作为分析算法的输入。这样不仅可以增强信号的能量，还可以抵消信号中的工频成分，便于分析。

2)序列重组。由于采样信号为截断序列，对于含卷积运算的变换而言，其在序列的首端和末端会出现异常突变，这种现象称为端点效应(End Effect)。解决的方法是用上一个采样序列的一部分填充本次的采样序列，实现序列的重组。

3)定位判据。当某一时刻电缆发生故障时，该时刻对应的信号变化率较高，信号中所含的高频分量急剧增加。因此，在离散Hilbert谱中，可以认为某一时刻信号的高频成分越高，该时间发生故障的可能性越大，可以建立权信号强度判据，表达式为

(17)

式中：Jj表示j时刻按频率权重计算的信号强度；x表示离散Hilbert谱的频率点数量；hij表示j时刻频率点i所对应频率的强度。

4)阈值选择。在实际应用时，可以对正常工况下的信号进行多次采样，对采样信号进行降采样处理后，利用FFT计算所有样值序列的平均信号能量，表达式为

(18)

式中：TSV表示判断故障是否发生的阈值；N表示样值序列的数量；Ei表示第i个降采样序列的信号能量；η表示安全裕度。

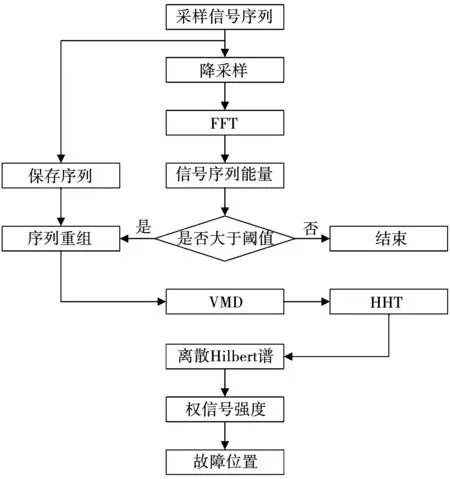
图11 采样信号分析总体框架Fig.11 Overall framework of sampling signal analysis

3 案例分析

3.1 模型设置

本文在PSCAD-EMTDC中搭建了三主段双端供电220 kV电缆系统如图12所示。系统的两侧以500 kV集总参数电压源模拟500 kV的电网，使用3个交叉互联主段(每段9 km)模拟电缆线路，每个主段包含3个长度为3 km的电缆小段，电缆的几何及电气参数与1.2节中的电缆模型设置相同。线路的两端接于容量为500 MVA的电力变压器，变电站的接地电阻及交叉互联段之间的接地电阻如图12所示。

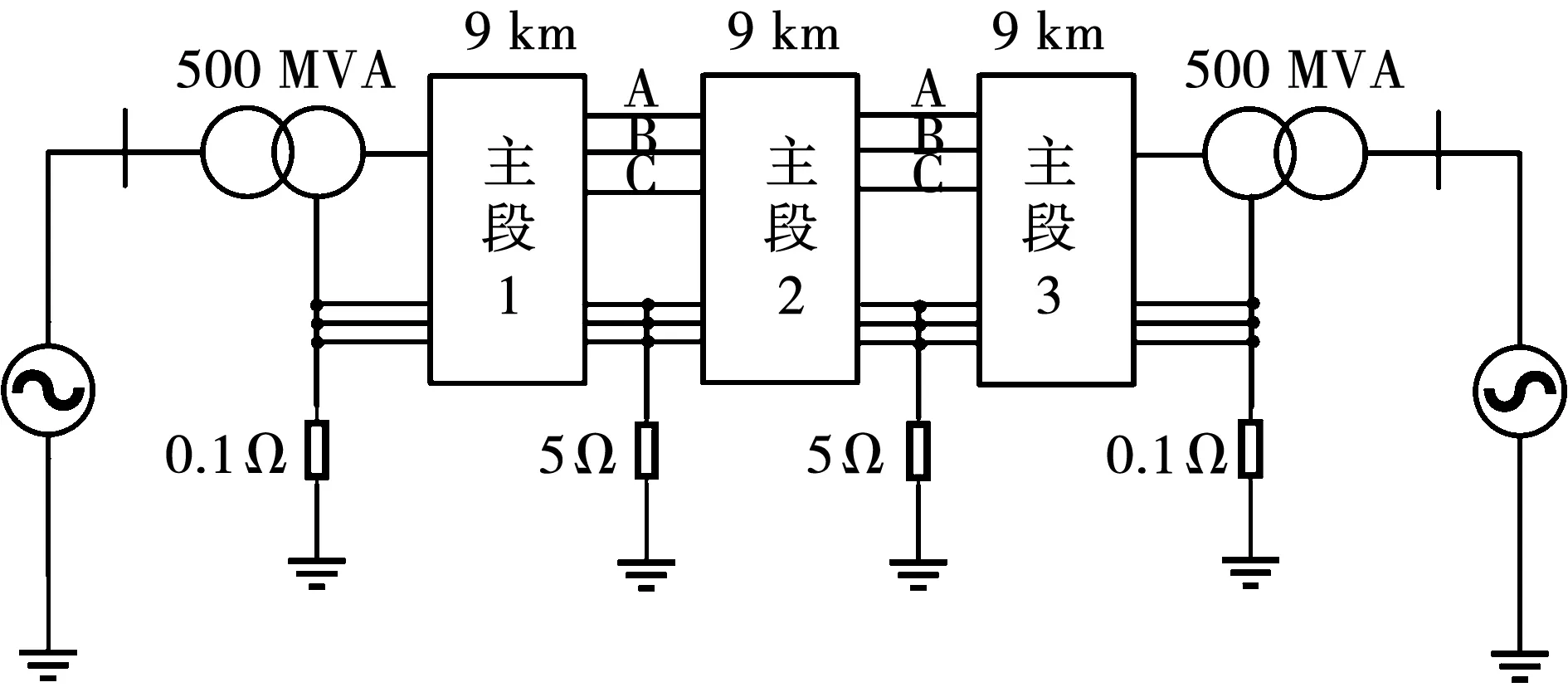
图12 三主段双端供电系统示意图Fig.12 Schematic diagram of double terminal power supply system of three major sections

图13为模型故障设置的示意图，设置A相绝缘击穿和A相单相接地为故障类型。故障1设置在电缆小段的正中，距离送端4.5 km；故障2设置在交叉互联主段的连接处，距离送端9 km；故障3设置在电缆小段的连接处，距离送端15 km。

图13 模型故障设置示意图Fig.13 Schematic diagram of model faults setting

系统中，信号的采样频率设置为10 MHz，采样序列包含10 000个样本。若新的采样序列中存在故障，则使用上一个正常工况采样序列的40个样本填充所测序列，实现对序列的重组，消除端点效应。

3.2 结果及分析

以故障2处发生A相绝缘击穿为例，对定位算法的执行流程进行分析，具体流程如下：

1)在PSCAD中设置故障后，在电缆线路两端对信号进行采集，采集后对采样序列进行重组，并施加5%随机噪声以模拟现场环境如图14所示。

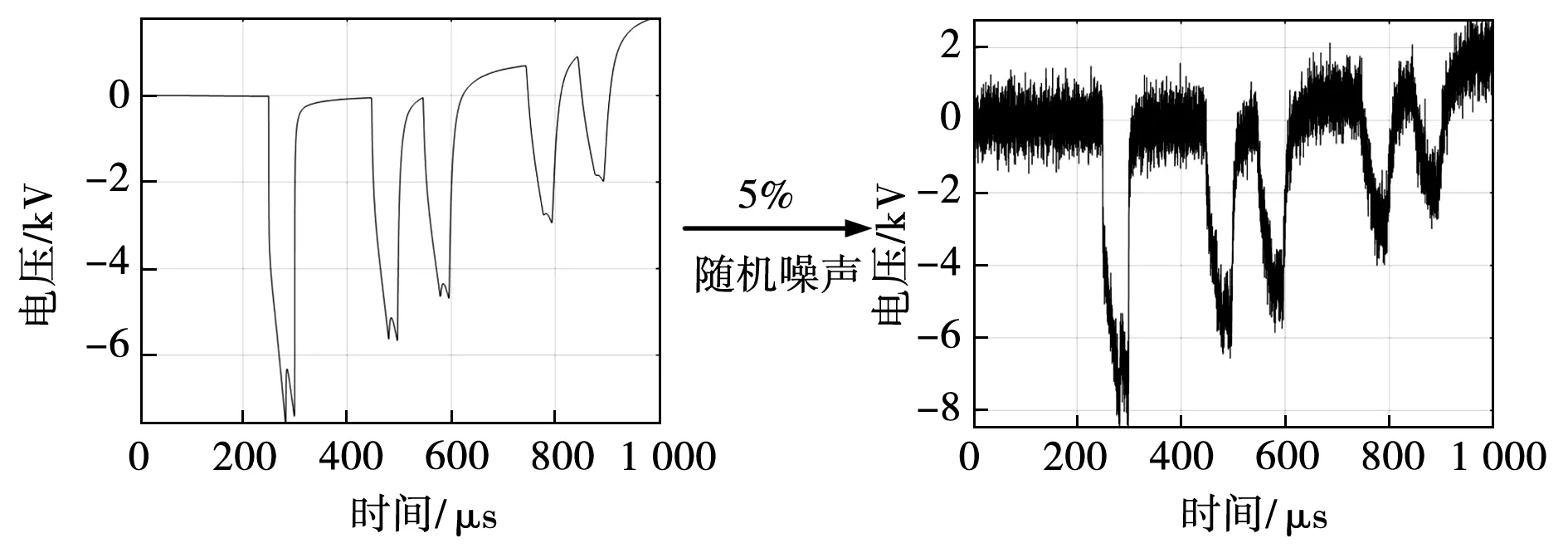
图14 信号加噪处理Fig.14 Noise-adding of the signals

2)信号加噪后，使用图11所示的分析流程得到重组后采样序列的权信号强度，并删除添加的40个样本点对应的权信号强度值。图15为电缆线路两侧所测故障信号的权信号强度序列。

3)得到送端及受端所测信号的权信号强度序列后，其第一波到达对应的峰值时刻如图15所示。利用送端及受端第一波到达的时间差，结合式(1)即可求出故障所在位置。

表2给出了不同位置的故障对应的故障定位结果。由表可知，对于不同位置处的绝缘击穿及单相接地故障，使用改进Hilbert-Huang变换以及权信号强度判据进行定位，其定位精度十分良好，相对误差均在1.2%以内。

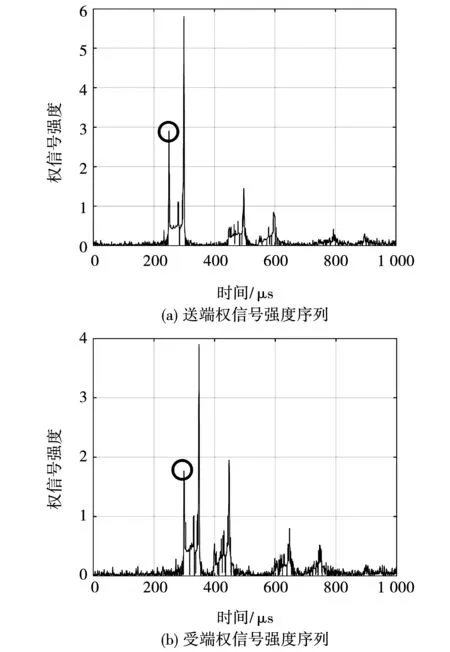
图15 送端及受端权信号强度序列Fig.15 Weighted signal strength sequences of the sending end and receiving end

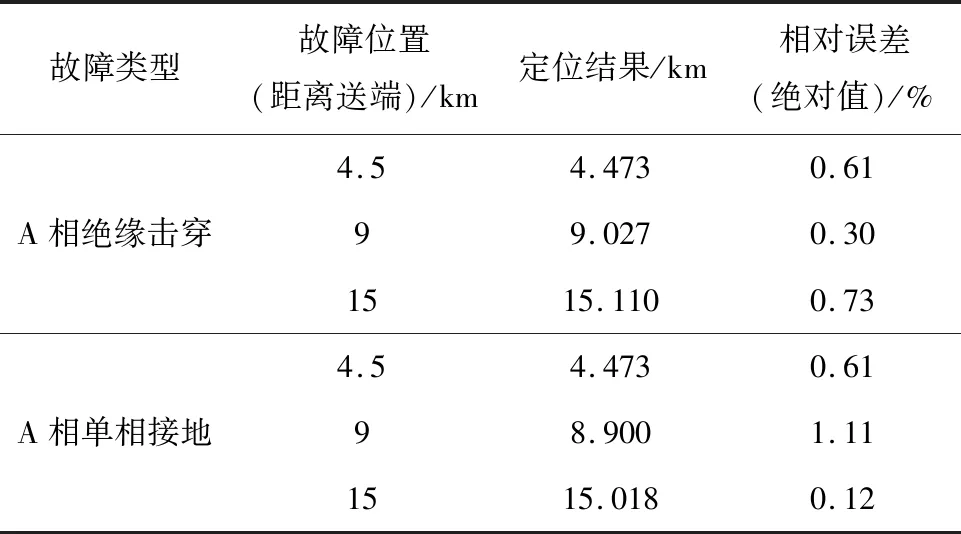
表2 高频下各模式对应的波速 Table 2 Wave velocity corresponding to each mode at high frequency

4 结 论

本文针对交叉互联电缆系统提出一种基于改进Hilbert-Huang变换和权信号强度判据的在线故障定位方法，主要结论如下：

1)对于交叉互联电缆系统，同轴模式波群拥有最快的波速，且同轴模式波群在交叉互联电缆中的传播不受交叉连接方式影响，可以用于交叉互联电缆的故障定位。

2)行波在交叉连接处、电缆端部及故障位置处会产生复杂的折反射过程，这将导致同轴模式波的第二个到达时刻很难识别，因此单端法不适用于交叉互联电缆的故障定位。

3)基于改进Hilbert-Huang变换和权信号强度判据的故障定位方法具有良好的自适应性，对于4.5、9和15 km处的绝缘击穿和单相接地故障定位的相对误差在1.2%以内，证明该在线故障定位方法具有良好的效果。

4)交叉互联电缆线路中，电缆接头模型对故障定位方法的影响还需进一步深入研究。