低转矩脉动同步磁阻电机磁障形状分析与优化设计

刘成成，刘乾宇，王韶鹏，汪友华

(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2.河北工业大学 河北省电磁场与电器可靠性重点实验室，天津 300130)

0 引 言

近年来稀土材料愈发紧缺，同步磁阻电机(synchronous reluctance machine,SynRM)由于无需稀土永磁励磁且性能优异受到广泛关注。目前，其广泛应用于机床主轴、电动汽车以及纺织设备等场合中[1-4]。与异步电机相比，SynRM同步运行，效率较高[5]。与永磁同步电机相比，SynRM无需永磁励磁，可靠性高且成本较低，但功率因数和效率也较低[6]。与开关磁阻电机相比，其控制简单、转矩脉动和噪声小[7]。综上，SynRM在成本、性能等方面均存在一定的优势，但其还存在功率因数低、转矩脉动大等问题，这些问题制约了SynRM的发展。

文献[8]研究了SynRM相邻磁障的宽度比值对转矩脉动的影响，提出一种渐变式磁障结构，有效减小了电机的转矩脉动。文献[9]提出一种转子缺口设计方法，用于减小SynRM的转矩脉动。文献[10]对转子磁障端部尺寸进行了优化，以改善电机的转矩性能。文献[11]研究了能够降低SynRM转矩脉动的不对称结构，兼顾降低转矩脉动、提高效率。文献[12]提出采用移动渐近线法实现基于平滑heavisidei函数的拓扑优化方法，对转子结构进行优化，改善电机的转矩性能。SynRM转矩脉动主要来源于凸极转子磁阻变化，优化SynRM转子磁障形状能够有效减小转矩脉动，本文提出一种磁障的形状优化方法，能够获得相应层数的最佳磁障形状。

形状优化用于确定结构的边界形状或内部的一些几何形状。形状优化和拓扑优化都属于结构优化，但拓扑优化相比于形状优化更复杂，拓扑优化以材料分布为优化对象，需考虑穿孔或漂浮的材料碎片问题[12]。文献[13]提出一种新的拓扑优化方法，将一组离散设计空间的单元格作为控制器，通过控制器在网格中移动留下材料痕迹，使其运动在设计空间中，优化材料分布。传统拓扑优化方法中有限单元的大小和形状限制了电机的最优结构。而针对SynRM的设计，在相关设计经验的支撑下，形状优化能够取得较好的优化结果。

为降低转矩脉动，本文首先改变传统SynRM转子磁障设计方法，提出用分段线性插值法确定一些离散的点，形成转子磁障的边，在转子设计域中不改变材料的特性。针对定转子的设计变量较多的问题，提出试验设计优化方法和全局优化方法[14]相结合的方法，减小高维参数优化所需有限元计算次数。最后以一层和两层磁障的SynRM为例进行对比分析，验证本文提出方法的有效性。

本文重点研究同步磁阻电机的磁障形状设计方法，提出采用分段线性插值法建立同步磁阻电机的磁障形状。分析表明，通过改变相关形状参数能够遍历同步磁阻电机的主要磁障结构设计，如能够获得传统两层磁障同步磁阻电机的磁障形状、棋盘图案的转子模型等，当磁障边界所取的点数较多时，也可近似获得C型磁障同步磁阻电机。磁障形状优化后的同步磁阻电机与文献[13]中拓扑优化方法优化后的同步磁阻电机相比，具有较好的转矩性能和更简单的磁障形状，且优化所需时间短。

1 磁障形状建模方法

SynRM的电磁转矩与其直交轴电感差值成正比，基于坐标变换理论，SynRM的空间矢量图如图1所示。图中：is为定子电流矢量；id、iq分别为直轴电流分量和交轴电流分量；Ld、Lq分别为直轴电感分量和交轴电感分量；ωs为电机的电角速度；us为定子电压矢量；β为is与d轴的夹角；α为is与us的夹角；γ为is和q轴的夹角。SynRM的直交轴电感、电磁转矩、凸极率和功率因数分别表示如下：

1)直轴与交轴电感为：

(1)

(2)

2)电磁转矩为

(3)

式中p为电机的极对数。

3)凸极率为

(4)

4)功率因数为

(5)

(6)

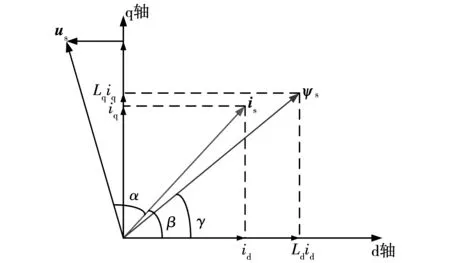
图1 SynRM空间矢量图Fig.1 Space vector diagram of SynRM

确定磁障形状的本质是确定磁障上下层边的线，而线决定于点，因此确定出线上的关键点是关键。本文通过线性插值确定磁障边上的关键点，实现转子磁障复杂形状且保证其上、下边互不干涉。在SynRM中，增加磁障层数能提高凸极率，进而提高转矩与功率因数。以表1的电机为对象，给出磁障上、下边界上关键点坐标的表达式，以建立一层磁障SynRM的上边界和下边界为例，阐明线性插值法建立转子磁障的步骤。

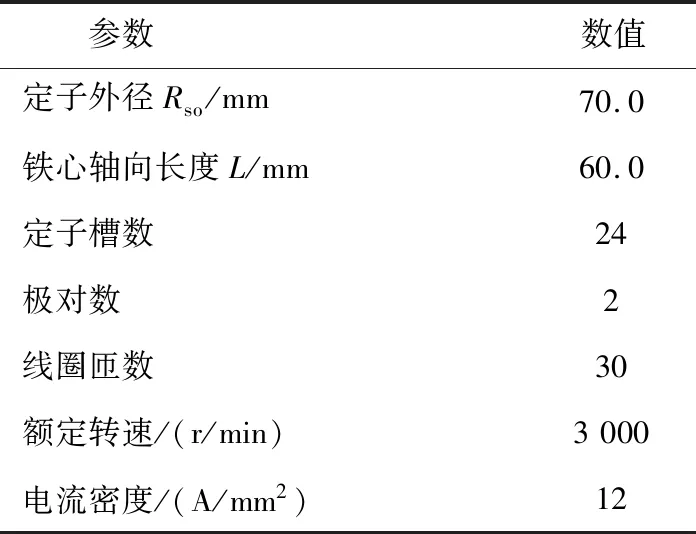
表1 SynRM主要参数Table 1 Main parameters of SynRM

(7)

各个关键点与y轴之间的夹角满足：

(8)

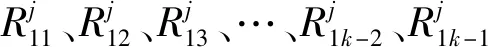
(9)

已知磁障右半部分下边界各点的坐标表达式，图2(a)为一层磁障下边界各点建模示意图。同理，在第j层磁障右半部分上边界的两个端点之间插入k-1个关键点，图2(b)为一层磁障上下边界各点建模示意图。

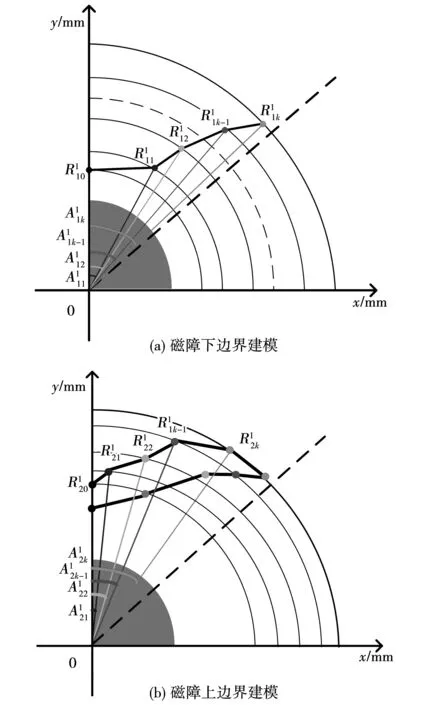
图2 一层磁障边界建模Fig.2 First-layer magnetic barrier boundary modeling

应用上述方法能够保证确定的每一个点都在SynRM的设计域内，k为大于1的正整数，k的取值越大，组成磁障边界所取的点数越多，磁障边界线段越多，可以形成的转子形状越多。考虑到电机优化所需的计算量和电机加工工艺，两层磁障SynRM用分段线性插值的方法建立转子模型时，模型中磁障每一条边界k的取值为5，两层磁障SynRM磁障形状优化模型如图3(a)所示；通过对形状参数进行改变能够遍历绝大多数的磁障形状，获得传统两层磁障SynRM模型如图3(b)所示；文献[13]中棋盘图案的转子模型如图3(c)所示；当磁障边界所取的点数较多时，也可获得C型磁障SynRM如图3(d)所示。

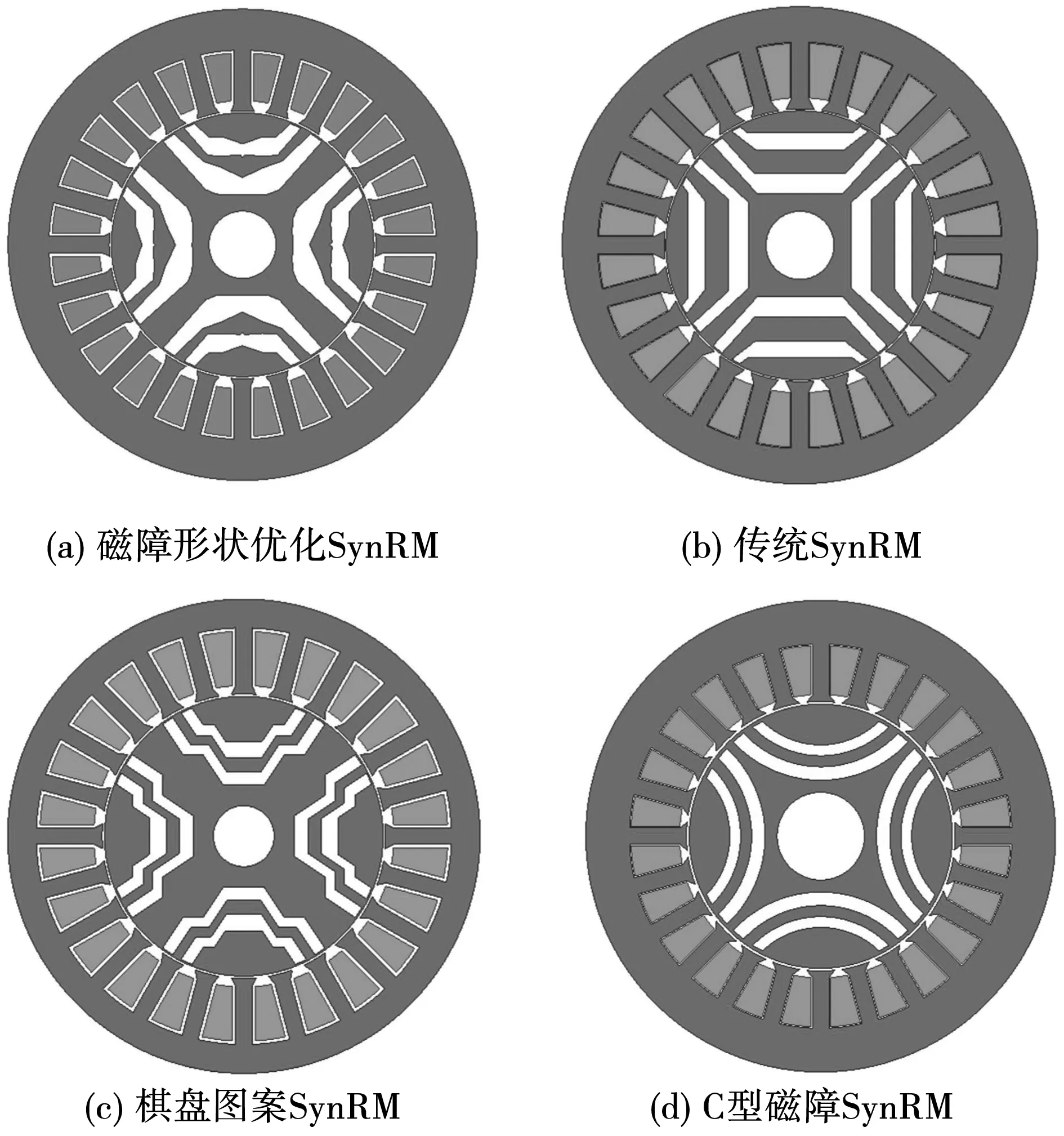
图3 两层磁障SynRM模型Fig.3 Two-layers magnetic barrier SynRM model

2 SynRM磁障形状优化

为获得定转子各参数的最优值，解决高维参数优化中计算量较大的问题，本文提出试验设计优化方法和全局优化方法相结合的多目标优化方法。优化流程主要分为5个部分：1)应用序贯田口优化方法对定子参数进行优化；2)用拟牛顿优化方法对转子一层磁障形状进行优化，当目标函数值O2收敛时，进行下一步优化；3)应用拟牛顿优化方法对转子第二层磁障形状进行优化，当目标函数O2值收敛时，进行下一步优化；4)应用序贯田口稳健优化方法继续优化定子参数，目标函数值下降百分比收敛至小于0.3%，定子优化结束；5)继续对转子所有参数进行全局优化，直至目标函数收敛，优化结束。最后，对比分析传统SynRM与进行磁障形状优化的SynRM的转矩、效率等性能。

2.1 SynRM定子优化

对SynRM的转子磁障形状进行优化，其定子仍为传统结构，参数较少，采用序贯田口稳健设计方法(sequential Taguchi robust optimization method,STROM)对定子参数进行优化设计。通过对定子参数进行第一轮优化，能够快速找出减小转矩脉动的定子参数大致范围，提高优化效率。其中电机裂比定义为S，表达式为

(10)

式中：Rso为定子外半径；Rro为转子外半径。首先优化电机裂比，优化后确定电机的裂比为0.56。此时，电机的平均转矩(average torque)为12.3 N·m、转矩脉动(torque ripple)为0.716。考虑到文献[15]指出优化定子齿宽，选取合适定子齿宽可以增大电机平均输出转矩。文献[16]指出定子齿部厚度和轭部厚度设计准则，表明定子齿部和轭部对电机转矩脉动有影响。文献[17]提出定子齿槽型的结构及气隙中的磁场分布会使电机出现一定的齿槽转矩和转矩脉动，对电机的噪音和震动具有一定的影响。参考上述文献中研究成果，结合本文优化目标，选取定子靴部高度(A)、定子齿高(B)、定子槽口宽(C)、定子齿宽(D)作为4个优化因子。

用序贯田口稳健优化方法对A、B、C、D4个参数进行优化，选取相应的控制参数水平、噪声因素水平，建立田口表计算每组参数的信噪比，得出每个参数对应水平的信噪比，目标函数的值越小，实验结果越好，确定此次实验控制因素的水平。

1)记录初始平均转矩、初始转矩脉动值；

2)选取4个优化因子范围以及每个优化因子4个水平值；

3)确定4个噪声因子的2个水平；

4)有限元仿真，根据下式建立序贯田口稳健优化方法的矩阵，即

(11)

式中：下标initial表示初始性能；i表示实验的组数；j表示每组实验进行的次数，用有限元进行16×8次计算。

5)根据下式确定16组实验数据的信噪比，即

(12)

由下式计算优化因子各水平信噪比，选取最大信噪比优化因子水平，确定实验最优解，即

(13)

6)将最优解代入有限元模型计算。

确定此次实验的最优解，在最优参数水平下，此次实验结果平均输出转矩为15.1 N·m，转矩脉动为0.613，此时目标函数O1值为1.68，最优解转矩脉动值下降了13.3%。

依据上述流程，当转子两层磁障形状优化结束后还需对定子的A、B、C、D4个参数进行优化，根据实验结果决定停止或继续实验。当目标函数O2收敛时，优化结束，确定最终优化结果，否则继续优化定子参数。对定子4个参数进行了4轮优化，达到目标函数收敛时，最优的定子靴部高度和齿高参数采样过程如图4所示，目标值变化过程如图5所示。优化后的仿真结果表明，转矩脉动值为0.736%，平均输出转矩值为15.4 N·m，转矩脉动下降了6.13%，验证了序贯田口法在电机优化设计中的实用性和可行性，应用该方法优化定子大大减少试验次数，缩短了两层磁障SynRM磁障形状优化的周期。

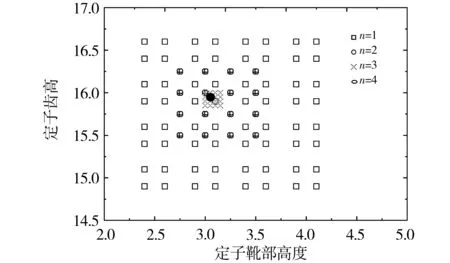
图4 定子靴部高度和齿部高度参数采样过程Fig.4 Sampling process of stator boot height and tooth height

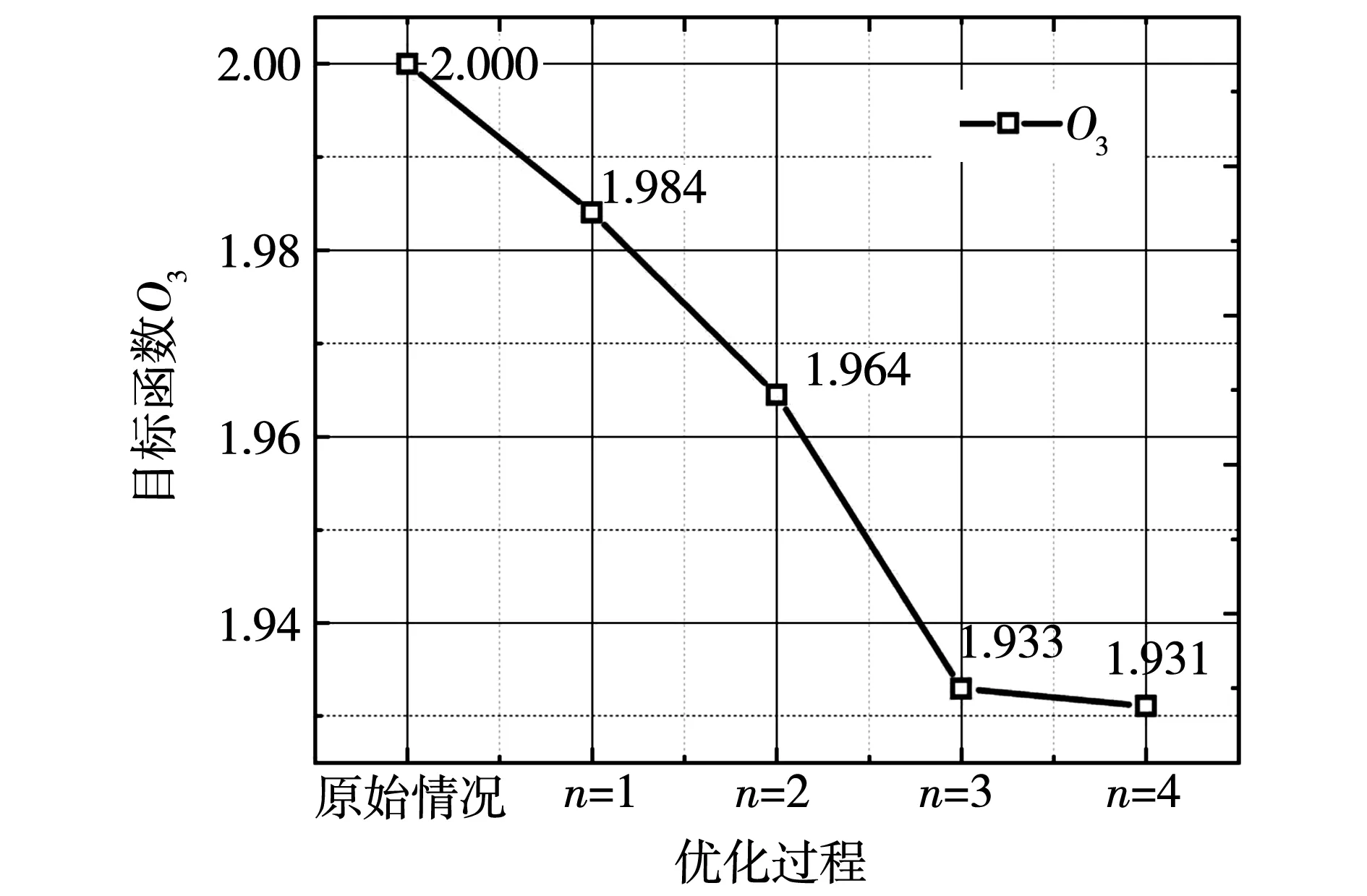
图5 目标值变化过程Fig.5 Target value optimization process

2.2 SynRM第一层磁障形状优化

对两层磁障SynRM的磁障形状进行优化涉及的转子待优参数较多，组成磁障边界关键点之间的插值系数相互关联，虽然每个系数有确定的取值范围，但这些系数对磁障边界的影响很大，各参数之间关系密切，本文选用拟牛顿法(quasi-Newton method)对转子参数进行优化[18-20]。

以传统两层磁障SynRM优化后转矩性能作为基值(平均转矩为15.3 N·m，转矩脉动为0.022 2)，对电机性能进行比较与讨论，定义目标函数为

(14)

式中：Ttra_ave_Torque表示传统两层磁障SynRM平均输出转矩；Ttra_Ripple表示传统两层磁障SynRM转矩脉动。

当目标函数O2的值大于1时，表明电机的转矩性能得到改善，O2的值越大表明性能越好。保持其他参数不变，优化第一层磁障相关的参数，目标函数为式(14)，Cost的值为目标函数的负值。当目标函数值收敛时，第一层磁障优化结束。拟牛顿优化过程中Cost收敛过程如图6所示，随着计算次数的增加，Cost取值会不断振荡。

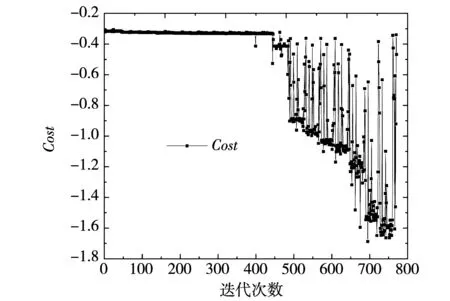
图6 优化第一层磁障参数迭代过程Fig.6 Iterative process of optimizing the parameters of the first layer of flux barrier

在第一层磁障参数优化过程中，随着Cost取值改变，电机转子形状过渡过程如图7所示。Cost取1.5时，两层磁障中直轴方向磁障形状与传统磁障形状相同，交轴方向磁障形状与传统磁障形状相比，磁肋变薄，减少了极间漏磁，从而提升平均转矩和功率因数[21-22]。此时，两层磁障SynRM磁障形状优化的平均输出转矩为15.5 N·m，转矩脉动为0.013。与传统两层磁障SynRM相比，平均输出转矩上升了1.23%，转矩脉动下降了41.4%。

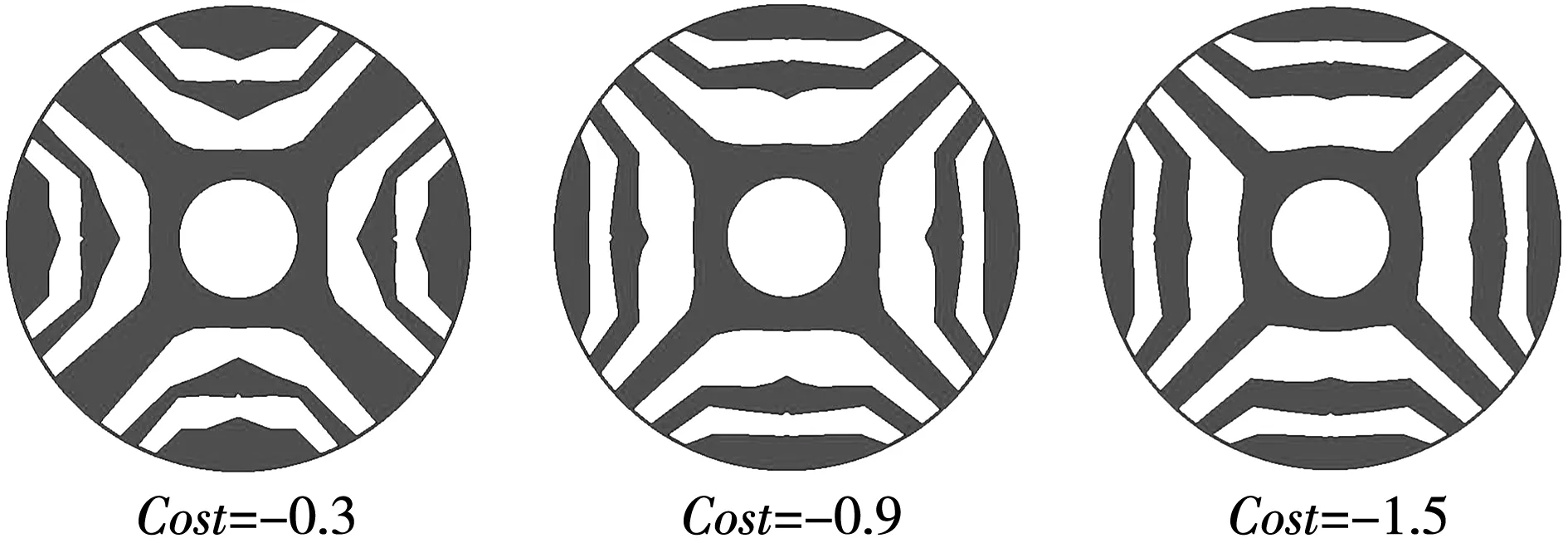
图7 第一层磁障参数优化过程中转子形状变化Fig.7 Rotor shape variation during the optimization process of the first layer of flux barrier

2.3 SynRM第二层磁障形状优化

保持其他参数不变，用拟牛顿优化方法优化第二层磁障的相关参数。Cost取值不再收敛时，优化结束。此时优化得到的电机与传统两层磁障SynRM相比，电机平均输出转矩提高了0.654%，转矩脉动下降了64.3%。

2.4 SynRM磁障形状优化

对转子所有待优化参数进行优化，直至目标函数O2不收敛，随迭代次数的增加，Cost的值在-3附近时不再收敛，此时两层磁障SynRM磁障形状优化转矩性能达到最优，优化结束。

3 SynRM磁障形状优化分析

SynRM输出转矩取决于其交直轴电感差值，且功率因数与凸极率正相关，增大凸极率能有效提高电机功率因数[23-24]。对SynRM而言，其转矩特性、功率因数和效率特性是最为重要的指标。本文选取如图3(b)所示的传统SynRM为基准，对比分析相同电流密度下，对磁障形状进行优化后的SynRM的平均输出转矩、转矩脉动、功率因数和效率等性能。

3.1 一层磁障SynRM性能对比

为验证磁障形状优化方法的有效性，对一层磁障SynRM同样采用序贯田口法和拟牛顿方法相结合的方法进行优化，其目标函数为O2，以优化后传统一层磁障SynRM转矩性能为对比依据。

传统一层磁障SynRM结构如图8(a)所示，对一层磁障SynRM磁障形状优化后的电机结构示意图如图8(b)所示。优化时选择峰值电流密度为12 A/mm2，两台电机的平均输出转矩、转矩脉动、铁心损耗与效率对比如表2所示。当电流密度为12 A/mm2时，对磁障形状进行优化，使得SynRM具有更高的平均输出转矩、更低的转矩脉动、较低的铁心损耗，且能有效提升电机运行效率。

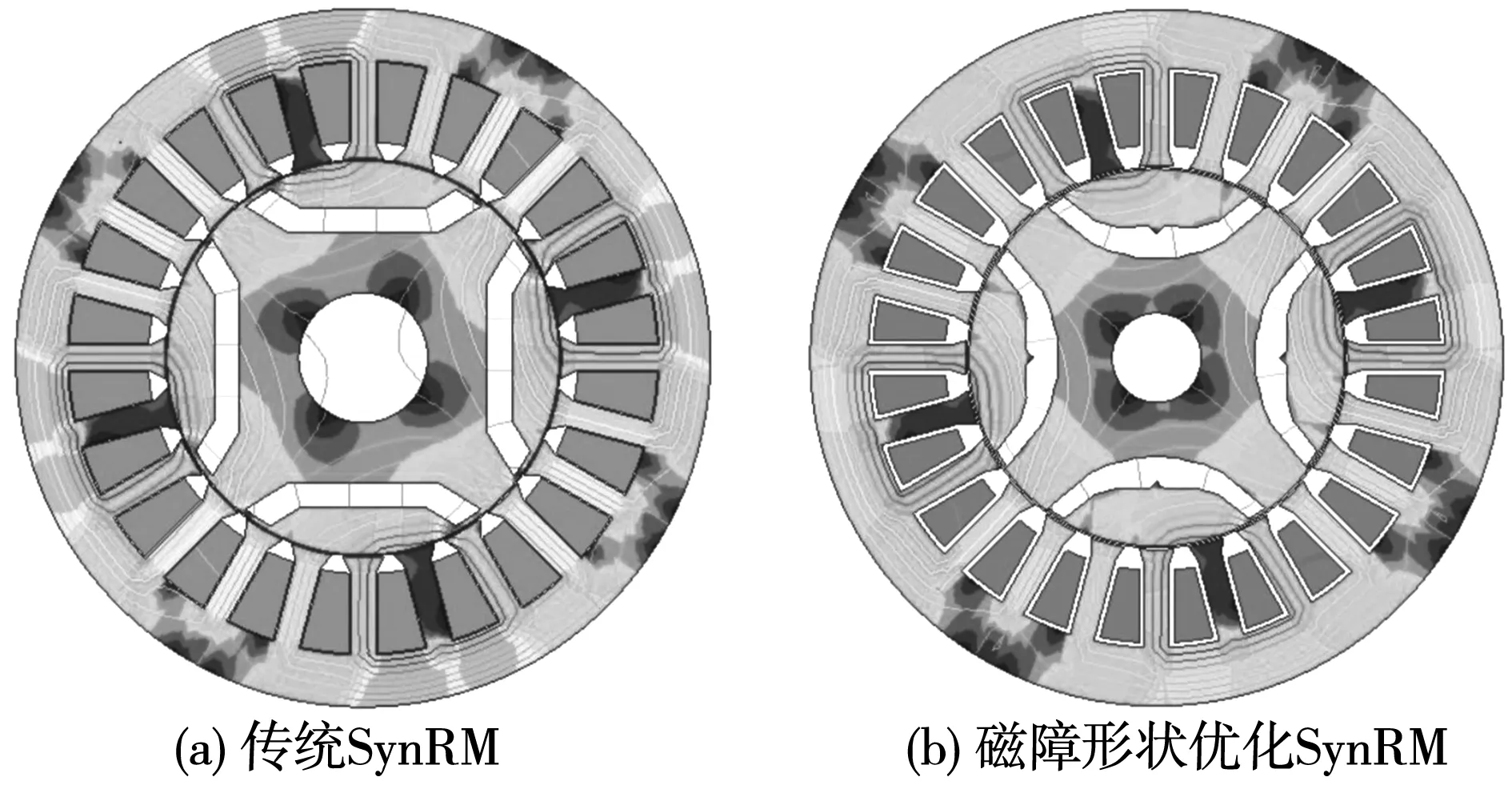
图8 一层磁障SynRMFig.8 One layer flux barrier SynRM

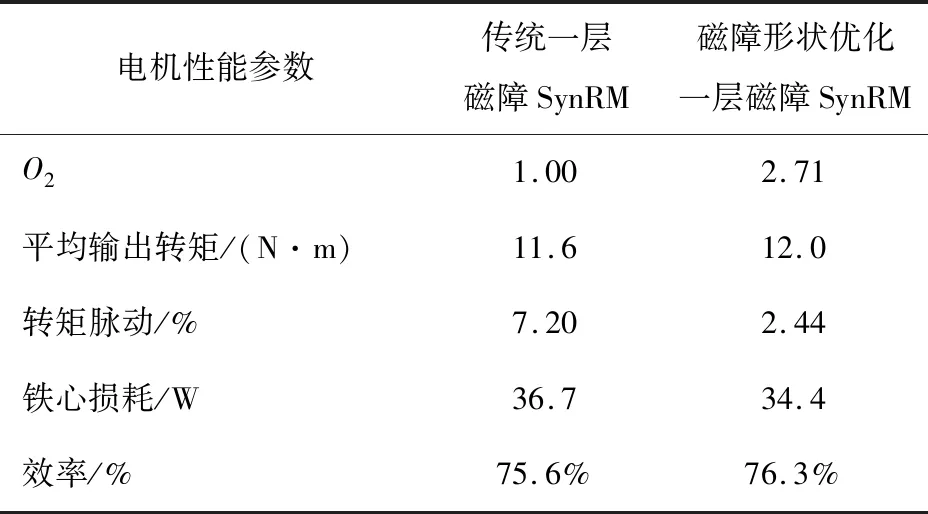
表2 额定转速下一层磁障SynRM性能对比Table 2 Performance comparison of one layer flux barrier SynRM under the rated speed

3.2 两层磁障SynRM性能对比

传统两层磁障SynRM结构如图9(a)所示，以12 A/mm2为最大电流密度工作点，对两层磁障SynRM的磁障形状进行优化，得到的磁障形状如图9(b)所示。表3为其与优化后的传统两层磁障电机主要性能对比，可以看出，对磁障形状进行优化能够有效降低电机的转矩脉动和铁心损耗，提高平均转矩和效率。

图9 两层磁障SynRMFig.9 Two layers flux barrier SynRM

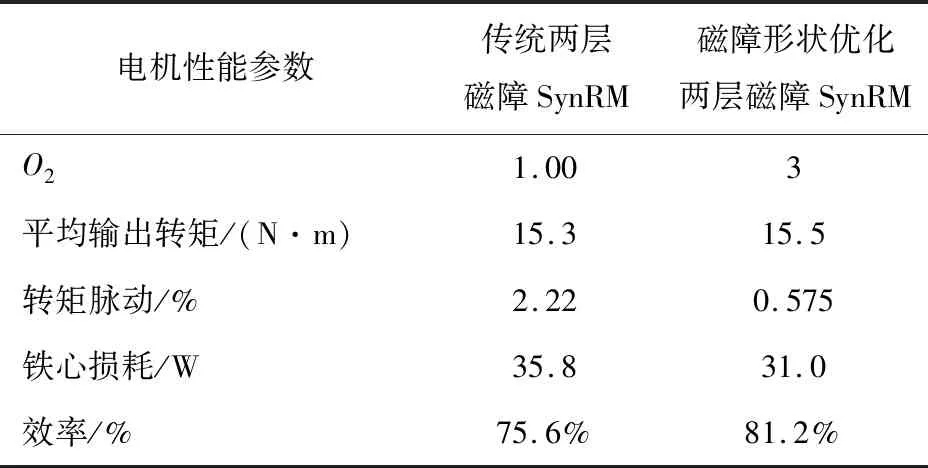
表3 额定转速下两层磁障SynRM性能对比Table 3 Performance comparison of two layers flux barrier SynRM under the rated speed

图10(a)为传统两层磁障SynRM交直轴电感随电流密度变化曲线图，图10(b)为磁障形状优化后的两层磁障SynRM交直轴电感随电流密度变化曲线。由图可知,低于额定电流密度6 A/mm2时，传统SynRM交直轴电感、交直轴电感差值以及凸极率均高于磁障形状优化后的两层磁障SynRM，主要原因在于对这两个电机进行优化时选择的工作点为峰值电流密度，未对额定电流密度下的性能进行考虑。而当电流密度高于6 A/mm2时，磁障形状优化使SynRM具有更好的性能。

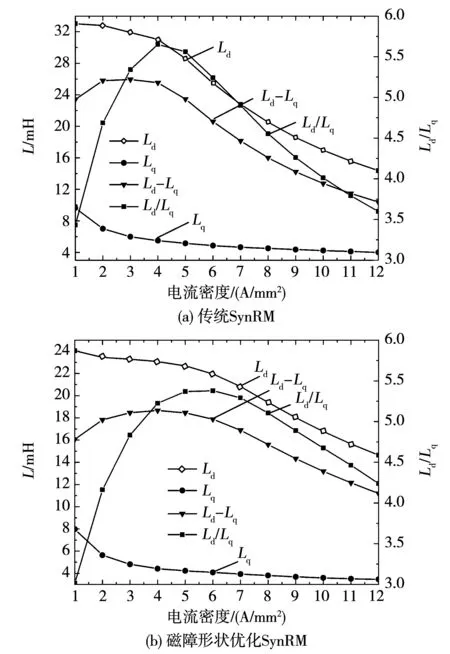
图10 电流密度与电感变化曲线Fig.10 Variation of inductance with the varied current density in SynRMs

图11为这两台电机的平均转矩和功率因数随电流密度变化的曲线。如图11(a)所示，两台电机的平均转矩随电流密度的增加逐渐增加，在电流密度较高时，磁障形状优化后的两层磁障SynRM的转矩上升较慢，而传统SynRM转矩上升较快。当电流密度小于12 A/mm2时，磁障形状优化后的两层磁障SynRM的平均转矩均高于传统两层磁障SynRM。如图11(b)所示，这两台电机的功率因数随电流密度增加先增加后降低，由于功率因数正比于凸极率，因此与凸极率变化趋势相同[25]。在达到额定电流密度之前，传统两层磁障SynRM的功率因数高于磁障形状优化后的两层磁障SynRM。当电流密度大于6 A/mm2时，相同电流密度下磁障形状优化后的两层磁障SynRM的功率因数高于传统两层磁障SynRM，且随电流密度增加，功率因数差值逐渐增大。

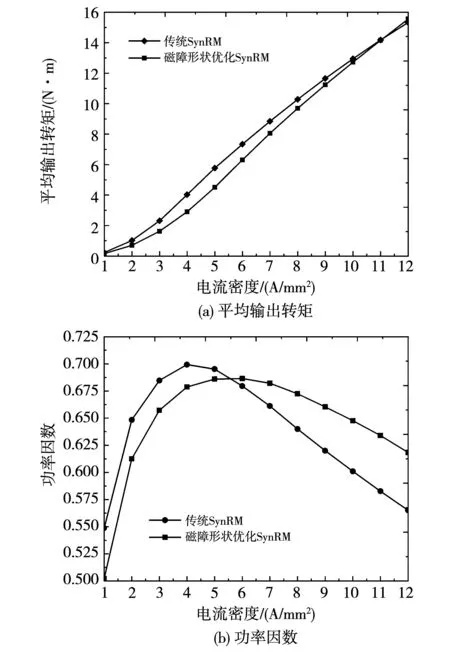
图11 SynRM平均输出转矩和功率因数与电流密度关系曲线Fig.11 Variation of average torque and power factor with the varied current density in SynRMs

图12为这两台电机在额定电流密度6 A/mm2及优化选取最大电流密度12 A/mm2时的输出转矩波形。由于SynRM的交直轴电感随电流变化较大，磁障形状优化后的SynRM在12 A/mm2时的输出转矩较高，且转矩脉动较低，在额定电流密度6 A/mm2时的转矩脉动较低，但输出转矩也低。

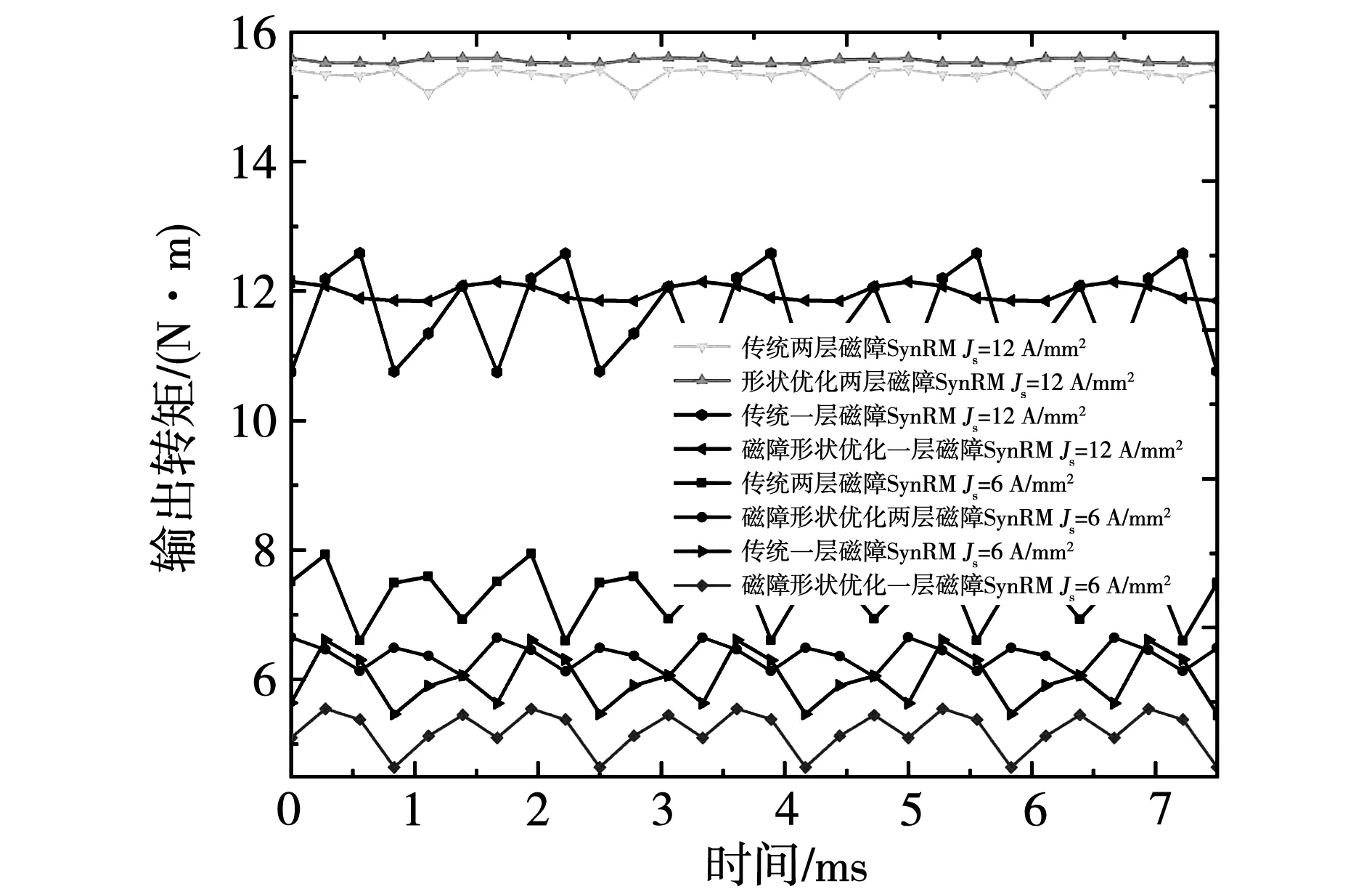
图12 SynRM转矩波形对比Fig.12 Comparison of torque in SynRMs

3.3 机械应力、应变分析

磁障形状优化后的同步磁阻电机对转子结构进行改变，需考虑在最高转速运行时所设计的转子结构是否可以承受最大应力、机械强度是否满足要求。图13、图14为对磁障形状进行优化后的SynRM在最高转速(6 000 r/min)下的机械应力与应变分析结果。

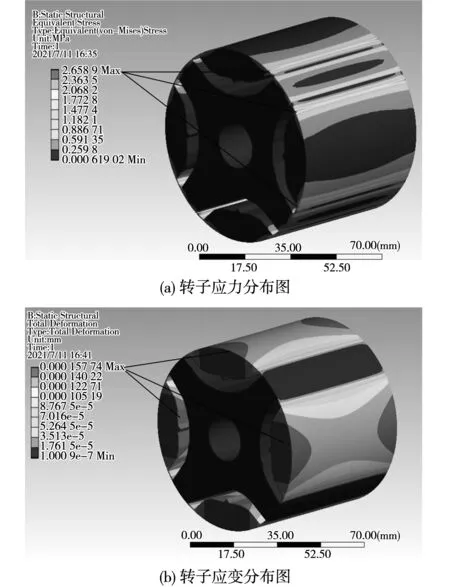
图13 磁障形状优化后的一层磁障SynRM应力分析Fig.13 Stress analysis of one layer flux barrier SynRM with optimized barrier shape

如图13(a)所示，一层磁障形状优化后的SynRM最大应力为2.66 MPa，如图13(b)所示，其最大应变为1.58 μm。最大应力出现在磁肋处，而最大应变出现在磁障的转子外侧处。传统一层磁障SynRM最大应力为1.43 MPa，最大应变为1.45 μm。如图14(a)所示，两层磁障形状优化后的SynRM最大应力为5.12 MPa，如图14(b)所示，最大应变为4.02 μm，其最大应变出现在两层磁障之间的位置。传统两层磁障SynRM最大应力为4.17 MPa，最大应变为2.89 μm。因此，优化后的SynRM在最大转速下的最大应力虽大于传统SynRM，但均小于所用硅钢片材料的最大允许抗拉强度，故磁障的变形是可以接受的。

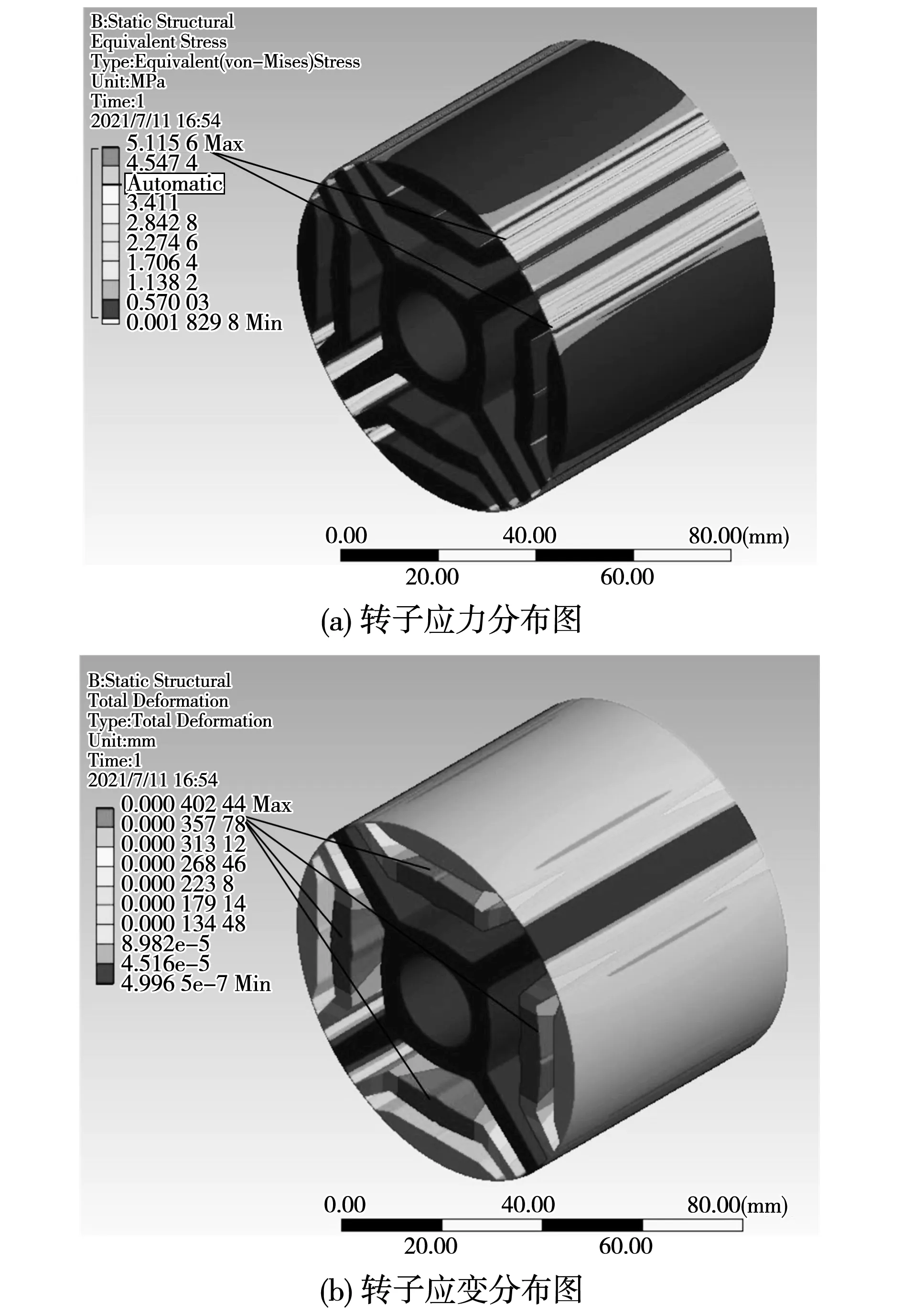
图14 磁障形状优化后的两层磁障SynRM应力分析Fig.14 Stress analysis of two layers flux barrier SynRM with optimized barrier shape

4 结 论

本文提出一种SynRM磁障形状设计及优化方法，应用分段线性插值法确定形成SynRM磁障的上下边界的关键点。以提高平均转矩和降低转矩脉动为目标，应用试验设计和全局优化相结合的方法对该电机进行优化。以传统SynRM为标准进行对比分析，对比结果表明，在选定的工作点下，对SynRM的磁障形状进行优化能够有效降低转矩脉动，提高平均转矩、功率因数和运行效率。然而，在优化时未考虑SynRM在其他工作状态下的性能，仍出现了传统SynRM的功率因数高于磁障形状优化后SynRM的情况，故在实际中需要考虑综合工况进行电机优化设计。对SynRM磁障形状进行优化，优化后的电机在最高转速下的最大应力在可接受范围内，电机转子不会变形，机械稳定性满足要求。