基于迁移学习的神经影像分析和阿尔茨海默病诊断
郝小可,李 想,阎 刚,王晓芳
(河北工业大学 人工智能与数据科学学院,天津 300401)
0 引言
阿尔茨海默病(Alzheimer′s Disease,AD)是一种迟发的神经退行性疾病。这种疾病通常见于65岁以上的人,它可以破坏患者的记忆能力和其他生理功能[1]。根据美国阿尔茨海默病协会最近的一项调查[2],AD已成为65岁以上美国老人的第五大死亡因素。目前,全球患有AD的人数达到4 700万。随着全球老龄化的发展,到2050年这一数字将超过1.31亿。全世界每33秒就有一个新确诊的AD病例。目前还没有治疗神经退行性疾病的方法,该疾病的诊断方法依赖于患者的临床症状和医生的经验[3],只有当病人有明显的症状时才能得到确认诊断。医生使用临床诊断方法诊断出来的病人往往处于疾病的晚期。因此设计一种有效早期诊断AD的方法,对病人的治疗和康复至关重要。
最近的研究表明一些神经影像技术已经被用于辅助计算机诊断疾病[4-6],包括磁共振图像(Magnetic Resonance Image,MRI)、扩散加权张量成像(Diffusion-weighted Tensor Imaging,DTI)和正电子发射断层扫描(Positron Emission Tomography,PET)。在这些新技术中,结构性磁共振成像(Structural Magnetic Resonance Imaging,SMRI)可以检测出大脑结构的异常[7]。例如,Lei等[5]提出了一个稀疏的自适应学习方法用于诊断神经退行性疾病,同时结合了局部保留投影方法和线性判别分析方法。Prashanth等[6]利用纹状体结合率(Striatal Binding Ratio,SBR)值作为特征输入,用于构建诊断帕金森病(Parkinson’s disease,PD)的支持向量机(Support Vector Machine,SVM)分类器。以上研究表明,神经影像数据可以对神经类退化疾病的诊断提供重要帮助。
一般来说,现有的诊断AD的方法集中在单个图谱上提取生物标志物。而从单一图谱得出的特征表示无法揭示不同人群(AD患者和正常对照(Normal Control,NC))之间的群体差异,也不能全面反映测试者的全局特征,这些情况会导致疾病诊断产生偏差[8]。实际上,大脑的结构和脑区之间的连接是复杂的,单一图谱的图像特征难以完全描述大脑的结构信息。相比之下,使用多图谱的方法可以捕捉到与疾病相关的鉴别特征和重要的结构性信息。目前已经有一些学者开始关注多图谱领域。例如,Min等[9]从不同图谱数据中提取到了丰富的特征信息。Liu等[10]提出了一种可以减少回归误差并去除测试者噪声特征的多图谱方法。这些研究都表明,使用多图谱数据可以提取与疾病相关的鉴别特征,从而极大地改善分类器的性能。
目前,大多数预测疾病的模型都是用单个中心的数据进行训练。单一中心的数据集通常比较小,因此无法训练出一个准确和稳定的疾病分类器。测试者较少的数据集由于样本量的限制,会导致训练后的分类器过拟合[11]。此外,模型在测试数据集上进行分类的准确率往往低于在训练数据集上分类的准确率,这个现象正是由于不同域的分布差异造成的。为了解决这些问题,一种直接的方法是将不同域的数据集直接合并,但是一些研究发现这种做法在脑部疾病分析中会使得实验产生矛盾甚至相反的结论。例如,Zhao等[12]发现AD患者的脑区整体连通性是低于正常人的,而Supekar等[13]却得出了相反的结论。造成这种现象的原因是多种的:首先,来自不同站点的样本具有不同的年龄和性别分布;其次,这些医学数据来自不同站点的不同设备,设备的型号和参数设置(头部线圈通道数和扫描时间)的不统一都会造成站点间样本数据分布的差异;此外,数据预处理方法的不统一也会造成这个问题。但是目前大多数的脑疾病分类方法都忽略了数据集之间的异质性问题。
为了解决不同数据集样本特征分布差异的问题,使用多站点数据间公共信息的域自适应方法应运而生。该方法的目的是为了提取域之间公共的信息特征。目前域自适应方法可以分为3种类型[14]:特征自适应、分类器自适应和深度自适应。1)特征自适应方法旨在根据两域的特征分布构建连接两域样本特征的桥梁。2)分类器自适应方法的目的是为了获得一个通用的分类器,该分类器对于源域和其他域的测试者都具有较好的识别性能。但是在分类器自适应的过程中产生的不正确的伪标签会极大地影响预测结果。3)深度自适应在目标域有标签时可以较好的工作,但是从目标域中获取大量的标签是一个具有挑战性的任务。此外,较小的样本规模很难训练出具有宽泛性的分类器。虽然跨域数据的特征分布具有差异,但是不同数据集同一类别的测试者的数据特征在空间分布上具有紧密联系。因此,本文关注基于特征的域自适应方法。在基于特征适应的迁移学习领域,一些研究者已经探索并取得了一些成果。例如,Gopalan等[15]在源域和目标域之间构建了采样测地流线来达到连接源域和目标域的目的。在此工作基础上Gong等[16]对模型进行了改进,通过构建一个内在的低维空间结构代替了高维投影矩阵,这个方法比原先的更加简单。Long等[17]构建了一个可以同时适应条件分布和边缘分布的模型,从而使特征有了新的表示。Jhuo等[18]提出了一个用于域适应的低秩重构模型,该模型将源域数据转化为过渡状态,从而使源域数据能够被目标域样本所表示。
如上所述,目前在计算机辅助诊断AD的研究中仍存在一些局限性。1)目前的研究大多只考虑单一图谱数据,不能捕捉到具有鉴别性和整体结构的特征信息。2)现有的方法往往忽略了不同域数据的异质性,这可能导致较差的分类性能。3)基于特征重构的域适应只是将源域映射到一个子空间,使两个域的数据可以相互表示,但是类信息没有被充分地利用,这就导致了域之间的分布差异问题不能很好地解决。为了处理这些问题,本文提出了一种基于多图谱的且针对类重构的域自适应AD分类方法。
本文提出的算法框架如图1所示。基于迁移学习的多图谱特征选择算法首先使用多图谱数据进行特征选择,然后通过特征自适应的方法来保留不同域之间的关联信息,最后使用多核支持向量机进行分类。与以前的工作相比,该模型融合了来自多个图谱的特征信息,保留与疾病相关的判别特征和整体的脑结构信息。通过低秩矩阵优化样本权重同时选择信息最丰富的特征。为了处理不同域分布差异产生的负面影响,模型在域适应过程中引入了特定类别的重构矩阵。最后在多中心阿尔茨海默病成像(Multi-Center Alzheimer’s Disease Imaging,MCADI)数据集和阿尔茨海默病神经影像学计划(Alzheimer′s Disease Neuroimaging Initiative,ADNI)数据集上对所提出的模型进行了评估。与其他域适应性迁移学习方法相比,实验结果表明本文提出的模型获得了最佳的分类精度。
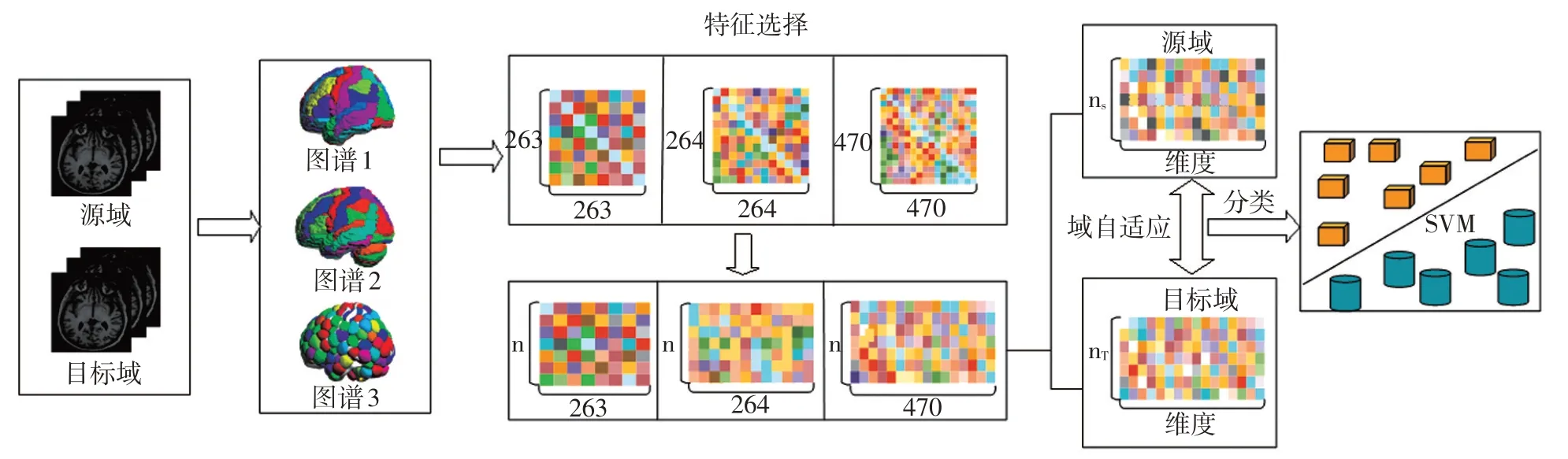
图1 基于迁移学习的神经影像特征选择算法框架Fig.1 Transfer learning-based neuroimaging feature selection algorithm framework
1 方法
1.1 多图谱特征选择
多图谱学习是对多个图谱数据同时进行学习,同时根据多图谱的样本权重信息进行多图谱的特征选择。
首先,模型进行特征提取。给定样本的M个图谱数据,即每个样本有M种大脑脑区划分形式,通过使用皮尔森相关系数计算任意2个脑区波形信号的相关性,然后使用一阶邻域聚合的方式进行特征表示。一阶邻域聚合的目标公式如下:

式中:O′1为第n个脑区所有连接强度之和;a1n为第1个脑区和第n个脑区之间的连接强度,将任意脑区所有连接强度之和作为该脑区的特征,最终一个样本的特征由其对应的O′1、O′2、…O′n组成。
接着采用基于权重诱导低秩学习的多图谱特征选择方法进行特征选择。表示第m个图谱的第i个样本,由该图谱上的每个样本所有脑区对应的一阶邻域聚合特征组成,yi是第i个样本的标签信息。最终的目标公式如下所示。

式中:N为样本个数;M为图谱数目;βm为第m个图谱的特征选择向量;wm i为第m个图谱上第i个样本的权重,任意一个样本权重wim都是大于0的。W∈RN×M为权重矩阵,其元素分别由不同图谱的样本权重构成。λM为约束图谱特征稀疏的正则化参数,λR为约束多图谱关联的正则化参数。
1.2 特定类别的域自适应
在机器学习问题中,通常在同一个数据集上进行训练集和测试集的划分。然而在现实世界中,由于数据集之间不满足同分布基本假设,在一个数据集上训练得到的分类器在其他的数据集上进行分类的准确率往往会有较大程度的下降。基于域自适应的迁移学习的目的是为了得到适用于不同数据集的普适性分类器。本文把源域表示为XS,目标域表示为XT,源域和目标域的数据均通过1.1节中的算法进行多图谱特征提取。由于源域和目标域的数据空间和维度不相同,研究者通常将2个域的数据映射到公共子空间中进行分布对齐。本文提出的方法将源域和目标域数据通过投影矩阵P投影到公共子空间后,通过重构矩阵Z来实现2个域样本的相互表示。接着利用标签信息,只希望源域和目标域中相同类别的样本之间可以实现相互表示,而不同类别之间的相互表示将被当作误差。本文所提出的迁移学习的模型框架见于图2。

图2 迁移学习框架Fig.2 Transfer learning framework
图2中上下两部分代表2个域,其中源域中的深蓝色图案和目标域中的浅蓝色图案属于同一类c1样本,源域中的黄色图案和目标域中的橙色图案属于c2类样本。Z为重构矩阵,其中Z的下标表示源域样本的类别,上标表示目标域样本的类别。在域自适应过程中,本文希望源域中的c1类样本可以和目标域中的c1类样本通过重构矩阵Z11构建连接;源域中的c2类样本可以和目标域中的c2类样本通过重构矩阵Z22构建连接。此外,源域中的c1类样本与目标域中的c2类样本构建的连接被视为误差;同样地,源域中的c2类样本与目标域中的c1类样本构建的连接也被视为误差。即图中的Z12和Z21两者表示的是2个误差项的重构矩阵。
依靠类别的域自适应方法的目标函数见公式(3):
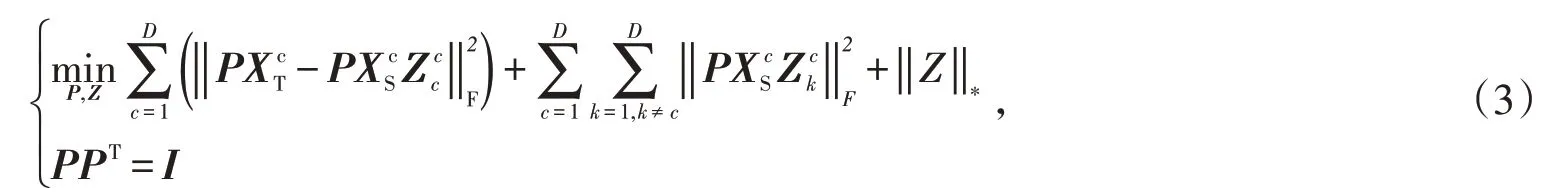
式中:PPT=I是用来得到共享投影矩阵P的非平凡解;PXSZ表示经过投影和重构的源域数据;而代表源域的c类样本在和目标域的该类样本进行相互表示时产生的误差;样本类别的数目为D;‖Z‖*是核范数,用来近似替代Z的低秩;为源域中的c类样本被目标域的k类样本表示,即该项为误差项。
通过多图谱特征选择方法可以保留不同图谱中与致病最为相关的特征,然后使用域自适应的方法对源域和目标域的样本进行迁移学习,从而消除不同域之间的分布差异。与传统的直接混合数据集的方法不同,本文提出的多图谱迁移学习模型能够同时结合多图谱和域自适应算法来改善分类器的性能。
1.3 函数优化
公式(3)的优化是凸函数优化问题,可以使用增广拉格朗日函数法(Augmented Lagrangian Method,ALM)来解决。引入辅助变量J和F,式(3)可以变化为下列形式:

将公式(4)变为增广拉格朗日的形式:
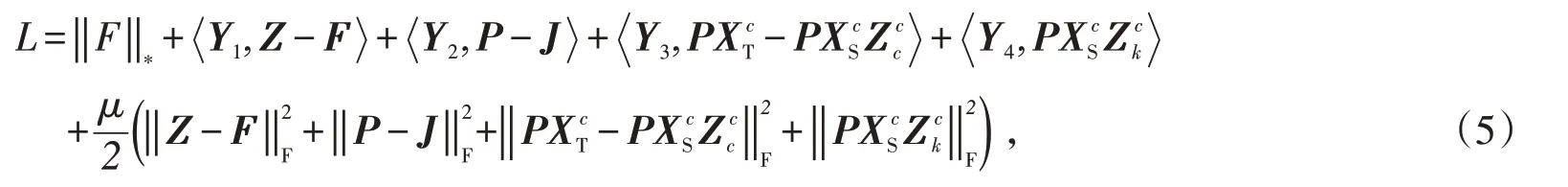
式中:Y1、Y2、Y3和Y4是拉格朗日乘子,μ是惩罚项的参数且μ>0。本文通过固定其他变量来迭代优化一个变量,在t+1(t>0)次迭代后求得解。
在t+1次迭代,通过式(6)~式(10)求解。
1)更新J:固定其他变量来更新J

2)更新F:固定其他变量来更新F
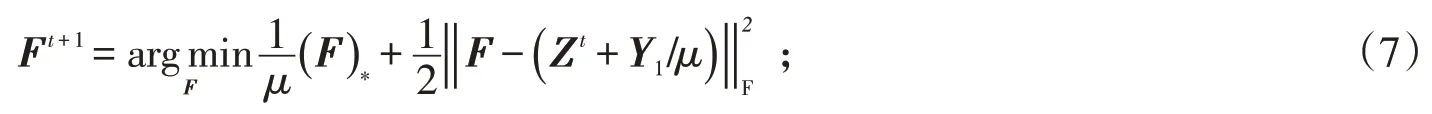
3)更新Z:固定其他变量来更新Z

4)更新P:固定其他变量来更新P

5)更新乘子以及参数:

具体的迭代更新步骤见算法1。

输1:入:源域样本XS和目标域样本XT初始化:添加辅助变量J和F,添加乘子以及参数2:while不收敛do 3:更新J:固定F、Z和P,公式(6)可以通过奇异值收缩法求解4:更新F:固定J、Z和P,公式(7)可以通过奇异值收缩法求解5:更新Z:固定J、F和P,公式(8)求解可得Z 6:更新P:固定J、F和Z,公式(9)求解可得P 7:更新乘子Y1、Y2和Y3 Y1=Y1+μ( )Z-F Y2=Y2+μ( )P-J Y3=Y3+μ( )PXc T-PXc SZc c Y4=Y4+μ(PXc SZc k)8:更新参数μ μ=min( )μ,μmax 9:检查收敛性end while输出:重构矩阵Z和投影矩阵P
2 实验数据与结果分析
2.1 评估参数
对于疾病二分类问题,通常考虑3个指标数据:精度(Accuracy,ACC)、敏感度(Sensitivity,SEN)、特异性(Specificity,SPE)。这些性能指标均由模型给出的标签预测值和真实值计算得出。为了方便计算这些性能指标,在这里引入混淆矩阵,见表1。
ACC是最为广泛使用的性能评估指标,它指的是所有预测正确的样本占全部样本的比例,计算方法见公式(11):
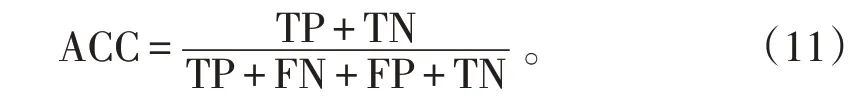

表1 混淆矩阵Tab.1 Confusion matrix
但是在医学应用场景中,尤其是在数据比例不平衡的情况下,只关注预测正确的结果会产生一定的误导性,例如把病人误诊为正常人是对测试者极大的不利。因此在实际情况下我们需要更有效的性能指标来全面地评估疾病分类结果。
SEN表示预测正确的阳性测试者占实际阳性测试者的比例,计算公式见下:

该指标越高,表示越多的阳性患者得到了确诊,即漏诊率越低。
SPE表示预测正确的阴性测试者占实际阴性测试者的比例。计算公式如下:

该指标越高表示越多的阴性测试者得到了正确的鉴别,即误诊率越低。
2.2 实验数据
本文实验数据来自MCADI和ADNI(http://www.loni.ucla.edu/ADNI)。ADNI标准数据集共有103个测试者,其中包含51名AD患者,52名NC。MCADI数据集包含467个测试者,其中包含252名AD患者和215名NC。MCADI数据集中每个被试均有3种图谱数据,包括Brainnetome图谱、Power图谱和Willard图谱。以上所有被试的图像都需要通过预处理才能得到相应的信号值或者特征值。
2.3 实验设置
为了验证本文提出的多图谱迁移学习方法的有效性,实验采用同类文章[11,19]所使用的5折交叉验证方法来评估本文提出算法的性能。具体来说,对于分类实验,将每个域的样本随机分为5个子集,依次选择目标域的4个子集加上整个源域作为训练集,剩下的1个目标域子集作为测试集。这样保证了在交叉验证中测试集的数据不会出现在训练集里。同时为了验证提出方法的鲁棒性,接下来交换源域和目标域。换句话说,原先作为源域的数据集作为目标域,原先当作目标域的数据集作为源域。同样地采用5折交叉验证方法来评估模型的鲁棒性。计算5次实验的平均精度、平均敏感度、平均特异性三个指标来评价各个方法的性能。
此外实验中需要使用支持向量机的分类方法(Library for Support Vector Machine,LIBSVM)工具实现。而且所有使用支持向量机分类的方法都采用线性核,参数依照系统默认值进行设定。
2.4 实验结果
为了验证本文使用的多图谱算法是否助于提高疾病分类性能,本文将提出的多图谱算法与使用单图谱、双图谱组合的特征选择方法进行对比。为了验证文本提出的迁移学习对于解决跨域问题的效果,本文同时使用传统支持向量机的方法(即未进行迁移学习的方法,用Baseline来表示)和其他迁移学习模型与本文提出的方法进行比较。
图3和图4是文中提出的方法在单图谱和双图谱上实验结果的对比,其中单图谱包括Brainnetome图谱、Power图谱和Willard图谱。双图谱方法为3个图谱排列组合构成的3个双图谱。最后为本文提出的3个图谱均使用的多图谱特征选择算法。

图3 不同图谱ADNI到MCADI的迁移结果Fig.3 Transfer results of different templates from ADNI to MCADI

图4 不同图谱MCADI到ADNI的迁移结果Fig.4 Transfer results of different templates from MCADI to ADNI
表2和表3展示了本文提出的方法与传统机器学习方法以及其他迁移学习方法的实验结果对比。基准方法(Baseline)是传统的支持向量机分类方法,也即未进行域自适应的方法。Geodesic flow kernel(GFK)[16]首先在源域和目标域之间构建一条测地线,通过测地线中集成的无数个子空间来一步步实现消除域间差异。Joint distribution adaptation(JDA)[17]通过同时调整源域和目标域的条件分布和边缘分布来实现联合分布的自适应。Label disentangled analysis(LDA)[19]是一种无监督自适应方法,该方法不是从标签层面来进行特征分布的对齐,而是去除部分标签信息但保留域间共享的标签信息,然后交叉对齐特征和标签进行数据的分类。表中的所有实验数据都是经过5折交叉验证取平均值后得到的。

表2 ADNI向MCADI迁移不同方法结果对比Tab.2 Result of different methods from ADNI to MCADI
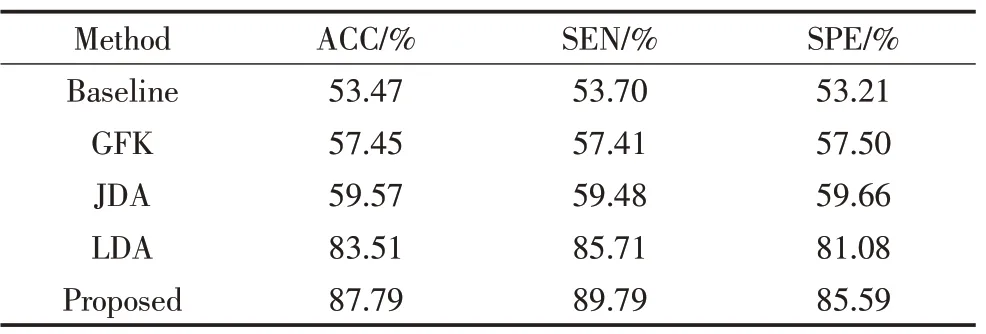
表3 MCADI向ADNI迁移不同方法结果对比Tab.3 Result of different methods from MCADI to ADNI
图3和图4展示了不同图谱数量组合,本文提出的基于迁移学习的多图谱特征选择算法用于AD分类的结果。图3中的实验将MCADI数据集作为源域,ADNI数据集作为目标域。图4中的其他实验条件和图3设置相同,不同之处在于把ADNI数据集作为源域,把MCADI数据集作为目标域。
从图3和图4的实验结果来看,使用双图谱的结果均优于使用单一图谱的结果,而使用全部图谱数据的算法性能最优。
表2和表3展示了不同的迁移学习方法在该数据集上的实验结果,2个表的实验设置差别体现在源域和目标域选择的不同。
从表2和表3中可以看到,不论是哪一种迁移方向,本文提出的方法的准确率是最高的,同时该方法的敏感度和特异性均是最高的,说明该方法对于AD具有较低的误诊率和漏诊率。此外所有使用迁移学习方法的准确率均高于Baseline方法,这证明了迁移学习有助于解决跨域分类问题。
为了进一步验证本文提出的依靠类别进行域自适应的算法有助于减少域之间的分布差异,针对是否利用类信息开展消融实验。具体来说,在公共子空间进行特征对齐时,不仅是同类样本之间进行特征对齐,不同类样本之间也会进行该步骤。同样地,该方法也进行了2组实验,表4展示了该方法在跨域数据集上的实验结果。
从表4可以看出,在域自适应过程中去除类信息后,2组实验的准确率在80.00%附近。将该实验结果对比表2和表3中的实验结果发现,未利用标签信息进行域自适应的算法准确率相比本文提出的算法准确率有着较大幅度下降。这表明了本文提出的依靠类别进行域自适应的算法有助于减少域之间的分布差异。
为了验证不同图谱对病变脑区的敏感程度不同,将1.1节中的多图谱特征选择算法用于探究不同图谱下患者大脑异常脑区。
在图5中,展示了3个图谱在不同平面上的致病脑区分布,其中每一列对应一个图谱,3个图谱分别为Brainnetome图谱、Power图谱和Willard图谱。由图5可以看出,从每个图谱中获得的感兴趣脑区位置在大脑各个平面中并不完全一致,这表明不同图谱对病变脑区的敏感程度不同,这也表明了使用多图谱数据的必要性。
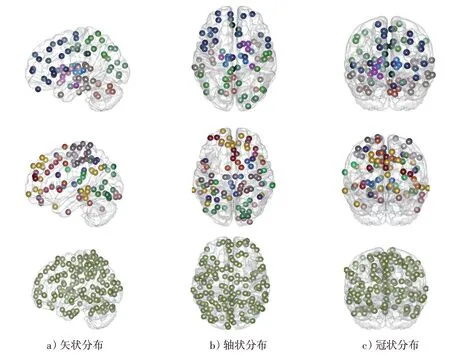
图5 3个图谱在不同平面的大脑节点分布图Fig.5 The distribution of brain nodes on different planes of the three templates

表4 消融实验结果Tab.4 Results of ablation experiments
3 结语
为了充分利用多图谱数据间丰富的互补信息,本文提出了一种基于迁移学习的多图谱特征选择算法,使用样本权重指导图谱数据进行特征选择。将进行特征选择后的数据开展迁移学习,将源域和目标域数据投影到公共子空间中使得源域和目标域的样本可以通过重构矩阵进行表示,此过程仅需要两域中同类别的样本进行迁移而不同类别之间的表示被视为误差。最后的分类实验结果证实了该算法的有效性。
今后的研究将从以下2个方面开展:1)本文只采用了2个域之间的迁移学习,而在临床上还存在其他的AD数据可以使用,可以考虑多个域数据同时进行迁移。2)数据集样本量不平衡时会对迁移效果产生影响,样本量较小的数据集在进行迁移时效果不稳定,针对这类情况该模型仍有改进的空间。

