基于小波和经验模态分解的气体泄漏声音端点检测算法
孙 静,聂士明,史宝军,4
(1.河北工业大学 省部共建电工装备可靠性与智能化国家重点实验室,天津 300401;2.河北工业大学 机械工程学院,天津 300401;3.河北省机器人感知与人机融合重点实验室,天津 300401;4.国家技术创新方法与实施工具工程技术研究中心,天津 300401)
0 引言
随着声音信息处理技术的发展,石化行业和其他复杂的高风险场所通过异常声音感知,预警危险事件的发生,而异常声音端点检测是异常声音感知的重要组成部分[1]。异常声音端点检测方法与语音信号的端点检测方法相似,常用的方法包含短时能量、短时过零率等,虽然在高信噪比及平稳噪声环境下,只使用短时能量或者短时过零率的方法检测效果较好,但在低信噪比环境下,单独的使用某一种方法可能达不到我们想要的效果。由于石化环境与采集设备等因素的影响,麦克风阵列采集的气体泄漏声音信号中一定含有噪声信号,为了减少后续对端点检测结果的影响,先对信号进行降噪处理,目的是提高端点检测的正确率。传统去噪方法是将带噪声音信号通过傅里叶变换[2]后再通过其逆变换得到原始的信号,但傅里叶变换不能较好的反映非平稳、非线性随机信号的特征,因此,相关学者开始研究小波[3]、经验模态分解(EMD,Empirical Mode Decomposition)[4]等适用于噪声环境复杂的非平稳、非线性声音信号的处理方法。
在低信噪比环境下,针对非平稳的随机信号,可以将短时能量和短时过零率结合,对采样的声音信号进行端点检测。唐骏龙等[5]提出了改进的语音端点检测中的能零比方法,虽然在信噪比大于等于0时检测准确,但是信噪比降低到0以下时,检测准确率下降到69.1%;汪鲁才等[6]应用小波去噪方法,对带噪信号进行降噪处理,采用端点检测模型对降噪信号进行端点检测,但是训练模型花费时间过长;韦莎丽等[7]采用EMD分解结合相关函数法的能零比算法对信号进行端点检测,但是相关函数法增加了能零比端点检测算法的计算复杂度和计算时间。
针对低信噪比下已有端点检测算法检测效果不理想以及检测所需时间长的问题,本文首先介绍了对声音检测信号进行小波变换和EMD分解的基本原理,以及信号降噪处理、特征分解与重构的有关算法;然后,给出了采用改进的门限值能零比方法,对气体泄漏信号进行端点检测的算法及其主要步骤;最后,搭建了简易的气体泄漏模拟实验平台,对改进的声音端点检测算法,进行了实验测试。
1 小波与经验模态分解
1.1 小波变换
小波变换的原理是信号函数f(t)与小波函数ψ(t)的内积[8],其中f(t)在平方可积空间,ψ(t)在时频域上具有良好的局部性质,如公式(1)所示:
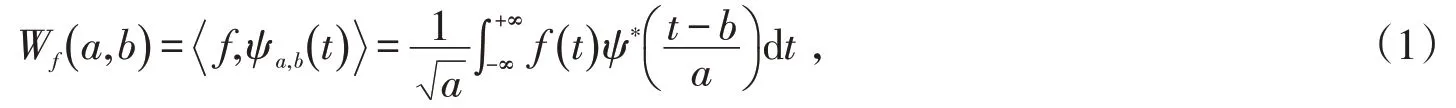
式中:〈*,*〉表示内积;a为尺度因子,a>0;b为位移因子;*表示复数共轭;小波变换的核函数是对母函数ψ(t)进行尺度伸缩a和时间平移b的结果。
一般当小波用于实际情况时,需要对尺度因子和位移因子进行离散,如公式(2)所示:

式中:k、q为整数,k>0;a0、b0为大于1的常数;a和b的选取与小波ψ(t)的具体形式有关。
离散化处理后的小波核函数如公式(3)所示:
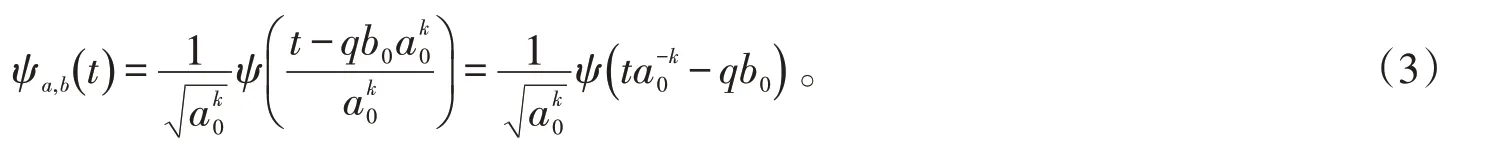
相应的离散小波变换如公式(4)所示:
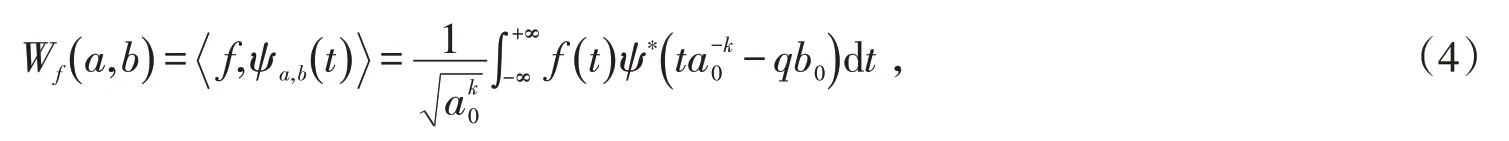
式中,当a0=2,b0=1时,为二进制离散小波变换,也称为二进小波。二进小波虽对尺度参数进行了离散化处理,但其在时间域上的平移仍是连续变化的,由于二进小波的时移共变性使得其在实际时间序列中被广泛应用,本文选用二进小波。
1.2 小波阈值去噪
小波基函数选择是小波阈值去噪的重要环节。常用的小波基函数有Haar小波、db(Daubechies)系列小波、Morlet小波、Mexican Hat小波、Meyer小波等[9]。通常通过正交性、对称性、紧支性、正则性和消失矩五种原则选择小波基函数。其中,正交性越好信号重构越精确;对称性存在,信号失真程度降低,运行速度相对较快;紧支撑性越好,能量越集中;正则性越好,重构信号平滑性越好;消失矩的存在可以保持良好的频域定域性。小波基的特性比较如表1所示。

表1 常用小波基特性比较Tab.1 Comparison of characteristics of common wavelet bases
通过表1的对比,本文小波基函数选择db系列小波,对采集的加噪信号进行小波阈值去噪。麦克风阵列采集的气体泄漏信号波形如图1a)所示,对原信号进行加噪,合成信噪比为0的信号,SNR=0时的波形图如图1b)所示,对信噪比为0的信号进行小波阈值去噪,去噪信号波形图如图2所示。
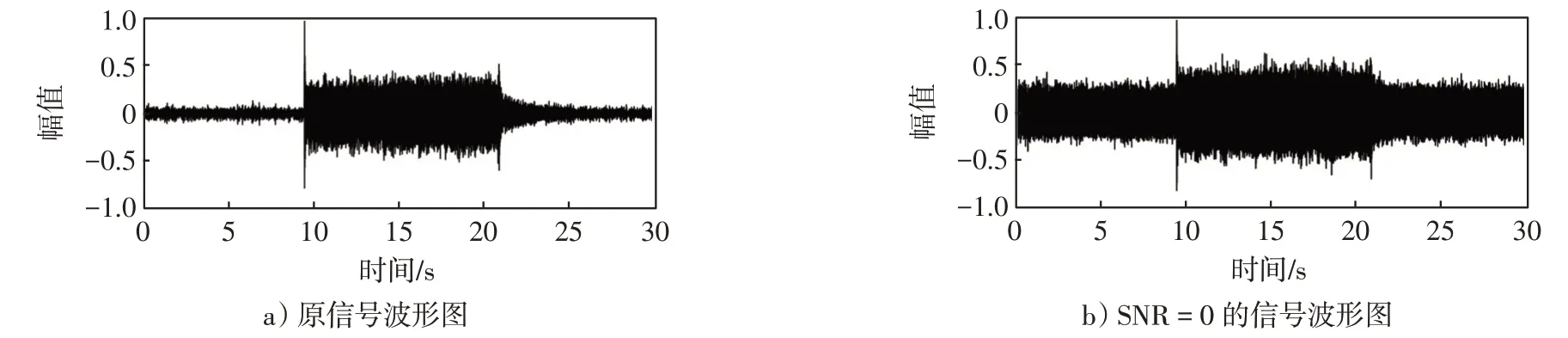
图1 原始信号与SNR=0的信号的波形图Fig.1 Waveform of the original signal and the signal with SNR=0
将麦克风阵列采集的泄漏信号图1a)看成纯净信号,通过图1b)与图2的对比可以看出,小波阈值去噪后的波形相对于加噪信号具有较好的去噪效果,但是与图1a)相比,仍存在噪声,所以需进行下一步的处理。
1.3 经验模态分解(EMD)算法
EMD算法是由美籍华裔科学家Huang博士1998年提出的一种处理非线性、非平稳信号的方法[4]。该算法的实质是将输入的复杂信号分解成若干个本征模态分量(IMF,Intrinsic Mode Function),而EMD提取IMF分量的分解过程如下:
1)找到泄漏信号x(n)所有的极大值点与极小值点,并通过差值的方法如三次样条拟合出由极大值组成的上包络线和极小值组成的下包络线,并对上下包络线求均值p(n);
2)在x(n)中减去平均值p(n),得到h(n),如公式(5)所示,并判断h(n)是否是一个IMF,判断条件:极值点的数目是否等于或者相差不超过一个过零点的数目;所形成的上下包络线是否关于时间轴局部对称。若不满足,则继续将h(n)作为待处理信号重复上述过程,直到找到满足判断条件的c1(n),如公式(6)所示:
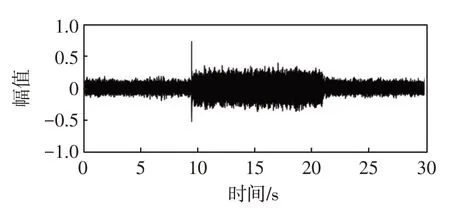
图2 小波阈值去噪的信号波形图Fig.2 Signal waveform of wavelet threshold denoising

3)得到一个IMF后,便可得到剩余序列r1(n),如公式(7)所示:

4)将r1(n)作为新的待处理信号,重复1)~3),可以获得所有的IMF分量:即c1(n),c2(n),…,cm(n),直到剩下残余分量rm(n)。判断是否是残余分量的停止判据为标准差Sd,Sd的值大部分取0.2~0.3,计算公式如公式(8)所示:

EMD算法的实质就是将x(n)分解成若干IMF即ci(n)和一个余量rm()n,如公式(9)所示:

对合成的信噪比(SNR)为0的信号进行小波阈值去噪,EMD分解去噪信号得到的各个IMF分量图如图3所示,分解出IMF1~IMF9和一个残余分量res。
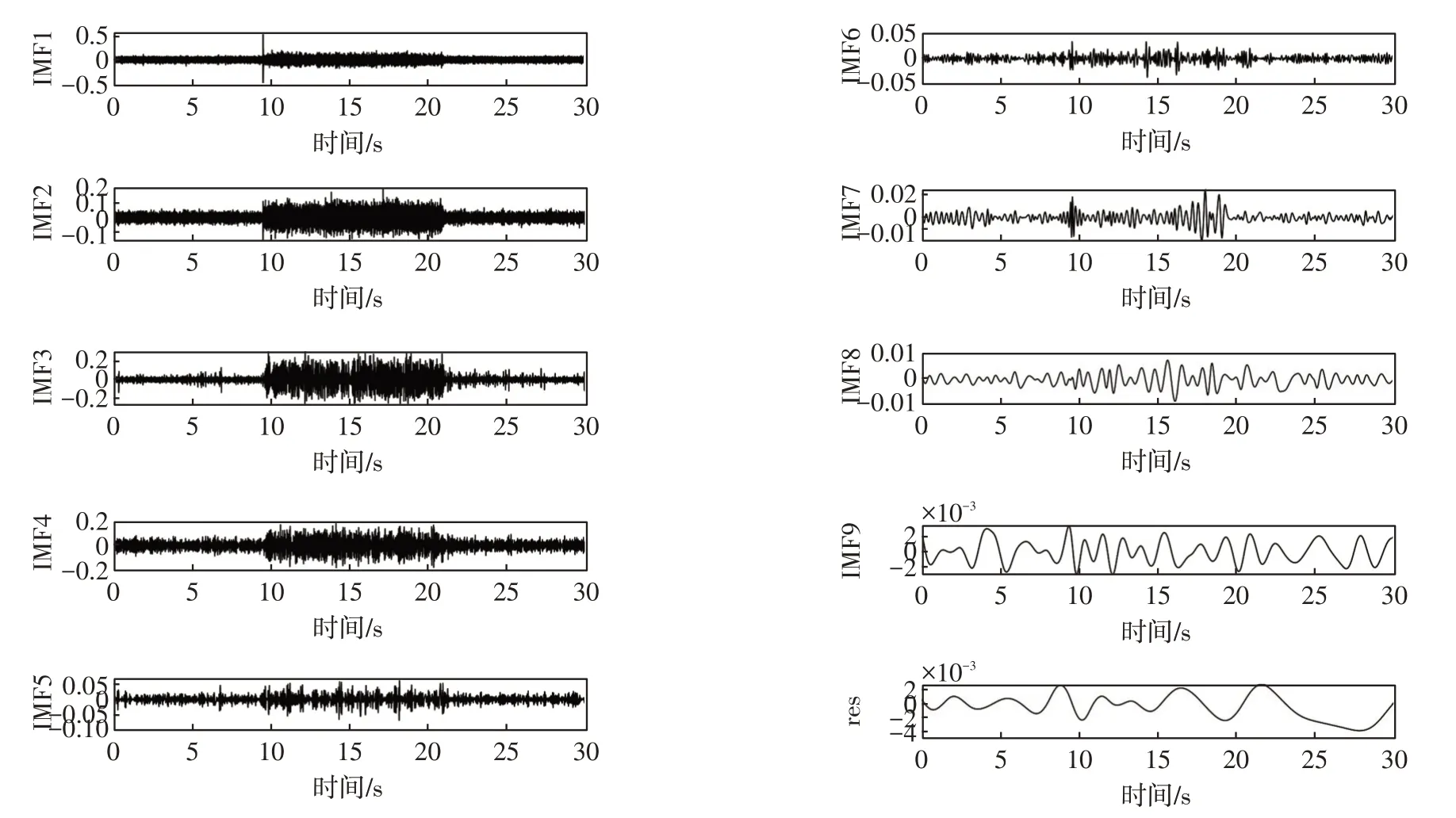
图3 经EMD分解去噪信号的IMF分量图Fig.3 IMF component diagram of denoising signal decomposed by EMD
从图3中可以看出小波去噪之后仍有噪声残留,且噪声主要分布在前两阶IMF分量中。采用文献[10]的方法,将选择的IMF分量进行重构,如图4所示。图4可以看出,相对于图2来说,信号的噪声进一步减少。重构后的信号好坏常用的判定指标为信噪比SNR。重构信号与小波阈值去噪信号的信噪比对比如表2所示。
通过表2可以看出,EMD重构后信号的信噪比相对于小波阈值去噪后的信号的信噪比提高了2.333 2。
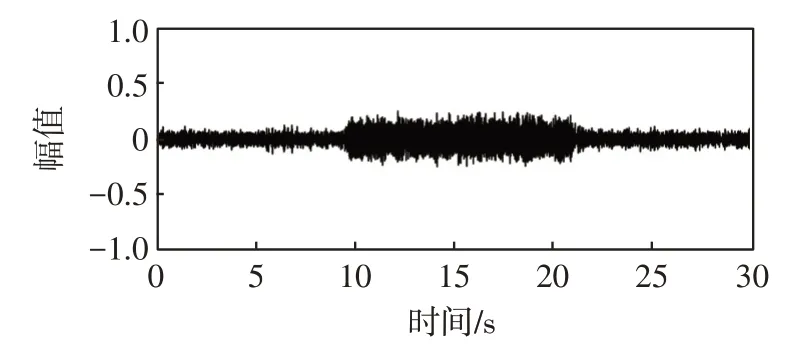
图4 重构信号波形图Fig.4 Reconstruction of signal waveforms
2 改进的自适应门限算法
2.1 传统能零比计算
麦克风阵列采集的泄漏信号x(n),通过分帧和加窗处理获得第i帧声音信号,表示为xi(n),其中每一帧的长度为N,则xi(n)如公式(10)所示:

表2 重构后的信号与小波阈值去噪后信号的信噪比对比表Tab.2 The SNR comparison table of the reconstructed signal and the wavelet threshold denoising signal
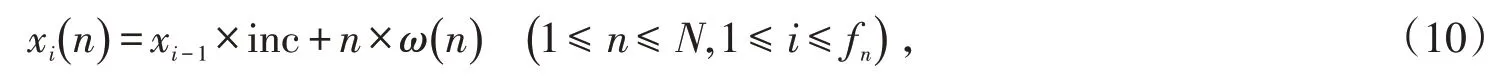
式中:ω(n)为窗函数;inc为帧移的长度。
第i帧泄漏声音序列xi(n)的短时能量[11]Ei如公式(11)所示:

短时过零率是指每帧中信号通过零值的次数[12]。泄漏信号xi(n)的短时过零率Zi如公式(12)所示:

式中,sgn[·]是符号函数,如公式(13)所示:

每帧的能零比EZi计算如公式(14)所示:

2.2 改进的自适应门限计算方法
在低信噪比环境下,传统的能零比端点检测算法的正确率很低,而且传统能零比算法中门限值的选取都是需要人为设定,最大门限值与最小门限值的选择会影响端点检测结果是否正确。本文在小波去噪的基础上,又引入EMD算法对去噪信号进行分解重构,对重构信号采用本文提出的自适应门限方法对泄漏信号进行端点检测。本文提出的自适应门限计算过程如下:
1)计算所有帧信号的的能零比值,找出最大能零比值与最小能零比值并求出所有帧信号的能零比值均值;
2)加权值P为2倍的均值与最大最小能零比值和的比值;
3)设置最小门限值:均值与最小能零比值之差;
4)设置最大门限值:最大能零比值与均值之差的P倍。
2.3 改进算法的步骤
1)对麦克风阵列采集的泄漏信号x(n)添加噪声库中的白噪声,生成SNR=0的合成噪声信号s(n)。
2)对s(n)进行预加重后的信号s′(n)通过小波阈值去噪得到S(n)。对S(n)进行EMD分解,采用文献[10]的方法,将剩余IMF重构。
3)将重构信号分帧加窗,采用文献[13]的短时能量计算公式计算每帧信号的短时能量,其中c为常数。
4)计算过零率之前,先进行中心截幅处理,如公式(15)所示,进而再计算过零率,如公式(16)所示:
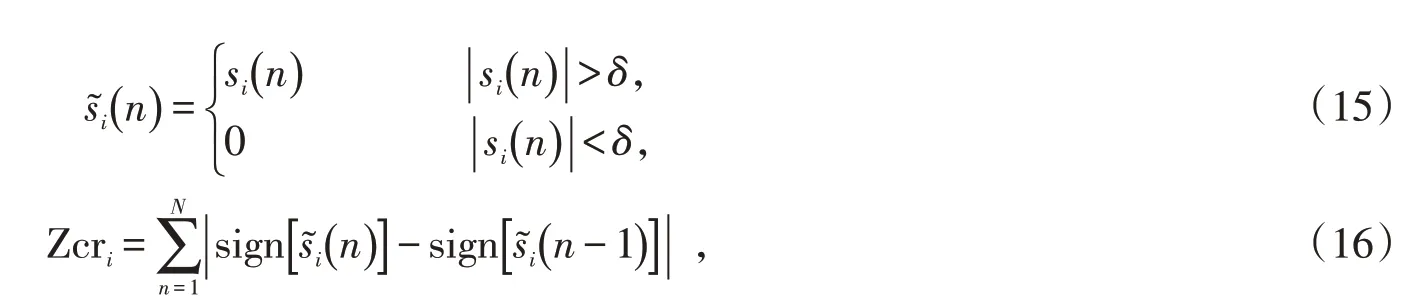
式中:si(n)为分帧加窗的信号;δ为一个很小的值;sign[·]为

计算每帧能零比值,如公式(18)所示:

式中:b为常数,取值较小,当过零率出现零时,防止溢出;Gi为每帧信号的短时能量。
5)计算重构信号所有帧的能零比值,相加并求均值E[E Zcr],求出最大能零比值EZcrmax与最小能零比值EZcrmin,如公式(19)~(21)所示:

式中,m重构信号分帧后的总帧数。
6)计算权值P,并求最大门限值ATmax与最小门限值ATmin,如公式(22)~(24)所示:
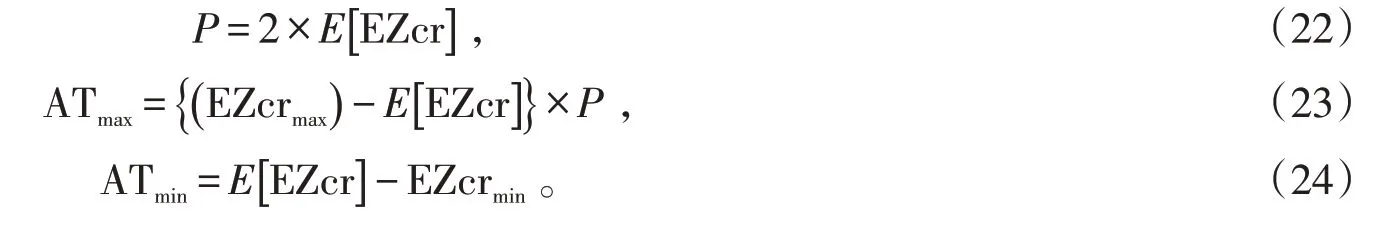
3 实验测试与讨论
通过麦克风阵列采集气体泄漏声音信号的实验原理如图5所示,简易实验平台如图6所示。实验使用的原始声音文件是在安静实验室下,采用Azure Kinect DK相机自带麦克风阵列所录制的,气体泄漏通过空气压缩泵进行模拟,噪声选自Noisex-92噪声数据库中的白噪声,采样时间为30 s,采用汉明窗,帧长为200,帧移为80。根据文献[14]可知,实际气体泄漏信号的有效信号的频率为几十到几百赫兹,在采样时,应该大于或等于有效信号频率的两倍,才可保证采样信号不失真,实验中采样频率为16 kHz,满足要求。
为验证泄漏源到麦克风阵列距离不同对端点检测结果的影响,实验中将麦克风阵列与泄漏源的距离设置为2 m、3 m、5 m和8 m,利用本文算法,得到端点检测精度与距离的关系,如图7所示。通过添加Noisex-92噪声库中的白噪声,生成信噪比为0的合成噪声泄漏声音信号,采用MATLAB软件对不同距离下的声音信号进行分析,实线代表起点,虚线代表止点。
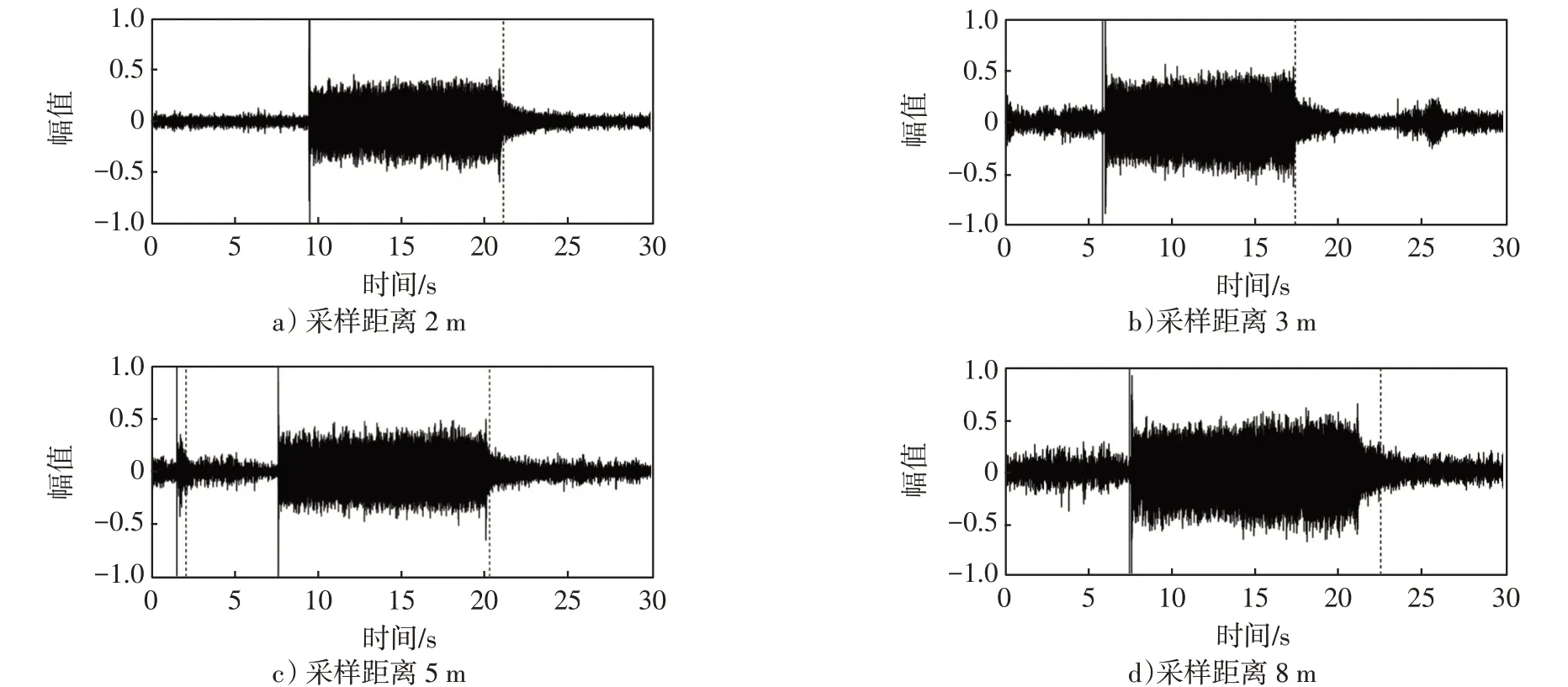
图7 采样距离为2 m、3 m、5 m、8 m时,端点检测结果Fig.7 When the sampling distance is 2 m,3 m,5 m,8 m,endpoint detection results
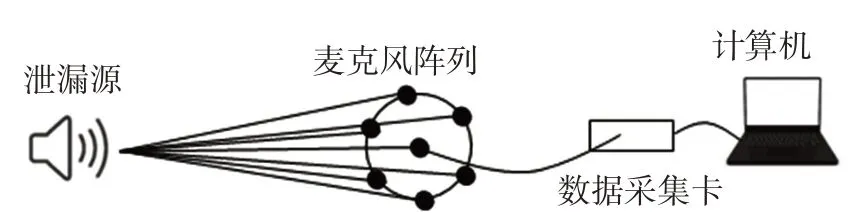
图5 实验原理图Fig.5 Experimental schematic diagram

图6 简易实验平台Fig.6 Simple experimental platform
从图7中能看出,随着采样距离的增加,本文的端点检测算法虽然起止点的判断误差在增大,但依旧能够判断出有效的声音段。由于实验中,空气压缩泵的开关需要人为控制,所以在每个采样距离中,空气压缩泵的开关时间不一样,所以有效的声音频段也不一样。为更直观的显示端点检测的误差,采用人工标记起止点的方法,并与MATLAB软件处理得到的起止点做比较,基于人工标记的起止点和MATLAB软件处理得到的起止点如表3所示。
从表3中可以看出,随着采样距离的增加,本文算法所得起止点的误差也有所增加。采样距离在5 m之内时,本文算法所得端点与人工标记端点的帧数基本接近;当采样距离大于5 m后,有效声音起止点与人工标记起止点相差较大。
为验证不同信噪比对端点检测结果的影响,实验中固定采样距离为2 m,通过添加噪声库中的白噪声,生成信噪比分别为-10、-5、5和10这4种不同信噪比的合成噪声泄漏信号,采用MATLAB软件对实验进行分析。根据图1a)麦克风阵列采集的信号波形图,基于人工标记,给出采集的信号的有效段起止点,即起点帧数为1 891,止点帧数为4 182。应用传统的能零比算法对合成的不同信噪比下的声音信号进行端点检测,传统能零比算法端点检测结果如图8所示。
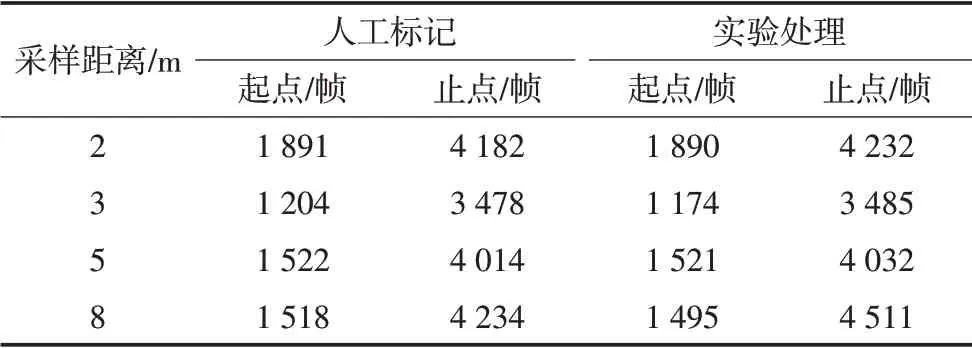
表3 基于人工标记和MATLAB软件处理得到的起止点对比Tab.3 The starting and ending points are compared based on manual marking and MATLAB software processing
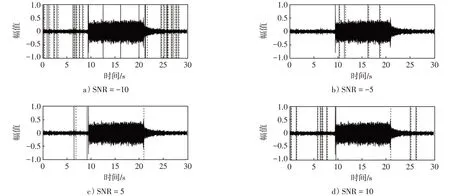
图8 SNR=-10、-5、5、10时,传统能零比端点检测结果Fig.8 When SNR=-10,-5,5,10,the traditional zero-ratio endpoint detection results
通过图8可以看出,在不作任何处理的情况下,传统的能零比算法在不同信噪比下端点检测的结果并不理想。当信噪比大于0时,从图中可以看出传统能零比算法虽然存在误判,但是也能将有效的声音频段提取出来;当信噪比小于0时,传统能零比算法不但存在误判,而且也没有正确的检测到有效频段。
为提高传统能零比算法的识别率,将EMD算法应用于能零比算法中,并应用此算法对合成的不同信噪比下的声音信号进行端点检测,基于EMD的能零比端点检测结果如图9所示。
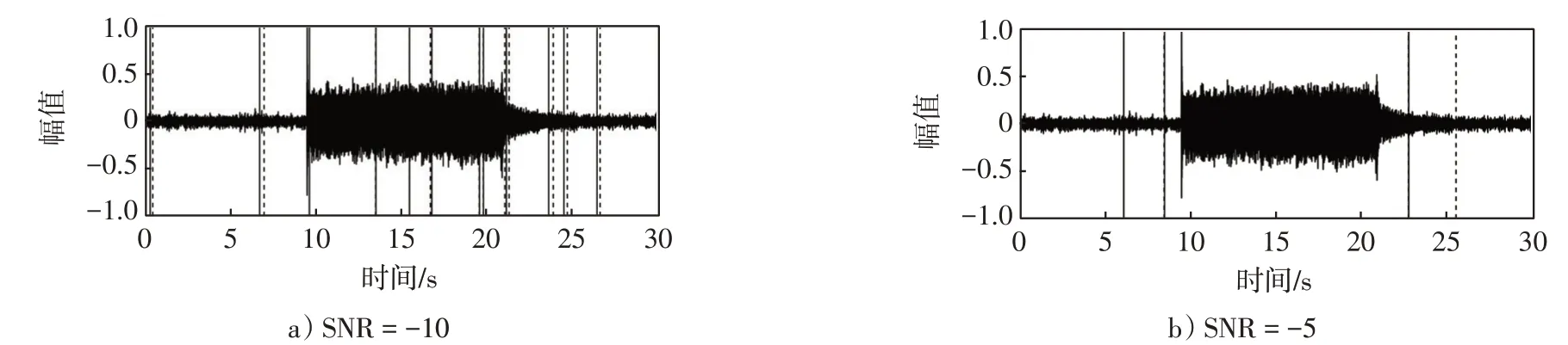

图9 SNR=-10、-5、5、10时,基于EMD的能零比端点检测结果Fig.9 When SNR=-10,-5,5,10,the detection results of energy zero ratio endpoint based on EMD
通过图9可以看出,在信噪比大于0时,基于EMD的能零比端点检测算法可以有效的检测到信号的端点;当信噪比小于0时,此算法不仅会降低检测正确率,而且还存在严重的误检现象,将无效段误判为有效段信号。基于EMD的能零比算法在不同信噪比下的端点检测起止点以及检测时间如表4所示。
从表4中可以看出,在信噪比大于0时,基于EMD的能零比端点检测算法也可以较好的检测出有效段信号且随着信噪比的提高,检测的起止点越来越接近人工标记的有效段的起止点;当信噪比小于0时,无法正确判断有效段信号的起止点;从表中也可以看出,随着信噪比的降低,基于EMD的能零比算法端点检测所需的时间也随之增加。
采用基于小波和EMD的改进门限的能零比算法,对合成的不同信噪比下的气体泄漏声音信号进行端点检测,端点检测结果如图10所示。
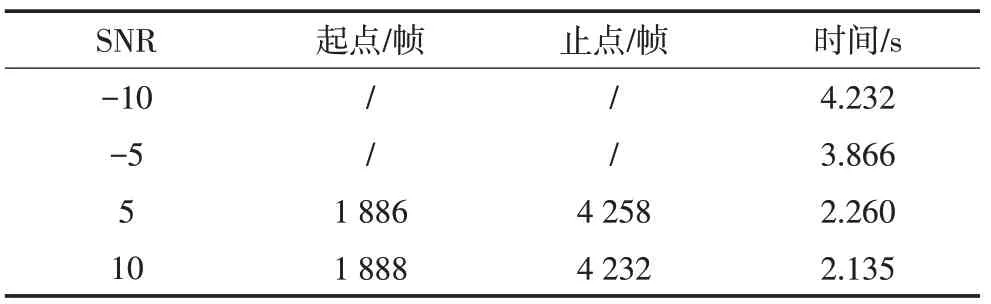
表4 基于EMD的能零比端检结果及时间Tab.4 Energy zero ratio end test results and time based on EMD

图10 SNR=-10、-5、5、10时,改进算法的端点检测结果Fig.10 When SNR=-10,-5,5,10,the endpoint detection result of the improved algorithm
通过图10可以看出,不论信噪比大于0还是小于等于0时,基于小波与EMD的能零比端点检测算法都可以较好的检测出起止点。改进门限的能零比算法在不同信噪比下的端点检测起止点以及检测时间如表5所示。
从表5可以看出,在信噪比为10时,检测的有效段起止点最接近人工标记的起止点;随着信噪比的降低,改进算法仍可以有效检测到有效段信号,且检测所需的时间随着信噪比的下降而增加。通过图9和图10的对比可以发现,在信噪比相对较高的情况下,两种算法都可以正确的检测到有效的声音信号段;当信噪比下降时,基于EMD的端点检测算法既无法有效检测出有效段,也存在误判现象,但改进的算法依旧可以准确的检测出泄漏声音的端点。对比表4与表5,相同信噪比下,改进算法比基于EMD算法所判断出的端点接近人工标记的端点,而且所用时间短。
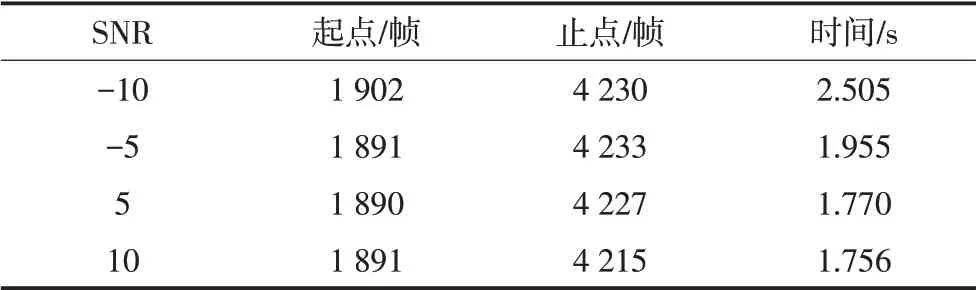
表5 改进算法端点检测结果及时间Tab.5 The result and time of endpoint detection were improved
4 结语
泄漏信号的端点检测结果直接影响后续的处理,而传统的能零比算法存在误判甚至无法检测到有效信号段的现象。由于石化场景环境复杂,在对泄漏信号进行端点检测之前,首先对泄漏信号进行降噪处理。本文利用小波阈值去噪,并结合EMD分解,提出一种改进门限的能零比气体泄漏声音端点检测算法。实验结果表明,随着距离的增大,本文算法的端点检测精度虽然降低,但却依旧可以检测出有效片段;与传统的能零比和基于EMD的能零比算法相比,本文提出的算法在低信噪比下不仅具有良好的稳定性,而且检测所用的时间也相对较少。
本文的研究工作可为危化品气体泄漏检测提供一种较好的泄漏声音检测算法,并为进一步开展危化品气体泄漏的远距离非接触式检测研究提供一定的基础。

