关于非齐次树指标马氏链随机矩阵的一个强偏差定理
金少华,王丽君,谭彦华
(河北工业大学 理学院,天津 300401)
0 引言
强偏差定理一直是国际概率论界研究的中心课题之一,对强偏差定理的研究不仅对概率论与随机过程自身的发展很有意义,而且在统计学中统计量的分析及排队论的逼近理论中有广泛应用。树模型近年来已引起物理学、概率论及信息论界的广泛兴趣。树指标随机过程已成为近年来发展起来的概率论的研究方向之一。科学家在研究杆状菌的分裂时,总结出杆状菌分裂的规律,即一个杆状菌在分裂时,从中间断开,这样就分裂成两个新杆状菌,这两个新的杆状菌为原来杆状菌的后代。如果把每一次分裂中的杆状菌看成一个顶点,那么杆状菌的分裂过程就可以抽象为一个二叉树结构。如果杆状菌分裂时受到周边环境的影响,这样杆状菌的分裂过程就可以抽象为一个随机环境中的二叉树模型,因此研究随机环境中树指标随机过程不仅具有理论意义,更具有应用价值[1]。文献[2]首先研究给出了二叉树有限状态分枝马氏链的随机序偶出现频率的强大数定律,之后研究给出了二叉树有限状态分枝马氏链函数的强大数定律,作为推论给出了二叉树有限状态分枝马氏链的Shannon-McMillan定理。Shi Zhiyan等[3]给出了m根Cayley树上m阶渐近奇偶马氏链的强大数定律。Huang Huilin等[4]研究给出了2根Cayley树上二重循环马氏链的渐近均分性。Tang Ying等[5]给出了齐次树指标渐近奇偶马氏链的强大数定律,并通过一个例子说明了所得结果的重要性。刘建国等[6]利用二元函数延迟平均的强极限定理和条件期望的平滑性,给出了可列马氏链状态出现频率延迟平均的强大数定律。文献[7]研究给出了齐次树指标马氏环境中的马尔科夫链的Shannon-McMillan定理。杨洁等[8]研究给出了关于齐次树指标马氏链的广义熵遍历定理。文献[9]研究给出了树指标马氏双链的Shannon-McMillan定理。文献[10]给出了连续状态非齐次马氏链多元函数的强大数定律。Yang Jie等[11]给出了非齐次马氏链广义样本相对熵的强大数定律。Shi Zhiyan等[12]给出了随机环境中Cayley树指标马氏链的Shannon-McMillan定理。文献[13]给出了马氏环境中树指标马氏链随机转移概率调和平均的强极限性质。文献[14]给出了2个渐近循环马尔科夫链之间相对熵密度率的强极限定理。文献[15]给出了关于树上m重非齐次马氏信源的一个小偏差定理。本文通过引入滑动相对熵的概念,研究给出了关于非齐次树指标马氏链的一个强偏差定理。
1 基本概念
设{Nn,n≥1}是一列正整数集,T是一个具有根顶点O的无限树,如果T的第n(n≥0)层上的每个顶点均与第n+1层上的Nn+1个顶点相邻,则称T为广义Bethe树或广义Cayley树。特别地,若对非负整数集N,用模m的同余关系对其进行分类得到如下模m的剩余类:

当n∈(i)时,令Nn+1∈αi(αi均为正整数且不同时为1),i=0,1,2,…,m-1,就得到了一类特殊的非齐次树Tα0,α1,…,αm-1。以下恒以T表示树Tα0,α1,…,αm-1,以S(t)表示顶点t的所有子代的子图,Ln表示第n(n≥0)层上所有顶点的子图。
定义1设{Ω,F,P}为一概率空间,{Xσ,σ∈T}为定义在该概率空间上并于字母集S={1 ,2,…,m}上取值的随机变量族,设

是S上一概率分布,而

是定义在S2上的随机矩阵列,如果∀t,si∈T满足si∧t≤1≤i≤n,有
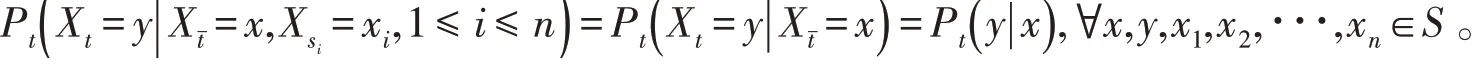
并且

则称{Xσ,σ∈T}为具有初始分布(1)与转移矩阵列(2)的在S上取值的树指标非齐次马氏链。则其联合分布为

设Q是可测空间(Ω,F)上另一概率测度,且随机变量关于Q独立,即存在S上的一列分布


设{al,l≥1}是一单调不减的非负整数数列,令
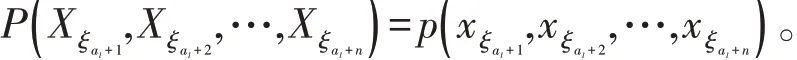
定义2设{Xσ,σ∈T}为具有初始分布(1)与转移矩阵列(2)的在S上取值的树指标非齐次马氏链,式(4)是给定的一列S上的分布。则称

与

分别为{Xσ,σ∈T}相对于独立测度Q的滑动似然比和滑动相对熵。
2 强偏差定理
引理1设{Xσ,σ∈T}是如前定义的树T上的非齐次马氏链,如前定义。设,对一切n≥1,取λξn,k使得

令

证由式(3),有

由式(10),有

令

则


由式(12)和式(13),有

定理1设{Xσ,σ∈T}为具有初始分布(1)与转移矩阵列(2)的在S上取值的树指标非齐次马氏链。pξn,k,λξn,k,Rn(ω)及R(ω)均如前定义。设k∈S,Sξal,n(k,ω)表示Xξal+1,Xξal+2,…,Xξal+n中状态k出现的次数,c为一非负常数,令
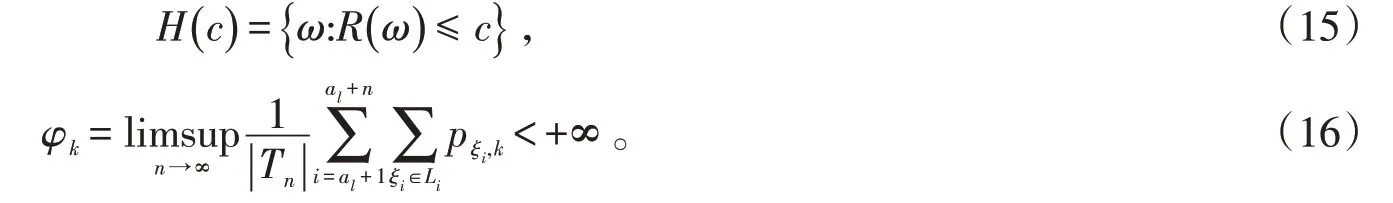
则

证由引理1及Doob鞅收敛定理知,存在集合A(λ),P(A(λ))=1,使得

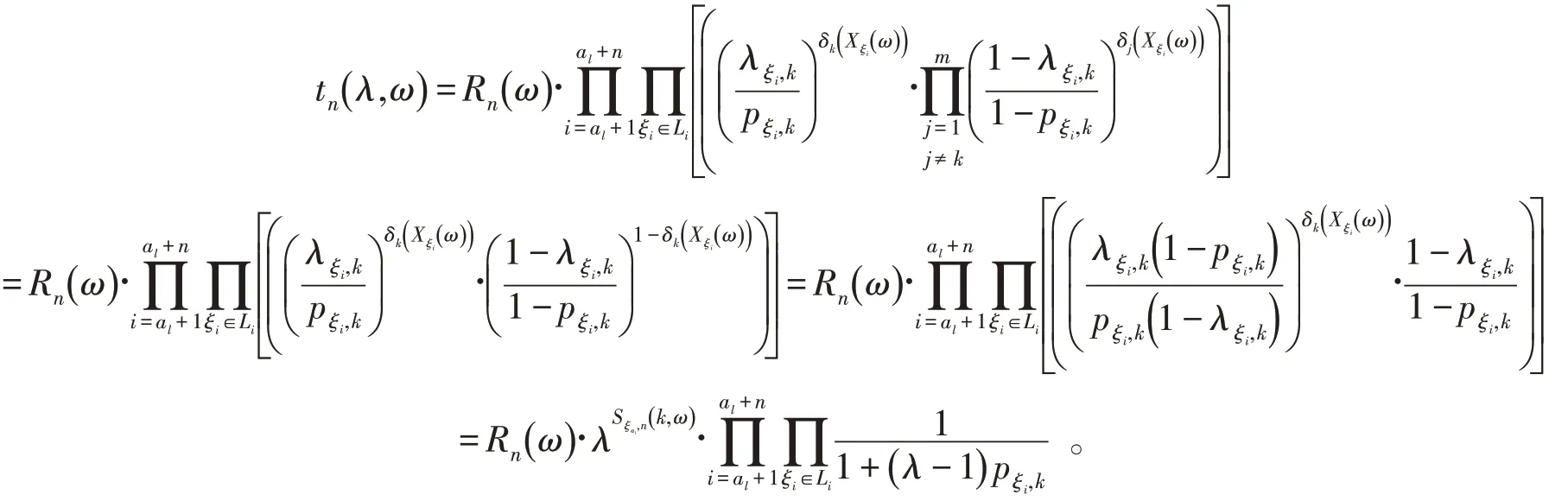
即

则由式(19)和式(20)有

由式(21)有

当λ>1时,将式(22)两端同除以lnλ,有

由式(23)与上极限的性质

及不等式

有

当c>0时,函数在处取得最小值,于是有


当c=0时,取正有理数λi(i=1,2,…),使得λi→1+(i→+∞),并令,则对一切自然数i,由式(24),有
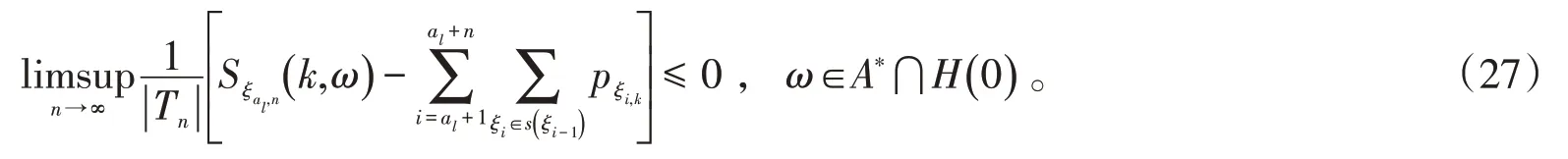
因为P(A*)=1,故由式(26)及式(27)知式(17)成立。
当0<λ<1时,将式(22)两端同除以lnλ,得
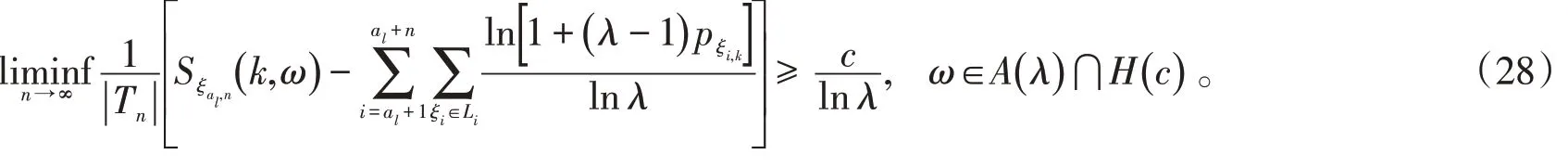
利用下极限的性质
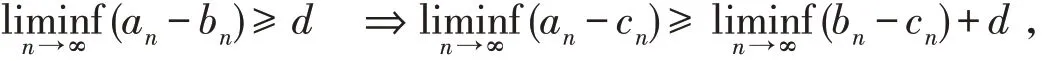
及不等式

由式(28)有
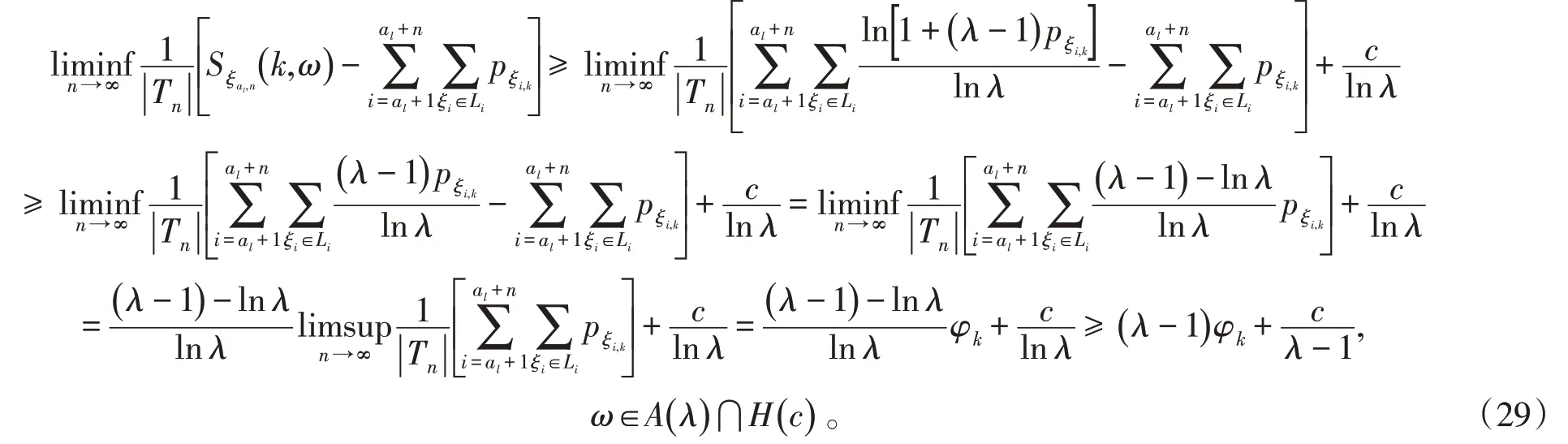
当c>0时,函数在处取得最大值,于是有


当c=0时,取正有理数λi(i=1,2,…),使得λi→1-(i→∞),并令,则对一切自然数i,由式(29),有

因为P(A*)=1,故由式(31)及式(32)知式(18)成立。
推论1设{Xσ,σ∈T}为具有初始分布(1)与转移矩阵列(2)的在S上取值的树指标非齐次马氏链。pξn,k,λξn,k,Rn(ω)及R(ω)均如前定义。设k∈S,Sξal,n(k,ω)表示Xξal+1,Xξal+2,…,Xξal+n中状态k出现的次数,令H(0)是满足下面条件(33)式和(34)式的点ω的集合:

则

证在式(17)和式(18)中令c=0,即得式(35)成立。

