基于车载LiDAR点云的杆状地物分类研究
董亚涵,李永强,李鹏鹏,范辉龙
(河南理工大学 测绘与国土信息工程学院,河南 焦作 454003)
杆状地物是城市道路场景中最为常见的公共设施,包括路灯、电线杆、广告牌及交通标示牌等,传统的杆状地物分类方法通常是使用全站仪、RTK等测量仪器对杆状地物位置进行实测后再进行编号标记,并结合AutoCAD及其他软件进行绘图,但由于传统方法采集的数据不完整、精度不高且人为干预严重,难以为智慧城市、道路建模及无人驾驶等新技术提供数据支持,车载LiDAR(Light Detection And Ranging)作为测绘领域的前沿技术之一,为城市空间信息的精确获取提供了强大的技术支持[1-2]。车载LiDAR在车辆行驶过程中获取道路两侧地物详尽的三维空间点云信息,相比于传统杆状地物测量方法具有明显优势,杆状地物的空间信息精确地表达在车载LiDAR点云数据中,为杆状地物的自动分类提供数据条件。
目前,针对点云中的杆状地物的分类提取研究,学者们开展了一系列工作并取得很多成果[3-18],但也存在各种局限性的问题,如只实现了行道树的特征矩阵构建与识别,对于相似性高的杆状地物如路灯与广告牌的分类并未涉及,本文通过提取杆状地物多种特征构建特征矩阵,并采用SVM分类算法建立分类模型,实现对车载点云数据中多种典型杆状地物的分类。
1 点云特征矩阵构建
1.1 顶部与杆部分离
杆状地物通常包括顶部和杆部两部分,如图1所示,行道树树冠与树干(图1(a))、路灯灯头与灯杆(图1(b))、标示牌牌与杆(图1(c)),电线杆包含两种:一种包含头部(图1(d)),一种不包含顶部(图1(e)),虚线框中为杆状地物顶部。相比于杆部,杆状地物顶部包含了更多特征,因此,先对杆状地物进行顶部与杆部分离,对于不包含顶部的电线杆,取其与电线连接处作为顶部。文献[19]采用自低而上的格网增长法进行行道树的冠干分离,但由于路灯广告牌等地物没有明显的格网增加难以建立分割阈值,本文将对格网数目增加的判断修改为对点云跨度的变化判断[3],即对单个杆状地物从底部开始向上以0.2 m距离间隔进行搜索,当点云跨度超过阈值,则判断搜索到了头与杆部的分界。
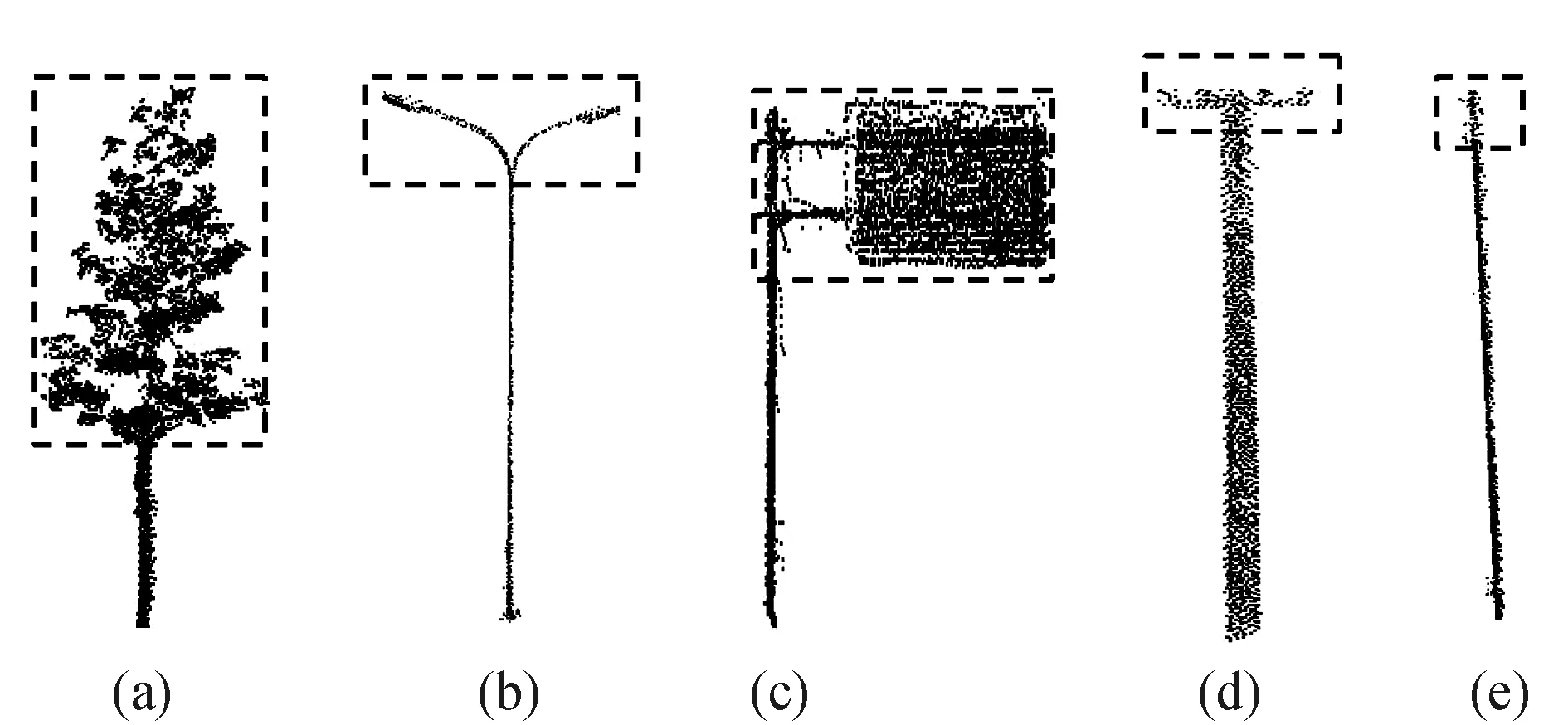
图1 5种典型杆状地物
1.2 特征矩阵提取
点云基本特征包括X,Y,Z空间信息、GPS时间信息、回波强度等,但单个点云的基本信息难以为分类提供有效支持。因此,本文通过计算点云组的特征向量、点云密度、顶部与杆部投影面积比值、拟合后总残差及拟合中误差构建特征矩阵。
不同杆状地物顶部形态不同,根据PCA(Principal Component Analysis)理论,对取出的杆状地物顶部点云数据构成的X,Y,Z矩阵进行奇异值分解,将原始坐标轴变换至杆状地物顶部点云主成分方向,并提取出顶部点云3个方向的特征值m1,m2,m3。由于不同种类地物3个方向特征值具有不同量纲,因此,对3个方向点云特征值进行数据归一化处理统一量纲,并将归一化后的特征向量a1,a2,a3,归入特征矩阵F。
(1)
不同杆状地物顶部点云在进行主成分变换后,空间3个主平面上的点云密度表现不同,因此,将杆状地物顶部分点云分别向3个主平面进行投影,建立宽度为0.2 m的格网,对投影点云进行格网投影,统计格网数计算投影面积,计算点云总数与3个投影面的比值,求得杆状地物在3个主平面的点云密度Dm1,Dm2,Dm3作为3个特征值,图2中,图2(a)为标示牌原始点云视图,图2(b)为经PCA坐标变换后的点云视图,图2(c)、(d)、(e)分别为顶部点云向3个主方向的投影。

图2 顶部点云坐标变化及投影示意图
不同杆状地物由于顶部大小与跨度均有差异,而杆部投影均为圆或半圆形,因此以顶部投影与杆部投影比值作为识别点云的特征。通过与计算点云密度相同的方法计算杆状地物顶部与杆部在XOY平面上的投影面积,计算顶部投影Sup与底部投影SDown的比值R,并将R作为特征值输入矩阵F。
不同杆状地物头部的拟合表面不同,因此,选择一个相同拟合表面计算出不同杆状地物对同一拟合表面的适应程度差异,为兼顾计算精度与算法运算速度,本文采用RANSAC平面拟合,具体步骤如下:
1)随机选择3个点构建初平面;
2)计算3个点所构造的平面方程Ax+By+Cz+D=0;
3)将单个杆状地物顶部点云带入平面拟合方程计算中误差;
4)统计所有满足中误差阈值的点作为内点(liner),统计内点个数;
5)调整平面方程系数,进行1~4步的迭代,直至找到最佳模型,使得内点个数最多完成迭代。
通过计算拟合后每个杆状地物与拟合平面的总残差以及均方根误差,即拟合后保留的内点到拟合平面的水平距离的平方δ和与均方根误差σ,其中n为拟合后保留的内点个数,将每个顶部点云拟合后的总残差δ与残差均方根误差σ带入特征矩阵,至此完成特征矩阵构建,即F=[a1,a2,a3,Dm1,Dm2,Dm3,R,δ,σ]。
(2)
2 SVM分类
2.1 SVM分类模型
SVM分类算法是一种基于统计的有导式机器学习算法,由Vladimir N和Alexey Ya于1963年提出,被认为是机器学习众多分类算法中分类效果与鲁棒性最好方法之一。SVM常用于两类样本的分类问题,对于线性可分型样本集,即通过一条直线(2维)或平面(3维)便可将两类数据分开,SVM将建立一个平面,将两类地物完全分割,并且保证平面距离样本集的几何边界最大,该平面即为超平面,对于线性不可分样本集,SVM通过核函数将样本集映射至高维空间,并在高维空间中构建超平面。
假设有样本集(xi,yi),i=1,2,3,…,l;y∈(-1,1),且样本集线性可分,则分界的超平面与支持向量距离为1/‖w‖,w={w1,w2…w3},求取划分两数据集的判决函数可表示为
yi(wi·xi+b)≥1,i=1,2,…,l.
(3)
实际应用中,线性不可分情况较多,为线性不可分样本构建超平面时,需引入惩罚因子C与非负松弛变量ζ,即允许变量在一定范围内违反超平面约束,约束尺度由惩罚因子C决定,因此,超平面优化问题可表示为
(4)
(5)
利用拉格朗日方程将式(5)进行对偶化,引入核函数K,将低维样本集映射至高维空间,并降低内积计算时的复杂度,结果可表示为
K(xi,xj)=φ(xi)·φ(xj),
(6)
i=1,2…,l.
(7)
根据式(7)可得判决函数:
f(x)=sgn(w*·φ(x)+b*)=
2.2 技术流程
依靠原始车载LiDAR点云数据无法建立SVM模型进行分类,需对获取的数据进行预处理、目标地物提取、特征获取以及样本训练后,才能建立分类模型。由于本文只涉及杆状地物分类,因此将使用提取后的杆状地物作为样本,并将相同样本统一存放,不涉及滤波及杆状地物提取工作,本研究工作流程(见图3)如下:
1)对提取后的点云样本进行顶部与杆部分离,为建立特征矩阵Feature提供基础;
2)对样本数据集进行特征提取,并将提取的特征值存入特征矩阵;
3)将不同杆状地物附加标签(行道树-1,路灯-2,广告-3,电线杆-4);
4)对数据进行归一化处理统一量纲,并对样本集进行交叉验证以确定最优惩罚系数C值与核函数参数g值;
5)创建SVM模型,选取测试集验证模型分类精度。

图3 技术流程
3 实验分析
3.1 实验区选取
本实验采用SSW车载LiDAR系统进行数据获取,点云扫描间隔0.02 m,数据集采用本研究团队已建立的数据集,其中包括路灯、行道树、广告牌、电线杆等杆状地物共计1 000个,并以此作为样本训练集。并提取北京市昌平区(试验区1)以及河南省焦作市(试验区2)两段道路数据中的400根杆状地物作为测试集(见图4),其中,行道树、路灯各150根,广告牌、电线杆各50根,试验区1为往返扫描,杆状地物点云数据较为完整,试验区2为单侧扫描,杆状地物点云部分缺失,扫描车靠道路右侧行驶,道路右侧的数据质量优于道路左侧,测试集概况如表1所示。

图4 试验区点云

表1 试验数据概况
3.2 参数寻优与精度对比
杆状地物分类算法在Maltab2012a环境下实现,采用库函数libSVM作为算法实现工具,并使用径向基函数(RBF)作为SVM分类核函数,采用9个特征值构成的特征矩阵F作为训练集特征方程,使用mapminmax函数,对特征值进行归一化处理,并对测试集采用5对折交叉验证得到最优C值19.108,与g值5.278,建立SVM支持向量机分类模型,对测试集进行分类判别,计算模型分类精度与时间消耗。
为验证文中所述算法的正确性,选取文献[14]中采用的反射强度结合杆状地物空间与形态特征的分类方法与本文方法进行分类精度对比,并与不同数目训练样本以及不同数量特征向量构建的SVM模型进行对比,用于验证训练样本时多特征向量与足够训练样本的必要性。
对400个已提取的杆状地物采用文献[14]中提到的分类方法进行分类,根据4类杆状地物特征分别设置阈值进行反射强度滤波、点云数量滤波、海拔滤波、高度滤波以及形态滤波对杆状地物点云进行分类。分类结果如表2所示,采用点云特征并通过先验知识人为设置阈值对测试集进行分类时,特征突出的杆状地物识别效果较好,部分杆状地物由于点云缺失或形态与其他同类别地物差异较大,采用阈值判断难以有效识别,因而导致错分与漏分,相比下,对SVM模型进行训练时,训练集样本中包含各类形态的杆状地物,对特殊形态的杆状地物具有良好的包容性,因此分类时表现较好,各类地物分类精度均较高,图(5)为测试集分类后结果,其中图5(a)、图5(b)分别为试验区一、试验区二使用SVM模型分类后效果,图5(c)为虚线框中SVM模型分类效果,图5(d)为虚线框中特征分类后效果,图中红色为识别的路灯点云,蓝色为行道树点云,绿色为广告牌点云,黑色为无法分类点云。

表2 两种方法分类精度对比
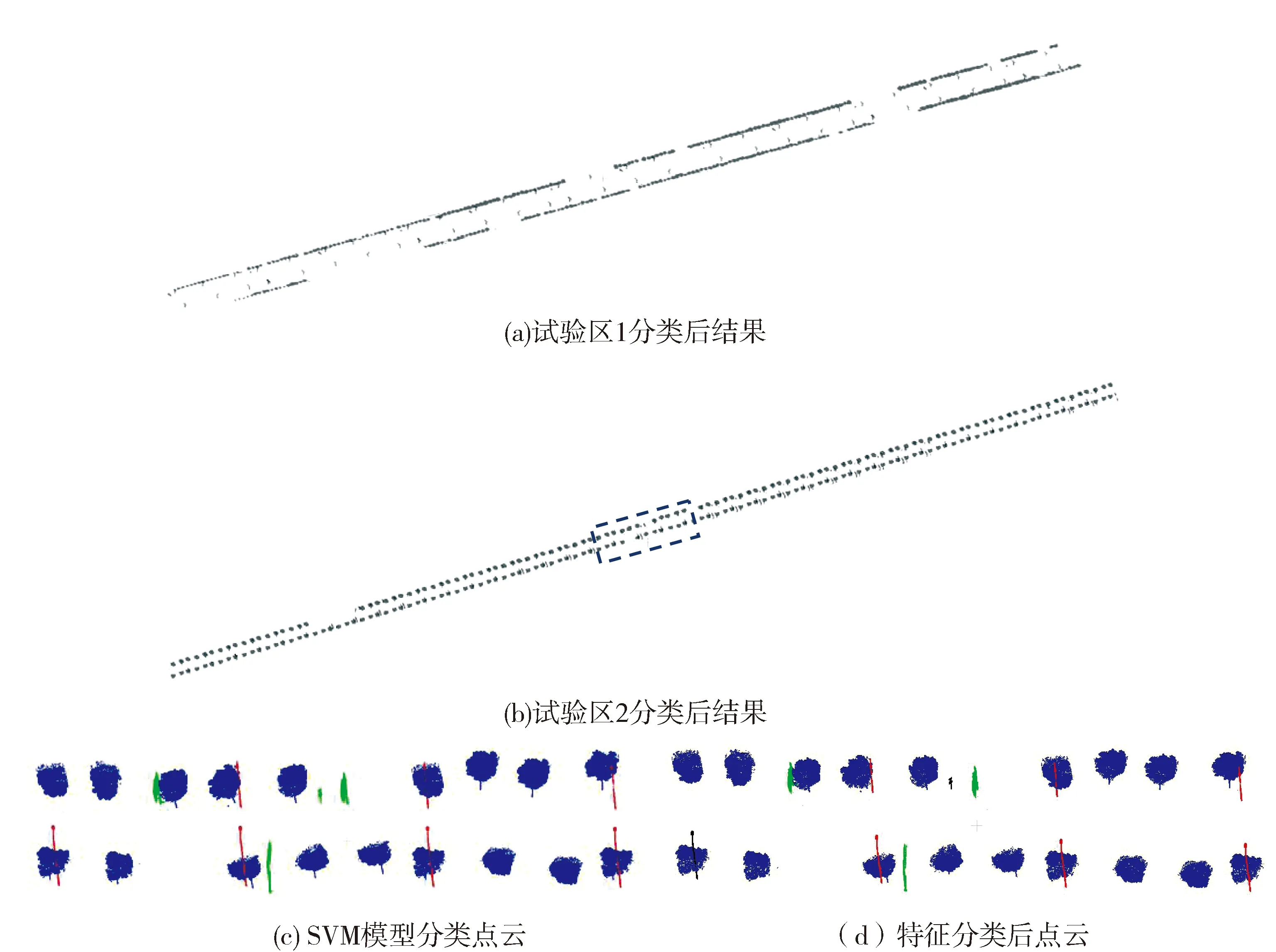
图5 分类后点云
采用不同数量的训练样本构建SVM模型,将训练样本集分为3类,样本数量分别为200,400和800。3种不同模型对同一测试集进行测试,实验结果与相关参数如表3所示,由实验结果可知,模型分类精度随训练样本数量增大而提高,究其原因,训练集数量较小时,数据所包含的数据类型较少,而杆状地物种类丰富,车载LiDAR工作时受扫描角度与周围环境限制,对不同杆状地物的扫描覆盖率也有不同,因此,少量数据集难以体现杆状地物全部特征,从而造成分类精度降低。

表3 不同样本数构造的3种模型分类精度对比
采用相同训练样本不同数量特征值进行对比试验,将训练样本分为3类,类别1特征矩阵构造为F=[Dm1,Dm2,Dm3,R,δ,σ];类别2特征矩阵构造为F=[a1,a2,a3,R,δ,σ];类别3特征矩阵构造为F=[a1,a2,a3,Dm1,Dm2,Dm3],训练样本数均为杆状地物1 000根,不同训练样本所消耗时间及分类精确度如表4所示,由实验结果可知,各组分类精度差别不大,减少特征矩阵中的特征数量,会降低SVM模型对测试集的分类精度,原因在于,部分杆状地物单个或多个特征相似,当选取特征不足时,难以构建优越的SVM模型对杆状地物进行种类识别,但识别率均高于几何特征分类杆状地物。

表4 不同特征矩阵构造的3种模型分类精度对比
4 结束语
本文以车载LiDAR点云作为原始数据,将杆状地物拆分为顶部与杆部两部分,对杆状地物点云进行9种特征获取并构建特征矩阵,以此为基础,采用SVM训练样本构建分类模型,实验证明,构建的SVM模型对杆状地物分类精度可达94.7%,精确度高于使用先验知识设置阈值的方法对杆状地物进行分类。基于SVM的杆状地物分类方法,有效避免了分类时的人为干预与阈值预设,适应性好、分类精度高,对提高点云自动化分类精度与效率具有较高的研究价值,但使用SVM模型进行杆状地物分类时,要求杆状地物具有较高孤立性,对于组合地物则无法正常提取特征与分类,因此对于组合地物的分割问题将成为今后研究的重点。

