基于Kriging模型的工业机器人定位精度补偿方法

柳 松，张德权，吴锦辉，张 宁，刘海涛

（河北工业大学 机械工程学院，天津 300401）

0 引言

随着工业自动化水平的提高，工业机器人逐渐成为自动化生产领域的核心装备[1]。定位精度是影响工业机器人性能的重要指标之一，包括重复定位精度和绝对定位精度。与重复定位精度相比，工业机器人的绝对定位精度更低，因此其更能反映机器人性能的好坏。影响工业机器人重复定位精度的因素有很多，如加工制造精度不足、工作环境温度、负载变化以及运动学参数误差等等。工业机器人在运行过程中的结构磨损、材料老化、齿轮齿隙变大等也会造成工业机器人的绝对定位精度会逐渐降低，从而影响产品的加工制造精度，而采用误差补偿方法提高工业机器人的绝对定位精度是一种行之有效的方法[2]。

在工业机器人末端的定位误差来源中，80%～90%是机器人运动学参数误差所引起的定位误差[3]。因此在对工业机器人进行误差补偿时，主要通过对运动学参数的补偿来提高机器人的绝对定位精度。针对工业机器人的精度补偿，已有不少学者开展了相关研究。王一等[4]以修正的D-H模型（即MD-H模型[5]）为基础，提出一种基于相对定位误差的工业机器人误差补偿模型，并考虑机器人负载和自重造成柔度误差的影响，对工业机器人进行误差补偿。周炜等[6]在传统机器人参数标定方法的基础上，提出一种基于空间插值的工业机器人精度补偿方法，并利用试验对方法的正确性进行了验证。该方法通过对工业机器人的工作空间进行网格划分，并根据定位误差相似度，实现对工业机器人的精度补偿，但当立方体网格太大时，该方法的补偿精度有所下降。洪鹏等[7]提出一种基于空间网格化的工业机器人变参数误差模型，并利用激光跟踪仪对KUKA机器人进行运动学标定，验证了方法的补偿效果。该方法考虑了工业机器人的定位误差在空间分布不均匀以及连杆柔度误差，但网格划分的数量极大地影响了该方法的补偿效果。齐飞等[8]基于工业机器人的位姿误差模型，通过冗余参数分析和最小二乘法修正了机器人的几何参数，并通过迭代补偿提高工业机器人的定位精度。该方法增加了机器人几何参数辨识的鲁棒性和准确性，但其在x坐标方向和y坐标方向的补偿精度较低。Wang等[9]利用神经网络的自学习能力和容错性好的特点，提出一种基于神经网络的工业机器人定位误差估计方法，并进行仿真验证。神经网络模型能够有效地提高工业机器人的定位精度，并具有实时性，但神经网路的训练需要大量的数据，在进行实际应用时增加了测量工作。Chen等[10]考虑到工业机器人的绝对定位误差与x，y，z轴上的定位误差具有空间相似性，提出一种基于co-Kriging的精度补偿方法，并以航空钻孔机器人为研究对象进行了实际补偿试验。Zeng等[11]提出一种基于误差相似度的机器人误差补偿方法，利用半方差函数对工业机器人定位误差进行量化，并结合激光跟踪仪进行了试验验证。该方法在一定程度上提高了工业机器人的绝对定位误差，但该方法的补偿效果受到半方差函数类型的影响。

针对上述问题，本文提出一种基于Kriging模型的工业机器人定位精度补偿方法。该方法根据工业机器人的名义位置及对应的定位误差，建立两者之间的Kriging模型，进而预测工业机器人在工作空间任意位置的定位误差。将预测的定位误差逆补偿至名义位置上，从而对工业机器人进行精度补偿，提高工业机器人的绝对定位精度。该方法可全面考虑各种影响工业机器人定位精度的因素，建模过程简单，补偿精度高，适用广泛。

1 工业机器人定位误差模型

1.1机器人运动学分析

D-H模型[12]常用来对工业机器人进行运动学分析。设ai表示连杆i的长度，di表示连杆i-1到连杆i的偏置距离，αi表示连杆i的扭角，θi表示关节i的转角，则连杆i-1到连杆i的齐次变换矩阵Ai可描述为

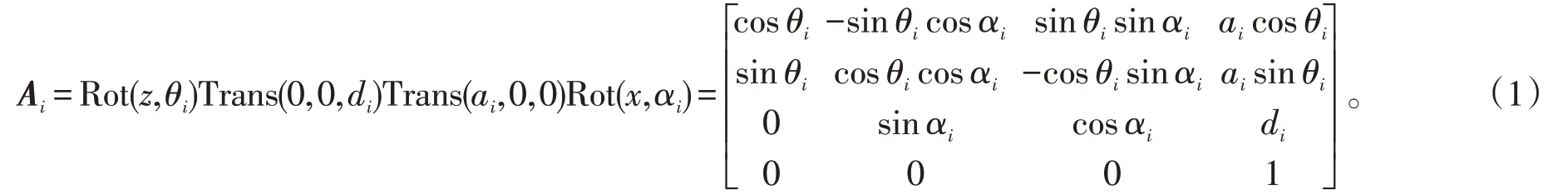
引入姿态矢量和位置矢量，式（1）可转变为

式中：ni，oi，ai为3个姿态矢量，表示连杆i的坐标系相对于连杆i-1坐标系的方向余弦；Pi为连杆i相对于连杆i-1的位置矢量。

对于n自由度的工业机器人，机器人末端坐标系相对于机器人基坐标系的变换矩阵为

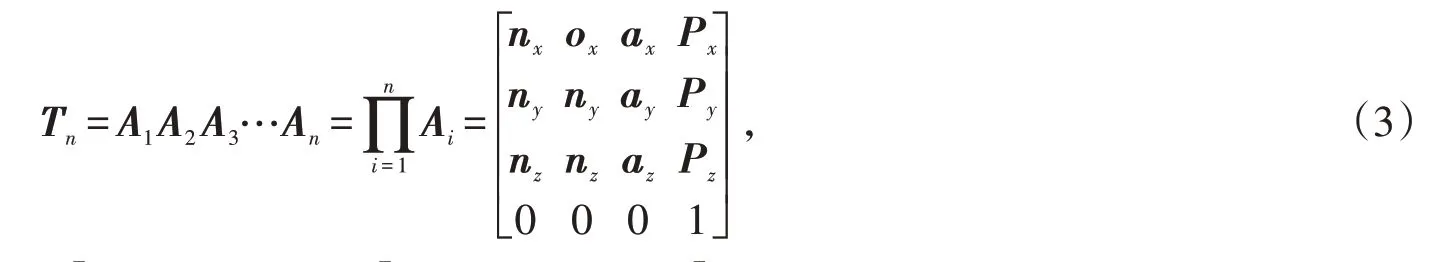
1.2 定位误差模型

由1.1节描述可知，齐次变换矩阵Ai依赖于它的4个参数ai、di、αi和θi。当工业机器人运动时，根据微分理论，对式（1）两边取微分，可得

由式（1）和式（4）可得，Qa，Qα，Qd和Qθ分别可表示为

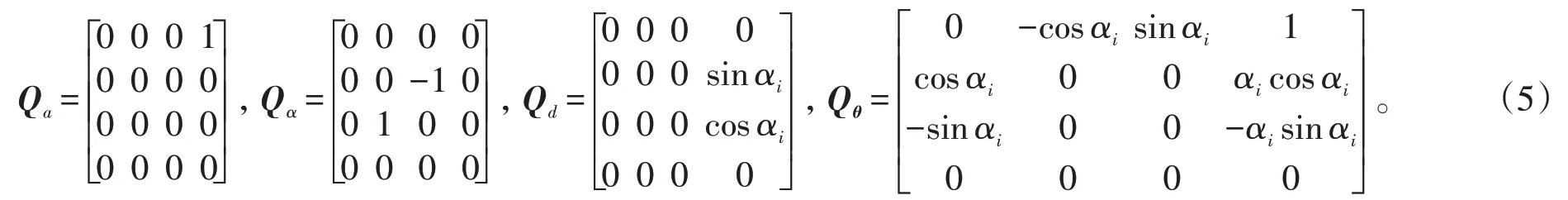
式（4）也可表示为dAi=Ai·δAi，δAi为Ai的误差矩阵，其表达式为

将式（5）代入式（6）可得

式中：cαi、sαi分别为cosαi、sinαi的缩写；δxiA、δyiA和δziA表示相对于i关节坐标系各坐标轴的旋转误差；dxiA、dyiA和dziA表示相对于i关节坐标系各坐标轴的位置误差。

根据式（7）可得，相对于i关节坐标系各坐标轴的位置误差矢量和旋转误差矢量分别为

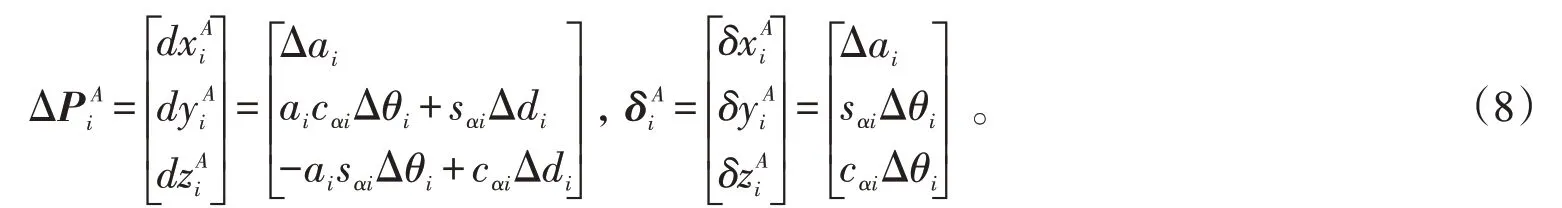
参照式（4），相对于i关节坐标系的位置误差可用位置矢量Pi的微分形式表达，即

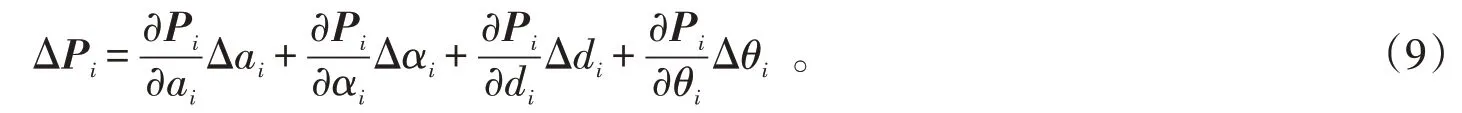
对于六轴工业机器人，Δθ、Δa、Δα和Δd均由6个元素组成的矢量，当工业机器人转动时，a、α和d中的元素均为常数，只有关节转角θ为变量。因此，机器人末端的位置误差ΔP可表示为关于θ的函数，即

2 基于Kriging模型的定位精度补偿

2.1 Kriging基本理论

Kriging模型是以变异函数理论为基础，并基于协方差函数对随机场进行建模和预测的回归算法[13]。其表达式为

式中：g(x)为实际函数值；f(x)为回归函数，表示模型的全局近似；β为回归系数；z(x)为服从正态分布N(0,σ2)的平稳高斯过程，表示对回归模型的偏差。z(x)的协方差为

式中，Rθ(xi,xj)为样本点xi与xj的相关函数，最常用的形式是高斯相关函数[14]，其表达式为

式中：n为设计样本空间的维数；m表示θ、xi和xj的第m个元素。

给定n维训练样本集x1,x2,…,xn及对应的实际响应值g，其中g=[g1,g2,…,gn]T，则对于待测点x，其Kriging预测值为

式中：β̂为β的广义最小二乘解，如式（15）所示；r(x)表示待测点x与其他训练点xi(i=1,2,…,n)之间的相关函数向量，可由式（16）表示。

考虑到Kriging模型可以给出空间最佳线性无偏估计[13]，本文采用Kriging模型建立工业机器人的名义位置与对应的定位误差之间的映射关系，从而预测工业机器人在工作空间任意点的定位误差。

2.2 基于Kriging模型的误差补偿

由于工业机器人零部件的加工制造误差，齿轮尺侧的间隙，机械臂与关节的柔性及结构部件的磨损等因素，造成工业机器人末端执行器实际位置与名义位置之间产生误差，从而使工业机器人产生定位误差。设机器人末端执行器在点P的定位误差为e(P)，其表达式为

式中：ex(P)，ey(P)和ez(P)分别为P点定位误差在x，y，z3个方向的误差分量；ed(P)为P点的绝对定位误差，其表达式为

由式（18）可知，P点的绝对定位误差ed(P)是关于ex(P)，ey(P)和ez(P)的函数，因此，确定P点各坐标方向的误差之后，P点的绝对定位误差即可求得。

根据已测得的工业机器人的名义位置Pt及对应的定位误差e(P)，并以名义位置Pt为输入，定位误差e(P)为输出，建立Kriging模型，则工业机器人在工作空间的任意位置的定位误差均可由已建立的Kriging模型进行预测。将工业机器人拟到达的名义位置输入Kriging模型中，即可得到定位误差的预测值ê(P)。根据得到的ê(P)对工业机器人进行误差补偿，补偿后机器人所要到达的名义位置如式（19）所示。补偿后的名义位置为工业机器人的实际到达点位，从而提高了工业机器人的绝对定位精度。

3 仿真验证

对该方法进行仿真验证时，主要考虑运动学参数误差对工业机器人定位精度的影响。以KUKA KR150-2型工业机器人为研究对象，如图1所示，采用基于Kriging的误差补偿方法对其进行定位精度补偿，从而验证本文所提方法的有效性。其D-H参数如表1所示。

采用KUKA KR150-2型工业机器人对本方法进验证时，采用以下步骤。

第1步，给定工业机器人运动学参数的几何误差值。参考文献[15]给定的工业机器人几何参数误差值，如表2所示，建立该型号工业机器人运动学误差模型。

第2步，在工业机器人工作空间中随机选定若干个定位点，记为工业机器人的名义位置Pt。应用表1中工业机器人的名义D-H参数进行运动学逆解，得到对应的名义关节转角θt。

图1 KUKA KR150-2型工业机器人结构示意图[2]Fig.1 The structural diagram of KUKA KR150-2

第3步，将名义关节转角θt输入含误差的D-H模型中，即表1和表2对应参数值相加，然后进行运动学正解，从而得到工业机器人实际到达点Pa。此时，工业机器人的定位误差为e(P)=Pa-Pt。

第4步，以工业机器人的名义位置Pt为输入，定位误差的各坐标方向分量ex(P)、ey(P)、ez(P)分别为输出，建立Kriging模型。

第5步，采用其他定位点对模型进行验证。将待测点的名义位置P′输入第4步建立的Kriging模型中，得到对应的定位误差补偿预测值ê(P′)，比较e(P′)与ê(P′)，从而判断基于Kriging模型的误差补偿方法的有效性。

为验证方法的正确性，对该方法进行举例说明。采用拉丁超立方抽样在工业机器人工作空间中随机抽取150个定位点，然后根据上述步骤采用任意50个点的名义位置和对应的定位误差建立Kriging模型，并以剩余100个点作为待测点，用来检验模型的正确性。结果如图2所示。对比图2a）～2c）可发现，对于含误差的D-H模型，工业机器人在y方向的定位误差预测值最大，最大值为1.879 3 mm，平均误差预测值为1.574 5 mm，z方向的平均误差预测值最小，仅为0.267 4 mm，预测结果如表3所示。由表3可知，该型号工业机器人在y方向的定位精度最差，而z方向的定位精度最好，波动范围最小，由Kriging模型预测的单点定位误差平均值为1.677 8 mm。Kriging模型预测的精度补偿值与实际精度补偿值的对比如图2中红线和黑线所示。从图2中可以看出，实际的精度补偿值和预测的精度补偿值基本相同，且对比结果在表4有所体现。由表4可知，采用Kriging模型的精度补偿方法所预测的精度补偿值与工业机器人的实际精度补偿值相比，单坐标方向和单点的对比误差均小于0.01 mm，最小值均为0 mm。图2中的蓝线为采用预测的补偿值对工业机器人末端位置进行补偿后的结果。经过精度补偿后，KUKA KR150-2型工业机器人的末端实际位置与名义位置基本重合，单坐标方向的最大误差仅为0.008 2 mm，单点最大补偿后误差为0.008 4 mm。经过仿真验证，基于Kriging模型的定位精度补偿方法在工程上是可行的，经过补偿后工业机器人的实际位置与名义位置基本重合，有效地提高了工业机器人的绝对定位精度水平。

表1 KUKA KR150-2型工业机器人D-H参数表Tab.1 D-H parameters of KUKA KR150-2

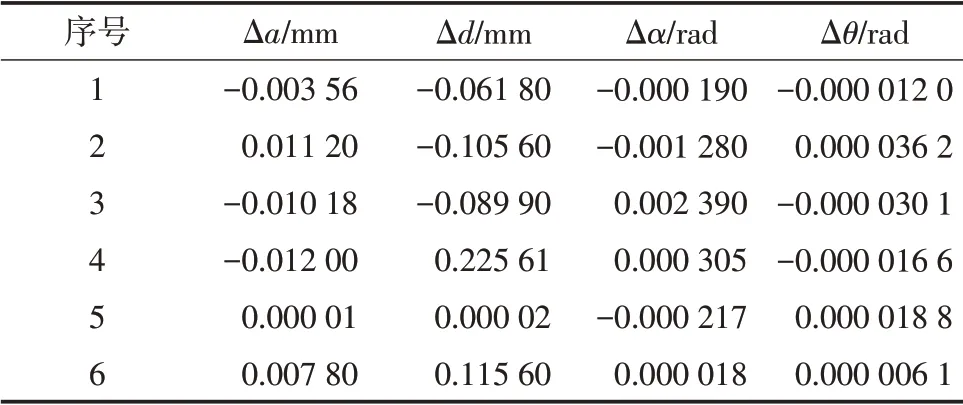
表2 KUKA KR150-2型工业机器人几何参数误差Tab.2 Geometric parameters error of KUKA KR150-2

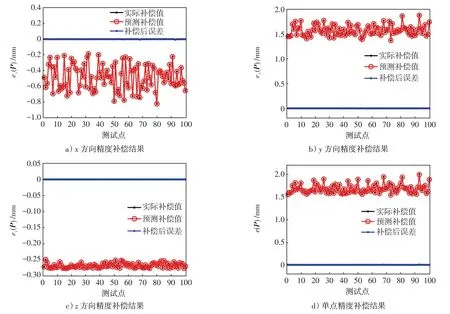
图2 定位精度补偿仿真结果Fig.2 Simulation results of positioning accuracy compensation

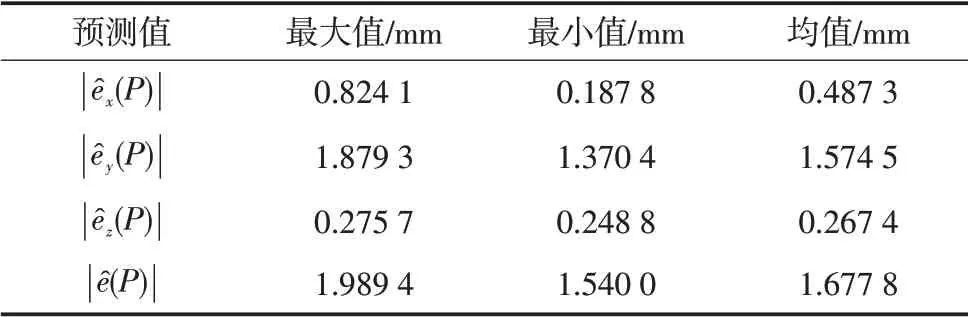
表3 模型预测精度补偿值Tab.3 The value of model predicted accuracy compensation

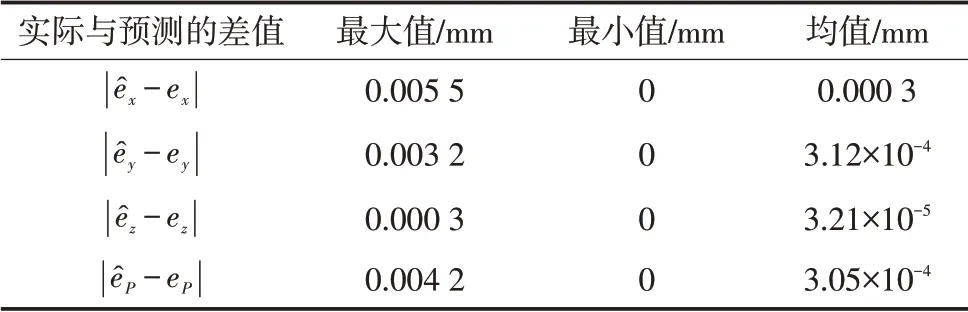
表4 预测补偿值与实际补偿值的对比Tab.4 Comparison of predicted compensation and actual compensation

4 结论

本文针对工业机器人绝对定位精度低的特点，提出一种基于Kriging模型的定位精度补偿方法。根据工业机器人所要到达的名义位置及对应的定位误差建立Kriging模型，从而对工业机器人的定位误差进行预测，进而根据预测的定位误差对工业机器人进行精度补偿。

1）与传统的精度补偿方法不同，本方法根据建立的Kriging模型预测任意位置的定位误差，将预测值逆补偿至名义位置上。根据补偿后的名义位置进行运动学逆解求得对应关节转角，使工业机器人进行运动，从而提高其绝对定位精度。

2）以KUKA KR150-2工业机器人为研究对象，对本方法进行了仿真验证。由结果可知，工业机器人在任意点的定位误差预测值与实际定位误差基本相同，最大偏差仅为0.005 5 mm。经过补偿后，工业机器人的绝对定位精度在单坐标方向的最大值为0.008 2 mm，单点绝对定位精度最大值为0.008 4 mm，平均值为0.001 8 mm。

3）仿真验证时主要考虑了运动学参数误差对定位精度的影响，在实际工作过程中，工业机器人定位精度还会受到其他因素影响，如负载变化、环境温度和零部件磨损等，在后续工作中会进一步研究。

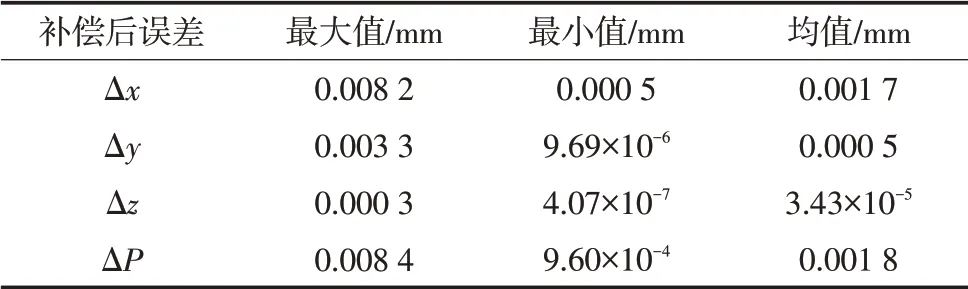
表5 补偿后机器人实际位置与名义位置的误差Tab.5 The error of actual position and nominal position after compensation