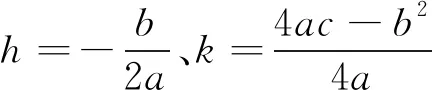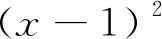初中数学二次函数问题的解题策略
王 谦
(江苏省南通市幸福中学,江苏南通,226000)
1 数值代入
数值代入是求解二次函数有关问题的重要思路.对于已知抛物线或某一二次函数经过确定的坐标点的问题,此时将坐标数值代入函数的解析式中,通过处理等量关系实现求解,这就是数值代入.常考题型包括求解函数解析式等,在解答题、选择题中均有可能出现,在解题时要注意关注已知的点的坐标,一般来说,当确定三个坐标点并代入解析式后即可列方程组解得对应的值,即为所求答案.
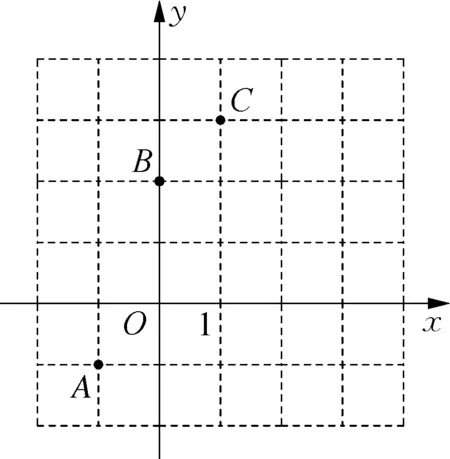
例1已知二次函数y=ax2+bx+c的图象经过A(-1,1),B(0,2),C(1,3),求二次函数的解析式.
思考:这类型问题就需要学生在做日常练习时清晰知道函数图象,本题直接将已知的横、纵坐标代入解析式,解二元一次方程组,根据得到的参数值得到二次函数的解析式.
解:由题意可得,A(-1,1),B(0,2),C(1,3),将上述三点代入y=ax2+bx+c.

因此,二次函数的解析式为y=-1x2+2x+2.
练习1无论m是任何实数,二次函数y=x2+(2-m)x+m的图象总经过的点是( ).
A. (-1,0) B. (1,0)
C. (-1,0) D. (1,3)
思考:本题要快速解得正确的解,只需要分别将四个选项的坐标代入解析式中,通过等号两端是否相等判断正确答案,虽有参数m,但可以利用代入的数将其消除,代入等式求解.
解:将横坐标代入x,纵坐标代入y.




评析:学习函数与类似的坐标数值紧密相关,是解答二次函数相关问题必需的基本技能之一,关键是因为函数解析式是函数与相应自变量之间的一种数量关系.
2 图象说理
二次函数具有一定的抽象性,利用图象解答相关问题就有重要作用,看懂抛物线等特殊图象表达的特殊意义,例如其中反应的函数范围和自变量的变化,数量关系是怎样的,是利用图象解题的重要手段.常见的考查题型包括求解自变量的取值范围,比较两个函数值的大小等,主要以选择题的形式出现,在解答题中也有一定涉及.
例2二次函数y=x2-2x-3的图象如图所示,当y<0时,自变量x的取值范围是( ).
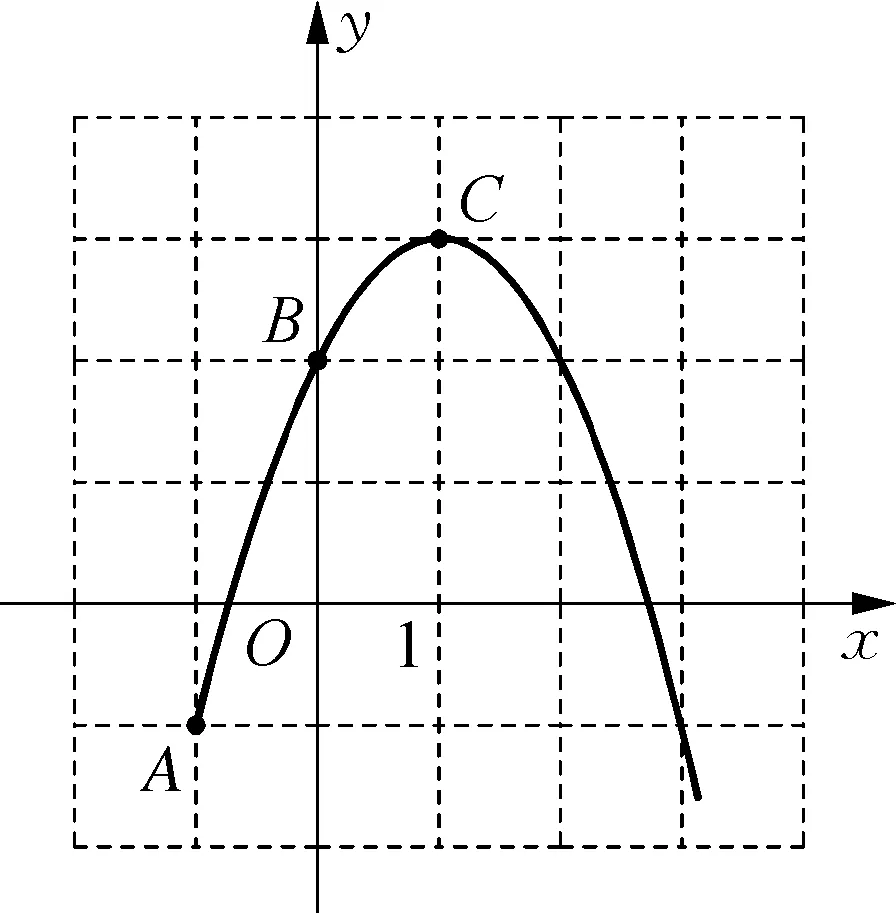
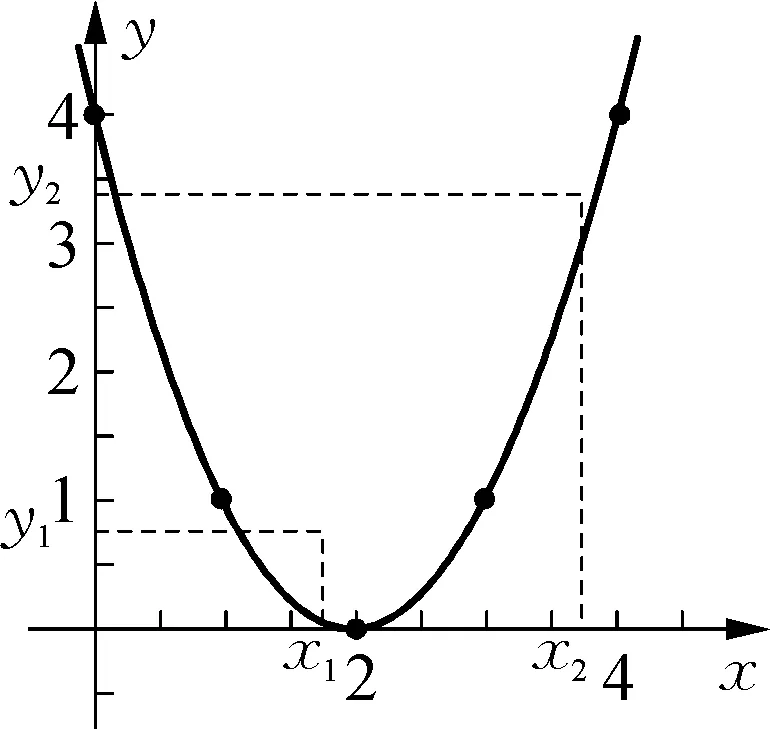
A.-1 C.x>3 D.x<-1或x>3 思考:本题首先需要明白抛物线的哪一段代表y<0,并观察图象得到此时自变量的取值范围,即为所求的解. 解:如图所示,为函数y=x2-2x-3的图象. 由题意可得,当y<0时,为x轴下方的一段. ∴这段抛物线对应的取值范围是在-1到3之间. 故自变量x的取值范围为-1 练习2已知二次函数y=ax2+bx+c(a≠0)中,其函数y与自变量x之间的部分对应值如下表所示: x…01234…y…41014… 点A(x1、y2)、B(x2、y2)在函数的图象上,则当1 A.y1>y2B.y1 C.y1≥y2D.y1≤y2 思考:本题根据已知的二次函数y与x的对应关系得到函数图象,然后分析抛物线的对称轴方程求出其对称轴,利用二次函数的增减性即可判断出y1、y2的大小关系. 解:根据题意已知y=ax2+bx+c(a≠0). ∵当x=0时,y=4;x=1时,y=1;x=2时,y=0代入函数解析式. ∴此抛物线的解析式为:y=x2-4x+4. 如图所示,该抛物线的开口向上. ∴抛物线的顶点为(2、0). ∵-1 ∴y1 评析:根据上述两个例题可以发现,要具有良好的观察能力才能正确分析图象问题,最大限度发挥“图象说理”的作用,快速求解. 将图象用坐标系表示是函数的特点之一,二次函数具有解析式与图象一一对应的关系,因此利用两者之间“数”与“形”之间的密切联系是解题的新思路.如下表所示是不同形式解析式的图象开口方向、对称轴和顶点坐标等值,需要同学们理解记忆,还可以转化为如下所示的图象转换关系,解题时要利用其内在联系,掌握关键.在选择题、填空题或解答题中均会运用到数形结合,这是同学们一定要掌握的内容. 函数解析式备注开口方向对称轴顶点坐标y=ax2(a≠0)特例y=ax2+k(a≠0)特例y=a(x-h)2(a≠0)特例y=a(x-h)2+k(a≠0)顶点形式y=ax2+bx+c(a≠0)一般形式a>0,开口向上a<0,开口向下直线x=0(y轴)(0,0)直线x=0(y轴)(0,k)直线x=h(h,0)直线x=h(h,k)直线x=-b2a-b2a,4ac-b24a 例3将抛物线y=5x2先向右平移3个单位,再向上平移2的单位后,所得的抛物线的解析式为( ). C.y=5(x-3)2+2 D.y=5(x-3)2-2 思路:本题考查了二次函数图象与几何变换,利用顶点的变化确定函数解析式求解更简单,可以根据向右平移横坐标加,向上平移纵坐标加得到平移后的抛物线的顶点坐标,然后利用顶点式得到解析式即可. 解:∵y=5x2先向右平移3个单位,再向上平移2的单位得到顶点坐标为(3,2). ∴所得的抛物线的解析式为y=5(x-3)2+2. 故正确答案为C选项. 练习3与抛物线y=-5x2-1顶点相同,形状也相同,而开口方向相反的抛物线所对应的函数是( ). A.y=-5x2-1 B.y=5x2-1 C.y=-5x2+1 D.y=5x2+1 思考:本题考查了二次函数的性质,二次函数的解析式中,二次项系数确定函数的开口方向,熟练掌握二次函数的性质是解题的关键.顶点相同,形状也相同,而开口方向相反的抛物线,即与原式只有二次项系数不同. 解:与抛物线y=-5x2-1顶点相同,形象也相同,而开口方向相反的抛物线. 即与抛物线y=-5x2-1只有二次项系数不同. ∴y=5x2-1,正确答案为B选项. 例4抛物线y=ax2+bx+c经过点A(-1,0),B(3,0),则此抛物线的对称轴是直线x=. 思考:本题考查了二次函数的对称性,抛物线经过两个点的纵坐标均等于零,借此确定对称轴. 解:由题意可得,抛物线经过了点A(-1,0),B(3,0). ∵纵坐标相等. ∴它们是抛物线上的对称点. ∴它们的对称轴时两点横坐标的平均数. ∴A、B两点是抛物线上的两个对称点. 故正确答案为2. 练习4已知二次函数y=ax2+bx+2的图象经过点A(-1,1),B(0,2),C(1,3),(1) 求二次函数的解析式;(2) 画出二次函数的图象. 思考:本题可以利用顶点形式的“数”来了解“形”,可以通过顶点公式和对称轴公式解得对应的值,然后画出图象实现求解. 解:(1)y=-x2+2x+2,过程略; (2) 将y=ax2+bx+2(a≠0)形式配方成:y=a(x-h)2+k(a≠0)形式. ∵y=-x2+2x+2. ∴对称轴为x=1,顶点为(1,3),a=-1<0. ∴图象经过点(3,-1)和(2,2),且该图象是对称的. 故分别与点A(-1,1),B(0,2)关于对称轴对称得到图象,如图所示: 评析:上述两个问题均是比较简单的数形结合问题,解题时要根据题意灵活处理图形变换,要熟悉图形相关的知识点,最后实现求解. 对于初中数学二次函数问题的相关解题策略还有方程释义等手段,本文只着重介绍了以上三种,从上述三种策略可知,必须要熟练掌握不同形式的二次函数的变换形式,这是解题的重要内容.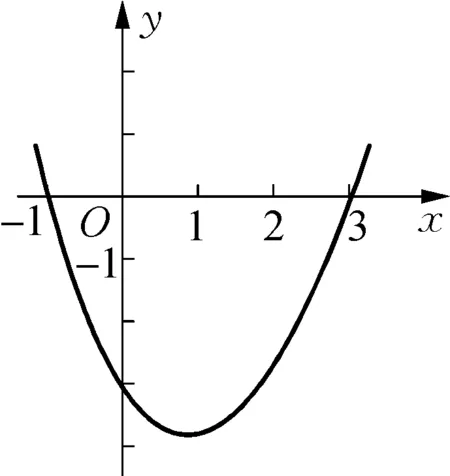


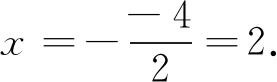
3 数形结合