抽象函数的几类常见问题及其解法
李佳坤
(云南省曲靖一中沾益清源学校,云南曲靖,655000)
什么是抽象函数呢?抽象函数就是指没有具体的函数解析式但知道某些性质的函数,但因为其具有强烈的抽象性、复杂性导致很多学生在遇到这类型的问题时思路混乱,对与其性质有关的问题更是无从下手,为了帮助同学们弄懂抽象函数的相关问题,本文对此作些探讨.
1 抽象函数的定义域问题
抽象函数的定义域问题,等价于复合函数定义域问题,可以细分为三种类型,但其主要形式为利用已知函数f(x)的定义域,求解函数f[g(x)]的定义域或者已知f[g(x)]的定义域求f(x)的定义域.求解抽象函数定义域的主要思路为:① 根据实际问题分析函数f(x)或f[g(x)]的定义域;② 利用复合函数的定义域进行求解,例如f(x)的定义域等于g(x)的值域,解出g(x)中自变量的取值范围,即等价所求的定义域.
例1当函数f(x)的定义域等于[1,2],试确定函数f(x+1)的定义域.
剖析本题已知原函数的定义域,则直接可得函数f(x+1)为[1,2]进而解得f(x+1)的定义域为[0,1].
解析因为f(x)的定义域等于[1,2],
所以:1≤x+1≤2,
解之得:0≤x≤1,
因此,函数f(x+1)的定义域等于[0,1].

剖析本题已知函数y=f(x)的定义域,则根据f(x)中x与f(log2x)中log2x的意义相同即可得到log2x的取值范围,进而解得函数f(log2x)的定义域.
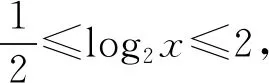
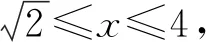
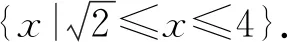
2 抽象函数的值域问题
抽象函数的值域问题,利用函数的定义域和对应法则的关系求解,对应法则和函数的定义域相同,则该函数的值域也一定相互对应(因为自变量的变化只影响函数图象的横向取值范围,并不影响纵向取值范围).求解抽象函数值域的主要思路为:① 根据实际问题分析原函数的值域;② 分析原函数与所求函数之间的定义域对应法则是否一致,相对应时,原函数的值域即等于所求函数的值域.
例2若函数y=f(x+1)的值域为[-1,1],则函数y=f(3x+2)的值域为.
剖析根据函数y=f(3x+2)和y=f(x+1)中的定义域对应法则完全相同,就可以直接得到函数y=f(3x+2)的值域.
解析由题意可得:y=f(x+1)的值域为[-1,1],
∴y=f(3x+2)的值域也为[-1,1].
拓展训练2:若函数y=f(x+2)的值域是[-2,2],则函数y=f(5x+3)的值域为.
剖析本题根据题意已知原函数值域为[-2,2],且函数y=f(x)与y=f(5x+3)的对应法则相同,故函数y=f(5x+3)的值域不变.
解析由题意可得函数y=f(x+2)的值域是[-2,2],
将y=f(x+2)向右平移两个单位,即得y=f(x)的图象,值域是[-2,2],
要得到函数y=f(5x+3),需要先将函数y=f(x)扩大到原来的5倍,
即y=f(5x),
再将y=f(5x)的图象向左平移三个单位,
即得y=f(5x+3)的图象,
∵函数y=f(5x+3)与函数y=f(x+2)的定义域对应法则相等,
因此,函数y=f(5x+3)的值域也是[-2,2].
3 抽象函数的周期性问题
例3f(x)是一个R上的奇函数,且恒有f(x-4)=-f(x)成立,已知该函数在区间[0,2]内是单调递增,如果在固定区间[-8,8]内方程f(x)=m(m>0)上有四个不等根x1、x2、x3、x4,那么x1+x2+x3+x4=.
剖析本题的关键在于利用周期和对称轴表示出x1、x2、x3、x4任意两数之间的和,函数f(x)的周期为8且对称轴为x=2,且在区间[0,2]单调递增,如图1所示,则有x1+x2=-12,x3+x4=4,继而求解.
解析由题意得,f(x)是奇函数,且恒有f(x-4)=-f(x),
∴f(x-4)=f(-x),
∴函数f(x)关于直线x=2对称,且f(0)=0,
又∵f(x-4)=-f(x)可知:f(x-8)=f(x),
∴函数f(x)的周期为8,
∵函数f(x)在区间[0,2]中单调递增,
∴f(x)在区间[-2,0]上也单调递增,
如图1所示,
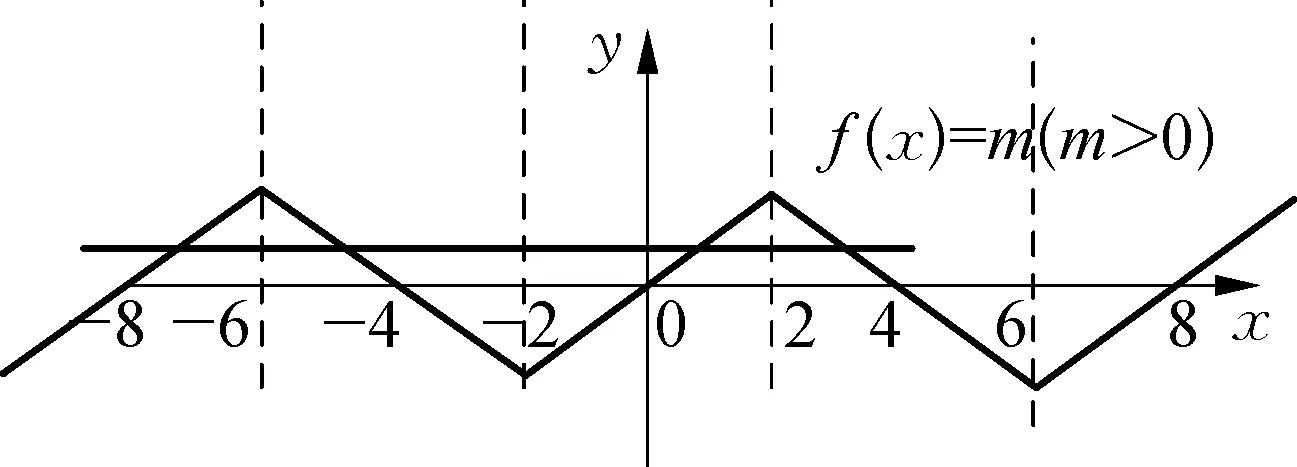
图1
∴当方程f(x)=m(m>0)上有四个不等根x1、x2、x3、x4时,令x1 根据函数的对称性可得:x1+x2=-12,x3+x4=4, 综上所述,x1+x2+x3+x4=-8. 剖析首先解题时要对所给条件进行分析,将问题中所给的偶函数性质以及对称性质用具体解析式表示,则有f(x)=f(2-x)和f(x)=f(-x),此时可得到f(2-x)=f(x)=f(-x).通过替换变量的方式,将其关系等式转化为f(x+T)=f(x)的形式,即可求出问题的周期性,也能证明f(x)是周期函数. 解析∵y=f(x)的图象关于直线x=1对称, ∴f(x)=f(2-x), 又∵f(x)是一个偶函数,即f(x)=f(-x), 则有f(-x)=f(2-x),x∈R, 用x替换上式中的-x替换即得:f(x)=(x+2), 综上可知,f(x)是周期函数,且周期等于2. 抽象函数的奇偶性相关问题在考题中也经常出现,通常以选择题形式进行命题.求解抽象函数奇偶性,应牢牢把握奇偶函数的定义,从而进行解题.解题的思路具体为:① 对问题所给的关系等式进行分析,将变量替换为相反数,得到与问题所求函数对应的具体解析式;② 若f(-x)=-f(x),函数则为奇函数;若f(-x)=f(x),函数则为偶函数,判断所求函数的奇偶性质;③ 根据所求函数对应的具体奇偶性,求出问题所求的值的大小. 例4已知f(x)、g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( ). A.-3 B.-1 C.1 D.3 剖析本题主要考查函数奇偶性的理解和运用,根据函数奇偶性的特点对原f(x)、g(x)变形,得到与其等价的函数,结合已知条件代入x=1即可正确求解. 解析由题意可得:f(x)=f(-x),g(x)=-g(-x), ∴f(1)+g(1)=f(-1)-g(-1), ∵f(-1)-g(-1)=(-1)3+(-1)2+1=1, ∴f(1)+g(1)=1. 拓展训练4:已知函数g(x)、f(x)都是奇函数,F(x)=af(x)+bg(x)+4(a、b∈R),且F(-1)=5,则F(1)=. A. -5 B.-1 C.3 D.4 剖析由于问题对函数具体值进行求解,则应求出F(x)=af(x)+bg(x)+4的奇偶性质.解析式中包含有常数4使求解复杂化,故将af(x)+bg(x)提取构造函数h(x),判断h(-x)与h(x)的关系,得到对应奇偶性质.结合F(-1)=5即可得到h(-1)的值,根据奇偶性质得到h(1)的大小,即可求出F(1)=h(1)+4的具体值的大小. 解析设h(x)=af(x)+bg(x), ∵h(-x)=af(-x)+bg(-x)=-(af(x)+bg(x))=-h(x), ∴函数h(x)为奇函数, 又∵F(-1)=5, ∴F(-1)=h(-1)+4=5, 可得h(-1)=1, 故F(1)=h(1)+4=-1+4=3. 抽象函数对称性问题的解答,主要围绕对称性对应的关系等式展开求解,例如函数f(x)关于(a,b)对称则有等式f(x)+f(2a-x)=2b,运用该关系等式能求解抽象函数的对称性问题.具体的解题思路为:① 对问题所给条件进行分析,结合具体的对称关系等式,判断所求函数f(x)的具体对称直线或对称点;② 利用推导已知的对称直线或对称点,求出问题所求的具体值的大小,对问题做出解答. 例5若函数y=f(x)的反函数为y=f-1(x),则函数y=f(x-1)与函数y=f-1(x-1)的图象为( ) A.关于直线y=x对称 B.关于直线y=x-1对称 C.关于直线y=x+1对称 D.关于直线y=1对称. 剖析本题需要根据已知函数的函数y=f(x)与其反函数为y=f-1(x)的图象推断,根据左加右减原则,得到函数y=f(x-1)与其反函数的对称轴. 解析由题意可得:原函数y=f(x)和反函数y=f-1(x)的图象关于直线y=x对称, ∵函数y=f(x-1)与函数y=f-1(x-1)等价于将原函数y=f(x)及其反函数为y=f-1(x)的图象同时向右平移一个单位, ∴它们的对称轴也对应向右平移一个单位, ∴函数y=f(x-1)与函数y=f-1(x-1)的对称轴为y=x-1, 故正确选项为B选项. 拓展训练5:已知函数y=f(x)对任意的x都满足f(3+x)=f(3-x),且方程f(x)=0时有六个不同的解,试确定这六个解相加的值. 剖析对问题已知条件进行分析,可发现关系等式f(3+x)=f(3-x)可推导出函数f(x)关于直线x=3对称,此时可利用该对称轴进行解题.由于f(x)=0有6个不同解,可推断这6个解分别关于x=3对称,此时可得到对应的关系等式,根据关系等式求出问题所求的最后值即可. 解析∵f(3+x)=f(3-x)对任意x均成立, ∴函数图象关于直线x=3对称; 又∵f(x)=0时的6个实数根一定关于直线x=3成两两对称, ∴x1+x6=6、x2+x5=6、x3+x4=6, 则x1+x6+x2+x5+x3+x4=18. 关于抽象函数的问题,求解其周期性、定义域和值域是最基本的问题,除此之外,求解抽象函数的单调性问题、抽象函数的奇偶性问题等等也是常考的问题,因为抽象函数没有具体的函数式的特点,所以考查其基本性质的题目难度会比其他函数更复杂一点.抽象函数的性质都有对应的关系等式,对这些等式的熟悉也是解题要求的一部分.与抽象函数有关的考题中,最常考的知识就是抽象函数的性质,因为抽象函数没有具体的函数表达式,所以其抽象性比其他函数更强,对学生的逻辑思维能力要求更高,更能考查学生的思维严密性.因此同学们应更加需要重视关于抽象函数的性质问题求解思路的学习与形成.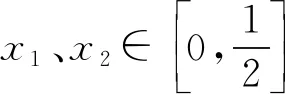
4 奇偶性问题
5 对称性问题

