基于频率无反演识别结构损伤的研究
曾宁烨
(中铁二院工程集团有限责任公司,四川成都 610031)
由于结构局部参数(如质量、刚度)的改变导致结构的局部损伤,进而引起结构模态参数(如频率、阻尼、振型)的改变,最后体现在结构动力学响应的改变上[1-3]。结构损伤识别就是通过实际测量反映结构力学特性的数据,对桥梁结构是否有损伤、损伤位置、损伤程度等作出准确合理的判断。
鉴于频率是目前测试技术所能达到的最准确也是最易测的模态参数[4],几乎可在结构的任何一点进行测量,国内外在利用频率进行结构损伤识别方面也作了大量研究[5]。这些研究方法按有无反演可分为2类:
(1)有反演的损伤识别方法(反面方法),是将待识别的未知量(结构参数、刚度矩阵、损伤指标等)看成优化变量,并组成目标函数,通过不断地修正有限元模型,得到结构的优化参数,使正向计算结果能够最大限度地与实测结果吻合,如Stubbs等[6]提出的整体损伤估计法,建立了频率变化量、广义刚度对单元刚度参数的灵敏度矩阵和损伤定位参数之间的线性方程组,由于所得的方程组高度欠定,迭代过程需要反复计算灵敏度矩阵,计算量很大,而且迭代没有终止的可靠判据,很难得出准确的结果。
杜思义等[7]在结构有限元计算模型中定义了单元的损伤识别参数,基于摄动理论和振动理论,推导了结构振动特征值的一阶和二阶摄动方程,建立了结构的一阶和二阶损伤识别方程,给出了两方程欠定条件下损伤识别参数的优化求解算法。在这种方法中,结构的损伤位置、损伤程度和老化程度的结构只需通过在役结构的固有频率的测量值就可以识别,这样就避免了使用模态振型识别结构损伤因测量精度不高或自由度不足带来的误差。
(2)无反演的损伤识别方法(正面方法),如固有频率向量法,特征值曲线交点法等。王乐等[8]引入固有频率向量及固有频率向量置信准则的概念,形成固有频率向量损伤特征数据库,从而提出基于固有频率向量的结构损伤检测方法。该方法可以在较强的测量噪音的干扰下,准确地识别出结构损伤的位置并能较准确的测出其损伤程度。特征值曲线交点法其原理最早是基于Cawley和Adams[9]提出的利用“频率变化比(频变比)”检测结构损伤的原理和方法。Hearn等[10]在此基础上又提出了“频率平方变化比”方法,指出当结构只有一个单元发生损伤时,任意两阶频率平方变化比只是损伤位置的函数,和损伤的程度大小没有关系。故以各单元发生不同损伤程度时“频率平方变化比”Δλi/Δλ1的平均值作为纵坐标,以单元编号为横坐标,作出Δλi/Δλ1对应的曲线图。根据实际工况损伤对应的“频率平方变化比”Δλi/Δλ1的值,在上述曲线图中作一条直线,直线与曲线的交点即为可能的损伤单元,此交点法即为“特征值曲线交点法”。
鉴于反面识别方法需要利用优化算法求解欠定方程组,其识别是个相当复杂的过程,本文仅从正面进行结构损伤诊断,阐述固有频率向量法与特征值曲线交点法的基本原理,以一简支梁数值模拟为例,比较2种方法的优缺点,并指出了有待进一步研究的问题。
1 结构损伤识别算法
1.1 固有频率向量法
1.1.1 固有频率向量及其组成的损伤特征数据库
采用有限元法将具有一定健康状态(完好或损伤)的结构离散后,会具有N个自由度,再用振动特征方程求解出其N阶固有频率,记为f1,f2,f3…fN,定义向量[F]={f1,f2,f3…fN}T为结构在该状态下的固有频率向量。显然,完整或损坏结构其各自的固有频率向量是唯一的和固有的。
假定完好结构状态及不同损伤位置、不同损伤程度对应的结构状态—记为Di,j(i表示损伤位置,j表示损伤程度),各自对应的固有频率向量{F}、{FDij}可以组成一个广义向量库,即为该结构的损伤特征数据库。通常{F}、{FDij}是在基准模型(通常是经过实测模态数据修正的有限元模型)的基础上计算出来的,通过数值模拟求解各状态对应的固有频率向量,从而建立损伤特征数据库。结构损伤特征库中进行基于固有频率向量的结构损伤检测。
1.1.2 固有频率向量置信准则
根据模态置信准则定义固有频率向量置信准则(natural frequencies vector assurance criterion,NFVAC)公式见式(1)。
(1)

1.1.3 损伤判据
从理论上讲,如果结构的固有频率向量在未知的损伤状态下与损伤特征数据库中某个向量所对应的结构损伤状态相同或非常接近,那么两向量的INFVAC值应等于1或非常接近1。然而,在数值模拟中,用穷举法计算结构在所有可能损伤状态下的固有频率向量是不可能的。因此,用这种方法进行识别时,得到的INFVAC值不可能精确等于1。故用IDNFVAC=1/(1-INFVAC)先对损伤指标进行转换,由公式(1)知,INFVAC∈ [0,1],显然IDNFVAC在[0,1]上单调递增,且IDNFVAC越接近于1,其值越大。
但由INFVAC的数学意义可知,其本质是求2个向量的相关性,只要2个向量互成比例,其相关性就等于1,但此时2个向量的模的偏差却可能很大,即相关性只能表征2个向量的方向或者比例;因而在考察向量的一致性时,不但要考虑向量的方向,同时也要考虑向量模的变化,显然,如果只考虑向量的相关性有可能造成损伤的误检。

损伤判据[11]定义为IDNFVAC值与平均偏差值ERR之比,显然同时考虑2个固有频率向量的相关性及这2个向量间的平均偏差,来衡量2个向量之间的一致性,公式见式(2)。
IDR=IDNFVAC/ERR
(2)
由于损伤数据库中的数据信息较大,在进行向量计算时,利用MATLAB编程实现。具体步骤为:
(1)计算完好结构及每个单元损伤不同程度后的频率形成损伤特征数据库。
(2)数值模拟指定工况的损伤,得一组频率列向量。
(3)利用式(1),将各工况所得的频率列向量与损伤特征库中的各个列向量相乘,将INFVAC值较大的对应的所有模式记为{Echange}。
(4)在{Echange}中,利用式(2)求IDR。
(5)结论:在{Echange}中IDR越大,则待检测结构的损伤模式就是对应的特征库中损伤模式。
1.2 特征值曲线交点法
具有N自由度的自由振动系统,其振动方程为式(3)。

(3)
若忽略阻尼的影响,其特征值由式(3)的特征方程求解得到式(4)。
([K]-λ[M])[φ]={0}
(4)
式中:[K]、[M]、λ、[φ]分别为结构的刚度矩阵、质量矩阵、特征值、特征向量(振型向量),其中λ=ω2,ω为结构的固有频率。
当结构遭到破坏时,结构的刚度和质量等会发生变化,从而导致结构的频率发生变化。因此,损伤识别可以根据自然结构振动频率的变化进行。设结构的刚度和质量矩阵[K]、[M]发生轻微变化[ΔK]、[ΔM],则结构的特征值λ和特征向量[φ]也会有微小的变化,另此变化为Δλ、[Δφ],则式(4)可以写作式(5)。
(([K]+[ΔK])-(λ+Δλ)([M]+
[ΔM]))([φ]+[Δφ])={0}
(5)
对于桥梁工程问题,结构损伤往往会影响构件和结构的刚度,但是对其质量没有明显的影响,因此可以忽略[ΔM]的影响,所以式(5)可以转换为式(6)。
(([K]+[ΔK])-(λ+Δλ)[M])([φ]+[Δφ])={0}
(6)
将式(6)化简,忽略二次项,可得式(7)。
(7)
对于其中某一个振型[φi] (i=1,2,……,N)来说,给出式(8)。
(8)
以[ΔKn]表示第n个单元刚度的变化,那么式(8)变为式(9)。
(9)
式(9)建立了结构刚度变化与结构特征值之间的关系。当仅第n个单元损伤时(即单个单元损伤时)为式(10)。
(10)
将结构特征值的变化定义为结构损伤位置与单元损伤程度的函数,有式(11)。
Δλ=Δλ(αn,n)
(11)
式中:αn为一标量,表示n单元的损伤程度,又[ΔKn]=αn[Kn],式(11)变为式(12)。
(12)
式(12)表示特征值的变化不仅依赖于结构损伤的位置,而且还依赖于结构损伤的程度。取两阶振型对应的特征值为Δλi及Δλj,两阶模态对应的频率变化比为式(13)。
(13)
式(13)表明:当结构只有一个单元发生损伤时,任意两阶频率平方变化比只是损伤位置的函数,和损伤的程度大小没有关系。
不同位置单元的损伤对应一组特定的“频率平方变化比”集合,根据结构损伤前后各阶模态对应的“频率平方变化比”,就可以识别结构的损伤位置。
基于以上理论,总结出用特征值曲线交点法进行结构损伤识别的步骤:
(1)计算出结构各单元损伤时对应的特征值,构建“频率平方变化比”指标,以作为损伤检测的理论值。根据式(13),以各单元不同损伤程度对应的“频率平方变化比”Δλi/Δλ1的平均值作为纵坐标,以单元编号为横坐标,作出Δλi/Δλ1(i=2,3)对应的曲线图。由于不同单元对应的“频率平方变化比”差异较大,这里采用对数坐标来表示。
(2)数值模拟指定工况的损伤,求出对应的“频率平方变化比”Δλi/Δλ1(i=2,3),并在步骤(1)的曲线图中作一条直线,直线与曲线的交点即为可能的损伤单元。
2 仿真算例
选择简支梁作为损伤识别研究的对象。该简支模型梁全长L=1000 mm,宽b=30 mm,高h=30 mm,弹性模量E=2.058×1011Pa,容重γ=7.86×107N/m3。
把梁划分为20个单元进行计算,编号为1~20,21个节点,简支梁模型如图1所示。

图1 简支梁有限元模型(单位:mm)
2.1 前期工作
以刚度的下降模拟结构单元的损伤程度,对于桥梁结构通常的损伤而言,结构刚度损伤超过50%时已失去其意义。
对于固有频率向量法,计算完好结构与各单元发生5%、10%、15%、20%、25%、30%、35%、40%、45%、50%损伤时的固有频率,从而形成损伤特征数据库。
对于特征值曲线交点法,在上述求得固有频率的基础上,求出每个单元在不同损伤程度下Δλi/Δλ1的均值。
2.2 损伤识别仿真
设置3个损伤单元,3种仿真工况如表1所示。仿真计算的目的为:①研究各方法损伤识别的能力;②比较各方法的优劣。
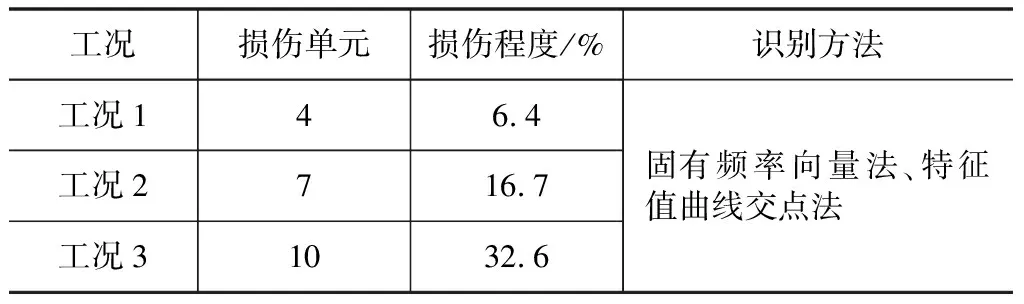
表1 损伤工况
3种仿真工况对应的前10阶频率值见表2。

表2 各工况对应的频率值
各工况对应的Δλi/Δλ1(i=2,3)的值见表3。

表3 各工况对应的频率平方变化比值
2.3 损伤识别结果
2.3.1 固有频率向量法
根据上述原理及计算步骤,MATLAB程序计算结果见图2~图4。
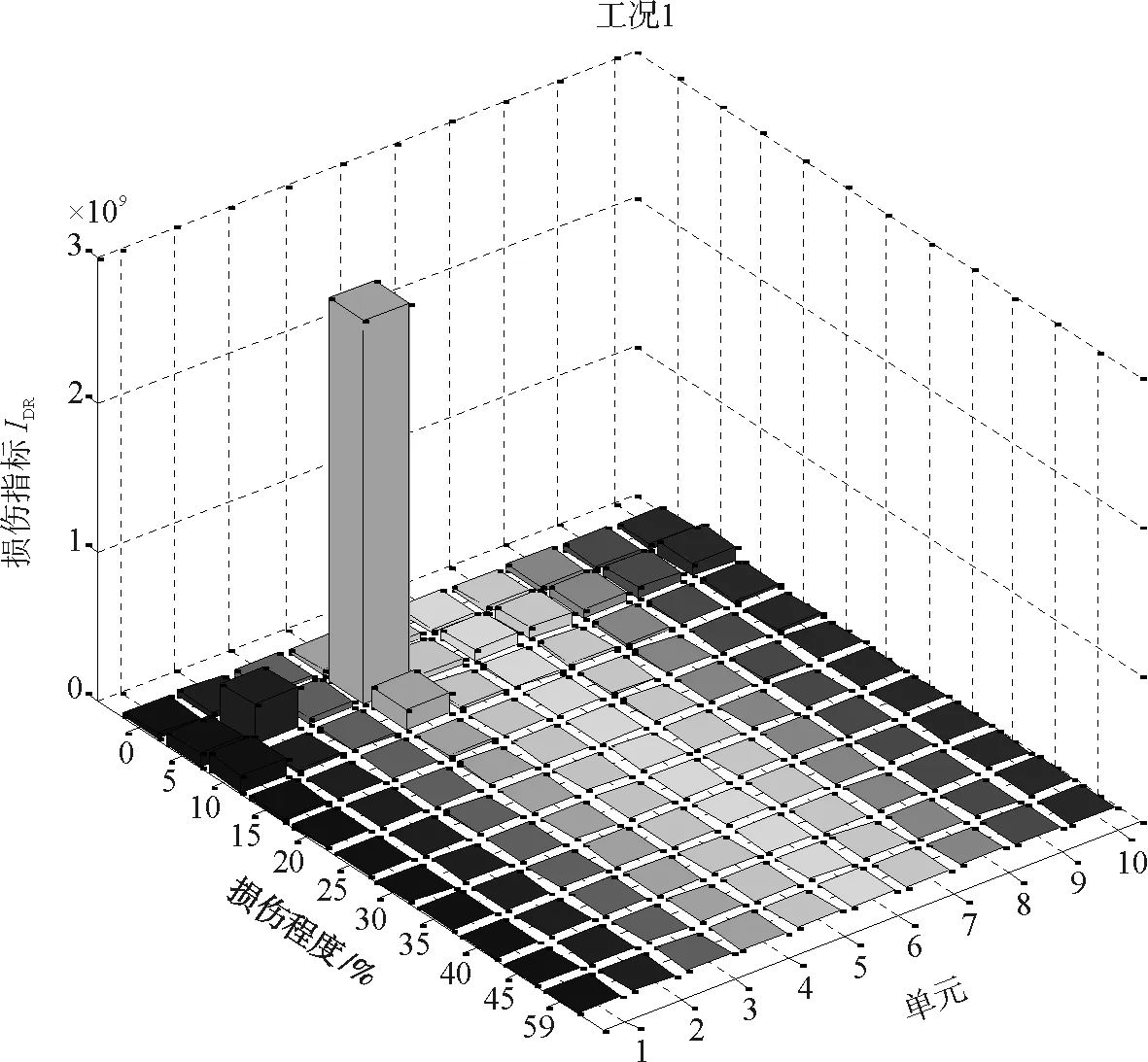
图2 工况1损伤识别结果

图3 工况2损伤识别结果

图4 工况3损伤识别结果
由图2~图4可知,各工况损伤位置能够精确识别,但由于损伤特征库中没有把所有可能损伤状态下的固有频率向量列出,对于本算例每隔5%才计算其固有频率向量,故两损伤状态中间的量不能精确表达,所以从各图中只能大致判断出损伤程度。图中判断出的损伤程度与实际模拟的工况的损伤程度还是很接近的,如工况1,损伤程度为6.4%,很接近损伤程度为5%的情况;工况3,损伤程度为32.6%,很显然其值介于30%~35%之间,且与两者的均值相差很小,故图4中30%与35%处柱状比较突出,这种情况可由两柱状的均值反推出大致损伤程度。
2.3.2 特征值曲线交点法
特征值曲线交点法计算结果如图5~图7所示;直线与曲线的交点处即为损伤位置,各工况损伤位置能够精确识别,但无法区分对称位置的损伤。且仅从图5~图7中无法直观估计出损伤程度,需另觅方法探测损伤程度。
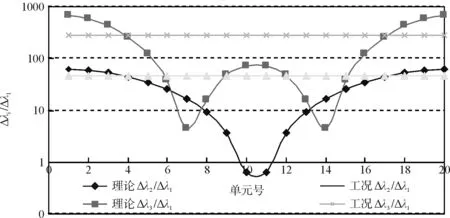
图5 工况1损伤识别结果
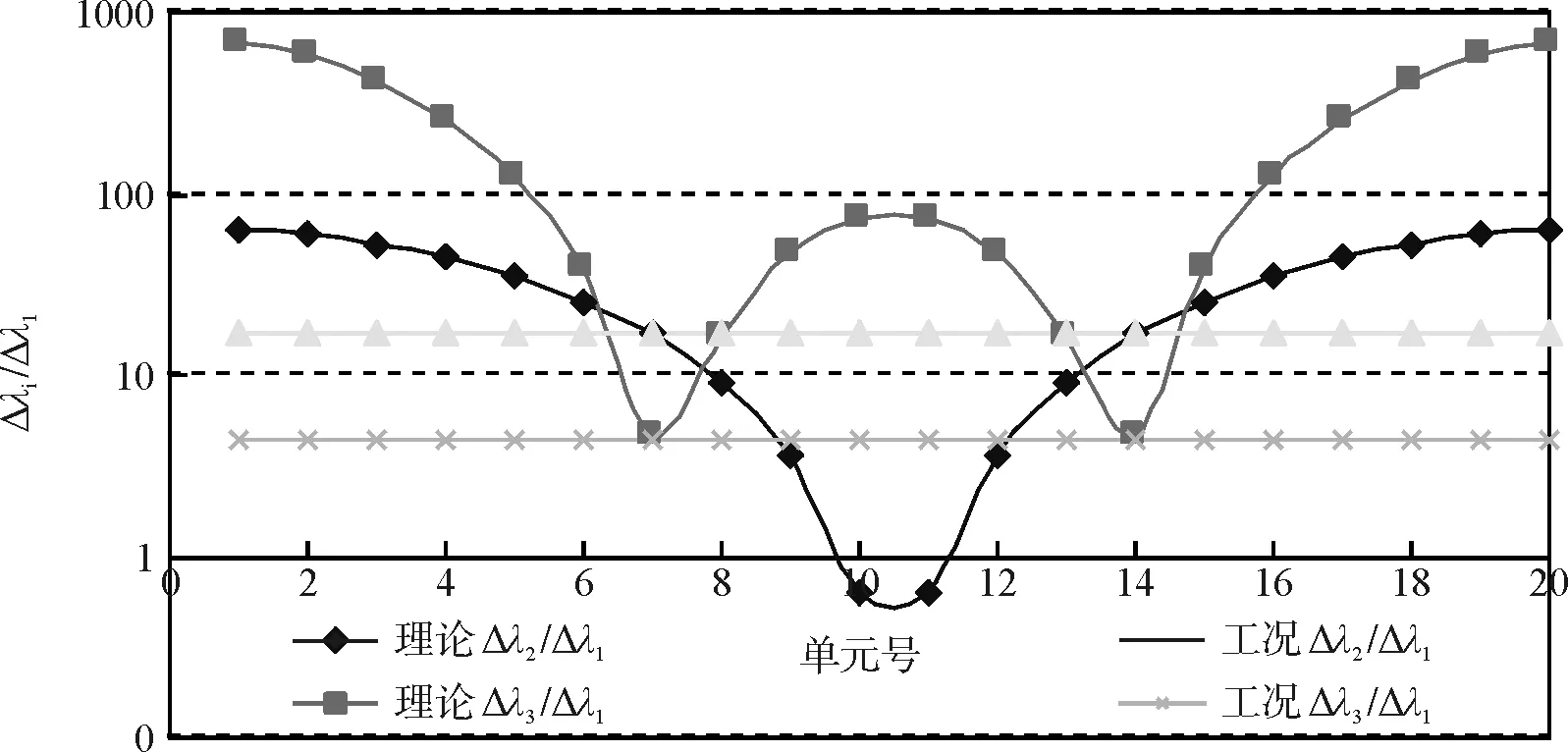
图6 工况2损伤识别结果
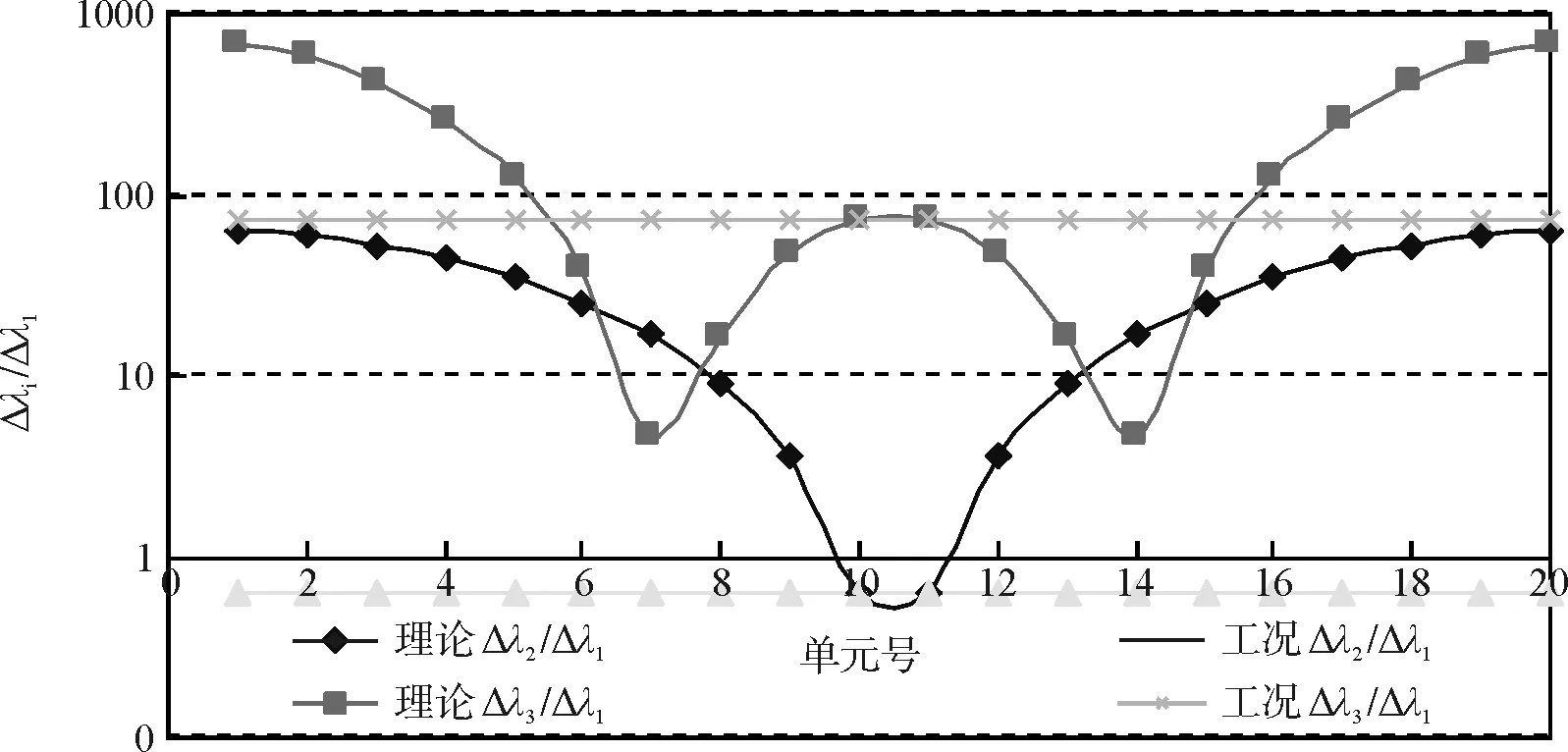
图7 工况3损伤识别结果
2.4 2种识别方法的比较
(1)损伤定位与程度识别方面:2种方法均可以精确识别损伤位置(对称位置除外,鉴于实际结构由于各种原因一般不会完全对称,故此方面不做重点考虑)。固有频率向量法可较准确的识别损伤程度,特征值曲线交点法无法识别损伤程度,这主要可从两者的基本原理上即可看出。
(2)计算量方面:固有频率向量法计算工作量大,需形成损伤特征数据库(损伤程度划分得越精细越好),且组成向量所需频率阶次较多,本文计算到了前10阶;特征值曲线交点法中,由于任意两阶频率平方变化比只是损伤位置的函数,和损伤的程度大小没有关系,故不需计算各损伤程度的值,只需要前2阶频率就可以进行评估,计算量相对较少。
3 结束语
(1)对于像桥梁这种具有分布参数的体系,由于自由度较多,利用固有频率向量法建立损伤特征库则是一个庞大的工程。该方法在单位置损伤识别时尚且不能把所有可能损伤状态下的固有频率向量列出,对于多位置损伤识别(多个损伤程度一致、多个损伤程度不一致) 其普遍适用性更有待后续工作的进一步研究。且如何使用较少的固有频率得到较优的识别结果也是一个亟待解决的问题。
(2)特征值曲线交点法计算量相对较小,但在利用交点定出损伤程度方面较欠缺。

