一个三元最值问题的探究之旅

2023-01-02 06:51深圳市龙华区教育科学研究院附属外国语学校518109钟文体

中学数学研究(广东) 2022年23期

关键词：表达式情形最值

深圳市龙华区教育科学研究院附属外国语学校(518109) 钟文体

文[1]刊有如下问题及其解答:

问题(《数学通报》2020 年2 月号问题2530) 已知a,b,c ∈[−2,2],a+b+c=0,求a3+b3+c3的最大值.

原解答通过构造一个特殊函数求得最大值,构思十分巧妙,但也有一定的局限性,不适用于一般情形.文[2-3]循原解答的思路,对上述问题作了一些扩展,但讨论较为复杂,不易把握.本文站在不同的视角,尝试探索新的解法.

一、问题新解

推广问题设a,b,c ∈[m,n],a+b+c=p(3m

文[2-3]在假定m,n,p满足一定条件的情况下,探究了a3+b3+c3的最大值,但过程比较曲折,且不易推广.出于对数学简洁美的追求,自然会问: 是否有更简洁明了的方法?

先看最简单的情形.当m≥0 时,根据幂平均值不等式容易求出最小值.事实上,即a3+b3+c3≥,等号成立当且仅当a=b=c=.但其它情形无法采用上述方法.

为了进一步解决问题,我们基于函数的观点,动态地看待上述问题.考虑三元函数F(x,y,z)=x3+y3+z3,其中x,y,z ∈[m,n]且满足约束条件x+y+z=p.那么,推广问题就转化为三元函数在约束条件下的最值问题,这类问题已经有成熟的求解策略(可参阅大学数学系的《数学分析》或理工科的《高等数学》),但超出了中学数学的知识范围.能否只用中学数学知识求解呢? 答案是肯定的,为此,需要对问题进行“降维”.

首先,根据x+y+z=p可消去一个变量,根据对称性,不妨消去z,将z=p −x −y代入,则只需考虑二元函数f(x,y)=x3+y3+(p −x −y)3((x,y)∈D)的最值即可,其中D={(x,y)|m≤x,y,p −x −y≤n}.此时,问题降了“1 维”,我们的目标是再降“1 维”,将原问题转化为一元函数最值问题.为此,我们采用各个击破的策略.先固定一个变量,例如x,将其看作常量,那么原问题就转化为关于y的一元函数问题,求出此时的最大值和最小值,它们与x有关,即为关于x的一元函数,再求出这些一元函数的最值即可.

明确策略后,下面进行具体操作.考虑关于y的函数fx(y)=x3+y3+(p −x −y)3(y ∈[m,n]),根据立方和公式可知

因此,只需考虑关于y的二次函数

类似前面,

但是,还有一个问题有待讨论,即以上7 个点是否满足问题的条件? 也就是说,这7 个点的坐标分量是否都在区间[m,n] 内? 这一问题等价于是否点R′(m,m)、点S′(m,n)、点T′(m,)、点U′(n,n)、点V ′(n,)、点W′()、点X′(−p,p)都在区域D内? 回答是否定的.例如,当p <2m+n时,点S′不在区域D内,如图1 所示(l1和l2分别表示直线x+y=p −n和x+y=p −m),对于不同的p,区域D的形状有3 种典型的情形,如图1-3 的阴影所示.

图1

图2

图3

注易知对任意p ∈(3m,3n),点W()总满足问题条件,即3 个分量都在区间[m,n]内.

根据以上分析,可以提炼出推广问题的求解策略.

策略在R′,S′,T′,U′,V ′,W′,X′中找出属于区域D的点,将找出的点代入函数F(x,y,z),从所得的函数值中找出最大值和最小值,即为推广问题的最大值和最小值.

二、实例

我们用以上策略来求解几个具体的问题.

例1([1] 的问题) 此时m=−2,n=2,p=0,容易验证此时只有T(−2,1,1)、V(2,−1,−1)、W(0,0,0)满足问题条件.因此,最大值为23+(−1)3+(−1)3=6,最小值为(−2)3+13+13=−6,根据对称性可知当a,b,c中有1 个2和2 个−1 时取最大值,当a,b,c中有1 个−2 和2 个1 时取最小值.

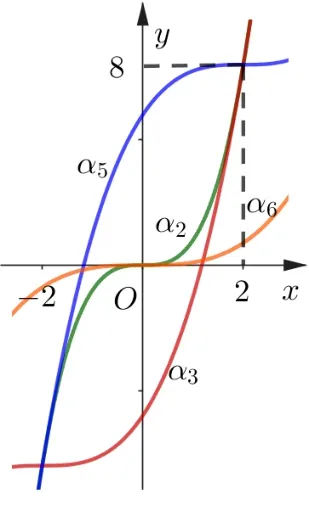
例2([3] 的命题) 已知a,b,c ∈[−2,2],a+b+c=p(−6

为了方便,当点P(r,s,t) 的每个坐标分量都在区间[−2,2]内时,称点P是可行点.易知,R(−2,−2,p+4)是可行点⇔p ∈(−6,−2];S(−2,2,p)是可行点⇔p ∈[−2,2];是可行点⇔p ∈(−6,2];U(2,2,p −4)是可行点⇔ p ∈[2,6);V(2,) 是可行点⇔p ∈[−2,6);W() 恒为可行点;X(−p,p,p) 是可行点⇔p ∈[−2,2].

将点R,S,T,U,V,W,X依次代入F(x,y,z),可得6 个表达式(S和X对应的表达式相同),如下表所示.