基于改进NSGA⁃Ⅱ算法的航班战略冲突解脱研究
徐 满,胡明华,张 颖,江 灏
(南京航空航天大学民航学院,南京 211106)
随着经济的不断发展,亚太地区将成为航空器客运量增长的主要动力,中国将在2022 年成为全球第一大航空运输市场[1]。由于空中交通需求的不断增长,当前的空域会变得越来越拥挤,空中交通的拥堵情况越来越严重。
航空器的冲突解脱问题是一个大规模组合优化问题,且由于航空器之间冲突的存在使得航空器之间相互耦合[2]。有大量的文献研究航空器在战术及预战术阶段的冲突解脱问题,主要通过调整航空器的起飞时刻、调整航空器的飞行速度、修改航空器的水平航迹和分配高度层等方式解决相应的冲突[3‑4]。但是,采用这些方式的短期内的冲突解脱存在一定的缺点,即没有从全局角度考虑航空器的冲突解脱。由于航空器之间的相互关系,短期内的冲突解脱可能会产生“多米诺骨牌”效应,使得冲突解脱一直处于被动,危及空域安全。例如,采用地面等待策略解决冲突时,已经延误了的航空器仍然需要继续等待其他航空器以满足空域的容量要求[5]。而战略冲突解脱研究,旨在根据航空器的飞行计划在起飞前相当长一段时间内解决潜在的飞行冲突,是确保航空器安全运行的一项关键技术。目前,战略冲突解脱问题引起了大量的关注。
四维航迹的运用以及基于航迹运行概念的提出被认为是未来空中交通管理的运行基础,在此基础上战略冲突解脱问题得到了进一步的研究。四维航迹将航空器航迹定义为三维空间加上时间,随着运行技术的不断发展,四维航迹可以有效降低航空器运行过程中的不确定性。这就为在一个较长时间范围内解决航空器之间潜在冲突提供了技术支持。
已有大量的文献研究了航空器四维航迹战略冲突解脱问题。冲突解脱由于问题本身的复杂度较高,常采用启发式算法求解,并且在提高算法的求解效率上做了大量的研究。2019 年,Dai 等[6]提出了一种改进的模拟退火算法,将求解过程分成两个阶段:第一阶段用于减少冲突数量;第二阶段用于优化航空器的飞行时间。同时,在冲突解脱时设计了一个均匀高度层策略,引导航空器均匀分布至各个可用高度层,引入滑动时间窗来降低问题复杂度以提高求解效率。但是其将冲突数量与航空器航迹偏移量进行线性组合,解决的仍是单目标优化问题。除此之外,还有大量运用模拟退火算法及其改进算法的研究[7‑9]。合作协同进化算法[10]在求解航空器冲突解脱问题也拥有良好的性能,合作协同进化算法采用分而治之的思想,将一个大规模组合优化问题分解成若干个子问题,从而降低问题的维数,各个子问题采用特定的进化算法优化得到部分可行解,通过各个小组之间的合作进化获取全局可行解。在合作协同进化算法的框架下,采用遗传算法进行优化可以极大提高算法的优化效率,其研究的仍是单目标优化问题。
在实际运行过程中,空中交通管制员往往会在冲突数量和航空器航迹调整量之间寻求一个很好的平衡,将冲突解脱问题建模为多目标优化问题更加 符 合 实 际。Su 等[11]于2017 年 采 用 多 目 标 文 化基因算法求解冲突解脱问题。算法采用经典非支配排序遗传算法(Non‑dominated sorting genetic al‑gorithm Ⅱ,NSGA‑Ⅱ)进行全局搜索获取可行解,同时结合局部搜索算法加强对当前最优解的搜索,获得更优可行解,但是算法的复杂度较高。多目标合作协同进化算法[12]同样被应用于冲突解脱问题,在协同进化算法的框架下,采用基于分解的多目标进化算法(Multi‑objective evolutionary algo‑rithm based on decomposition,MOEA/D)[13]进 行各个小组的内部优化。虽然采用了合作协同进化算法的框架,但是算法的求解效率较低。
针对以上问题,本文采用一种改进的NSGA‑Ⅱ算法研究航空器冲突解脱中的多目标优化问题,通过对算法内部遗传算子的设计,提高算法优化效率,同时控制算法的复杂度。在解决航空器之间潜在冲突的同时考虑与航空器航迹调整量所引起的航迹调整成本。本文采用调整航空器起飞时刻和分配高度层的方式在战略阶段解决航空器之间的潜在冲突,冲突成本来自航班冲突解脱后的飞行计划与初始飞行计划之间的偏差。主要创新之处在于,本文为染色体中的基因赋予相应的局部适应度,设计了一种自适应交叉算子与变异算子,结合NSGA‑Ⅱ框架进行全局优化。
1 问题建模
1.1 冲突探测模型
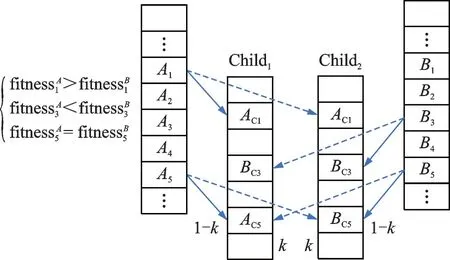
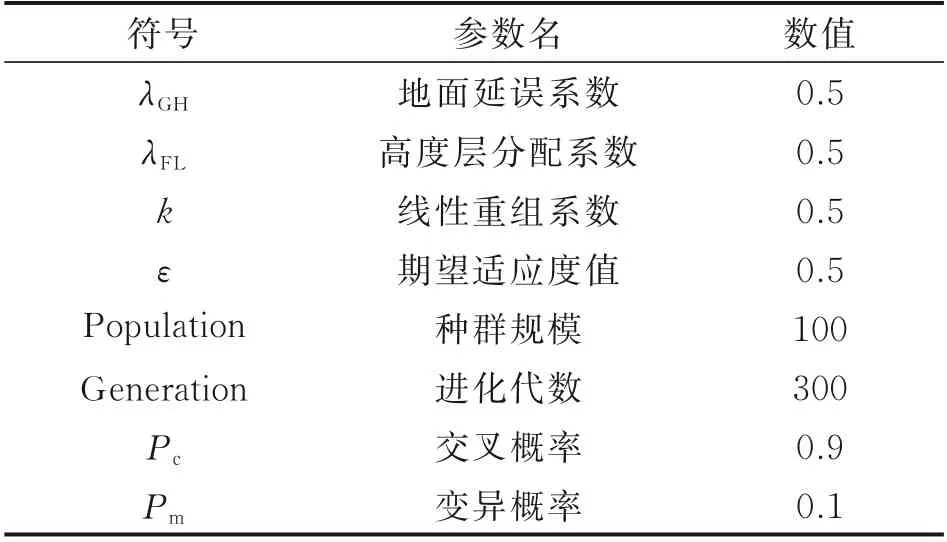
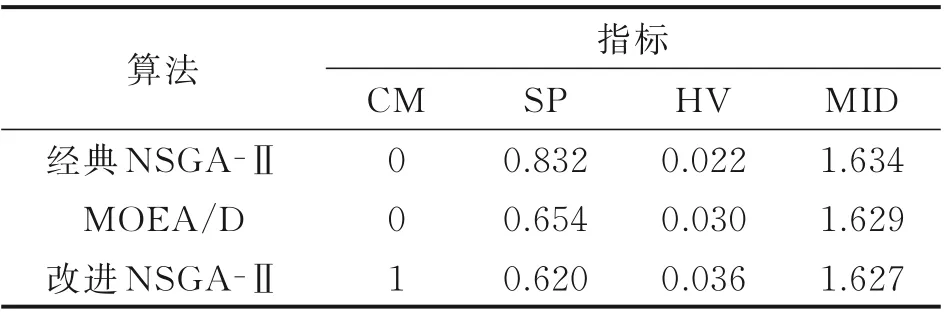
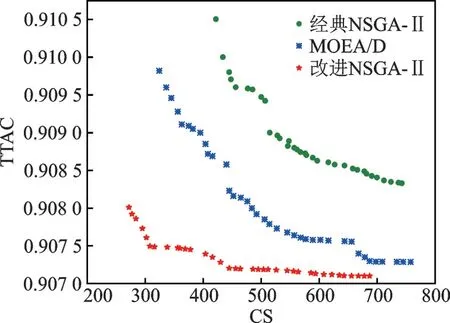
本文研究巡航状态下的航空器冲突解脱问题,因此假设航迹起终点为爬升和下降顶点。假设空域中有n架航空器,F=(f1,f2,f3,…,fn)按照航班计划沿着特定的航路飞行,航空器处于巡航状态,按照固定的高度层以恒定的速度运行。航空器的安全间隔在垂直方向上为Nv,水平方向为Nh,当航空器在空域中飞行时,它们的航迹相互影响。假设航班严格地按照计划航线飞行,那么潜在的冲突会发生在两条航路的交叉点附近,如图1 所示。当两架航空器的保护区发生重叠时,则认为两架航空器存在潜在冲突,这种情况并不意味着两架航空器一定会冲突,但是在运行过程中是需要避免出现的。当航空器fi和航空器fj的水平距离小于Nh且垂直距 离 小 于Nv时,‖Pfi(t)-Pfj(t)‖2 图1 航空器冲突图Fig.1 Aircraft conflict 为了表示航空器之间的冲突关系,本文定义了一个矩阵C来表示航空器之间是否有冲突,即 航路网络范围内的战略冲突解脱问题可以描述为:给定一个航路网络范围,对于航路网络中的每一架航空器进行四维航迹规划,在较低的航空器冲突解脱成本下尽可能减少航空器之间的冲突数量。在进行冲突解脱的过程中,应满足空域容量限制、航空器机动性能限制等。航空器f的航迹由一组四维航迹采样点组成,即有 1.2.2 目标函数 为保证航空器运行的安全性,必须尽可能地减少航空器之间的潜在冲突,由式(1)中的矩阵C可得航班之间的冲突关系。那么,航班fi的冲突数量可以由式(3)计算。 每一个冲突都被一对冲突航班重复计算两次,所以航班间的冲突数量为 在求解过程中,为了尽可能避免与其他航班之间的潜在冲突,可能对航班的初始航迹做出重大修改,从而导致大量偏移其初始航班计划。但是,这样的方式可能会产生额外的成本。因此,冲突解脱还应从经济角度进行评估,即航班应尽可能小地偏离初始计划,目标2 重点关注最小化航迹调整成本(Total trajectory amendment cost,TTAC)。本文采用调整航空器起飞时刻以及高度层分配解决航空器之间的潜在冲突,TTAC 由地面延误成本(CostGH)和高度层分配成本(CostFL)构成,那么目标2 可由式(5)计算。 式中:λGH为地面延误成本系数;λFL为高度层分配成本系数。由于地面延误成本与高度层分配成本单位不同,无法直接相加,因此需要进行归一化处理,即将每个航班的地面延误和高度调整量除以最大允许值。 (1)地面延误成本 航空器实际离场时间与初始飞行计划中离场时间之差为航空器的地面延误,即 式中lorig为航空器计划飞行高度层。 1.2.3 约束条件 考虑到安全性、公平性和航空器的性能,轨迹中的每个元素应尽可能接近其计划值。模型的约束集如下所示 ∀f∈F,e∈E,l∈L,t∈T均 应 满 足 上 述 约 束,E是航段集合。其中,约束(8)保证航空器沿着单一可行航线飞行;约束(9)保证航空器的地面延误不超出最大允许延误,TfGH表示单个航空器最大允许延误;约束(10)保证航空器的飞行高度层只能在允许的高度层内,NfFL为最大高度调整量。 多目标优化可以定义为寻找满足约束条件的决策变量向量,并同时优化多个目标函数的问题,目标函数之间往往是对立的。NSGA‑Ⅱ根据目标函数特点,对可行解进行非支配排序,最终得到Pareto 前沿。与经典的NSGA‑Ⅱ算法及MOEA/D 相比,本文采用的算法根据问题特点设计了自适应交叉算子与变异算子[15]加快进化过程。 2.1.1 初始化种群 本文采用调整航空器起飞时刻与高度层分配两种方式解决航空器间的潜在冲突,在生成初始种群时,根据当前航班计划中各个航班冲突数量,采用轮盘赌随机选择一条航迹,冲突数量越多,航迹被选中的概率越大。以概率形式随机修改起飞时刻与飞行高度层,独立运行N次,生成初始种群,具体过程如图2 所示。 图2 种群初始化流程图Fig.2 Flow chart of population initialization 2.1.2 选择 本文采用锦标赛选择法。从父代种群中随机选择两个父代,首先比较两个父代的非支配序,优先选择非支配序较低的父代个体;若父代的非支配序相同,则比较父代个体的拥挤距离,优先选择拥挤距离较大的父代个体。 2.1.3 交叉 本文采用的自适应交叉算子,在进行交叉操作时,对于选择的父代个体,比较父代个体相同位置基因的适应度,即在两个不同的航班计划中比较同一架航班在该计划下的冲突解脱成本。个体中每架航班的局部适应度由式(11)计算。 式中:AC和BC分别为线性重组生成的两个子代,floor 表示向下取整,k为线形重组系数,交叉概率为Pc。自适应交叉算子如图3 所示。 图3 自适应交叉算子Fig.3 Adaptive crossover operator 2.1.4 变异 较高的局部适应度意味着该航班的飞行计划产生较少的冲突和较低的飞行成本,所以当染色体某个位置基因适应度值小于ε时,才发生变异,其发生变异的概率为Pm。自适应变异算子如图4所示。 图4 自适应变异算子Fig.4 Adaptive mutation operator 如何评价冲突解脱优化解集的优劣,在使航班尽可能小地偏离初始飞行计划的情况下得到较少冲突数量的航班计划是一个值得深究的问题。本文拟从Pareto 最优解的收敛性和多样性两个方面进行评估,采用以下4 个指标[16]来评估本文提出的算法。 2.2.1 覆盖率 覆盖率(C‑Metric,CM)是衡量Pareto 前沿的收敛性的指标,即 式中PFU、PFV分别为两组Pareto 最优解集。分子表示解集V中被U中至少一个解支配的解的数目,分母表示解集V中所有解的个数。 若CCM(PFU,PFV)=1,说明解集V完全被解集U支配,即解集V收敛性比解集U差。 2.2.2 空间分布 空间分布(Spacing,SP)是衡量Pareto 前沿的广泛程度的指标,即 式中:up表示各个解到其他解的最小欧氏距离;-u为均值。CSP(PF)值越小,说明空间分布越均匀。 2.2.3 超体积 超体积(Hyper volume,HV)是衡量Pareto 前沿收敛性和多样性的综合指标,即 式中:δ代表Lebesgue 测度,用来衡量体积;Vp表示第p个点与参考点围成区域的超体积。超体积值越大,表示解集的效果越好。 2.2.4 平均理想距离 平均理想距离(Mean ideal distance,MID)是衡量Pareto 前沿和理想点间距离的指标,即 式中表示第p个非支配解的第t个目标值。本文研究双目标优化问题,因为求解最小化问题,所以理想点可设置为坐标原点。 本文重点研究巡航阶段冲突解脱问题,数据采用2019 年6 月8 日9:00 至12:00 中 国 航 路 网 络 中1 472 架航班进行仿真验证,在MATLAB R2019a平台上运行,航班飞过的航路点如图5 所示,涉及2 136 个航路点和186 个起降机场。本文对每条航迹采用等时间间隔采样生成相应的航迹采样点,采样间隔为15 s,利用墨卡托投影将航迹采样点从经纬度坐标转化为(x,y)坐标。允许的单个航班最大延误TfGH为60 min,航班离场时隙为1 min;单个航班飞行高度最大调整量NfFL为1 200 m,遵循“东单西双”的原则,允许的飞行高度范围为8 900 m至11 600 m,以300 m 的间隔划分高度层。采用网格法探测航空器之间的潜在冲突,网格在水平方向上大小为Nh,在垂直方向上为Nv,时间维度的网格大小与采样时间间隔相等。本文采用的改进NS‑GA‑Ⅱ算法各项参数如表1 所示,其中,种群规模与进化代数等参数均通过多次对比实验得到的最优结果确定。 图5 航路点图Fig.5 Distribution of waypoints 表1 算法参数设置Table 1 Parameter settings of algorithms 3.2.1 算法性能评价 本文将改进的NSGA‑Ⅱ算法与经典NSGA‑Ⅱ算法以及MOEA/D 进行对比验证算法的有效性,同时利用多目标优化解的指标进行评价,具体结果如表2 所示。启发式算法的优化效果具有随机性,因此,表2 中的结果均基于15 次独立重复试验得到。 表2 算法性能对比Table 2 Performance comparison between algorithms 由表2 可知,改进的NSGA‑Ⅱ算法在各项性能上均优于经典的NSGA‑Ⅱ算法及MOEA/D。覆盖率指标,改进的NSGA‑Ⅱ算法得到的Pareto前沿完全支配另外两种算法。改进的NSGA‑Ⅱ算法的Pareto 最优解相对于经典算法及MOEA/D而言,解集更占有支配地位(CM),解集的分布更均匀(SP),解集的收敛性更好(HV),解得质量也更高(MID)。 算法的收敛性和多样性可由反转世代距离(Inverted generational distance,IGD)反映,本文将15 次独立运行得到的Pareto 最优解集P*作为参考集,计算参考点到最近的解的距离的平均值。IGD值越小,说明算法综合性越好,即 IGD 值与进化代数的关系如图6 所示,由于IGD 值在前100 代平稳,所以图中只选取了前100代的结果并做归一化处理,以使变化趋势更加明显。 图6 IGD 变化趋势Fig.6 IGD changing trend 由图6 可知,在当前参数条件下,3 种算法均可收敛。在3 种算法中,采用了自适应遗传算子的改进NSGA‑Ⅱ算法收敛速度最快。表3 给出了3 种算法在达到收敛代数和达到最大进化代数时的运行时间。对比MOEA/D 算法、经典NSGA‑Ⅱ算法与改进的NSGA‑Ⅱ算法,本文所提算法在运算速度上提高了约8%。 表3 算法运行时间对比Table 3 Running time comparison between algorithms 3.2.2 算法优化结果 图7 是3 种算法的优化结果对比图。由图可知,改进的NSGA‑Ⅱ算法不仅在冲突解脱的效果上优于两种算法(Obj1),而且产生的航迹偏移量(Obj2)也更小。在最终的Pareto 最优解集中,本文的改进算法目标1 最优时可以将冲突数量减少至272,而经典的算法冲突数量则多达422,MOEA/D冲突数量最小也为324 个,这反映了在引入改进了的交叉算子和变异算子后算法在冲突解脱方面的优异性能。目标2 则反映出改进后的NSGA‑Ⅱ算法,在解决冲突的时候产生的航迹调整量更少,使航空器在冲突解脱时产生更小的调整成本,符合航空公司的利益。 图7 Pareto 前沿对比图Fig.7 Comparison chart of Pareto front 本文主要研究了冲突解脱中的多目标优化问题。针对问题的特点,本文将航空器冲突解脱建模为以冲突数量和航空器航迹调整量为目标的双目标优化问题。针对所求解的冲突解脱问题的特点,采用了一种改进的NSGA‑Ⅱ算法,设计了自适应交叉算子与变异算子,旨在提高算法搜索最优解的效率。与经典的NSGA‑Ⅱ算法以及MOEA/D 相比,改进了的算法具有冲突解脱的有效性和求解的高效性,不仅可以同时兼顾航迹调整成本解决大量冲突,而且能更快收敛,有很强的参考价值。 下一步的工作主要集中对更复杂冲突解脱方式的建模以及进一步提高算法的效率上:冲突解脱方式除了考虑起飞时间和高度层优化分配,还可以考虑航迹的水平调整以及高度层的分航段优化;算法在求解大规模航班时缺乏时效性,可能需要大量的计算时间。采用更加多样化的冲突方式和将算法与局部搜索算法相结合以提高搜索效率预期将有助于提高算法的效率。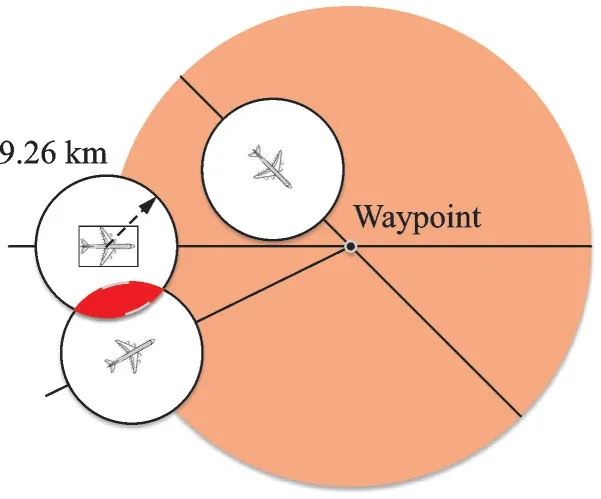

1.2 数学优化模型

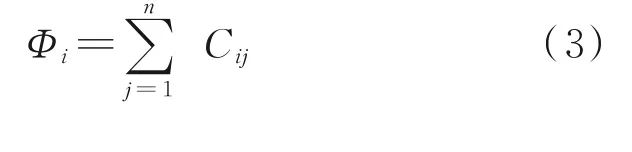

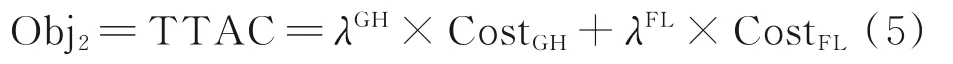


2 多目标优化算法设计
2.1 改进的NSGA⁃Ⅱ算法



2.2 多目标优化解的评价

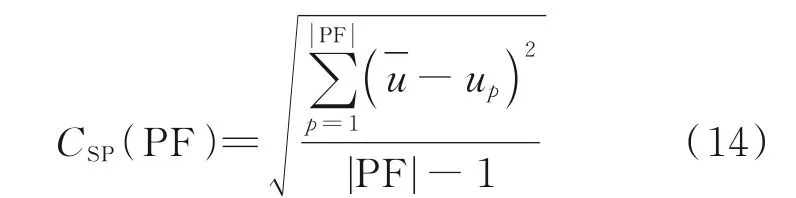
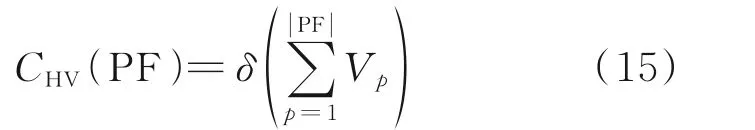
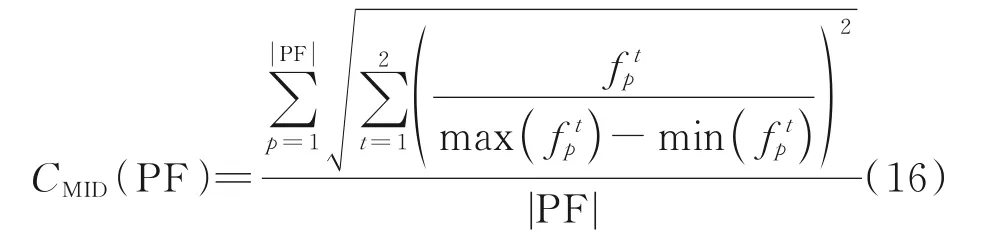
3 仿真验证
3.1 运行场景

3.2 结果分析
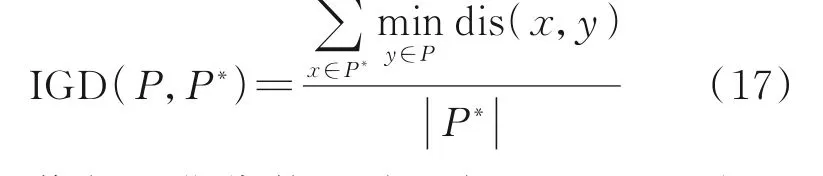


4 结 论
——基于人力资本传递机制
——基于城郊农村的调查
——基于反向社会化理论的实证研究

