基于短暂丢失参考信号预测的无人直升机轨迹跟踪控制

杨静雯，李 涛，杨 欣，费树岷

（1.南京航空航天大学自动化学院,南京 211106；2.东南大学自动化学院,南京 210096）

无人机发展过程可追溯至20 世纪初，20 世纪50 年代开始快速发展，并在后来几次局部战争中崭露头角，逐步成为新型的空中作战与运输平台。无人机按照气动原理可分为固定翼无人机和旋翼无人机。与固定翼无人机相比，旋翼无人机，即无人直升机（Unmanned aerial helicopter，UAH），虽然控制难度较大，但具有很多独特优热，例如垂直起降、定点悬停、原地转弯、低空飞行、侧飞后飞，能利用复杂地形隐蔽飞行等。这些特殊飞行方式不仅使UAH 完成固定翼无法完成的任务，也使其具有较好灵活性，可有效执行某些特殊的军事任务。然而，由于UAH 系统具有高度非线性、强耦合、开环不稳定及欠驱动等特性，且飞行中易受到各种扰动影响，设计高性能飞控算法是具有挑战性的难题［1］。近年来，许多控制方法被用于UAH 系统的控制器设计［2⁃3］，包括鲁棒控制、神经网络控制、预测控制、滑模控制、自适应控制、反步控制、最优控制等。在UAH 控制目标中，跟踪控制应用较为广泛，包括自主着舰、吊装运输、空地协同等。因而UAH 跟踪控制成为研究热点并取得许多优秀结果［4⁃6］。例如，文献［7］针对UAH 非线性和强耦合等特性，提出基于动态反馈线性化方法的鲁棒跟踪控制策略；文献［8］基于状态受限设计鲁棒动态面控制器，并将UAH 系统解耦为平移系统与旋转系统以完成跟踪控制；文献［9］同时考虑UAH 速度跟踪与偏航角跟踪，利用滑模控制补偿俯仰角不可测的不利影响；文献［10］将UAH 模型分成3 个子系统，随后设计自适应反步控制器实现位置和偏航角跟踪控制；文献［11⁃12］分别基于非线性和线性模型预测控制设计UAH 抗扰跟踪控制器；文献［13］建立基于分层架构的模型预测轨迹控制设计方案。

需要指出的是，实际UAH 对地目标跟踪过程中可以通过全球定位系统（Global positioning sys⁃tem，GPS）获得地面参考目标轨迹信息，但复杂外部环境或未知扰动会导致参考信号不能被实时获取［14］。UAH 无法实时获取参考目标运动轨迹，从而造成跟踪控制性能下降甚至任务失败。但目前关于短暂丢失参考信号下UAH 跟踪控制研究结果较少，难点在于如何对丢失信号进行有效预测并加以利用。而在船舶轨迹定位中，文献［15］将短暂丢失轨迹信息分为平稳序列和非平稳序列信号分别进行预测估计；文献［16］利用强跟踪扩展Kalman 滤波算法和传统Kalman 滤波算法对丢失信号切换预测；文献［17］利用移动平均自回归（Auto⁃regressive integrated moving average，ARI⁃MA）模型获得残差并传给长短期记忆模型以提取数据中非线性特征，集成后获取最终预测结果。然而文献［16］中研究方法虽然能降低计算量，但预测模型单一且精度较低；文献［17］预测方法易受不确定性影响，算法鲁棒性较弱。而在信号处理领域中，文献［18］利用ARIMA 模型对通讯系统中随机传输时延进行预测；文献［19⁃20］借助马尔可夫分析法构建间歇信号发生后的预测模型。

根据现有成果和实际UAH 跟踪情形，本文考虑复杂环境下受到外界扰动影响，存在地面参考目标信号短暂丢失下的无人直升机空地协同跟踪问题，其中UAH 与地面运动目标呈自然式轨道构型。首先，将短暂丢失的参考信号分解为趋势序列和不规则变化序列两类信号，并对文献［18⁃20］中方法加以改进，从而实现对丢失参考信号的准确预测，以有效提升预测精度和控制算法的鲁棒性。然而，引入预测机制会增加UAH 控制系统的设计难度和控制计算量。根据文献［21］结果，滑模控制无需设计干扰观测器便可抑制部分外界干扰对控制性能的影响，但文献［22］指出采用基于趋近律的滑模变结构控制方法难以消除抖振现象。因而本文针对UAH 跟踪控制目标，对文献［22］方法进行改进，建立了由饱和函数构建的自适应滑模趋近律［23］以有效减小抖振现象，同时引入有限时间限制条件以提升对地目标的跟踪效率［24⁃25］。

本文主要创新性总结如下：

（1）根据短暂丢失参考信号的特性及可利用信息，考虑其平稳因素与非平稳性因素并分别构建短时预测模型，改进现有的ARIMA 模型并基于马尔可夫分析法引入状态迁移矩阵，从而对短暂丢失的地面参考信号进行准确且高效的预测。

（2）利用滑模控制技术设计控制器以抑制干扰影响，在趋近律中引入幂函数，能有效避免输出超调并能在跟踪误差系统产生强烈抖振的前提下快速收敛至滑模面。同时，为进一步减小抖振现象，在趋近律中引入自适应饱和函数，从而能增加控制系统设计的灵活性和鲁棒性性。

文中变量定义：R 表示实数集；Rm×n表示m×n实数矩阵集；|x|表示将矩阵x内所有元素分别绝对值化；‖ ‖x表示向量x模；x͂表示将向量x中元素化为对角矩阵；AT表示矩阵A转置；Sym {A}表示矩阵A+AT；A/B表示矩阵（向量）A中元素除以矩阵（向量）B中对应的元素。

1 无人直升机系统模型

由于实际UAH 系统模型具有高度非线性［21］，为了方便叙述后文控制设计方案，基于文献［21］模型简化方法，可获得如下的UAH 线性系统模型

2 跟踪参考信号模型

UAH 对地跟踪过程中，如果地面目标运动轨迹能够实时获取，则可以直接利用其参考信息获得跟踪误差信号，并完成相应的控制设计方案。但若由于地形复杂等因素导致参考信号短暂丢失，则假设此时地面信号受到随机扰动影响，且该轨迹信号同时具有趋势平稳特征和非平稳特征。针对短暂丢失的部分信号，如果采用单一算法建立预测模型，则会产生与实际信号较大的预测误差。因而本文在地面坐标系下针对文献［15］中预测模型加以改进，以已知的地面目标位置信息为样本，将ARI⁃MA 算法和马尔可夫分析法结合获得改进后的预测模型，能实现对地面目标信号丢失后的未知位置信息进行有效预测，从而在一定程度上解决时间序列预测双重特征带来的预测精度不高等问题。

2.1 平稳参考信号模型

根据已有研究结果［13］，趋势平稳特征下的ARIMA 预测模型，通常包括移动平均（Moving av⁃erage，MA）过程、自回归（Autoregressive，AR）过程、自回归移动平均（Auto⁃regressive moving aver⁃age，ARMA）过程和差分整合ARIMA。本文将其分解为如下步骤，建立改进后的ARIMA 预测模型：

（1）获取参考信号未丢失时地面目标运动轨迹的定位数据。

（2）针对所获取的数据绘图，观测其是否为平稳时间序列；如果是非平稳序列，则对其进行d阶差分运算后转化为平稳时间序列h(t)。

（3）计算上一步所得到的平稳时间序列自相关函数（Auto⁃correlation function，ACF）和偏自相关函数（Partial correlation function，PACF），并通过对定位数据图像的分析，获得最佳的阶层p和阶数q。

（4）基于上述步骤中所获取的d、p、q，建立ARIMA(d，p，q)模型，并进行模拟预测观察，确定是否符合已有数据特征，若不符合则重新确定阶层p和阶数q。

定义1 平稳序列下ARIMA 预测模型［17］如下

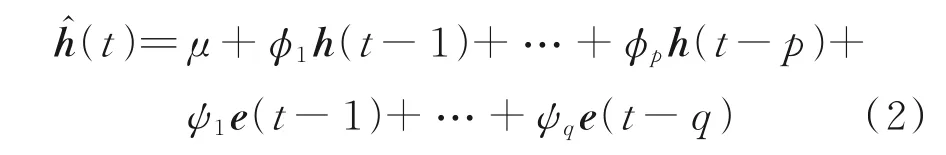
式 中：ϕi(i=1，2，…，p) 为AR 的 系 数；ψi(i=1，2，…，q)为MA 的系数；ĥ(t)为当前平稳趋势数据序列的预测值；e(t-i)(i=1，2，…，q)为最新预测误差；μ表示初始值。

由定义1 可知，经过差分运算后时间序列将在某常数附近波动且变化范围有限，并存在延迟k的平稳序列。序列平稳性通常可利用图检验法和单位根检验法进行测试。而在ARIMA 模型中存在如下函数

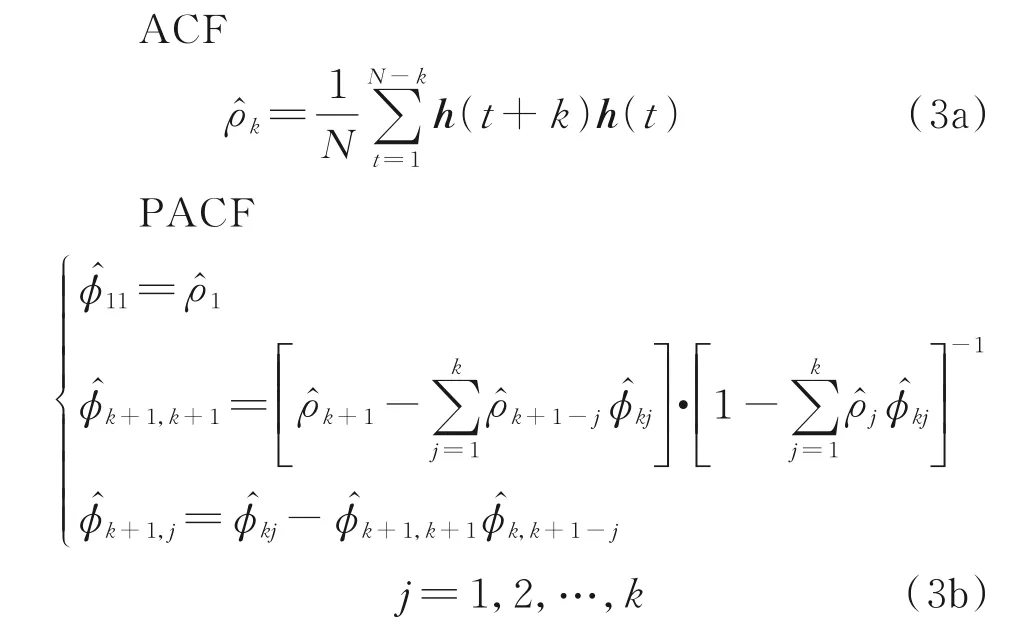
依 据ARIMA(p，q)模 型 中ACF 和PACF 函数，可以得到自相关图和偏自相关图，从而确定用AR(p)模型，MA(q)模型还是ARMA(p，q)模型，并由截尾与拖尾阶数确定预测模型中采用的时序数据的滞后数p和预测模型中采用的预测误差的滞后数q。为了检验参考轨迹样本中趋势信息是否已被完全提取，可采取分位数图（Quantile⁃quantile plot，QQ⁃plot）方法或杜宾⁃瓦特森检验（Durbin⁃Watson，D⁃W）方法对残差进行检验，判断残差是否满足正态分布，连续残差是否存在自相关性。如果残差是白噪声序列，则平稳序列h(t)中有用的信息已经被提取完毕，余下信息是无法预测和使用的随机扰动。若残差不是白噪声序列，则需进一步修改或重新定义预测模型。

当上述预测模型检验合格之后，就可以在当前参考轨迹数据样本上，对短暂丢失信号的参考目标运动轨迹进行实时预测。需要指出的是，ARIMA预测模型也存在问题，首先模型建立需要大量历史数据的支撑，当地面目标运动轨迹可利用的参考数据较少时，会影响信号短暂丢失后预测精度，甚至导致模型建模失败；其次，虽然ARIMA 模型能对远超测试集时长的参考信号进行预测，但随着预测时间增加，预测方差会随之增加，预测精度也会降低，所以ARIMA 方法在实际应用中并不适用于长时预测。

2.2 非平稳参考信号模型

本文将丢失参考信号中非平稳序列部分定义为受到随机扰动影响的运动轨迹，并通过均值漂移聚类方法构建预测误差的马尔可夫分析法模型，用以修正预测模型。

首先，在当前参考轨迹样本的基础上，获得该参考样本与参考样本预测数据的差值g(t)。其次，采用均值漂移聚类算法对预测误差分组定值。均值飘移聚类算法是一种基于非参数概率密度梯度估计的迭代过程，根据形心和迭代来精准定位并优化每组的定位点，用以发觉预测误差数据信息值的重点区域。较之参考文献［15］中采用的k均值聚类算法，均值漂移算法不需确定分类总数，该算法会自动识别出数据的中心数量，且聚类中心不取决于最初假定的中心点，划分相对稳定，适用于由随机扰动造成的预测误差聚类。均值漂移聚类算法过程如下：

（1）在未被标记的数据点集中，随机选择一个点作为假定的中心点；

（2）计算窗口内数据点均值，然后将窗口中心点由假定中心平移至均值点；

（3）重复步骤（2）直到平移值小于设定的阈值即迭代收敛，在这一过程中窗口内经过的所有数据点都属于该中心点组；

（4）重复步骤（3）直到所有数据点均被访问过；

（5）如果收敛时当前组的中心点与其他已经存在的组中心点的距离小于阈值，则把这两个组合并；否则，将当前组作为新的组；

（6）最终划分出n组预测误差组，并分别记作ϵk(k=1，2，…，n)，将每组对应中心点值记作γk。

接下来，按照划分后各组的数据点数及中心点值求得预测误差的马尔可夫转移概率。在任何给定时刻、当前状态以及所有过去状态的情况下，UAH 系统所受随机扰动的未来状态条件概率分布仅依赖于系统当前状态，即满足马尔可夫性质，因而可采用马尔可夫分析法进行处理。

定义2 马尔可夫分析法的基本模型［15］为

式中：X(k)表示趋势分析与预测对象在k时刻的状态向量；X(k+1)表示趋势分析与预测对象在k+1 时刻的状态向量；P表示转移概率矩阵。

接下来建立马尔可夫分析法模型。 首先计算转移概率矩阵。将当前数值点所在的组ϵi(i=1，2，…，n) 经 过 一 步 转 移 后 到 达 组ϵj(j=1，2，…，n)的次数记为Σ(ϵj|ϵi)，将组ϵi出现总次数记为Σ(ϵi )，则由转移概率组成的状态转移矩阵为

式中：P（t）为随时间改变的矩阵，通过式（5）确定不同时间下p的值；ϵi(i=1，2，…，n)中n的数量随时间增加而增加。

因此可以建立预测差值数据的马尔可夫分析法修正预测序列为

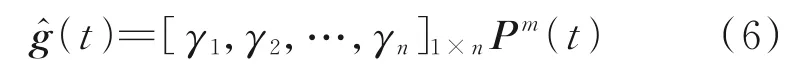
式中ĝ(t)表示预测误差序列g(t)的m步预测值，当m=1 时，ĝ(t)为当前时间点的预测误差值。结合定义1 和式（6）可以建立信号丢失部分的优化预测 模 型f(t)=ĥ(t)+ĝ(t)，其 中ĥ(t)为 平 稳 趋 势特征下ARIMA 预测模型，而ĝ(t)代表非平稳特征下关于预测误差的马尔可夫分析法的修正模型。

3 控制律设计

基于第2 节中所获得的地面坐标系下参考目标的预测运动轨迹，可以得到地面目标的定位信息序列。并由序列时间间隔通过差分或求导的方式得到在参考信号短暂丢失时间段内实现跟踪目标所需的同坐标系下参考速度序列。随后将已知地面目标速度序列与预测所得速度序列组合得到横纵向与垂直向完整的速度序列。最后通过跟踪要求与UAH 机体姿态信息将完整的参考速度序列转换至机体坐标系中，构成跟踪所需参考信号Ur(t)与wr(t)。考虑到滑模控制技术能有效抑制外部干扰的影响，本节将UAH 系统（1）分为纵向⁃横向子系统和垂直子系统［21］，并在此基础上分别给出纵向⁃横向子系统和垂直子系统的跟踪控制器设计方案。

3.1 纵向‑横向子系统控制律设计

首先定义跟踪误差e1(t)=Ur(t)-U(t)，为了设计满足跟踪性能的UAH 控制器，对跟踪误差进行求导并结合式（1）可得到e2(t)

但由于地面移动目标参考信号的特性，趋近律中需要引入快速滑模成分，以提高跟踪速度并减小跟踪误差，即

式 中 系 数Cuv、F1、F2、F3∈R2×2为 给 定 的 常 数 矩阵。接下来，对式（10）进行求导可得到滑模面的导函数如下

考虑滑模控制具有较强鲁棒性，控制器设计将不包含干扰项但将其保留在趋近律中，闭环系统稳定性分析将在后文证明过程中给出，而控制器设计如下

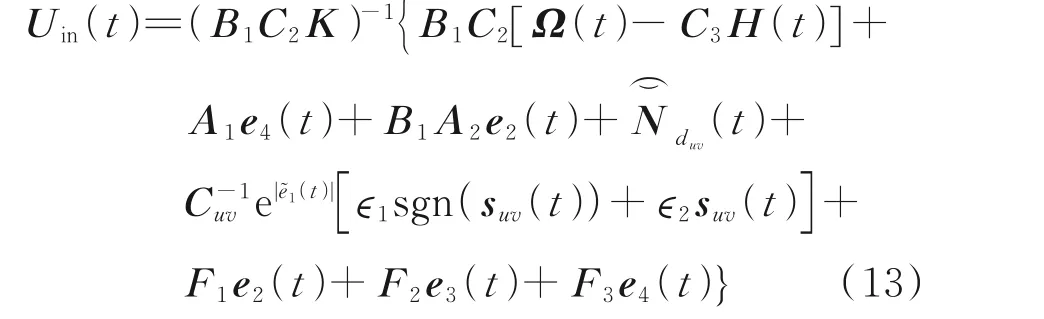
式中系数B1、C2和K均为已知二阶常数矩阵，并满足矩阵B1C2K可逆，这里取ϵ1、ϵ2为待确定的非负常数。

3.2 垂直子系统控制律设计

针对垂直子系统设计控制器，首先定义跟踪误差ew(t)=wr-w(t)，则

式中：系数Zcol为非零常数；ϵ3、ϵ4为待确定的非负常数。

3.3 稳定性证明

定理1 根据地面目标运动轨迹可用信号和丢失信号的预测信息，给定任意正定矩阵M1、正数m2，利用跟踪误差设计控制器如下

当选取的横向⁃纵向子系统和垂直子系统控制参数同时满足条件ϵ2、ϵ4>0 与式（17b）时，则跟踪误差系统可在有限时间内趋于稳定，即UAH 能实现对地面目标的期望跟踪

再对上述不等等式进行缩放，可以得到

由于Lyapunov 稳定性第二方法所需条件无法确定跟踪误差系统收敛的最大时间，可能会出现较长时间才能收敛至零的问题，这样的控制器在应用中没有太大实际意义，在下面步骤中将对稳定性证明条件进行完善。

最后，可以得到垂直子系统跟踪误差渐近稳定的限制条件

综合式（25b，26c）即可证定理1 成立。

3.4 控制设计改进

滑模控制容易产生抖振现象，抖振幅过大会影响实际UAH 控制系统的跟踪性能，甚至会导致跟踪误差系统不稳定。为了缓解抖振不利影响，可以将趋近律中常用的符号函数替换为饱和函数。但这样会影响控制速度与控制精度。通常而言，抖振越大控制系统反应速度越快，但精度很差；抖振小，精度高，但反应速度会变差，所以趋近律设计要引入跟踪误差因素，将趋近律改进为自适应饱和函数趋近律，可使本文所提滑模控制设计具有自适应特点。主要包括：

（1）改进后横⁃纵向子系统趋近律为

由于Δuv(t)，δw(t)取值大小会影响抖振程度，所以将其设置为与跟踪误差相关变量Δuv(t)=e-e1(t)，δw(t)=e-ew(t)，这 样 当 跟 踪 误 差 较 大 时，UAH 系统会牺牲精度而提升跟踪效率，而当跟踪误差较小时，UAH 空地协同控制系统则会偏重于跟踪精度而非速度。

4 仿真验证

本节针对UAH 空地协同跟踪系统（1）进行数值模拟，以验证本文所提控制算法的有效性。

当Y=0 时参考信号正常接收，当Y=1 时参考信号丢失。取与非季节性AR、MA 多项式系数相关的滞后和差分次数分别为1，与季节性AR、MA 多项式系数相关的滞后选取为4，季节差分多项式的度为24。

将预测误差分为10 类，横向子系统和纵向子系统的预测误差概率转移矩阵为

对应的聚类中心

随后利用文中滑模控制器设计方法，取滑模面参 数F1=81I，F2=27I，F3=9I，Cuv=0.01I。设定趋近律参数ϵ1=10，ϵ2=0.1，其他参数分别选取为M1=I，m2=1。

图1，2中蓝色部分为参考目标运动的实际轨迹，红色部分为根据参考数据所得到的信号短暂丢失下预测模型。由图1可见，相比于采用单一预测模型进行预测，加入马尔可夫分析法模型进行修正后的预测轨迹更加贴近实际轨迹，且预测性能也有较大提升。

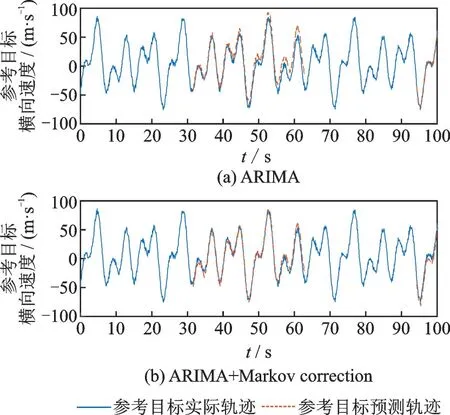
图1 横向子系统ARIMA 预测及修正后结果对比Fig.1 Comparison of ARIMA prediction and correction results for horizontal subsystem

接下来，选取ϵ1=10 和ϵ2=0.1 通过改进后滑模控制设计并得到跟踪仿真结果，如图3，4 所示。

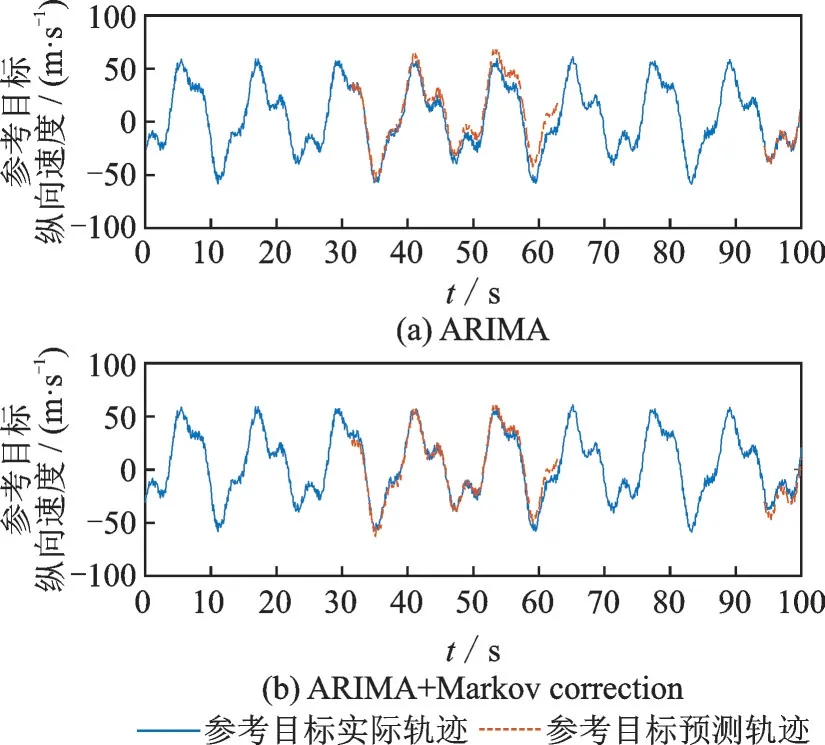
图2 纵向子系统ARIMA 预测及修正后结果对比Fig.2 Comparison of ARIMA prediction and correction results for longitudinal subsystem

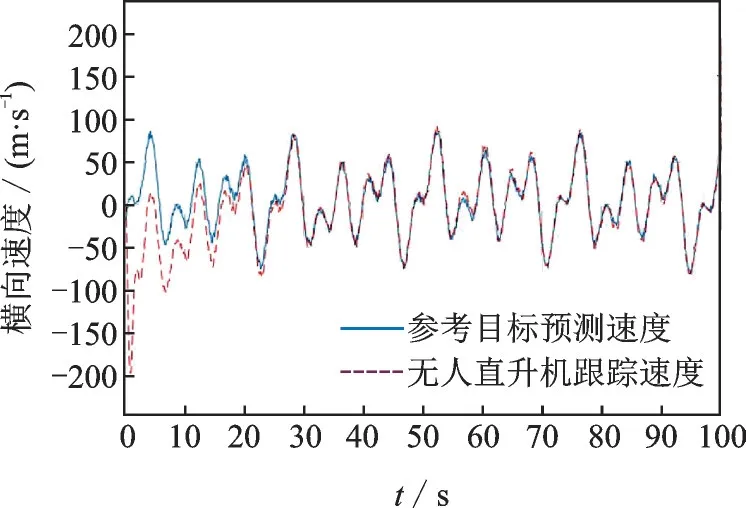
图3 横向子系统跟踪图Fig.3 Horizontal subsystem tracking diagram

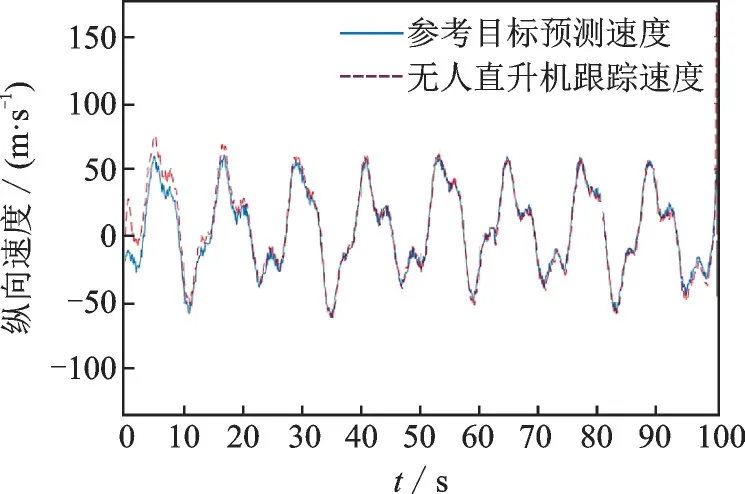
图4 纵向子系统跟踪图Fig.4 Longitudinal subsystem tracking diagram

由图3，4 可以看出，采用饱和函数设计控制器时，实际跟踪轨迹贴合参考运动轨迹且振幅较小。

5 结 论

本文针对受到随机扰动下UAH 空地协同跟踪控制过程中，遭遇地面参考信号短暂丢失时，基于跟踪目标轨迹数据的插值需要，提出以改进ARIMA 模型为基础的预测算法。该算法在ARI⁃MA 模型基础上融入马尔可夫状态迁移矩阵理论，能有效提高丢失信号预测模型估计精度，在短时预测上具有一定应用价值。采用自适应快速滑模控制，以减小外界扰动对跟踪性能影响，可提高跟踪速度和精度并抑制随机扰动对跟踪效果的影响。未来工作将所提出信号短暂丢失下预测模型和控制器设计，应用到实际UAH 系统以提升空地跟踪的控制性能。