多维探究,激发活力,提升素养

李 波

(四川省南充高级中学)

2022年高考数学试题落实了立德树人的根本任务,促进学生全面发展,试题以«普通高中数学课程标准(2017年版2020 年修订)»为指导,助力“双减”政策,稳中求新,全面体现数学学科特点,强化基础性、应用性,坚持素养导向、能力为重,突出关键能力,体现数学的应用价值,强化思想方法的渗透,考查学生的关键能力,发挥高校的选拔功能.如2022年全国乙卷理科第20题(文科第21题)考查了直线、椭圆、向量、同角三角函数的基本关系、图像变换、坐标系与参数方程、数列等知识,要求学生能够筛选出有效的题干信息,抓住问题本质,并利用有限的时间,选择较优的方法进行正确地运算,突出了对学生逻辑推理能力、数学运算能力的深入考查.本文对这道题进行多解探究与分析.

1 试题展示

(1)求E的方程;

图1

分析 第(1)问主要考查了椭圆的标准方程和分类讨论的数学思想.通过深入分析第(2)问,不难发现其主要考查了直线方程的几种形式、直线与椭圆的位置关系、三点共线在向量中的坐标运算、同角三角函数的基本运算(公式)、图像的平移和伸缩变换、利用直线与椭圆的极坐标和参数方程解决解析几何综合问题、等差数列等知识;考查了特殊到一般、换元、设而不求等基本方法,以及函数与方程、转化与化归等数学思想,入口易、口径宽、深入缓、出口难;突出对独立思考、逻辑推理、数学表达等关键能力的考查;重视概念,回归教材,对知识的考查由记忆走向理解,由结果走向过程,由双基走向核心素养,以体现数学的功能价值和学科特点.

2 解法赏析

综上,直线HN过定点(0,－2).

解法3 当直线MN的斜率为0 时,A,M,T,H,N五个点重合,直线HN过点(0,－2).

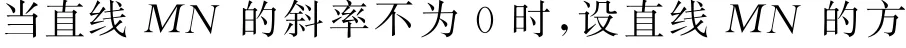
图2

当直线MN的斜率为0 时,A,M,N,P四 点 重合,直线HN过点(0,0).

综上,在原坐标系下,直线HN过定点(0,－2).

3 解后反思

3.1 通性通法的考查有活度

解题过程中不难发现,试题求解方法具有多样性,求解时常需要学生借助相关数学知识或方法建立数学模型,检测了学生数学知识的运用水平,尤其在解法优劣的评估方面,进而在落实高考数学对创新性考查的同时,考查学生对知识的灵活运用水平.

3.2 传承创新的延续有温度

证明 当直线MN的斜率不存在时,证明过程同

解法1,得出直线HN过点A(0,－b).

通过伸缩变换,将“椭圆”变成“圆”,上述结论仍然成立,体现了圆锥曲线的统一美和内在美.细心的读者不难发现,2022年高考全国乙卷理科第20题的题目中,直线PA,PB与椭圆E相切,由此,得出推广5和推广6.

推广5 已知圆O:x2＋y2＝r2(r＞0),点P(λ,μ)在圆外,过点P的直线l交圆O于M,N两点,直线PA,PB与圆O相切于点A,B,过点M分别作直线NA,NB的平行线交NB,NA于点F,E,交直线AB于T2,T1,则T1,T2分别是ME,MF的中点.

4 小结

多解探究既能促进教师专业快速成长,又可以提升学生的解题能力和对章节知识的整合水平,促使学生对试题进行深入探究、挖掘试题的深层背景、理解试题的命题立意、把控试题的命题趋势,提升复习的针对性和实效性.