减少圆锥曲线运算量的齐次化策略研究

王鹏程

(山西省阳泉市教学研究中心 045000)

在解圆锥曲线解答题时，基础的操作是直线和曲线联立，然后 “设而不求”用韦达定理计算.很多学生解题时，不管什么题目，都是一个解题套路，遇到常规题型还能得几分，如果运算量大一点，联立后就只能放弃了.有感于这一现状，笔者归纳总结了一些解题策略，以期望能帮助学生减少解圆锥曲线解答题时的运算量，以此为着眼点，本文着重对齐次化策略进行研究.

所谓齐次化策略是指在直线与曲线联立的过程中，构造关于斜率的二次方程，直接利用韦达定理得到斜率之和(积)的关系式，从而减少运算量的解题策略.齐次化策略在处理一些与斜率之和(积)有关的问题，能极大地减少运算量.

1 齐次化策略的基本原理

2 齐次化策略的简单应用

下面以具体题目来说明齐次化策略在圆锥曲线解答题中的应用：

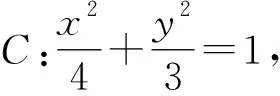
常规思路设直线MN的方程是

y=kx+m，Mx1,y1,Nx2,y2，

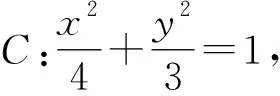
4k2+3x2+8kmx+4m2-12=0.

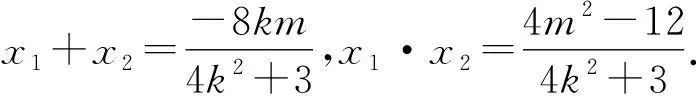
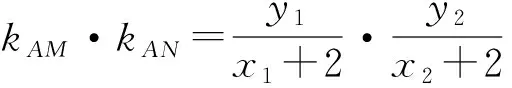
整理，得m=k或m=2k.

MN的方程是：y=kx+k或y=kx+2k，

由题意可知MN不过A-2,0.

所以直线MN过点-1,0.

首先可以利用截距式设直线方程为mx+ny=1，因为不过点A-2,0，所以可设为mx+2+ny=1.然后转化曲线的方程为

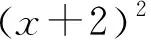
保留二次项不变，将一次项乘以直线方程的左边，得

4k2-12nk+3-12m=0.

则直线方程为x+2+ny=1，可知恒过点-1,0.

明显看出，采用齐次化的处理策略可以极大地减少运算量，其具体步骤可以概括为：先根据斜率的形式巧设直线的方程，然后对曲线的方程作变形，联立将所有项都凑成二次项(齐次化)，再同除一个代数式构造出关于斜率的二次方程，最后利用韦达定理求解即可.

再以一个题目为例，来进一步地说明齐次化的优势.

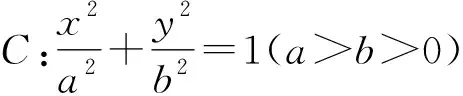
(1)求椭圆C的方程；

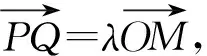
(2)常规解法如下：

因为∠PMQ的平分线垂直于AO，则直线PM,QM关于x=2对称.

所以kPM+kQM=0.

设PQ:y=kx+m,Px1,y1,Qx2,y2

将直线PQ的方程代入x2+4y2=8,得

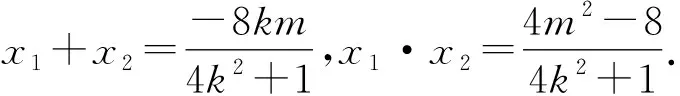
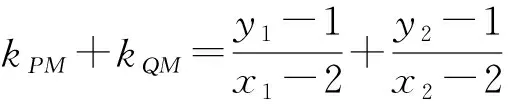
整理,得

2kx1x2+m-1-2kx1+x2-4m-1=0.

代入，化简,得2k-12k-1+m=0.

因为PQ不经过2,1, 所以2k+m≠1.

所以2k-1=0.

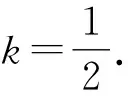
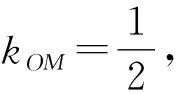
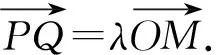
同样，常规解法思路简单，但是在得出2k-12k-1+m=0这一步时大部分学生很难完成， 采用齐次化策略求解，具体步骤如下：

解析因为∠PMQ的平分线垂直于AO，则直线PM,QM关于x=2对称.

所以kPM+kQM=0.

设Px1,y1,Qx2,y2，则

根据题意，PQ直线不经过点M,设其方程为mx-2+ny-1=1.

将椭圆C的方程整理,得

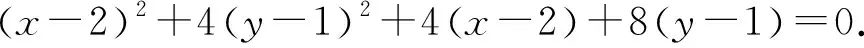
将直线的方程代入，得

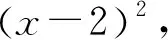
8n+4k2+8m+4nk+4m+1=0.

解得n=-2m.

所以PQ直线方程为mx-2-2my-1=1.

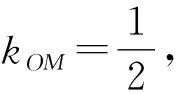
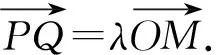
3 齐次化策略在高考中的应用

在最近几年的高考题中，有很多考题可以采用齐次化策略求解，如2017年新课标Ⅰ卷(理)，2018年新课标Ⅰ卷(理)， 2020年新高考(山东)卷，2020年新课标Ⅰ卷(理)等.接下来以2020年新课标Ⅰ卷(理)21题为例，进一步来说明齐次化策略在应试时的优势.

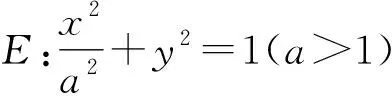
(1)求E的方程；

(2)证明：直线CD过定点.

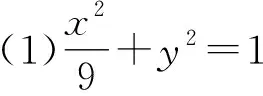
(2)常规思路如下：

设P6,y0，则直线AP的方程为

联立直线AP的方程与椭圆方程得

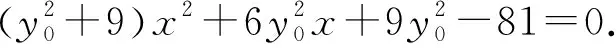
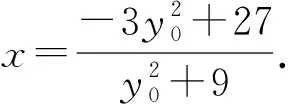
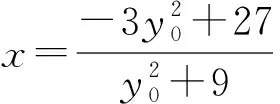
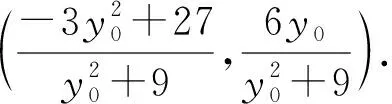
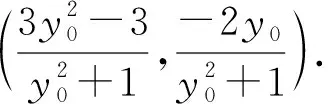
所以直线CD的方程为

整理,得

整理,得

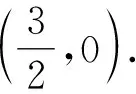
可以明显感觉到上述过程的复杂性，利用齐次化策略求解，其步骤如下：

由题意可知A-3,0，A3,0，设P6,y0，则

所以kPB=3kPA.即kDB=3kCA.

设Cx1,y1，Dx2,y2,则

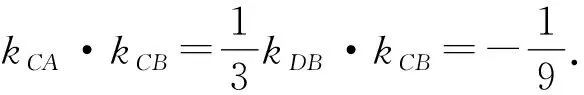
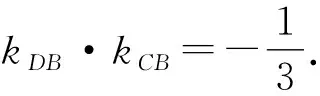
设CD的方程为mx-3+ny=1，

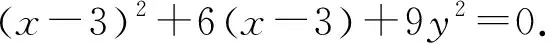
代入直线的方程，得

9k2+6nk+6m+1=0.

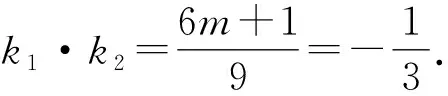
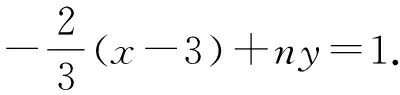
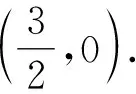
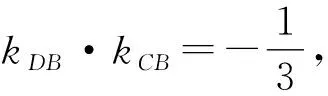
4 对齐次化策略的思考

本文齐次化的解题核心是依据斜率的形式对圆锥曲线方程变形，构造出齐次式，从而得到斜率的二次方程，这一步骤也可以通过平移圆锥曲线来实现.由于教材中圆锥曲线的方程都是标准方程，所以在实际教学中感觉学生对平移圆锥曲线不好理解，故没有按照这个方法解题，读者可以根据自己的理解择优选择.

齐次化策略不是一个普适性的解题方法，只适用于与斜率之和(积)有关的一类问题，但是不能因此就舍弃这一好的方法，也有很多只能解决一类问题的巧妙方法，如 “点差法”等，这些技巧也值得学生掌握.

教学中发现很多学生感觉对曲线变形的步骤似乎在“化简为繁”，因而不愿意接受齐次化策略.应该引导学生认识到“化简为繁”的目的是为了后续的计算变得简单，这一变化看起来复杂，但是经过简单的练习很快就能掌握.客观地说，齐次化策略也有一些不足之处，比如在需要计算判别式时运算量反而会增加，因此在解题时需要根据具体问题来进行选择.