活用定义 巧解圆锥曲线考题
——以2022届八省联考第5题为例
贺凤梅
(新疆维吾尔自治区伊犁巩留县高级中学 835400)
在近几年的高考试题中,抛物线以选择题、解答题的形式出现.2016年全国Ⅰ卷理科第10题、2018年全国Ⅱ卷理科第19题、2021年全国乙卷理科第21题均考查了抛物线.2022届八省联考题以选择题的形式进行了考查,彰显了抛物线定义应用的普遍性,从试题设置来看,也突出了解题的技巧性和灵活性.如果只是按部就班地解此题,很可能在考场上耗费大量时间还未成功,从而对考生的心理造成消极的暗示,影响其他试题的解答.下面以2022届八省联考题为例,期待通过思路的分析及解法的对比,厘清问题的本质.
1 问题的提出
题目(2022届八省联考第5题)如图1,抛物线C:y2=4x的焦点为F,直线l与C交于A,B两点,l与y轴交于点E,已知|AF|=7,|BF|=3,记△AEF的面积为S1,△BEF的面积为S2,则( ).
A.S1=2S2B.2S1=3S2
C.S1=3S2D.3S1=4S2
2 解法探究
解法1(以两个三角形的底和高为研究对象)
设AB与x轴的交点为P,以PF为两个三角形的公共底边,高由对应两点纵坐标之差的绝对值确定,设A(x1,y1),B(x2,y2),结合图1有y1>0,y2<0.
由抛物线的定义,得|AF|=x1+1=7,
解得x1=6.
由|BF|=x2+1=3,解得x2=2.
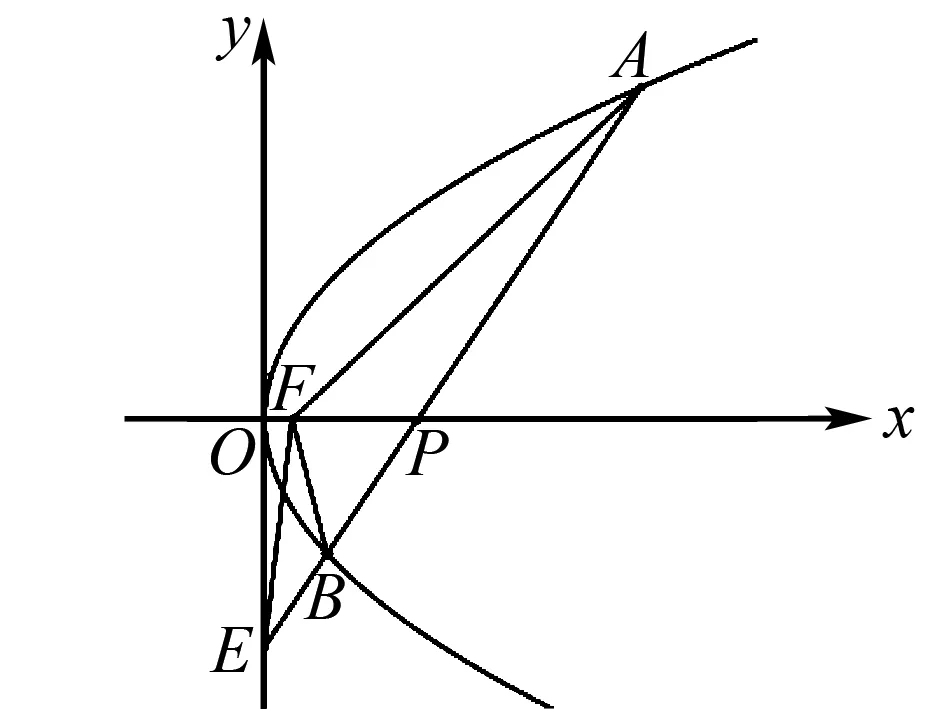
图1

所以直线AB的方程为


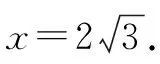


S△BEF=S△EFP-S△BFP

故选C.
评析此种解法思路自然,没有变形技巧和思维难度,需要什么求什么. 但从解题过程来看,不亚于一道大题的计算量. 如何破解此题,实现小题小做,小题巧做呢?重新审视此题,既然题设中与焦点弦有关,我们要充分利用抛物线的定义和性质,还有两三角形的面积如何表示,能实现面积的比与已知条件中线段的长度建立相对直接的关系,题目就简单很多.
解法2 (利用抛物线的定义,借助平面几何知识解答)如图2,作AA1⊥y轴于点A1,作BB1⊥y轴于点B1,所以AA1∥BB1.
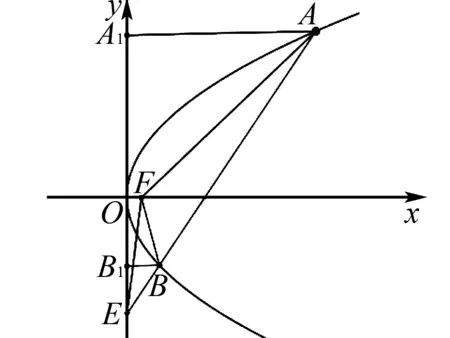
图2
由抛物线的定义,得


设点F到AB的距离为d,
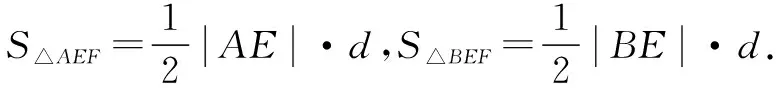
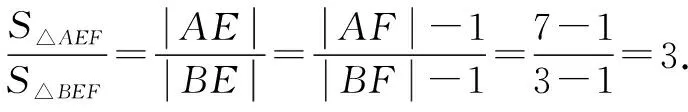
故选C.
评注此法利用抛物线的定义及几何位置关系进行等价转化,将化归与转化、数形结合的思想和方法体现得淋漓尽致,很好地领悟了命题者的意图.
3 举一反三
如果题设中出现了抛物线的焦点、焦半径、抛物线上的点及准线时,一般应考虑利用抛物线的定义解题,而对抛物线有关问题的求解,若能巧妙利用定义转化,则常能化繁为简,优化解题思路,节省解题时间,提高解题效率,拓展思维能力.下面分类举例.
3.1 比值问题

解析设A(x1,y1),B(x2,y2),不妨设y1>0,y2<0,作AE垂直于准线于点E,作BD垂直于准线于点D,如图3.由抛物线的定义知|BF|=x2+1=5.

图3
所以x2=4.由题设可求得y2=-4.
所以B(4,-4).则AB的方程为y=4x-20.
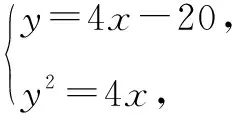
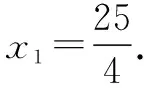


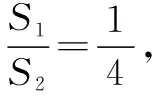

2x2-(p+8)x+8=0.
设A(x1,y1),B(x2,y2),由根与系数的关系知
①

②
联立①②解得x1=4,x2=1.
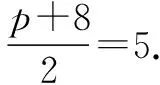
3.2 长度问题
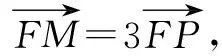

3.3 最值问题
例4设抛物线y2=2x的焦点为F,点P是抛物线上的动点,点A(3,2),当|PA|+|PF|取最小值时,点P的坐标为____.
评析与抛物线有关的最值问题,优先考虑抛物线的定义,当然抛物线的定义在应用上有很大的灵活性,这对学生的思维能力和转化能力提出了更高的要求.正所谓“看到焦点作准线,看到准线连焦点”.(参考答案:P(2,2).)
3.4 参数问题
例5过抛物线y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为____.
评析本题是山西大学附中2019届的一道适应性检测压轴题,有一定的难度和灵活性,但只要利用定义进行等价转化,还是可以突破的.(参考答案:y2=3x)
抛物线的定义揭示了抛物线的内涵与外延,也反映出它的本质,在解题教学中,我们倡导要回归课本,回归定义.美国著名数学教育家波利亚在《怎样解题》一书中说到“回到定义上去是一种重要的思维活动”.因此,用好定义解题很重要,它不仅可以使问题得到简化,还能提高学习效率,增强学生学习的兴趣和自信心.

