一类高考试题隐藏的一个秘密

傅建民

(陕西省咸阳市渭城中学 712000)

首先介绍射影几何当中的几个结论：

定理1设点P关于常态二次曲线Φ的极线为l，过点P的直线l′与常态二次曲线Φ交于M，N两点，若直线l′与极线l交于点Q(如图1)，则点列M,N,P,Q为调和点列.

图1

定理2如果线束S的四直线a,b,c,d被一条直线s所截，交点顺次为A,B,C,D(如图2)，则它们的交比相等，即(AB,CD)=(ab,cd).

图2

因此调和点列对应的线束为调和线束.

定理3如果调和线束S的四直线a,b,c,d被一条平行于直线d的直线s所截，交点顺次为A,B,C(如图3)，则C为线段AB的中点.

图3

(1)求E的方程；

图4 图5

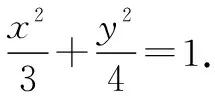
连接AP,AM，如图5，由定理1，2可知，线束AM,AN,AB,AP为调和线束.

又因为MH∥AP，由定理3可知，T为HM的中点，即直线HN过定点A.

下面我们从解析几何的角度来分析.

所以3y1=x1+x3-6.

所以x3=3y1-x1+6.

如果直线MN∥y轴，

因为点T在直线AB上，

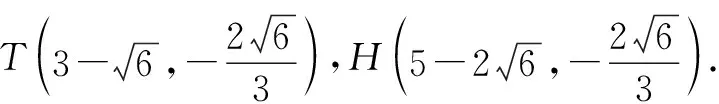
可以验证N,H,A三点共线.

如果直线MN的斜率存在，设直线MN方程为y+2=k(x-1),所以y=kx-(k+2).

整理,得

(4+3k2)x2-6k(k+2)x+3k(k+4)=0.

其中Δ=[6k(k+2)]2-4(4+3k2)[3k(k+4)]>0,

解得k>2或k<0.

此时，N,H,A三点共线于y轴.

如果x2≠0，那么x3≠0.

下面验证直线HN过定点A:

即(3k-1)kx1x2-k(3k-1)x1-3k2x2+3k2=kx1x2-kx2.

即(3k-2)kx1x2-k(3k-1)(x1+x2)+3k2=0.

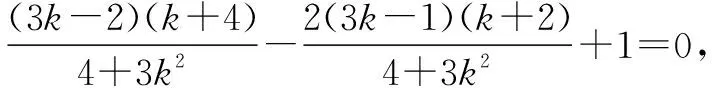
即直线HN过定点A.

(1)求椭圆E的方程；

(2)如图6，过点P(-2, 1)作斜率为k的直线与椭圆E交于不同的两点B,C，直线AB,AC分别与x轴交于点M,N，当|MN|=2时，求k的值.

图6 图7

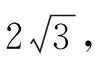
(2)记椭圆E的左顶点为D，如图7，连接AP,AD，点P与直线AD恰好是一对极点极线，因此线束AC,AB,AD,AP为调和线束.

又因为AP平行x轴，所以点D为线段MN的中点.下面我们用解析法来求解该问题(2)

即x=3y-3.

即13y2-18y+5=0.

即(13y-5)(y-1)=0.

所以直线PB的斜率

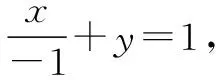
即x=y-1.

代入椭圆方程,得

即5y2-2y-3=0.

即(5y+3)(y-1)=0.

所以直线PC的斜率

所以P,B，C三点共线.

故所求的直线的斜率k=-4.

图8 图9

(1)求抛物线C的方程，并求其焦点坐标和准线方程；

(2)求证：A为线段BM的中点.

解析(1)因为抛物线y2=2px经过点P(1, 1)，所以1=2p.

设OP与l的交点为G，则M,N,G,D为调和点列，所以OM,ON,OG,OD为调和线束.即OM,OB,OA,OD为调和线束，而直线MA∥OD，所以A为线段BM的中点.

通过上面例题的解析，我们洞悉了出题人的构题思路.对于解题者来说，通过射影几何发现了问题当中的玄机，从而将探索性问题变成了验证性问题，大大减少了计算量.