强化“几何”特征 重视“结合”意识
——例谈解析几何中强化“几何”特征和综合解题意识培养
巨小鹏
(陕西省汉中市龙岗学校 723102)
解析几何问题首先要搞明白试题要解决的是什么样的几何问题,其次要弄清楚解决这个几何问题是否需要转化至代数问题解决,如果需要,是否需要建立坐标系,如果可以借助几何特征解题,那么借助哪些几何特征或几何工具,或者看是否需要数形结合,代数和几何相互借力,将复杂问题等价转化至较为简单的问题(有时候这个转化过程不是很直观,需要把几何问题转化为另一个等价的几何问题后再进行代数化),利用已知的题设条件,分析这些条件之间的联系,研究并解决转化之后的问题,从而解决解析几何问题.
1 利用“几何”特征,培养直观想象能力
例1(2019年全国Ⅰ卷·10)如图1,已知椭圆C的焦点为F1(-1,0),F2(1,0),过点F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( ).
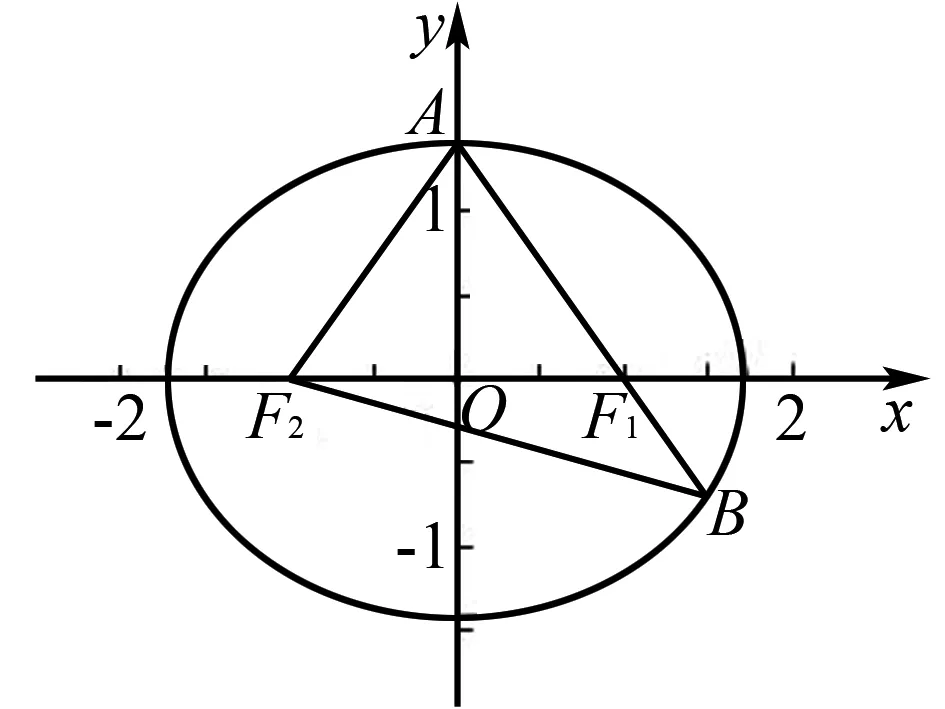
图1
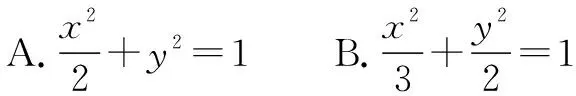
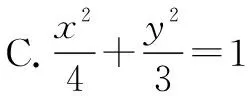
解法1(同角视角法) 由已知设|F2B|=m,则|AF2|=2m,|BF1|=|AB|=3m.
根据椭圆的定义知|BF1|+|BF2|=4m.
则|AF1|=2a-|AF2|=2m.
在△AF1B中,由余弦定理得
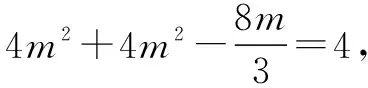
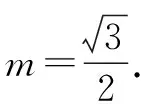
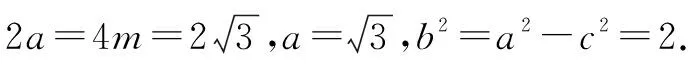

解法2(邻补角法)由解法1可知
|BF1|=|AB|=3m,|AF1|=2m.
则在△AF1F2和△BF1F2中,由余弦定理,得
又由图可知∠AF2F1+∠BF2F1=π.
则cos∠AF2F1+cos∠BF2F1=0.
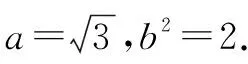

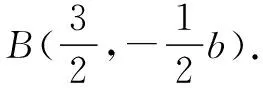
代入椭圆方程得a2=3,b2=a2-c2=2.
故选B.
评注本题考查椭圆定义及其简单性质,考查数形结合思想、转化与化归的能力,特别是利用几何特征解题,形象直观,解法1把一个角放在不同的三角形中研究,利用余弦定理建立方程解决问题,解法2利用邻补角的余弦值互为相反数解决问题,解法3借助辅助线利用已知线段比建立相似比解决问题,很好地考查了直观想象能力和逻辑推理能力.
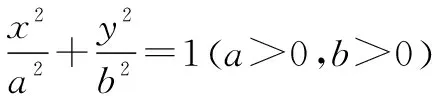
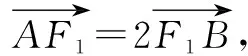
根据椭圆定义可知
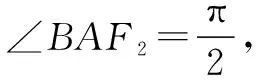
即(3m)2+(2a-2m)2=(2a-m)2,
解得a=3m.
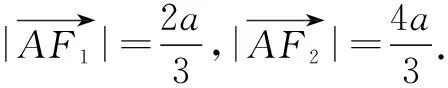
在△AF1F2中,直线AB的斜率为
因为a=3m,在Rt△AF1F2中,
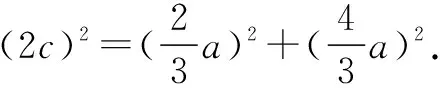
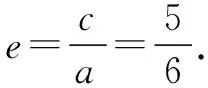
评注利用平面几何解题更加直观,本题利用图形的“几何”特征,在几何图形中寻找等量关系,结合椭圆定义和解三角形计算,从而求出直线的斜率和椭圆的离心率,考查推理分析、运算和图形分析能力.
2 代数几何相结合,彼此借力内化思维品质
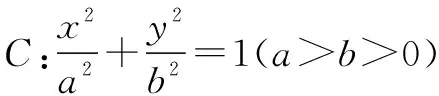
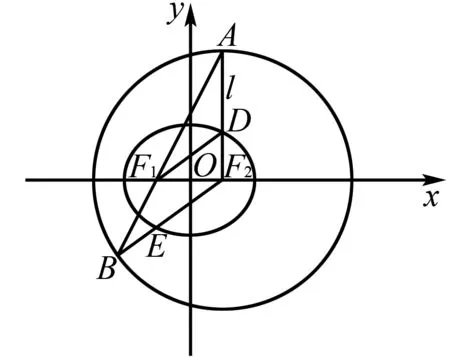
图2
(1)求椭圆C的标准方程;
(2)求点E的坐标.
解析(1)可知F1(-1,0),F2(1,0),所以F1F2=2,c=1.
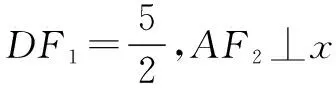
因此2a=DF1+DF2=4.
从而a=2.解得b2=3.
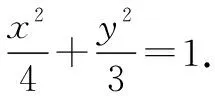
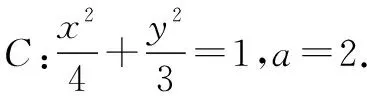
因为AF2⊥x轴,将x=1代入圆F2的方程(x-1)2+y2=16,得y=±4.
因为点A在x轴上方,所以A(1,4).
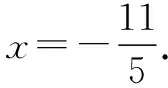

又因为E是线段BF2与椭圆的交点,
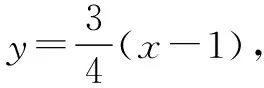
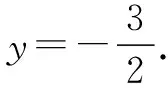
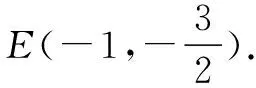
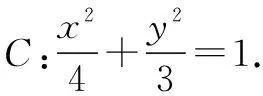
图3
从而∠BF1E=∠B.
因为F2A=F2B,所以∠A=∠B.
所以∠A=∠BF1E.
从而EF1∥F2A.
因为AF2⊥x轴,所以EF1⊥x轴.
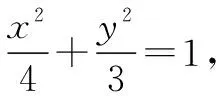
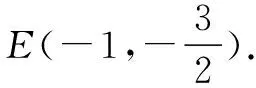
评注解法1明显比解法2计算复杂,利用平面几何知识,从“几何”特征入手研究题目中的几何关系是必要的,在这个过程中,要经历文字信息、图像特点和符号语言之间的多重转换.
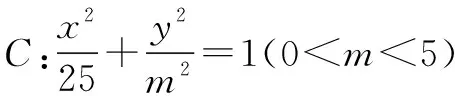
(1)求C的方程;
(2)若点P在C上,点Q在直线x=6上,且|BP|=|BQ|,BP⊥BQ,求△APQ的面积.
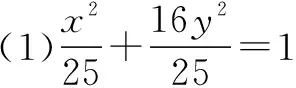
(2)解法1 (通性通法)设P,Q在x轴上方,过点P作x轴垂线,垂足为点M,设直线x=6与x轴交点为N,根据题意画出图形,如图4.
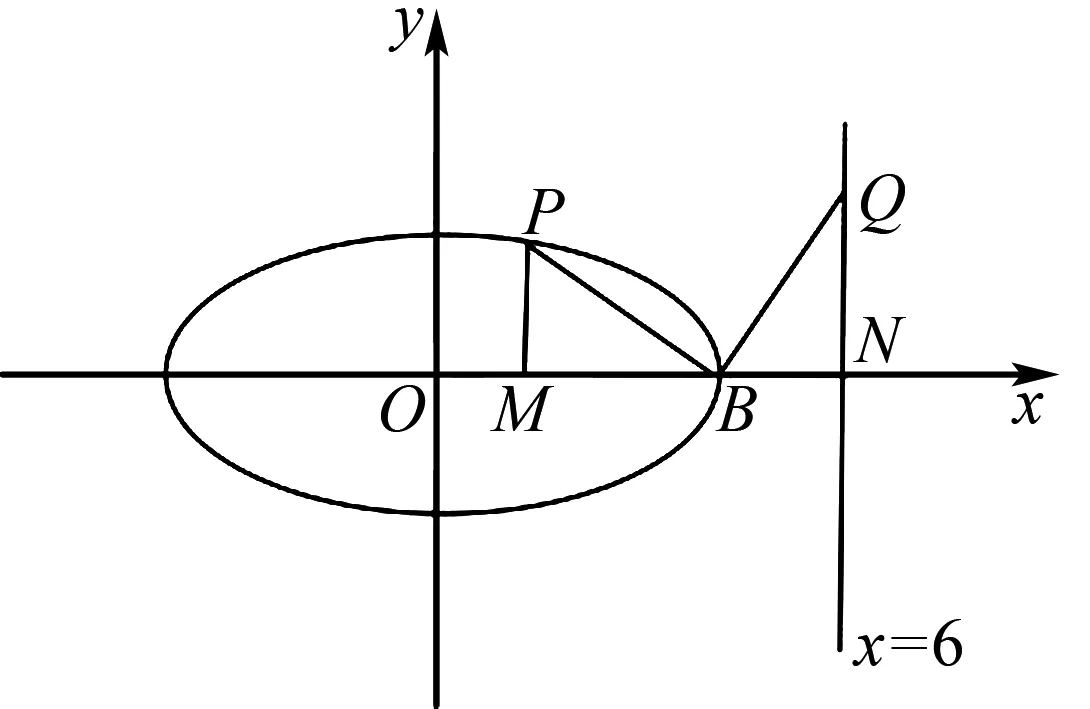
图4
因为|BP|=|BQ|,BP⊥BQ, ∠PMB=∠QNB=90°,∠PBM+∠QBN=90°, ∠BQN+∠QBN=90°,所以∠PBM=∠BQN.
根据三角形全等可得△PMB≌△BNQ.

所以|PM|=|BN|=6-5=1.
设点P为(xP,yP),可得点P纵坐标为yP=1.

解得xP=3或xP=-3.
所以点P为(3,1)或(-3,1).
①当点P为(3,1)时,|MB|=5-3=2.
因为△PMB≌△BNQ,
所以|MB|=|NQ|=2.
可得点Q为(6,2).
如图5,因为A(-5,0),Q(6,2),可求得直线AQ的直线方程为2x-11y+10=0.
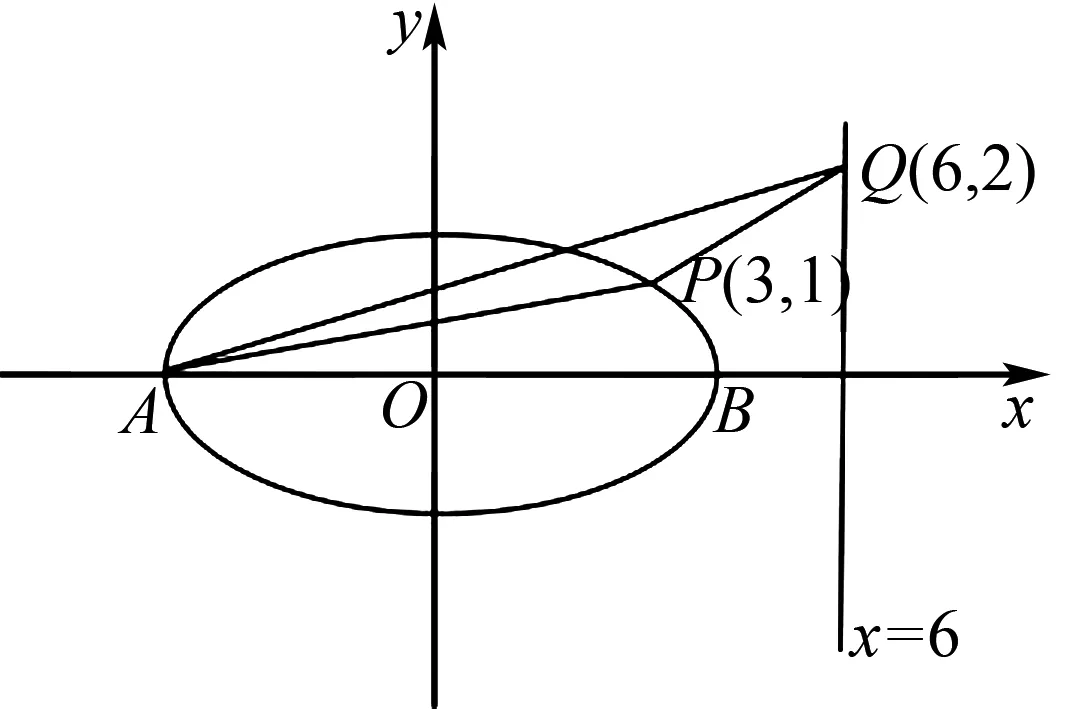
图5
可得P到直线AQ的距离为
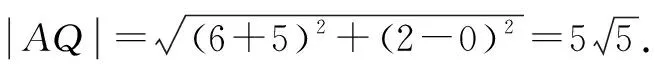
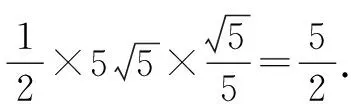
②当点P为(-3,1)时,|MB|=5+3=8.
因为△PMB≌△BNQ,所以|MB|=|NQ|=8.
所以点Q为(6,8)
如图6,,因为A(-5,0),Q(6,8),直线AQ的方程为8x-11y+40=0,可得点P到直线AQ的距离为
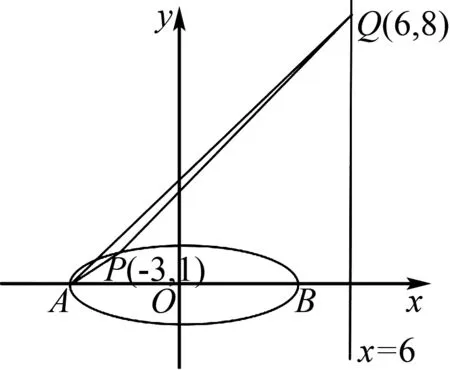
图6

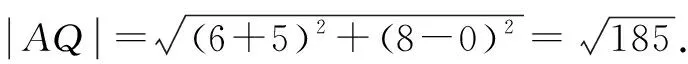
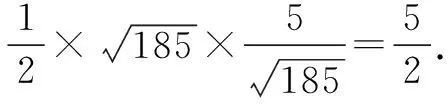
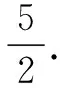
解法2(分割面积法)由对称性,不妨设点P,Q在x轴上方,过点P作PE⊥x轴,垂足为点E.设D(6,0),由题知,△PEB≌△BDQ.
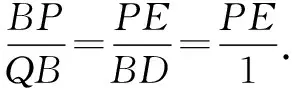
所以PE=1.所以xp=±3.

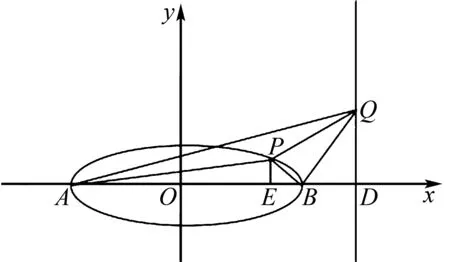
图7

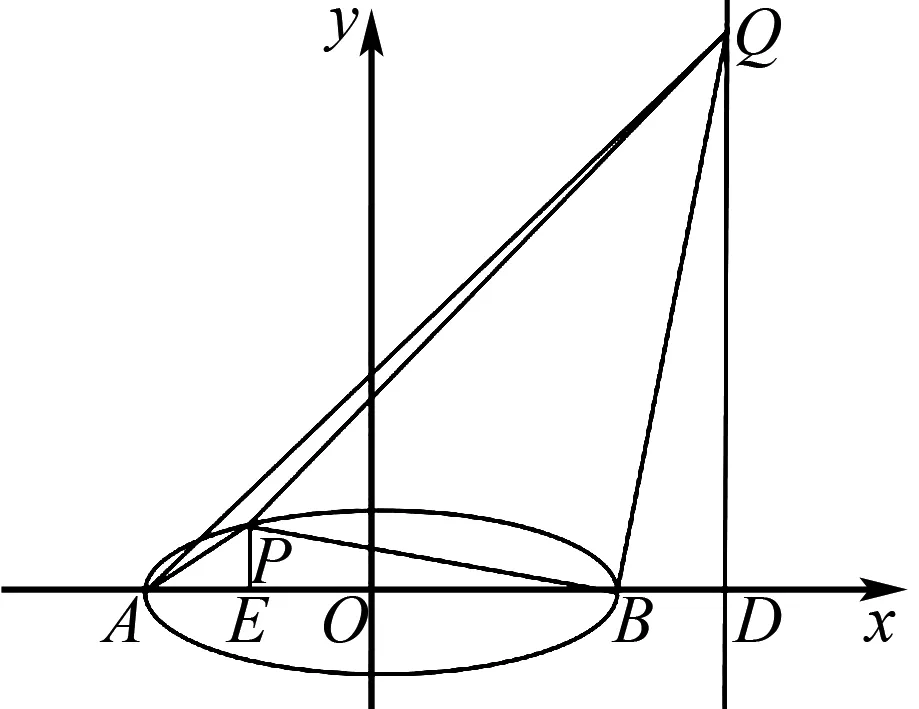
图8
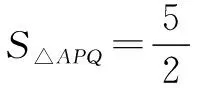
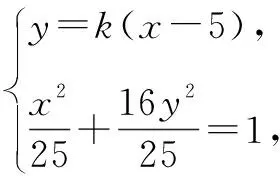
(1+16k2)x2-160k2x+16×25k2-25=0.
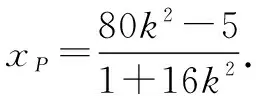
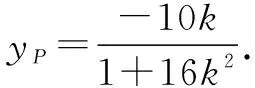
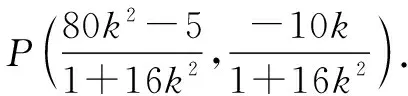
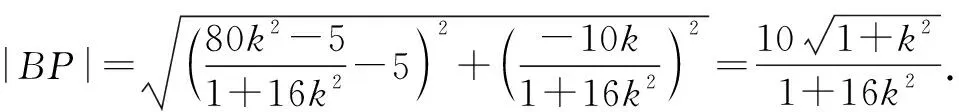
因为BP⊥BQ,则直线BQ的方程为
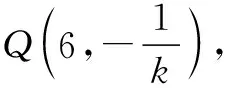
因为|BP|=|BQ|,
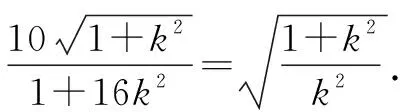
即256k4-68k2+1=0.
即(64k2-1)(4k2-1)=0.
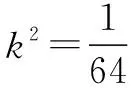
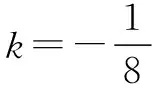
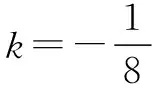
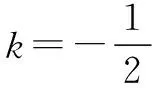
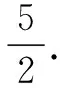
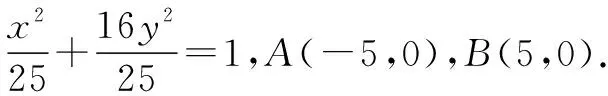
不妨设P(x0,y0)在x轴上方.
设直线AP:y=k(x+5)(k>0),
因为|BP|=|BQ|,BP⊥BQ,
所以y0=|BN|=1,yQ=|BM|=5-x0.
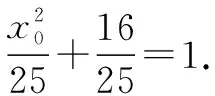
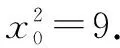
由点P在直线AP上得1=k(x0+5).
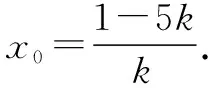
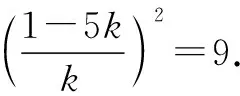
化简得16k2=10k-1.
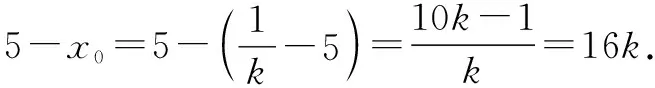
即Q(6,16k).
所以点Q到直线AP的距离

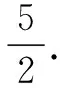
解法5(面积坐标法) 由对称性,不妨设点P,Q在x轴上方,过点P作PC⊥x轴,垂足为点C,设D(6,0),由题知△PCB≌△BDQ.
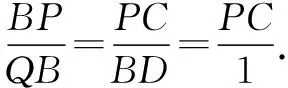
所以PC=1.
所以xp=±3.
当P(3,1),A(-5,0),Q(6,2),则
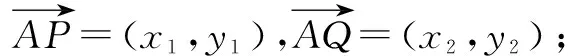
当P(-3,1),A(-5,0),Q(6,8),同理,
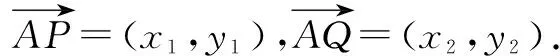
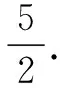
评注对于第(2)问解决视角很多,解法1根据平面几何知识,利用“几何”特征可求得点P的坐标,从而得到点Q的坐标以及直线AQ的方程,再根据距离公式即可求出三角形的面积,也是大多数人能想到的方法,是为通性通法;解法2同解法1,最后利用图形面积分割法求△APQ的面积,优化处理后计算有所简化;解法2利用代数法通过设直线BP的方程y=k(x-5)与椭圆的方程联立,求出点P的坐标,再利用等量关系求出k的值,从而得出点Q的坐标以及直线AQ的方程,最后根据距离公式即可求出三角形的面积,方法容易想到但计算量比较大;解法4与解法3类似,设直线AP的方程y=k(x+5)(k>0),通过平面知识求出点P的坐标,表示出点Q,再根据距离公式即可求出三角形的面积,计算量也不小;解法5同解法1最后利用了三角形面积坐标法,需要很强的逻辑推理能力利用向量法推出公式,当然北师大版必修五第二章第一节正弦定理例3介绍过公式的推导过程,所以注重课本例题和习题显得尤为重要.
解析几何问题中几何是思考的起点和终点,也是问题的缘起和归宿,代数化和“几何”特征是解决几何问题的工具.加深几何特征和曲线与方程有关概念的理解,以提升“猜想证明、化归转化、直观想象、数学运算、严谨逻辑推理和探索实践应用”等关键能力为目标,内化数学核心素养.

