改进DTW下界函数的距离度量方法研究

王 超，龙英文，殷炜宏，黄 勃

上海工程技术大学 电子电气工程学院，上海 201620

时间序列数据通常出现在许多应用领域，例如医学的脑电波和心电数据[1]、气象天文数据[2]、股票证券交易数据[3]和工业用电数据[4]等。尽管如今的数据库随着相关应用的增加而持续增长，但一个普遍的需求是去找到时间序列之间的相似性[5]。作为一种度量两个序列相似程度的方法，时间序列相似性度量是时间序列异常检测、聚类、分类、相关规则提取和模式识别等工作的重要子进程[6]。因此，寻找一种合适的度量方法将会对后续的时间序列挖掘任务的效率和性能产生深远影响[7]。

在相似性度量方法中，动态时间弯曲（dynamic time warping，DTW）定义了序列之间最优对齐匹配关系，并支持两个不等长时间序列之间的相似性度量和时间轴的伸缩与弯曲。不同于欧氏距离（ED）“点对点”的线性映射匹配策略，且要求两条时间序列的长度必须相等。DTW允许将向量分量与从完全对应的位置“漂移”进行比较，即非线性映射[8]，用于寻求两个序列间的最优对齐方式，是一种常规的距离度量方法。

DTW的距离度量效果影响着挖掘工作结果，许多研究者都将动态时间弯曲的改进工作作为主要研究任务。其改进任务主要分为两类[9]：（1）设计出满足动态时间弯曲下界要求的下界函数；（2）针对动态时间弯曲算法过程的改进。

相似性度量工作较多用到下界函数，原始DTW距离度量的时间复杂度高，因此研究者提出利用DTW的下界，过滤掉不满足相似性要求的序列，有效提高了时间序列相似性搜索的性能。为保证准确高效的相似性度量，DTW下界距离应满足以下三个条件[10-11]：

（1）有效性：下界距离度量的时间计算成本应保持在低位值；

（2）紧凑性：下界距离的度量结果应尽可能接近DTW距离，即保证候选集在规定量级的情况下，从而减少后期再处理的工作量；

（3）正确性：经过下界距离函数筛选得到候选序列，必须包含所有满足条件的序列，即不准出现误报、漏报现象。

Yi[12]、Kim[13]、Keogh[14]等人分别提出支持DTW距离度量的边界距离函数。LB_Yi是由Yi等人提出的首个针对DTW的低边界函数。为了构建DTW下界距离，该函数以一条时间序列作为基本度量序列，将另一条序列中小于基本度量序列的最小值点集和大于该基本序列最大值的点集作为特征，从而完成构建。Kim等人提出了LB_Kim函数，它比LB_Yi更接近真实DTW下界距离，其核心思想是：选出两个序列的第一个序列特征值、最后一个序列特征值、最大值及最小值这4个特征值，然后计算对应特征值的绝对差值，以最值作为边界距离，构建DTW下界距离函数。Keogh等人利用全局时间弯曲约束，构造约束动态弯曲路径的上下边界，并提出了下界距离函数LB_Keogh，它比LB_Kim和LB_Yi更接近真实DTW下界距离。

Jeong、Sakurai分别针对算法过程进行改进。文献[15]Jeong等人为了优化动态时间弯曲度量效果，提出了WDTW方法，通过赋予在距离矩阵中时间序列数据点的相位差高的元素更高的惩罚权重，避免了时间序列过度弯曲和不合理匹配的问题。而文献[16]Sakurai等人利用early stopping，即提前终止思想，在计算累计矩阵时，当出现比当前累积值大的单元格时，终止该单元格后的行（或列）之后的所有单元格的计算，从对角线的新单元格开始计算，减少计算成本。

文献[17]Górecki等人将DTW和时间序列的一阶导数相融合，即根据时间序列的一般形状特征，提出一种新的距离度量方式DDDTW，该距离度量经过实验证明取得了不错的效果。文献[18]Górecki等人对上述方法做出进一步改进，在上述研究成果的前提下结合时间序列特征的二阶导数，又进而提出一种新的距离度量2DDDTW。该相似性度量方法与文献[17]相比，分类效果有了更进一步。

文献[19]晏臻等人提出一种改进的基于下界函数的DTW相似性搜索方法——NLB-FDTW。该方法从下界函数入手，首先经过序列标准化后，再采用LB_Kim对序列进行首次下界函数过滤，筛选掉那些不相似的序列，然后再采用所提出的LB_Lweng方法进行二次过滤，即采用LB_Lweng下界距离度量序列之间的相似距离，并初始化阈值ε，若LB_Lweng距离大于ε，则将该候选序列剔除相似候选序列集合，否则就将该序列加入到相似候选集中。最后，再从相似候选集中找出k个最为相似的序列进行相似匹配。

但到目前为止，已有的基于下界函数的DTW距离度量方法仍缺少良好的均衡性，即上述的现存研究方法虽然保证了算法的准确性却难以提高算法的时间效率，而有些方法降低了计算成本，却无法保证度量的准确性与稳定性。

针对上述问题，本文综合考虑了度量的准确性和时间效率，采用提前终止思想，找到一种基于DTW的下界距离函数。即在下界距离函数的基础上，提出一种基于early stopping的DTW下界距离函数方法。进而，通过实验对所提方法进行计算效率、紧凑性和分类准确性分析。

1 相关定义

定义1（时间序列）时间序列是一组由连续时间变量和对应的特征值组成的有序集合[20]，从时间序列的角度来看，每个数据单元可以被抽象成一个二元组(t,v)，其中t为时间变量，v为特征值变量。定义时间序列X={x1=(t1,v1),x2=(t2,v2),…,xn=(tn,vn)}，并满足ti＜ti+1(i=1,2,…,n-1)，并且保证时间间隔固定，一般取Δt=ti+1-ti=1。此时，将时间序列简记为：

定义2（DTW距离）设时间序列S={s1,s2,…,sn}，Q={q1,q2,…,qm}，DTW距离实际上就是找到序列S与Q上每个点之间的对齐匹配关系[21]，如图1（a）所示，这种匹配关系可能有很多种，每一种匹配关系可以用一条弯曲路径表示，如图1（b）所示。也就是说，序列间的匹配关系与弯曲路径是一一对应的关系。

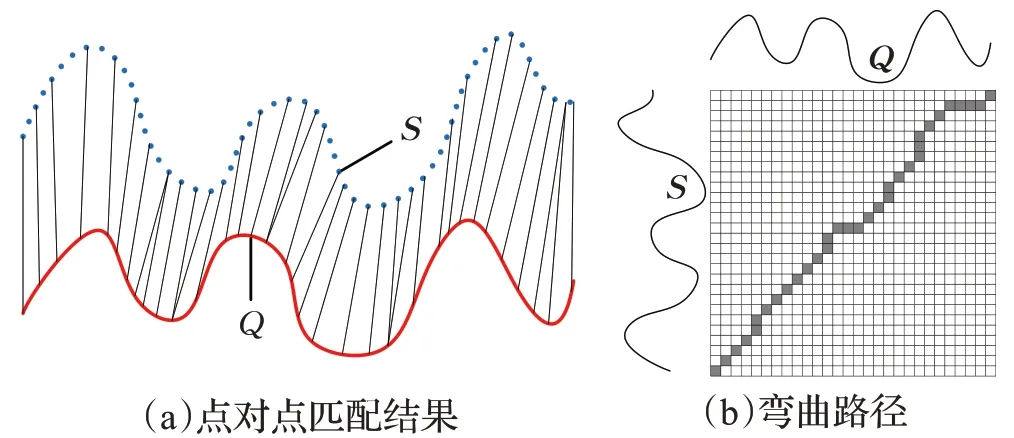
图1 弯曲路径与点对点匹配结果Fig.1 Matching result of warping path and point-to-point

为计算S和Q的DTW距离，需要构造一个m×n的矩阵，其中：

为向量点si和qj间的基距离，其中i=1,2,…,n，j=1,2,…,m，可根据不同情况选择不同距离度量。本文将采用欧氏距离作为基距离，即l=2。为计算DTW(S,Q)，需找到一条最优的弯曲路径，其中弯曲路径W中的第k个元素定义为wk=()i,j k，由此可得：

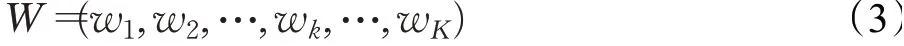
弯曲路径长度满足max(m,n)≤K≤m+n-1。

弯曲路径W必须满足3个特性[22]：

（1）边界性：路径起始于(s1,q1)、终止于(sm,qm)，它表示两个序列的起始点和终止点的对应匹配；

（2）连续性：弯曲路径上的任意两个相邻元素wk(i,j),wk-1(i",j")需满足0≤|i-i"|≤1,0≤|j-j"|≤1；

（3）单调性：若(i,j)和(i",j")为路径上前后相邻的两个点，则要满足i-i"≥0，j-j"≥0。

在众多弯曲路径中找到唯一最优的路径，使得累积距离达到最小：

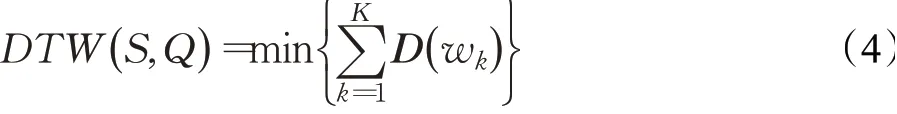
为求式（4），则需要利用动态规划方法构造一个代价矩阵γ。

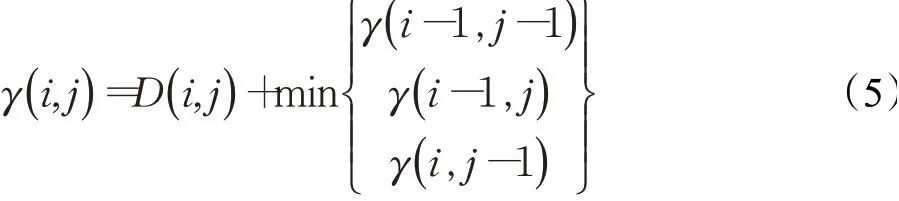
其中，i=1,2,…,n，j=1,2,…,m，γ(0,0)=∞，γ(i,0)=γ(0,j)=∞。那么，γ(i,j)可以看成是当前元素的基距离值与3个元素累积距离值的最小值之和。最终得到的γ(n,m)就是DTW距离度量S和Q的最小累积代价，即DTW(S,Q)=γ(n,m)。以此，便可找到最优的弯曲路径。

定义3（下界函数）对于时间序列的相似性度量[23]，若单纯使用DTW度量，时间复杂度会很高。出于计算成本的角度考虑，可以根据设定条件利用快速下界算法筛选出较为匹配的候选序列，之后再进行下一步的精确度量，从而加快时间序列度量精度。因此，任意两条时间序列距离值的特点是，一定小于等于这两者之间的DTW距离，即LB(S,Q)≤DTW(S,Q)，下一章在改进DTW距离的同时也将证明该下界函数定理的合理性。

2 基于DTW下界函数的提前终止算法

2.1 弯曲路径的全局约束

为了提高相似性度量效率，采用全局约束来提高度量算法的效率成为了关键，也就是规定了某个待查询序列的某个点与候选序列的约束范围内的几个点进行动态匹配。设时间序列S、Q的弯曲路径上的元素为wk=(i,j)k，那么弯曲路径的全局约束可以理解为对wk中k的限制，即其边界为j-r≤i≤j+r。r表示了序列上某点的弯曲路径局限性。对带状约束Sakeo-Chiba来说，r的取值与i不相关联，如图2（a）；而对于平行四边形约束Itakura-Parallelogram来说，r是关于i的函数，如图2（b）所示。本文将采用全局约束Sakeo-Chiba进行相似性度量工作。

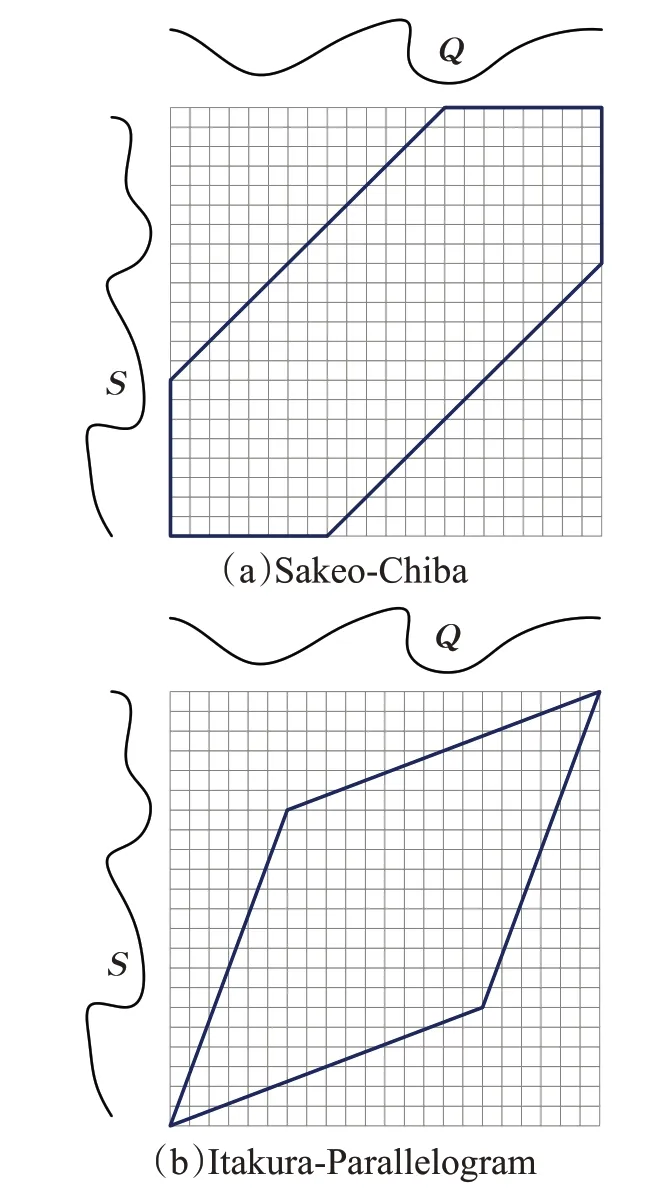
图2 两种弯曲窗口Fig.2 Two warping windows

2.2 基于early stopping的DTW距离度量

提前终止（early stopping）算法原理较为简单易懂。其核心思想为：在本次的距离计算中，若累积距离值达到预期设定的阈值，则立即终止本次计算，并开始下一轮的距离计算，根据此原理来达到节约计算成本的效果。如在计算DTW累积矩阵的某行列单元格，可以不必计算整行或者整列单元格的累积距离，通过这种算法思想来减少计算成本。这种计算方式尤其应用于高维距离计算效果更好[24]。

性质1假设时间序列S={s1,s2,…,sn}，Q={q1,q2,…,qm}，在累积距离矩阵M中，若能够找到唯一的最佳弯曲路径，并且这个最佳路径上的累积距离之和为γ，那么有DTW(S,Q)≤γ。

证明上一章提到过，在累积矩阵中，能够找到一条最优的弯曲路径W=(w1,w2,…,wk,…,wK)，弯曲路径W中的第k个元素定义为wk=(i,j)k，使得由路径W组最小，其中成的累积距离值即为两个序列的点对基距离。由上一节DTW定义可得，DTW距离等于该最小累积距离之和，即DTW(S,Q=)

接下来，将结合early stopping思想对DTW距离度量进行改进。

基于early stopping的DTW改进具体过程如算法1所示。首先给定两个时间序列S、Q；然后，根据这两个序列构成的距离矩阵，计算出代价矩阵对应元素单元格的累积距离γ(i,j)，并与预设阈值ε作比较，若大于该阈值，则停止当前元素之后的所有代价矩阵所在单元格行（或列）的累积距离计算，进而根据其对角线的新的单元格继续开始计算累积距离，直到最后一列停止，并输出最优累积距离值ES_DTW(S,Q)。通过该算法来减小搜索范围，降低了距离度量的计算成本，同时也确保了原本DTW距离度量的精度。

算法1基于early stopping的DTW算法（ESDTW）

接下来，先参考一个例子来进一步了解early stopping在DTW中发挥的作用。图3是S、Q根据DTW距离度量计算构成的代价矩阵，每个单元格表示对应元素的累积距离大小。假设提前终止的阈值ε为26，由于γ(1,2)＞ε，则第一列单元格中γ(1,3)，γ(1,4)都将被排除在外，即不参与距离计算。同理，γ(2,2)=γ(3,2)=32＞ε，则与之所在列的后续单元格代价距离都无需计算。最终，得到该代价矩阵的最优解为γ(6,4)=28，即ESDTW(S,Q)=γ(6,4)=28。

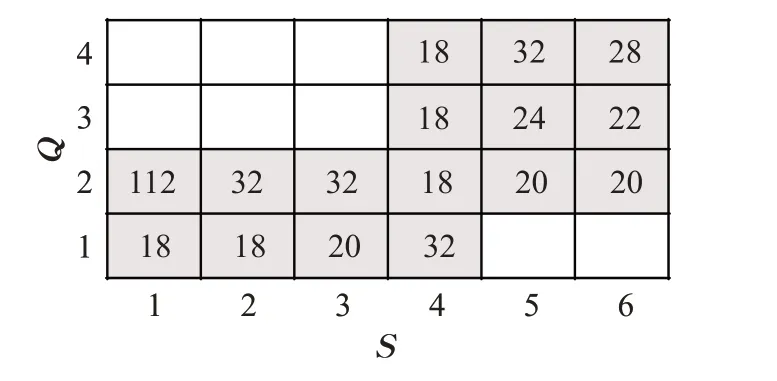
图3 基于DTW距离度量的代价矩阵Fig.3 Cost matrix based on DTW distance measurement

性质2假设时间序列S={s1,s2,…,sn}，Q={q1,q2,…,qm}，在累积距离矩阵M中，该弯曲路径上的累积距离之和为γ，若存在一条最优路径，那么有ESDTW(S,Q)≤γ。

证明参考性质1，由于ESDTW算法进行距离度量的方法与DTW保持一致，那么，在累积矩阵中，同样能够形成一条最佳路径W=(w1,w2,…,wk,…,wK)，使得由路径W组成的累积距离值最小，同理可得

因此，同理可证ESDTW(S,Q)≤γ，即说明了ESDTW距离度量方法的有效性。

Early stopping算法不仅能应用于精确的DTW距离计算，也能在粗略的DTW距离计算中发挥作用，大大降低了计算成本，提高算法性能。

2.3 下界函数方法分析

文中之所以引入下界函数，正因为动态时间规整算法原始时间复杂度过高，如果直接进行两序列之间的DTW距离度量，势必会使得算法的整体的度量效率下降，使得后续的数据挖掘任务变得难以进行下去[25]。下面将对下界函数进行展开分析，并举出代表性的下界函数方法。

首先给出下界函数的定义为，假设存在一个对象O，且它的距离度量函数为M，若某个定义在对象域O上的函数为M"，那么对于所有存在于对象域的参数值oi,oj，总有下列不等式：

如果不等式恒成立，那么将上述M"函数称之为M的下界函数。

如果在度量两个时间序列时，采用度量函数度量其相似度，在没有下界函数参与的情况下，单单依靠距离度量函数只是机械化地将整个样本序列的相似性度量执行完，这种度量的效率较低，时间耗费过大，若加入了下界函数，则能够在度量期间对超过某个预先设定的相似性度量阈值进行比对判断，若实际得到距离值比预设阈值大，那么认定这两条序列是不相似的，相应地也就将其摒弃，也为后续度量节省了时间开销。

那么为了保证下界函数在距离度量函数运行过程中能够有效进行，需满足两个必要条件：

（1）尽量与真实距离度量函数得到的距离接近。因为下界距离函数只是真实距离度量函数的一个先行者，它需要尽可能帮助实际距离度量函数去筛选和过滤掉一些不相似序列，所以下界函数需要更加贴近真实的距离度量函数的边界值，保证度量误差在一个合理范围内。

（2）满足时间复杂度要求，尽可能在O(n)内完成。即下界函数需要在线性时间内完成度量，如果下界函数的时间复杂度超过了实际距离度量函数的计算耗时，那么可以说此下界函数是无效的。

如今的下界函数方法已有很多，典型的主要有：LB_Kim、LB_Yi和LB_Keogh。下面将重点介绍一下LB_Keogh下界函数。

LB_Keogh的提出是为了针对DTW的耗时问题。该方法通过计算候选序列的边界序列来组成动态时间规整距离的下界。设候选序列Q={q1,q2,…,qn}，将全局约束引入到弯曲路径中，边界约束为r，利用参数r定义两个边界序列U={u1,u2,…,un}，L={l1,l2,…,ln}，其中：

U、L分别代表上边界序列和下边界序列，如图4组成了上下包络线与Q的位置关系，而被U、L包裹其中的区域，则称之为封袋。

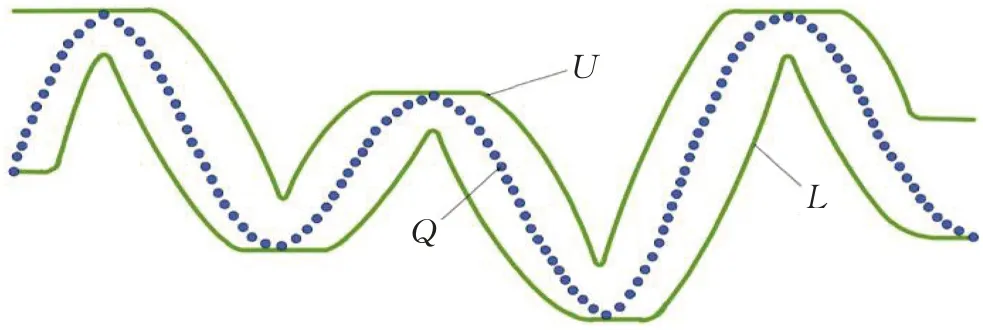
图4 查询序列与其上线边界序列Fig.4 Query sequence and its on-line boundary sequence

其中，包络线上界与下界的一个重要性质为：

进而，得到动态时间规整的下界函数LB_Keogh为：

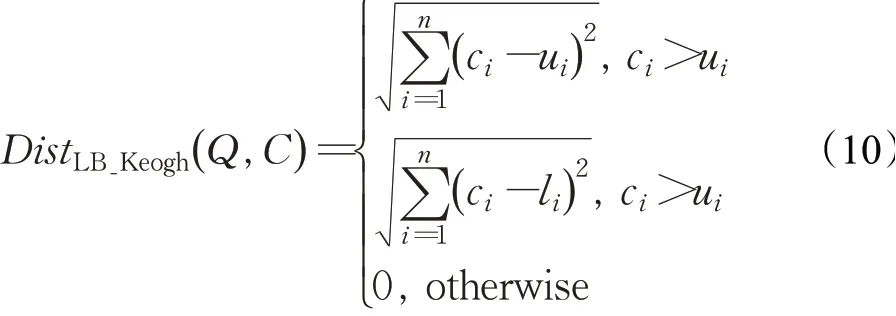
该下界函数可理解为候选序列C中没有落入封袋的点与边界线的距离之和，如图5。

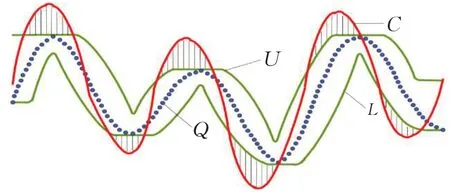
图5 下界距离LB_ESDTW的示意图Fig.5 Schematic diagram of LB_ESDTW with lower bound distance

2.4 基于ESDTW下界距离（LB_ESDTW）

上文提出了一种改进的DTW距离度量方法，即ESDTW，下面将给出该方法的下界距离。

设长度为n的两条时间序列Q、C，其边界约束为j-r≤i≤j+r，则ESDTW的下界函数为：

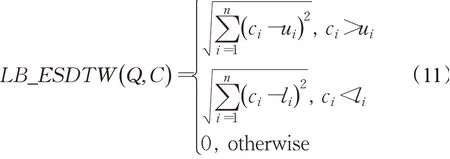
下面首先证明LB_ESDTW(Q,C)≤DTW(Q,C)，即该下界函数满足下界距离引理。

证明在ESDTW度量中，假设Q,C的最佳弯曲路径为W=(w1,w2,…,wk,…,wK)，由上一节对ESDTW的证明可知，其中n≤K≤2n-1，则原命题可转换为：

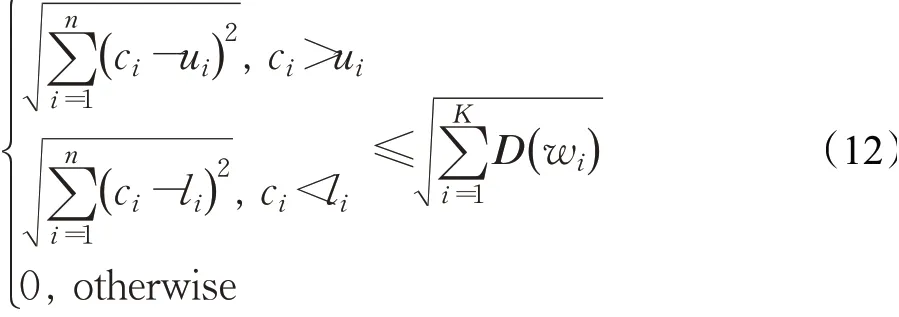
不等式两边平方，得：

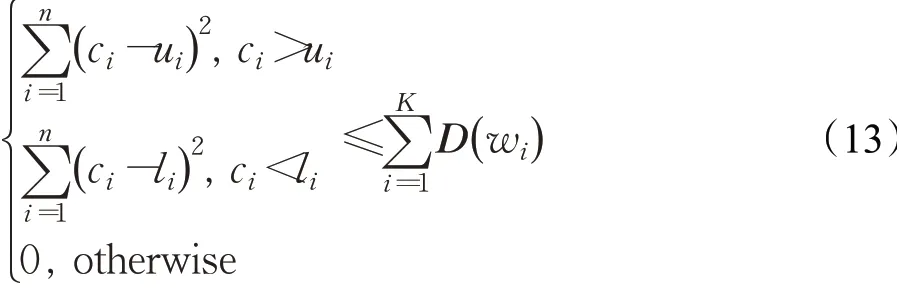
对于式（11），不等式左侧分为3种情况：

当ci＞ui时，不等式左侧第i项为(ci-ui)2，不等式右侧第i项基距离为D(wi)=(ci-qi)2。由于ui=max(qi-r:qi+r)且i-r≤j≤i+r，所以qj≤max(qi-r:qi+r)，即qj≤ui；那么，不等式两边变形后为ci-ui≤ci-qj，又因为左边恒大于0，则不等式两边平方可得因此

当ci＜li，同理可证(ci-li)2≤D(wi)。

当li≤ci≤ui时，显然有0≤(ci-qi)2=D(wi)。

综上所述，不等式（8）成立，即证明了LB_ESDTW(Q,C)≤DTW(Q,C)，该下界距离是有效的。

对于上述下界函数，其计算方法与欧式距离类似，都是通过计算点对点距离的累积和，因此，在计算过程中达到下界函数的最优解ε时，往往会把序列点全部计算完毕才去判断是否满足最优条件，这种计算方式会大大增加时间成本，往往是不必要的。在这里，同样可以将early stopping算法用于下界函数来提高算法的时间效率，采用从左往右依次计算序列点之间的距离，若到达某序列点的距离之和超过了最优解，则终止当前序列计算，因为超过该序列点的计算都将会比ε大，完成整个序列的下界函数计算变得没有意义。

如图6，假设采用下界函数计算到第8个序列点时，该点距离和已经大于最优解了，那么序列点8往后的序列点的计算都将失去意义，由此得出该测试序列与原始序列之间的相似度较低，可将其剔除。通过该方式能进一步提高算法的运行效率，从而降低时间成本。

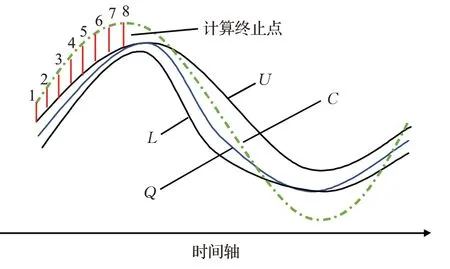
图6 基于下界函数的提前终止方法Fig.6 Early termination method based on lower bound function

2.5 算法分析

下面给出基于DTW下界函数的提前终止算法（LB_ESDTW）。将改进的ESDTW算法1与下界函数相结合，进一步提高了算法的运算效率，大大节省时间成本，同时也保证了后续算法相似性度量的准确性。

算法2基于DTW下界函数的提前终止算法（LB_ESDTW）

算法LB_ESDTW在相似性距离度量方法DTW的基础上采用了提前终止算法，同时在下界距离度量上也在局部增加了提前终止算法，这两次的提前终止算法与下界距离相结合能够提升算法效率。根据算法2的描述和式（11）的计算公式可以得出，长度为n的两条时间序列Q、C进行下界距离度量时，其复杂度为O(n)，内部嵌套提前终止距离度量算法ESDTW，时间复杂度为O(m)，其中m≤n，因而整体算法LB_ESDTW的时间复杂度大小为O(n×m)。而传统的动态时间规整算法（DTW）的时间复杂度则是O(n2)，所以，本文算法的时间复杂度与DTW算法相比，则有不等式O(n×m)≤O(n2)恒成立。当测试数据量较大时，本文的度量算法在时间计算效率上与DTW算法相比将有明显的优势，即大大提高了算法的运行效率，节约了时间成本。该方法对于分类数据维数的大小都能有良好的适应性，不会因为样本数据量大而限制算法的性能。

3 实验与结果分析

为了验证LB_ESDTW的有效性，本文将在特定的时间序列分类数据集上进行实验。对比实验的内容主要针对算法的运行时间测试、下界距离的紧凑性和算法的相似性度量准确率这三部分进行分析。

3.1 实验数据集

本文实验的实验数据集全部来源于Keogh等人提供的来自不同领域的用于时间序列分类、聚类UCR数据集。该数据集中包含了各个领域的不同数据集，里面包含预先处理好的训练集和测试集。本实验共选择了15个数据集进行算法性能测试，这15个数据集的具体特征如表1所示。

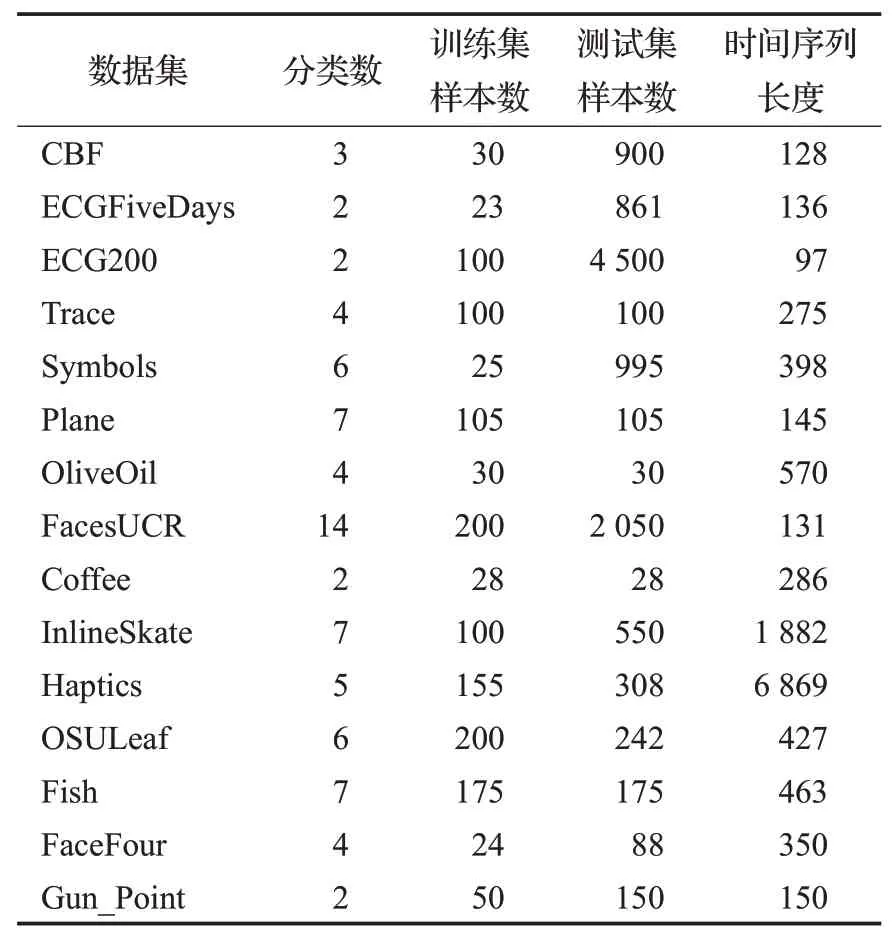
表1 UCR数据集描述Table 1 Description of UCR data set

3.2 实验设置

在实验中，为了验证本文LB_ESDTW算法的性能，分别选取了DTW、LB_Keogh和WDTW三种不同的度量算法进行对比实验。

由于时间序列数据集来自不同领域，彼此的特征值取值范围有一定差距，为了便于对比实验，在采用线性分段算法之前首先对时间序列做规范化处理，将序列特征值规范化到[0，1]之间，其规范化公式如下：

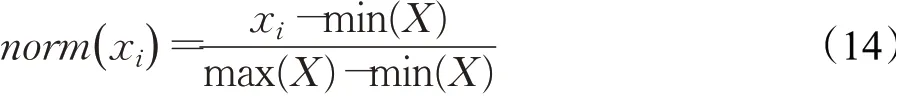
3.3 实验结果

算法运行在2.5 GHz CPU，8 GB内存Windows系统的Python 3.5.1环境下。本文选取了UCR中的10个数据集进行实验，每个算法均进行100次实验，结果取100次实验的平均值。

由于本文采用Sakeo-Chiba全局约束进行时间序列相似性度量实验。首先，为确定实验的具体全局约束参数，将采用LB_ESDTW算法准确率实验来选定具体的全局约束参数R。表2是在时间序列都为原始序列长度的情况下，且保证全局约束在10%≤R≤50%范围内进行准确率实验。目的是探究全局约束R取何值，时序的度量准确率达到最高。其中，标粗数据是当前数据集下得到的最高准确率所对应的全局约束。从表2列出的准确率数据可以看出，在测试的15个数据集中，有4条数据集在R=10%时算法准确率达到最优；有5条数据集在R=15%时算法准确率达到最优；有4条数据集在R=20%时算法度量准确率达到最优；有2条数据集在R=25%时算法准确率达到最优。综合这15个数据集的算法准确率来看，整体趋势都是先逐渐上升到某个峰值（算法准确率达到最高）再逐渐下降，且当全局约束R越大，准确率下降幅度也随之变高。因此，根据这一参数特性，可以得出算法的全局约束参数值在10%≤R≤25%这一范围内能得到最优准确率。而在实验中，只需在算法中加一个记录判断环节，即加一个for循环和if判断得到当前数据集下的全局约束最优解。

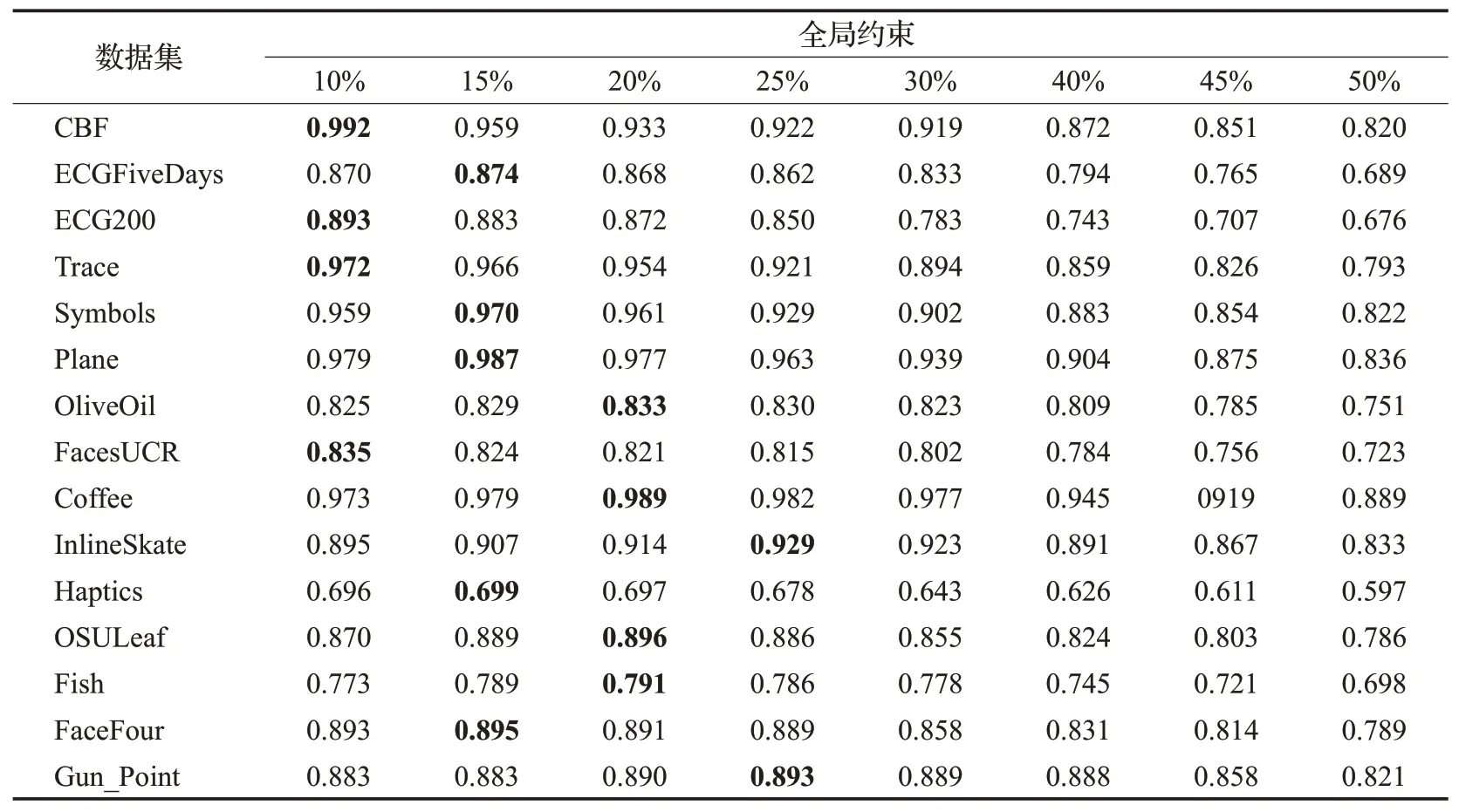
表2 全局约束下的LB_ESDTW算法准确率Table 2 Accuracy of LB ESDTW algorithm under global constraints

实验1算法的运行时间分析

在本实验中，选取UCR训练数据集中的CBF、ECGFiveDays、ECG200，Coffee这四个数据样本的第一条样本序列与测试序列进行相似序列搜索的运行时间的对比分析。通过分析上述四种算法在边界约束r取不同值时，即取序列长度压缩率为10%～100%时的弯曲范围，得到不同的运行时间，从而得出各个算法的运行效率。那么，边界约束与弯曲范围的关系为r=N×w×100%。其中，r为边界约束，N是时间序列长度，w为弯曲范围。由于r和w成正比，所以在本实验中，将采用弯曲范围w与运行时间t进行实验分析。

如图7，分别在上述的三个数据样本下进行四种算法的弯曲范围w和运行时间t的对比实验。

从图7对比可以看出本文算法都有最低的时间消耗，即本文的LB_ESDTW算法在四种数据集下的运行时间都为最短，从侧面反映了该算法的运行效率较高。

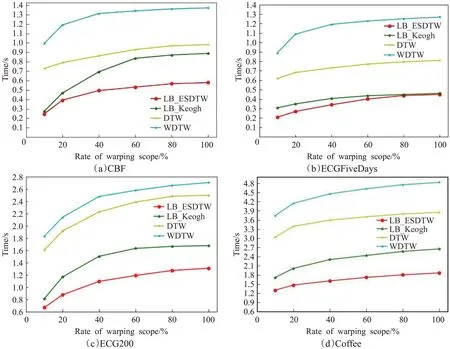
图7 不同弯曲范围下的运行时间Fig.7 Running time under different warping ranges

实验2下界距离LB_ESDTW的紧致性分析

算法的紧致性越好，说明下界距离更接近实际距离，使得在使用下界距离进行相似性度量时，得到的误报序列更少，更精确地匹配到相似序列，同时保证了准确率。本实验采用紧缩率和修剪率这两个性能指标来度量下界距离LB_ESDTW的紧致性。下界距离LB_ESDTW的紧缩率SESDTW定义为：

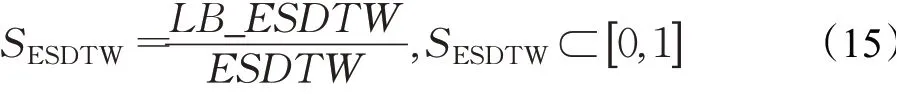
修剪率P定义为：

其中，N0为在下界距离LB_ESDTW的过滤筛选下得到的不需要与训练集样本进行相似性度量的序列数量，N为该数据集的总样本序列数。

本实验选取了上述15个UCR数据集进行紧缩率分析。对同一数据集进行多次紧缩率实验记录并最终选取紧缩率SESDTW的平均值，具体实验结果如表3所示。

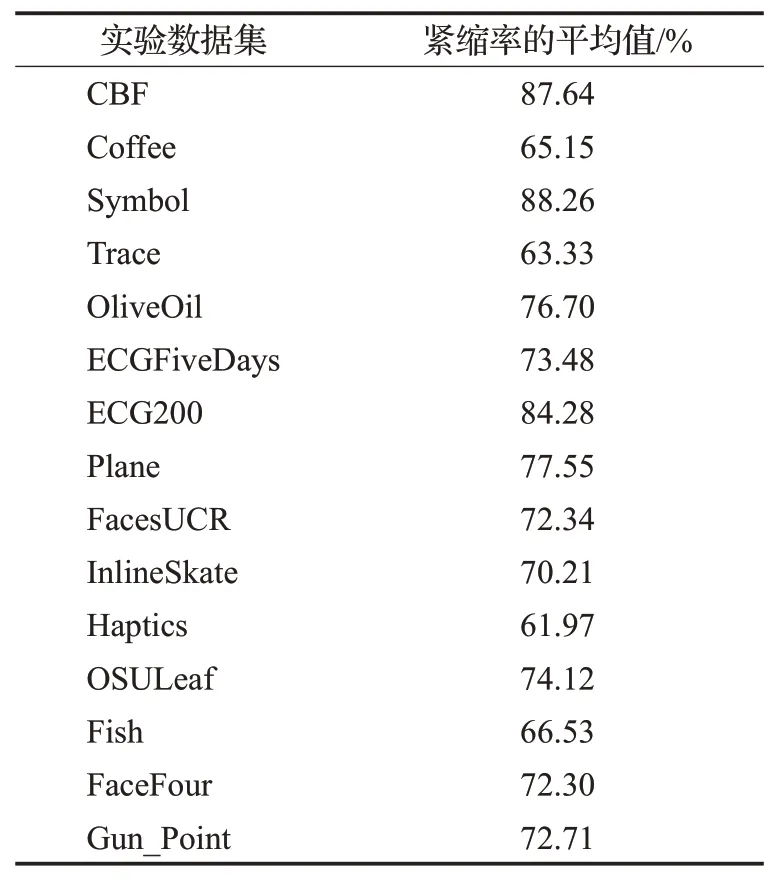
表3 下界距离LB_ESDTW的紧缩率Table 3 Contraction rate of LB_ESDTW with lower bound distance

本实验选取了其中的六个数据集对修剪率在边界约束r取不同值时进行分析，实验结果如图8。

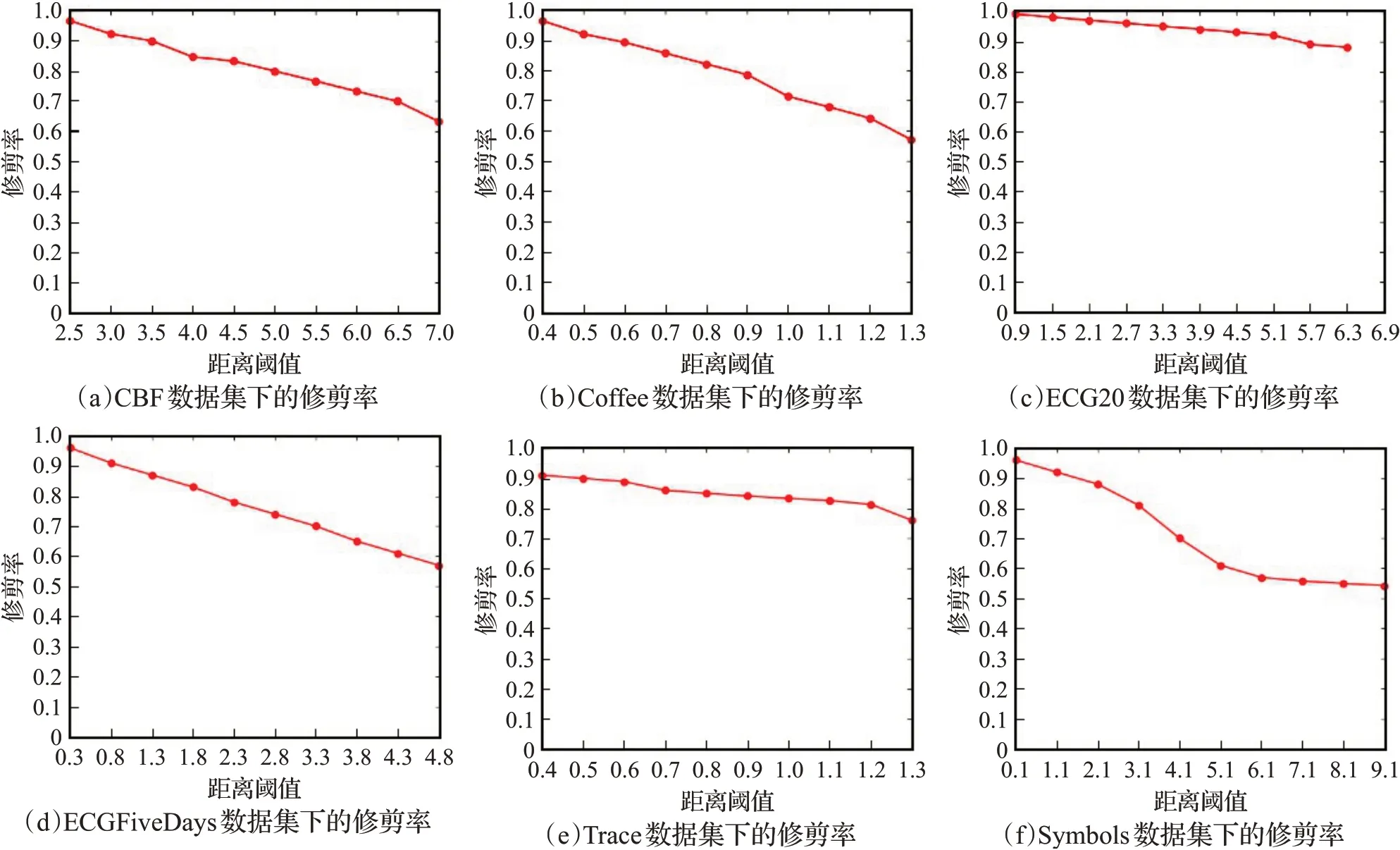
图8 下界距离LB_ESDTW的修剪率Fig.8 Pruning rate of LB_ESDTW with lower bound distance

在第一个紧缩率实验中，下界算法LB_ESDTW在五个不同数据集下的紧缩率都在50%以上，也就证明了该下界距离算法的紧致性较好；在第二个修剪率实验上，该算法在距离阈值较小时的修剪率都能达到70%以上，而当距离阈值逐渐增加，相应的修剪率则随之减小，由此得知下界距离LB_ESDTW的修剪率和距离阈值存在一定的关系，即当距离阈值过大，超出了ESDTW距离时，意味着该下界距离失去了原有的过滤筛选作用。综上两个对于紧凑性判断标准的实验结果，能够明显看出该算法的紧凑性较好。

实验3算法准确率对比实验

本实验中，将本文下界算法LB_ESDTW分别与其他相似性度量方法进行算法的分类准确率对比实验，目的在于分析各算法之间的相似性度量准确率，从而判断本文所提算法的相似性度量性能。

本实验采用上述15个不同领域的数据集进行对比实验。进行对比的相似性度量算法分别有ED、DTW、LB_Keogh、WDTW以及本文算法LB_ESDTW。同时保证这五个算法在不同数据集下的边界约束r都是压缩率在100%的弯曲路径。

表4给出了在上述描述的15个不同数据集下的各算法的相似性度量的分类准确率。

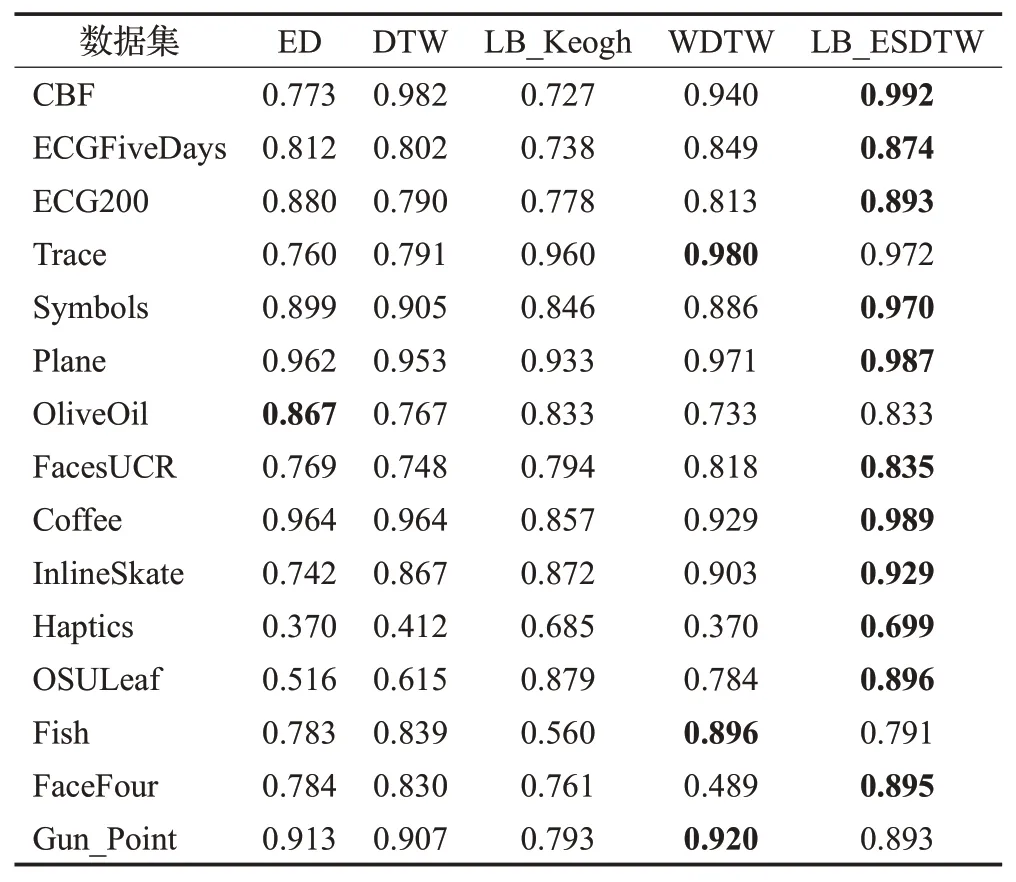
表4 算法度量的分类准确率Table 4 Classification accuracy of similarity measure

表4中用粗体表示的数据为算法在当前数据集下获得的最高分类准确率。从表4的分类结果不难发现，对于所选的15个数据集来说，其中LB_ESDTW算法在11个数据集的分类结果都优于其他四种算法的分类结果，也表明了LB_ESDTW下界距离度量的分类性能较好。

4 结束语

本文给出了一种基于early stopping思想的DTW距离度量，即在计算两个序列的距离时，发现本次计算所积累的距离信息已经足以判断结果，则终止本次计算，大大降低了计算成本；并在下界距离函数LB_Keogh方法基础之上，提出了一种基于DTW下界距离函数的提前终止算法，实现了算法在DTW距离度量和下界函数距离度量相融合的相似性度量，同时也提高了算法的适应性。通过在UCR数据集上的三种对比实验，表明其在时间计算成本低、算法的紧致性良好且算法的分类准确率高的特点。本文已在大多数时间序列数据集下进行实验论证，由于数据集的时效性和局限性，后续将通过更多不同领域的时序数据集来验证本文所提算法的有效性。同时，为了能够更好地平衡算法的度量准确率和时间效率，接下来的工作主要是将时间序列的表示方法与相似性度量方法结合起来，并根据数据挖掘的任务需求，设计出针对不同场景的具有普适性的融合度量查询系统，如针对病人的心电数据，设计一种实时在线的度量系统；而针对股票趋势的分析，则设计出一种预测度量系统模型，以此将本文度量方法在数据挖掘中的优势发挥到最大化。