聚焦新高考“创新性”研究 培养命题创新意识——第二届命题征集活动解析几何专题优质创新试题选登

甘肃 罗文军 彭长军

所以c=2，所以黄金双曲线C的焦距长2c=4.

【创新点分析】本题以传统文化为背景，考查双曲线的离心率，以黄金分割双曲线为依托，考查双曲线的标准方程和焦距，考查方程思想、阅读理解能力、逻辑思维能力和创新能力以及数学文化素养，考查数学运算和直观想象的数学学科核心素养.

(作者单位 姓名：甘肃省秦安县第二学校 罗文军)

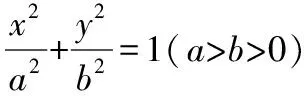
【解题思路】解法1：由椭圆的定义，得|PF1|+|PF2|=2a.在△PF1F2中，由余弦定理，得

4c2=|PF1|2+|PF2|2-2|PF1||PF2|cos60°=(|PF1|+|PF2|)2-3|PF1||PF2|=4a2-3|PF1||PF2|.

由基本不等式，得

∴4c2≥4a2-3a2=a2,

当|PF1|=|PF2|=a时，y0=±b，

所以4b2c2≥3(a2-2c2)2，

即4(a2-c2)c2≥3(a2-2c2)2=3(a4-4a2c2+4c4)，

化简整理，得16c4-16a2c2+3a4≤0，

两边同除以a4，得16e4-16e2+3≤0，

此时P(0,b),∴|PF1|=|PF2|=a,以下同解法1.

解法4：根据对称性，不妨设点P在椭圆的上半部分，直线PF1的倾斜角为α,直线PF2的倾斜角为β，则β-α=60°，且∠PF1F2=α，∠PF2F1=180°-β.

在△PF1F2中，由正弦定理，

由α是△PF1F2的一个内角，知0°<α<120°,

【创新点分析】本题主要考查椭圆的相关知识以及其他知识(余弦定理、基本不等式、三角函数及三角形面积公式等)的综合应用.考查运算求解能力和逻辑推理能力.考查数学运算、逻辑推理的核心素养.试题以椭圆为主干，将多个知识点紧密联系在一起，通过设问考查椭圆的定义及性质、余弦定理、基本不等式、平面向量数量积的定义及坐标表示、三角函数及三角形面积公式、比例的有关性质等知识的应用.试题难易适中，具有一定的区分度，属常规题.在第一个空(最小值)后，不失时机地增加了第二个空，进一步考查取得最小值的条件及三角形面积公式的应用.

(作者单位 姓名：甘肃省嘉峪关市第二中学 彭长军)

【解题思路】解法1：设直线F1P的方程为y=k(x+c)(k>0)，即kx-y+kc=0(k>0).

1.政策逐渐削减导致电动汽车发展必将由政策驱动转向市场牵引。政策扶持力度削弱后，市场会进行再定位，在没有政策扶持的诱惑，以及失去地方区域市场优势和政府干涉的非自然状态下，电动汽车将恢复到市场定位，电动汽车市场中的企业更倾力于增强供给侧的能力，关注顾客要求，不断增强自身技术，使市场竞争环境更加真实。

即16a2c2=21b2(c2-a2)=21(c2-a2)2，

化简整理，得21c4-58a2c2+21a4=0，

两边同除以a4，得21e4-58e2+21=0，

本题也可画出符合题意的图象(如图)，利用平面几何知识并结合斜率的定义求解,过程如下：