基于演绎推理的一个数除以分数学习路径研究*

□ 张 希 张 丹 邵汉民 巩子坤

一、引言

本文在前文研究“分数除以整数”［1］学习路径的基础上，继续以学习路径为工具，探索一条基于演绎推理的“一个数除以分数”的学习路径。

主要探究以下问题：（1）基于演绎推理的一个数除以分数的学习路径是什么？（2）基于演绎推理的一个数除以分数的学习路径可行吗？

二、研究设计

（一）研究步骤

在萧山区XH 小学的甲、乙两个班继续开展研究，研究对象与研究流程同前文。

（二）问卷设计

实验班后测例题如下：

对照班后测例题如下：

测试后对问卷进行赋分，计算正确得1 分，说理正确得3分，满分4分。

三、研究结果与分析

（一）一个数除以分数的学习路径：初构

1.路径呈现

基于我们的研究［2］与上一篇文章的内容，初构了学习路径B1（如图1）。

图1 初构的学习路径B1

任务一借助直观表征“画一画”即可说明算理。

任务二中直观表征难度增加，由此回顾形式表征“推一推”。此时，通过“设、化、消、传”等方式帮助学生巩固“推一推”，同时让学生感悟：当表征一个数除以分数的算理时，直观表征会随着任务难度的提高而变得越来越复杂，但形式表征无论难度高低均能适用。

任务三完全符号化，将具体的数字转化为字母，化“举例”为“一般”，形式表征的优势得以显现。

本节课的目标是：感悟符号的一般性、算理与算法的一致性；探究算理，经历演绎推理的过程。上节课，学生不熟悉演绎推理，所以由老师带领学生探究算理。本节课的演绎推理本质上与上节课是一致的，故重点落实于“放手让学生探究算理”。下文将借助部分教学片段，说明如何落实以上目标，其中T是授课教师，S是学生。

S：我先将算式的答案设为“？”，根据除法是乘法的逆运算，将分数除法转化为分数乘法；根据等式的基本性质，将等式左边“？”的系数消去；最后，根据等式的传递性，得到（ 如图2）。

图2 任务三板书

T：由此我们可以得到什么结论？

S：除以一个不为0 的数等于乘上这个数的倒数。

2.存在问题与改进建议

随着分数除法越来越复杂，研究团队开始思考：能否使“推一推”更一般化？如何进一步提升第二节课的思维高度？“颠倒相乘”仅仅适用于分数除法吗？能否将“推一推”运用于所有除法？

为解决上述困惑，增加任务四：玻璃杯的容量是bL。现有aL 牛奶，可以装入多少玻璃杯？实际上，“颠倒相乘”不仅仅适用于分数除法，还适用于小数除法、整数除法等有理数除法，且都能通过“推一推”来证明。所以，不妨在课堂上“一推到底”，将分数除法课上成一堂涵盖所有有理数除法的算理课。

任务四只有两个字母a、b，可以表示任意有理数，相对具体数值，更清晰、更具普适性，学生也更易理解。学生在解决任务四的过程中，感悟到：分数除法与整数除法、小数除法不仅算理是一致的，算法也是贯通的。

（二）一个数除以分数的学习路径：优化

1.路径呈现

相比于初构的学习路径B1，优化的学习路径B2（如图3）新增了任务四，这也是整节课的难点：从分数除法过渡至有理数除法，实现算理贯通。教学实录如下。

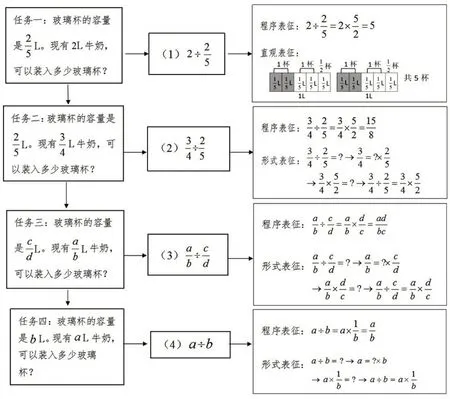
图3 优化的学习路径B2

T：回顾两节数学课，大家认为可以给这两节课取什么标题？

S：分数除法，分数除以分数，除法……

多媒体作为一种综合性较强的教学媒体，它不仅可以提供视觉信息，还可以传递听觉信息。所以，在大学普通化学教学中应用多媒体进行辅助教学，不仅可以使原本枯燥乏味的化学课堂变得更加生动有趣，还能使原本丧失化学学习兴趣的学生变得更加积极主动。可见，详细研究多媒体辅助教学与大学普通化学教学改革是很有必要的，它在一定程度上能提高教学的质量与效率。

T：有的同学说是除法，那么老师写一个除法算式9÷4。这个算式和我们推过的算式不一样，那么“颠倒相乘”还适用吗？（学生产生意见分歧）谁能到黑板上来推一推？

图4 学生板书

S：分数除法“颠倒相乘”也适用于整数除法。

T：那么，小数除法0.4÷2适用吗？

S：也可以！

T：现在能给这两节课取一个标题了吗？

上述教学片段使学生加深了对除法的认识，践行了“算理贯通、算法统整”的理念。本节课将“推一推”进行到底，渗透“寓演于算”的思想，帮助学生厘清除法的本质。

将除法算理聚焦于a÷b，不仅使教学更简洁，内容更简约，也使学习更简便：学生可以通过一个算理统整除法运算，降低了认知难度，减少了认知负荷。分数除法的学习不再是一个机械记忆法则的过程，不再是一个知其然而难知其所以然的过程，渐渐成为了一个培养演绎推理能力的过程，进而达到算理贯通、理法互融。

2.教学效果

对甲、乙两个班学生的后测平均分进行独立样本t检验，结果显示，甲、乙两个班的得分（t=1.796，P＜0.05）存在显著性差异。这说明优化的学习路径B2得到了改进。

为进一步了解优化的学习路径B2 的教学效果，对学生进行访谈，访谈中发现：几乎所有学生都能理解为何要进行推理以及“推一推”中每一步的目的和原理；超过半数的学生能感悟推理的优越性、字母的一般性。这样的掌握程度正是研究设计之初所期望达到的效果，说明基于演绎推理的分数除法学习路径是行之有效的。

（三）学习路径的整体效果

1.实验班、对照班后测数据分析

对“实验班”“对照班”学生的后测平均分进行独立样本t检验，结果显示，对照班、实验班的得分（t=2.734，P＜0.05）存在显著性差异。综上所述，与教材中的学习路径相比，本研究设计的学习路径更利于学生理解一个数除以分数的算理。

2.实验班延迟后测数据分析

延迟后测数据表明，相比即时后测，甲班的延迟后测得分率降低了44.27%，乙班降低了15.87%；且乙班的延迟后测得分明显高于甲班，相差39.08%。这说明乙班的教学效果更持久，学生的遗忘率有效降低，即优化的学习路径B2 更具有延迟效应和可行性。

四、分析与讨论

（一）基于演绎推理的分数除法学习路径具有可行性

教学实验发现，相对于对照班的学生，实验班的学生很好地掌握了分数除法的算理，说明该路径具有可行性。实验取得良好的结果，有以下两点原因［3］：第一，六年级学生已经具备推演分数除法的前提知识。第二，演绎推理具有简洁性。缩短了教学课时，减少了不必要的练习；同时也表现在学习的简便上，学生通过一个算理、一个算法统整了有理数除法，降低了认知困难，减少了认知负荷。

（二）学习路径的创新之处

1.凸显演绎推理的必要性

利用字母引起学生的认知冲突，遵循“个别举例—提出假设—证明假设”的探究顺序，合理引入演绎推理，实现从直观表征到形式表征的自然过渡。

2.感悟符号的一般性

3.感悟除法运算的一致性

分数除法不仅与整数除法、小数除法的算理是一致的，算法也是贯通的。本学习路径一以贯之地推演除法算理、推导除法算法，渗透“寓演于算”的思想，最终实现贯通算理、统整算法。

（三）构想：分数除法教学可缩短至一课时

五、结论与建议

（一）结论

研究数据表明，本研究设计的学习路径具有可行性。与教材中的学习路径相比，本学习路径更利于学生理解一个数除以分数的算理，并利于实现除法运算算理贯通、算法统整。

（二）建议

教材可以参考我们得到的优化的学习路径B2：借助演绎推理，引导学生理解分数除法算理；借助简洁的字母符号，凸显特殊与一般的关系；强调算理的贯通，统整整数除法、小数除法和分数除法的运算。

教师教学时，由于学生已熟悉演绎推理的过程，所以本节课要放手让学生探究算理，体验演绎推理的过程。同时，教师要处理好对演绎推理规范性的要求：要求学生掌握基本原理和步骤；明确推理的意图；提出恰当的要求，无须苛求过程的规范。