促进数学学习可持续发展的探究
郑平平
(安徽省蒙城第一中学,233500)
可持续发展是一个社会学概念,其核心就是当前的社会活动要服务于今后长期发展的需要.数学教学也应该有如此观念,即现在的教学活动不能只考虑一节课、一个知识点、一个单元的教学任务,而要着眼于学生的整个学习阶段,甚至于学生终身发展的需要.从这一点来讲,学生的学习兴趣、学习习惯、素养提升、能力提高就应该是当前教学的目标.本文对数学学习可持续发展理念进行思考与探索,供参考.
一、培养学习兴趣
由于数学是从自然现象中抽象出来的,这个抽象过程是伴随着好奇心驱使的结果,所以保持学习兴趣是学好数学的重要保证.数学中的每一个知识点,从概念到性质再到运用都有一个思维过程,理解并熟悉这个过程是最好的记忆方式.
例如弧度制的形成.在初学三角函数时,一般人都会认为:三角函数既然是函数,那么自变量和函数值都是实数.但三角函数的自变量是角度,与常规的实数是不一致的,而且不如实数那样方便表示.如何解决如此问题呢?科学家们想到,一个角与一个扇形类似,也就是说一个角可以看成是圆的一部分.联想到圆的周长与圆的半径的关系,即圆的周长与其半径之比总是定值π.如果此圆是单位圆,则圆的周长就与周角对应,那么单位圆的一段弧长就表示一个角的大小.这样也就容易理解用弧度制作为一个角的测量单位了,同时也容易理解和记忆角度制与弧度制之间的换算关系.学生对如此缘由和来龙去脉肯定是感兴趣的.
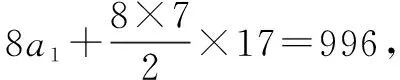
在课堂教学中,不失时机地充实这样的一些内容,很容易吸引学生的注意力,活跃课堂氛围,拉近师生关系,使学生愿意听或者是喜欢听数学课.学生的兴趣有了,这样学习的效率就自然会提高了.
二、形成质疑习惯
质疑是一种重要的认知习惯,只有对某一种现象不断质疑,才能真正认清并理解事情的原委,才有进一步弄清真相的动力.在数学学习过程中是最需要反复质疑的.高中学生也有了一定的质疑能力,所以引导学生针对主要问题、核心内容进行质疑、辩论,可增强对某些概念的认识,增强对某些解题思路、解题方法理解.
例如,在讲函数奇偶性定义时,有些同学对定义的前提条件往往不注意,只看重后面:若f(-x)=f(x),则函数f(x)是偶函数;若f(-x)=-f(x),则函数f(x)为奇函数.在做题时只验证,f(-x)与f(x)的关系就判断其奇偶性.课堂上要引导学生质疑,通过举反例:判断函数f(x)=x2{x∈(0,2)}的奇偶性,并画出此函数的图象,可知f(x)在(-2,0)的图象不存在,从而确定此函数不具有奇偶性.这样可使学生深刻地认识到,判定函数的奇偶性首先应验证定义域是否关于原点对称.
三、着力素养提升
一个学生的数学素养包含多个方面,其核心内容就是能将实际生活中的一些现象和遇到的问题抽象成数学模型,然后再用所学数学知识解决问题.当然这种素养不是一蹴而就的,需要循序渐进,逐步提高.一般来说,随着数学知识的丰富,素养就会越高,能力也会越强,但需要在数学学习过程中不断地提高,老师的及时点拨、悉心指导会起到关键的作用.
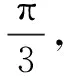
(1)设OA=akm,OB=bkm,试用a,b表示新建公路AB的长度,求出a,b满足的关系式,并写出a,b的取值范围;
(2)设∠AOT=α,试用α表示新建公路AB的长度,并且确定A,B的位置,使得新建公路AB的长度最短.

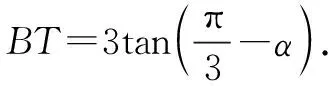
这是一个解三角形的应用题,重点是让学生认识和感受问题、理解问题、分析并解决问题,教师只是在关键时刻进行适当的点拨和注意点的提醒.
四、挖掘探索能力
学生能否得到可持续的发展,其继续学习的能力很重要,这里不仅是知识的增加,运用所学知识解决问题的能力要得到提高,还要求分析探索、判断规划的技能必须具备.所有这些都需要在课堂教学中,潜移默化、聚少成多,才能见到效果.所以,每一次的备课、每一道例题的讲解都需要精心准备,有的放矢,争取每一堂课都能让学生有所收获.
例2已知函数f(x)=lnx-ax,g(x)=ex,a∈R.
(1)若函数y=f(x)-g(x)在区间(1,+∞)上为单调函数,求实数a的取值范围;
(2)设H(x)=|f(x)|g(x),x∈[1,e],若H(x)在定义域上有极值点,求实数a的取值范围.
解析第(1)问比较容易,设h(x)=f(x)-g(x)(x≥1),分h(x)单调递增和调递减讨论解决,易得a∈(-∞,-e]∪[1-e,+∞).
上面的例2把一个复杂问题,通过分类讨论,转化为若干个小问题来求解,整个解题过程就是探索前进的过程.这种探索能力的提高,对今后的继续学习以及今后人生的发展都有很大帮助.
关注学生的可持续发展是一个系统工程,作为一个数学老师,除了要完成这个阶段知识点的教学任务,还要潜心研究如何让学生在数学方面持续发展,这也对下一个阶段的教学工作有较大的促进作用.

