基于火药燃烧模型的弹射器工作过程数值模拟

刘 群，蔡文健，杨 昭，周传霞

(北京空间机电研究所，北京 100076)

0 引言

火药燃烧产生的高温燃气是大多数火工装置工作的能量源，因此火药燃烧特性是决定火工装置工作性能的关键因素[1]。然而，火工装置作动是一个高速瞬态过程，很难通过试验获得火药燃烧和机械部件相互作用甚至发生破坏的细节。因此，建立火药燃烧模型有助于解释试验结果，并有助于产品的设计改进。数十年来，国内外学者对火药燃烧模型及其结构的作用过程进行了大量研究。Ng[2]开发了最早火工装置驱动模型，称为MAVIS，其中燃烧过程引起的质量和能量释放并没有直接建模，而是使用经验公式确定的状态方程来描述驱动活塞运动的压力。Emery等[3]和Jones等[4]采用相同的方法对电爆阀内活塞运动的过程进行了建模计算。此后，研究者开始考虑火工装置内火药燃烧反应过程。他们的模型考虑了火药燃烧释放到气体和凝聚相产物的能量随时间的变化过程，但是这些能量在容腔内都是均匀分布。该模型由一系列以时间为变量的常微分方程组成[5-12]。以上学者建立的模型均假设火药燃烧反应速率比装置工作时间小得多。Lee[12]的工作探索了密闭容器内非稳态气体动力学对装置工作过程的影响，结果表明，当装置工作时间与燃烧波传播时间接近时，能量空间均匀分布假设无效。然而，Lee的模型未考虑火药燃烧释放能量过程，仅是将高压不连续性能量入口作为模拟燃烧的初始条件。因此，以往的模型在预测和分析火工装置性能时，没有同时考虑火药燃烧的能量释放过程和燃烧腔内的压力梯度分布。本文借鉴炸药反应的多项式模型，建立了单项式火药燃烧模型，模型能够定量描述火药燃烧过程以及容腔内的压力分布，采用该模型对弹射器工作过程进行了数值模拟计算，计算结果与试验结果吻合性较好，表明该燃烧模型能够较真实地描述火药燃烧过程，可以将该模型用于指导火工装置设计。

1 单项式火药燃烧模型

火药燃烧反应是以燃烧波形式传播，经典的火药燃烧过程如图1所示。假设火药从左端点火，则会产生一个平面燃烧波向右传播，燃烧波逐渐传入未燃烧火药，同时燃烧产物留在燃烧波后面，在未燃烧火药和燃烧产物之间有一个相对宽的燃烧反应区，火药在反应区内发生气化并且反应。

图1 经典火药燃烧过程示意图Fig.1 Scheme of classic propellant burning

燃烧反应区前沿主要通过热传导和分子扩散引燃未反应火药，未反应火药进入反应区后通过化学反应速率控制反应程度，反应完全后进入反应产物区。因此，燃烧反应区宽度可以由宏观传质过程和微观反应过程决定。基于以上分析结论，本文将火药燃烧模型划分为未反应状态方程、宏观燃速方程、微观反应速率方程和反应产物方程；火药燃烧通过宏观燃速控制燃烧波前沿速度，即不同位置火药的起燃时间，然后通过微观反应速率方程控制起燃火药的化学反应速度，从而唯象地描述火药燃烧反应区现象。

宏观燃速方程主要是建立燃速与压力的指数关系，此方程源于经典的火药几何燃烧模型。

u=BPn

(1)

微观反应速率方程主要是建立反应速率与压力的关系，此方程源于炸药多项式反应速率方程。

(2)

反应产物状态方程主要是采用范德瓦尔斯气体状态方程，用以描述高压下反应产物的压力变化。

(3)

式中,u为宏观燃速，P为燃气压力，ψ为燃烧分数，R为气体常数，T为燃气温度，V为比容，ρs为火药密度，A，B，R1，R2，n为常数。以上3个方程联立，可以描述火药经历化学反应生成反应产物的过程。

2 火药燃烧模型参数拟合

火药燃烧模型涉及的参数较多，且部分参数并无物理意义，因此，确定模型参数是准确描述火药燃烧特性的前提。常用的试验方法一般采用密闭爆发器测压，即在一个已知容积的密闭容器内测定一定质量火药燃烧产生的压力曲线，然后采用火药燃烧模型进行仿真计算，将计算结果与试验结果进行反复拟合，最终确定火药燃烧模型的参数。

典型的密闭爆发器试验示意图如图2所示。试验装置由点火器、主装药、密闭容器和压电传感器组成。当点火器接收到电信号后，点火器起爆主装药，主装药燃烧产生高温高压燃气，通过压电传感器记录密闭容器内压力时间变化曲线。试验中，密闭爆发器容腔为10 ml，采用两个压电传感器记录压力变化曲线，点火器10 ml容腔的输出压力在10 MPa左右，被测主装药为SL17双基推进剂。

图2 密闭爆发器试验装置示意图Fig.2 Geometry of closed vessel test

根据密闭爆发器结构，建立了其计算模型，如图3所示。计算模型对物理模型进行了简化，仅考虑空气域和火药，点火器通过定义能量入口来模拟。计算中，能量入口以压力形式向容腔内注入一定压力，当压力达到一定值时，火药被引燃，火药不断燃烧导致容腔内压力逐渐增大，直至火药燃烧完毕，计算过程中考虑壁面散热影响。

图3 密闭爆发器计算模型图Fig.3 Numerical model of closed vessel

3 模型验证

为了验证火药燃烧模型及参数的准确性，建立弹射器计算模型，对弹射器工作过程进行数值模拟计算，获得弹射器弹射速度，并且与试验结果进行比较，验证计算准确性。

弹射器结构示意图如图4所示。弹射器主要由外筒、内筒、活塞、滑杆、火药、点火器和剪切销组成。点火器接到电信号后引爆，点火器火焰起爆主装药，主装药燃烧产生高压燃气，当燃气压力达到一定值时内筒剪断剪切销开始运动，最终以一定速度飞出外筒。根据装置物理模型，建立弹射器计算模型，计算模型对物理模型进行了简化，点火器通过能量入口实现，剪切销通过在内外筒之间设置连接力实现。模型中内筒、外筒、活塞和滑杆材料均为钢，采用弹塑性材料模型描述；火药为SL17，药量为100 mg，采用火药燃烧模型描述，剪切销连接力为2 000 N。弹射器计算模型图如图5所示。

图4 弹射器结构示意图Fig.4 Geometry of the catapult

图5 弹射器计算模型Fig.5 Numerical model of the catapult

4 计算结果与分析

4.1 SL17模型参数

SL17火药参数拟合的基本过程为：首先输入一组火药燃烧模型参数进行模拟计算，将计算获得的压力曲线与试验结果进行比较，根据比较结果调节相应参数，再次带入模型进行计算，反复调节，直至模拟结果与试验结果基本吻合，最后确定的一组参数可以用来描述SL17火药的反应过程。

密闭爆发器计算过程中压力云图如图6所示。从图6中可以看出，在燃烧开始后1.5 ms时，容腔内最大压力为38 MPa，最小压力为37.3 MPa，表明容腔内压力均匀性较好，燃烧产生的燃气有足够的时间在容腔内扩散，可以将容腔内气体作为均压状态，因此，容腔内各位置的压力变化历程基本相同。在容腔内任意选择一点监测压力变化过程，将计算结果与试验结果进行对比，如图7所示。从图中可以看出，试验曲线的初始阶段，压力在短时间内有一个突跃，这是点火器起爆后引起容腔内压力迅速增加，突跃后压力曲线缓慢上升，表明火药开始燃烧；在2.2 ms时，容腔内压力达到峰值55 MPa，此后，容腔内压力基本维持恒定，表明火药燃烧完全。因此压力曲线可以分为两段，初始压力突跃段为点火器燃气压力输出段，突跃段之后压力上升段为火药燃烧燃气压力输出段。由试验曲线与计算曲线对比看出，只是在初始段两条曲线有一定差别，在火药燃烧段两者吻合性较好。这是由于点火器的输出特性与模型中简化的能量入口有一定差别，能量入口的输出速率较低，而点火器输出速率较快。总体而言，模型对火药燃烧段的计算结果与试验结果吻合性较好，表明模型可以很好地反映火药的燃烧特性，最后拟合得到了SL17火药的模型参数，如表1所示。

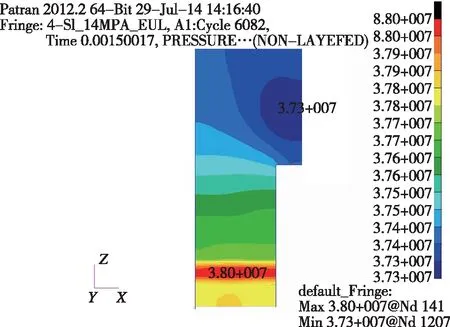
图6 计算过程中压力云图Fig.6 The calculation pressure contour

图7 计算曲线与试验曲线对比Fig.7 Comparison between calculation and test curve

表1 模型参数表Tab.1 Model parameters of SL17

4.2 弹射器工作过程计算

将拟合得到的参数代入弹射器计算模型进行计算，验证模型及参数的准确性。不同时刻弹射器运动过程如图8所示。从图8中可知，0.17 ms时，容腔内的火药开始燃烧，容腔内压力开始升高，此时容腔内最大压力为5 MPa左右，火药燃气对活塞的推力仍小于剪切销剪切力，因此活塞并未开始运动；随着火药燃烧量的增加，容腔内压力逐渐增大，当某一时刻，容腔内压力大于剪切销剪切力时，剪切销被剪断，活塞开始推动滑杆运动；在1.03 ms时，活塞与滑杆组合体撞击内筒，此时容腔内最大压力在11 MPa左右，此后活塞、滑杆和内筒的组合体开始一起加速运动；在1.29 ms时，活塞与外筒限位台阶碰撞，活塞停止运动，内筒和滑杆组合体在惯性作用下继续向前运动，此时容腔内最大压力为9.2 MPa，容腔内压力已经开始降低；在1.34 ms时，内筒与滑杆组合体和弹射器本体分离，内筒和滑杆以一定速度飞出外筒，容腔内压力下降至9 MPa。从以上计算过程可以看出，整个计算模型完整反映了弹射器的弹射分离过程；当弹射器容腔较小时，容腔内火药燃烧产生的压力均一性较好；随着容腔的增大，容腔内燃气压力有一定梯度分布，最大压强与最小压强相差2 MPa左右，且火药位置的压强高于活塞尾部压强。

(a) 0.17 ms

(b) 0.62 ms

(c) 1.29 ms

(d) 1.34 ms图8 弹射器运动过程图Fig.8 The movement process of catapult at different moments

弹射器工作的主要性能指标为弹射速度，因此，通过弹射速度可以验证计算准确性。计算过程内筒速度曲线如图9所示。由图9中可知，内筒速度呈阶梯状增加，在0.6 ms时，活塞和滑杆组合体与内筒碰撞，将内筒速度迅速增加到17 m/s左右；此后，内筒速度出现一个平台，通过运动过程分析表明，这是由于碰撞后滑杆和活塞组合体速度降低，而内筒速度提高，导致滑杆和活塞组合体与内筒出现短暂分离；在0.9 ms左右，活塞和滑杆组合体在燃气压力作用下，再次与内筒发生碰撞，内筒速度进一步提高至25 m/s左右，然后又进入速度恒定段，组合体与内筒再次分离；依次循环，经过4次碰撞后，活塞被限位在外筒内，滑杆无法继续加速内筒，最终内筒和滑杆的组合体以35 m/s左右的速度飞出外筒。

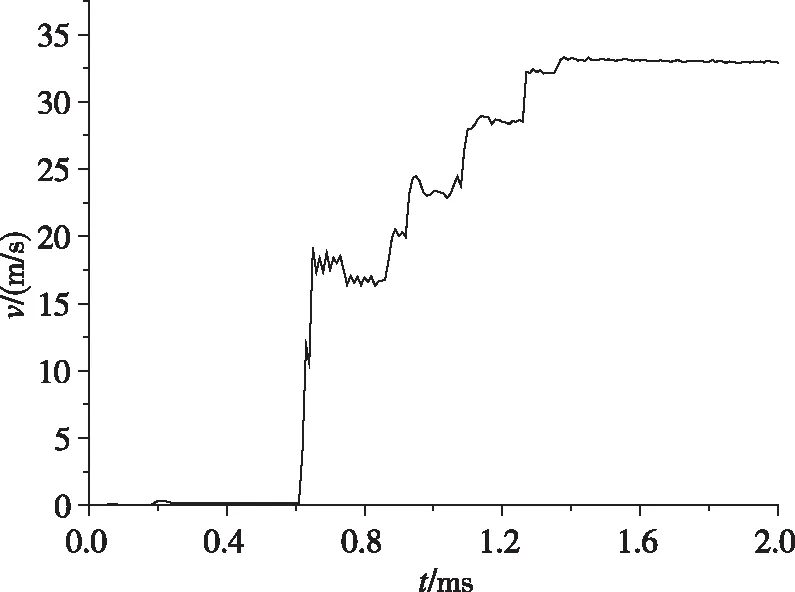
图9 计算过程内筒速度曲线Fig.9 Calculation velocity-time curve

试验测量内筒速度曲线如图10所示。由图10可知，试验测量的曲线相对平滑，这是由于测量设备采样频率仅有4 000 Hz，而内筒由开始运动到最大速度只有1 ms左右，因此，该试验测量并不能反映内筒加速过程的细节。最终，内筒达到的最大速度在40 m/s左右，而计算得到的最大速度在35 m/s左右，计算结果与试验结果误差在10%左右。考虑到计算模型对弹射器产品进行了较大简化，并且对点火器能量输出的描述有一定偏差，可以认为该计算结果与试验结果吻合性较好，因此火药燃烧模型和参数能够较好地描述弹射器工作过程。

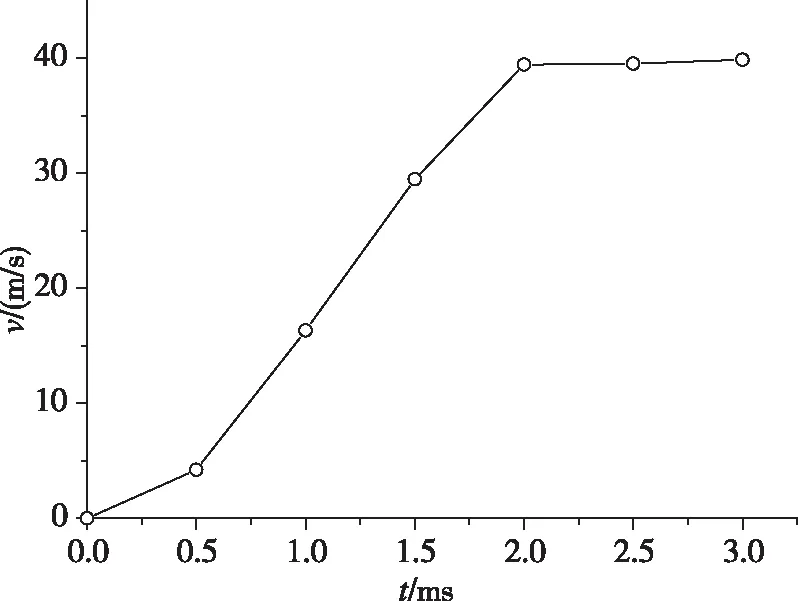
图10 试验测量内筒速度曲线Fig.10 Test velocity-time curve

5 结论

火药燃烧过程是一个复杂的物理化学过程，准确描述火药燃烧过程是进行火工装置工作过程数值模拟计算的关键。本文借鉴炸药反应的多项式模型，建立了火药燃烧单项式数学模型，模型由未反应状态方程、宏观燃速方程、微观反应速率方程和燃气状态方程组成；通过密闭爆发器试验数据拟合了SL17火药燃烧模型参数，并且对弹射器工作过程进行数值模拟计算，用以验证模型及参数的准确性。结果表明，密闭爆发器试验结果可以用于拟合火药燃烧模型参数；采用该模型和参数计算的弹射器运动过程可以完整反映弹射器弹射分离过程；计算得到的弹射分离速度与试验测量值吻合性较好，表明火药燃烧模型可以用于火工装置工作过程仿真计算。