某航天器火工装置作动后壳体滞后裂纹机理研究
叶耀坤, 丁 锋, 李晓刚, 穆慧娜
(1.北京空间飞行器总体设计部,北京 100094;2.北京理工大学,北京 100081)
0 引言
爆炸螺栓是航天器、卫星系统广泛应用的火工爆炸分离装置之一[1]。在某航天器的舱段分离系统中,使用了爆炸螺栓作为分离机构的核心作动部件,其主要由电点火器、管座、活塞、密封圈、壳体等零部件组成,如图1所示。
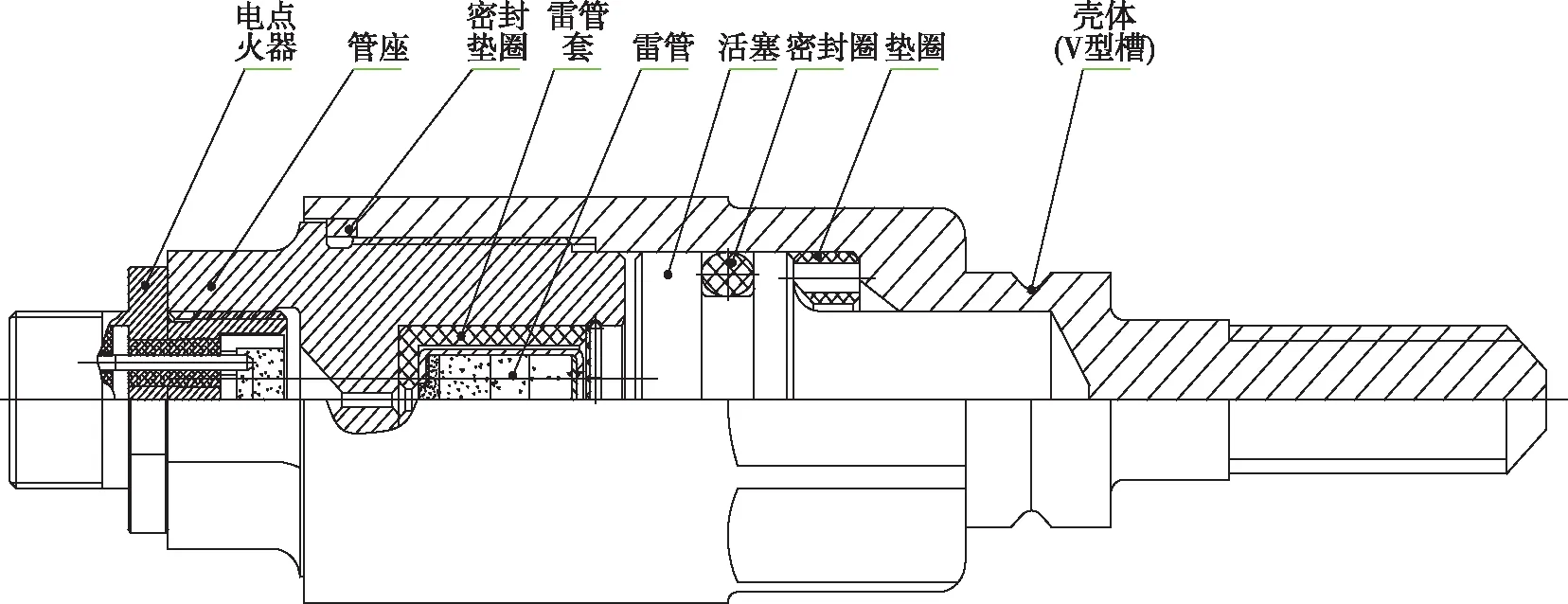
图1 爆炸螺栓结构组成图Fig.1 Explosion bolt structure composition
上述爆炸螺栓的工作原理为:连接时,其类似于螺钉通过壳体前端螺纹将分离结构连接在一起;分离时,依靠爆炸螺栓雷管装药的爆轰能量,推动活塞运动撞击壳体,并在爆炸螺栓壳体V形槽处将其撞断,从而实现解锁分离功能。
在上述爆炸螺栓研制试验过程中,进行了大、小药量和高低温条件下共计20发产品的验证试验。爆炸螺栓功能验证均正常,试验后检查残体并未发现壳体有异常现象,1 h后观察发现2发爆炸螺栓的壳体外圆柱面存在纵向裂纹,16 h后7发有裂纹,24 h后8发有裂纹,且部分产品的裂纹加大、增多。经统计分析,本次试验壳体出现滞后裂纹的产品比例为40%,均为高温发火下的大药量试验件。壳体裂纹的位置均靠近活塞停止运动部位,裂纹现象如图2所示。

图2 爆炸螺栓作动后的壳体滞后裂纹现象Fig.2 The hysteresis phenomenon of the shell after the explosion bolt actuated
上述现象表明爆炸螺栓存在一定缺陷,虽然均为完成解锁分离功能后出现,但考虑爆炸螺栓作用后其内部仍然存在高温高压燃气,如果壳体裂纹足够大,可能会造成安全隐患,对航天器的安全构型有不可估量的影响。为此,有必要针对该爆炸螺栓的壳体滞后裂纹机理开展研究,为后续的精准优化设计提供理论依据,减少试验耗费的成本。
为此,本文基于有限元模型的LS-DYNA数值仿真分析手段,分析爆炸螺栓密闭状态下的瞬态爆轰现象,获得产品作用过程中壳体或内部结构的应力分布情况,为揭示爆炸螺栓作用的壳体滞后开裂机理、优化螺栓壳体结构设计提供理论支撑。
1 有限元模型建立
1.1 LS-DYNA建模
爆炸螺栓主要由点火器、雷管、活塞、垫圈、壳体等组成,爆炸工作过程为:电点火器通电升温产生火焰,通过传火孔引燃雷管并输出爆轰波,活塞在爆轰波的冲击作用下开始加速并对螺栓壳体形成机械冲击,使壳体在预置V形槽处断裂,实现产品的解锁分离。将爆炸螺栓三维模型按照总—分—总的方式,先对总体模型做有限元模型简化,再分块建模,最后进行模型集成。该方法有两大优点:1)通过全局考虑,对于非关键做功步骤所牵涉的结构可以适当简化,然后进行模型分拆,便可多人多任务同时进行,有利于加快计算进度;2)建模过程由易到难,有利于寻找和控制各做功过程中影响数值计算的因素。在本研究中,先按零部件进行拆分,结合工作面切割方法,对各部分进行六面体为主、四面体为辅的网格划分,建立基本的有限元运算模型,有限元网格的尺寸为0.02~0.04 cm,网格总数量超过10万个,如图3所示。
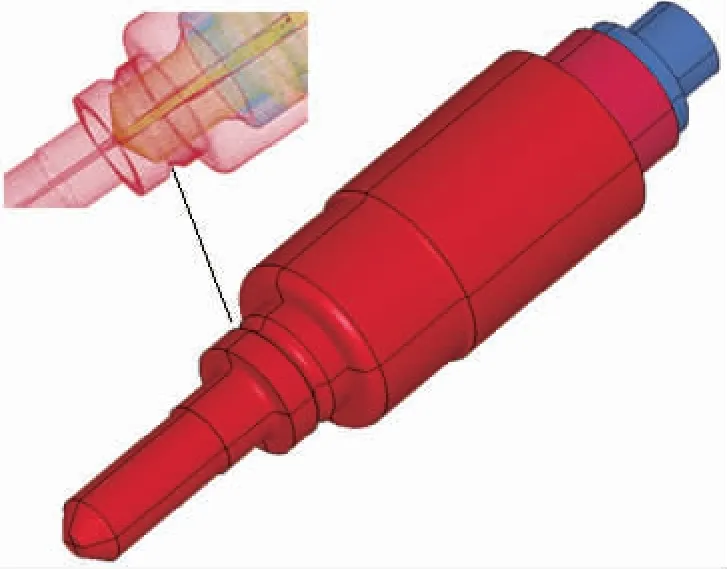
(a)全局模型

(b)1/4模型图3 爆炸螺栓数值仿真有限元模型Fig.3 Numerical simulation finite element model of the explosion bolt
爆炸螺栓的关键部件壳体、活塞的有限元模型如图4所示,通过多层次网格划分后,所获有限元单元主要以六面体为主,可有效提高仿真的效率和精度。

(a)壳体有限元模型

(b)活塞有限元模型图4 螺栓关键零件的有限元模型Fig.4 The finite element model of the key parts of the bolt
1.2 算法选择
本研究采用数值模拟软件ANSYS/LS-DYNA进行爆轰传递过程研究。使用该程序,用ANSYS建立模型,用LS-DYNA做显式求解,然后用标准的LS-PREPOST后处理来观看仿真分析结果。显式有限元程序LS-DYNA和ANSYS程序强大的前后处理在该软件中得到了有效结合。用LS-DYNA的显式算法能快速求解瞬时大变形动力学、大变形和多重非线性准静态问题以及复杂的接触碰撞问题,也可以在ANSYS和ANSYS-LS-DYNA之间传递几何信息和结果信息,便于执行连续的隐式-显式/显式-隐式分析。
LS-DYNA程序算法以拉格朗日(Lagrange)算法为主,兼有欧拉(Euler)和ALE(Abritrary Lagrangian Eulerian)算法。在有限元分析中,需根据模型的具体结构、应力应变产生的主要位置、材料的类型以及计算的精度要求进行算法的选择。所选算法的合理性将直接影响计算结果的准确度与可信度,同时还可能大幅度地改变运算周期。由于爆炸螺栓包含火工品单元,若采用Lagrange单元,其装药结构在数值模拟的过程中会产生大的形变,畸变的网格可能会减慢运算速度,甚至会导致计算终止[2]。因此,本研究对空气、填充物与雷管装药采用ALE多物质算法,壳体等其他结构采用Lagrange单元,并采用关键词*CONSTRAINED_LAGRANGE_IN_ SOLID_TITLE完成ALE与Lagrange网格的耦合。
1.3 材料模型与状态方程
LS-DYNA程序中有金属和非金属材料100余种可供选用,如弹性、弹塑性、超弹性、泡沫、玻璃、地质、混凝土、土壤、复合材料、炸药及起爆燃烧、刚性以及自定义材料[2],在本研究中,结合不同零部件的特征选用不同的材料模型,便于兼顾仿真分析的精度与效率。
(1)主要金属材料模型选取
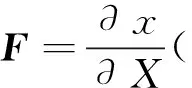
F=RU
(1)
式中,R=FU-1为正交旋转张量,U=(FTF)1/2为对称正定张量,称为右伸长向量。采用Green-Naghdi应力率
(2)
式中,ω=RRT为旋转率张量,σ为柯西应力。
各向同性硬化材料塑性加载时,屈服面中心固定不变而屈服面半径增大,随动硬化材料塑性加载时,屈服面半径不变而屈服中心沿塑性应变方向平移。对于大多数实际材料,屈服硬化规律介于各向同性与随动硬化之间,称为混合硬化模式[2]。
由于爆炸螺栓的壳体、活塞、管座、点火器壳体是开裂现象的关键零部件,其材料均为30CrMnSiNi2A,并均进行了除氢处理。为了保证仿真分析的精度,其材料模型选用弹塑性混合硬化模式。有限元计算采用cm-g-μs单位制,导出单位:压力107N,应力/压力Mbar,速度10 km/s,密度103kg/m3。仿真分析过程中主要金属零部件的材料参数见表1。

表1 主要金属零部件的材料参数Tab.1 Material parameters of main metal parts
(2)流固耦合模型中的空气域材料模型
在爆炸螺栓仿真分析模型中,建立了流固耦合模型,其中空气域选用空白材料模型,可避免炸药爆轰过程计算应力、应变[3]。
(3)爆炸螺栓装药材料模型与状态方程
爆炸螺栓的点火器装药为镁粉点火药,雷管主装药为斯蒂芬酸铅(150 mg)、叠氮化铅(220 mg)、太安(310 mg)3种药剂,其中太安作为主装药。通过火炸药材料手册可以获得上述3种药剂的爆速分别为3.8,4.7 ,7.2 km/s[4]。
在爆炸螺栓仿真分析模型中,所有药剂均采用高能炸药燃烧材料模型,输入参数:爆速D,C-J压力Pc-j与燃烧系数
Ff=max(Ff1、Ff2)
(3)

式中,te为爆轰波由起点传至当前单元中心处所需最短时间。若Ff>1,则取Ff=1。
此外,在爆炸螺栓装药序列的数值模型中,主发装药均采用*MAT_HIGH_EXPLOSIVE_BURN模型和JWL状态方程,被激发药采用LS-DYNA程序中为反应速率提供的Lee-Tarver点火与增长反应率模型。其中JWL状态方程是凝聚炸药典型的动力学状态方程,它能描述火炸药爆轰产物压力—比容—比内能(P-V-E)关系[5]。方程形式为
(4)

点火与增长状态方程:此模型假设少量炸药由于冲击波加热而被点火,形成微小球形燃烧区。其反应率由压力及表面积所控制。微小球形燃烧区的增长,使热点间的炸药在10-6s内耗尽。基于上述假设的反应率方程可写为
G1(1-λ)cλdpy+G2(1-λ)eλgpz
(5)
式(5)中右边第一项代表点火项,参数a是临界压缩度,在一定的压缩度情况下才允许点火。在点火项和第一增长项中的(1-λ)参数b和c等于2/3,代表向内的球形颗粒燃烧。点火量作为冲击强度和持续时间的函数,其大小由参数I和x控制。G1和d控制点火后的早期增长,G2和z确定高压反应速率[6]。各项参数取值如表2所示。
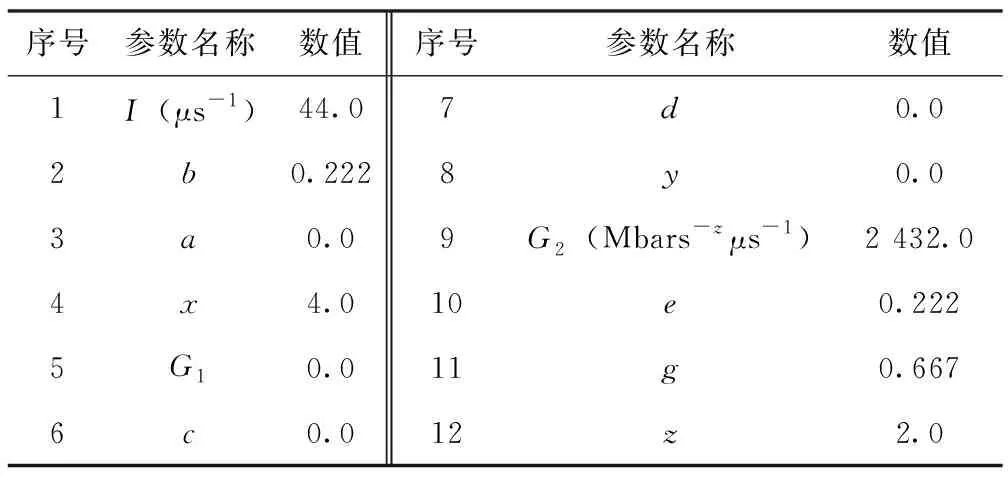
表2 点火—增长反应速率方程主要参数Tab.2 Ignition-growth reaction rate equation main parameters
2 爆炸螺栓作用过程机理分析
爆炸螺栓的作用过程大致可以分为3个阶段[7]:1)点火器通过管座的传火孔起爆雷管;2)爆轰波在雷管装药内部传爆并加载于活塞端面;3)活塞在冲击波作用下向前撞击螺栓壳体,致使螺栓壳体在预置V形槽处断开并实现分离。
由于爆炸螺栓流固耦合模型计算复杂,仿真分析过程中需采用先局部后总体的运算模式,通过局部计算,调整模型网格的各项指标,消除网格畸变、死循环等困扰,然后进行系统模型的总体计算,实现爆炸螺栓做功全过程的仿真分析。
首先,电点火器产生的火焰通过点火孔引燃雷管,使得雷管内的装药产生强爆轰输出。相对而言,火焰的冲击强度要小得多,且通过点火孔衰减,对雷管处燃腔产生的冲击作用很小,因此,可弱化电点火器的功能作用,对其结构进行适当简化,采用等能量的高能炸药替代,利用点火—增长模型进行该过程的数值模拟[8]。点火器引燃后的压力云图分析结果如图5所示。

图5 点火器作用后的压力云图Fig.5 Pressure cloud map after the igniter acts
点火器引燃后,药剂的化学反应持续进行并对外输出能量,通过管座中的传火孔起爆雷管组件中的斯蒂芬酸铅,该历程可由图6进行表征。
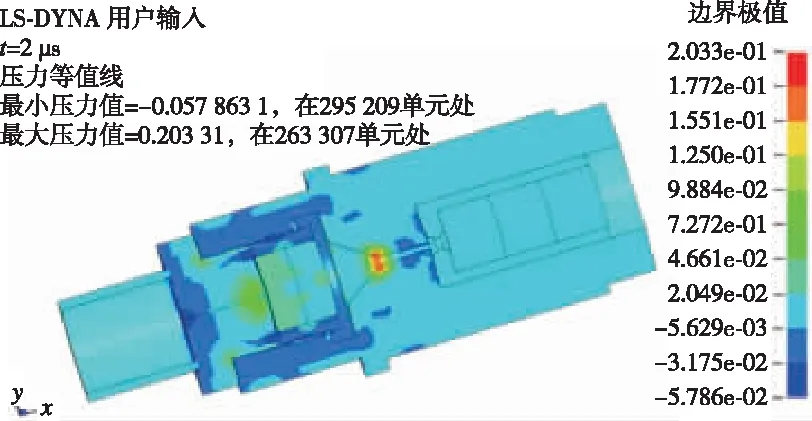
图6 点火器传火与起爆雷管第一层装药的压力云图Fig.6 Pressure cloud map of the first layer of charge of the igniter and detonator growth process
雷管的第一层装药被引爆后,爆轰波逐步成长并趋于稳定后形成对下级装药的冲击起爆,雷管成长过程的压力云图如图7所示。
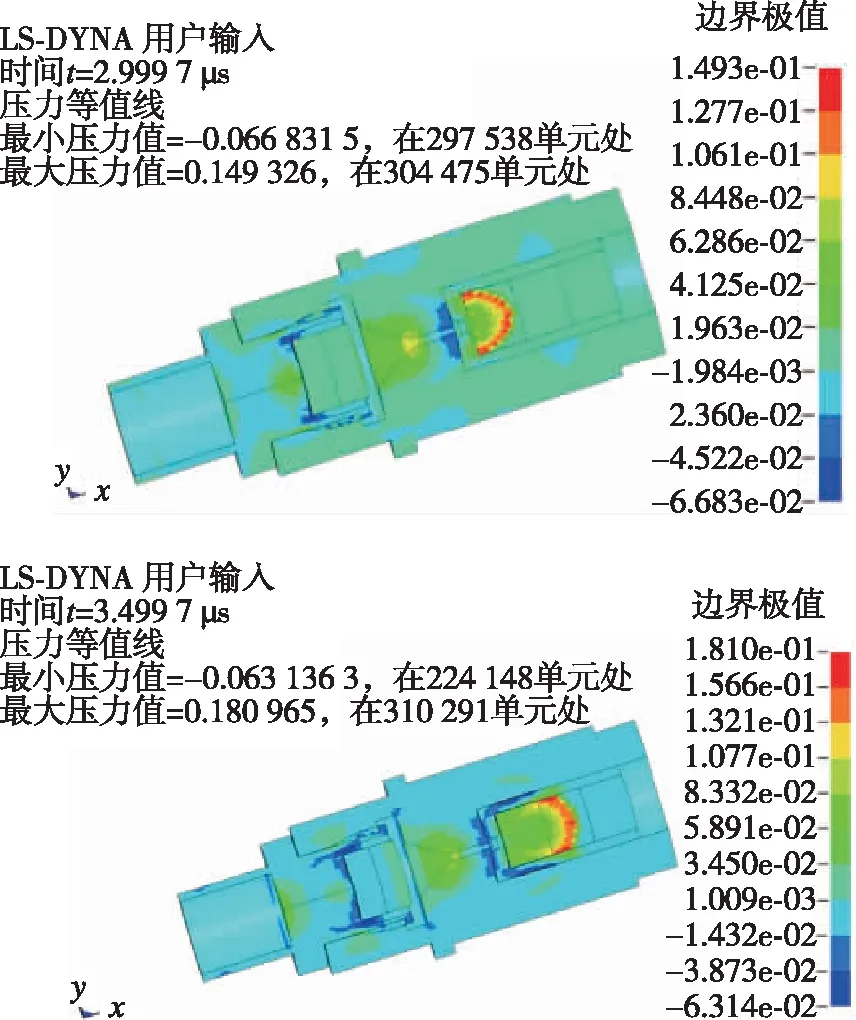
图7 雷管第一层、第二层装药爆轰成长过程的压力云图Fig.7 Pressure cloud map of the first layer and second layer of charge initiation process
爆炸螺栓点火与雷管起爆过程还可以通过雷管装药的压力进行表征,在雷管的三级装药中,沿中轴线自上而下选取若干个有限元,绘制其压力曲线,如图8所示。

图8 雷管第一层、第二层装药爆炸压力增长过程曲线Fig.8 Pressure curve of the first layer and second layer of charge initiation process
上述结果表明,经历了约2 μs后,雷管靠近点火器的端面上开始出现压力,说明点火器成功作用并开始起爆雷管,随着时间推移,雷管装药上的压力峰值不断增大,至3.3 μs时达到最大,随后压力突然下降,表明第一级装药完全消耗。随后,又出现一波逐步上升的压力峰,表明下级装药被成功起爆并实现了能量的传递。各个有限元单元上的压力值都具有相似的变化规律,先迅速上升然后快速下降,随后出现一个震荡的次级峰,其中第一个峰表示冲击波快速通过时加载的压力,后一个震荡峰则是波后质子在腔体内形成的冲击与压力。
雷管中的叠氮化铅被斯蒂芬酸铅起爆后,输出压力继续起爆主装药太安,输出压力在雷管壳输出端盖片、空气等介质中衰减后加载在活塞上,爆轰波传递过程如图9所示。
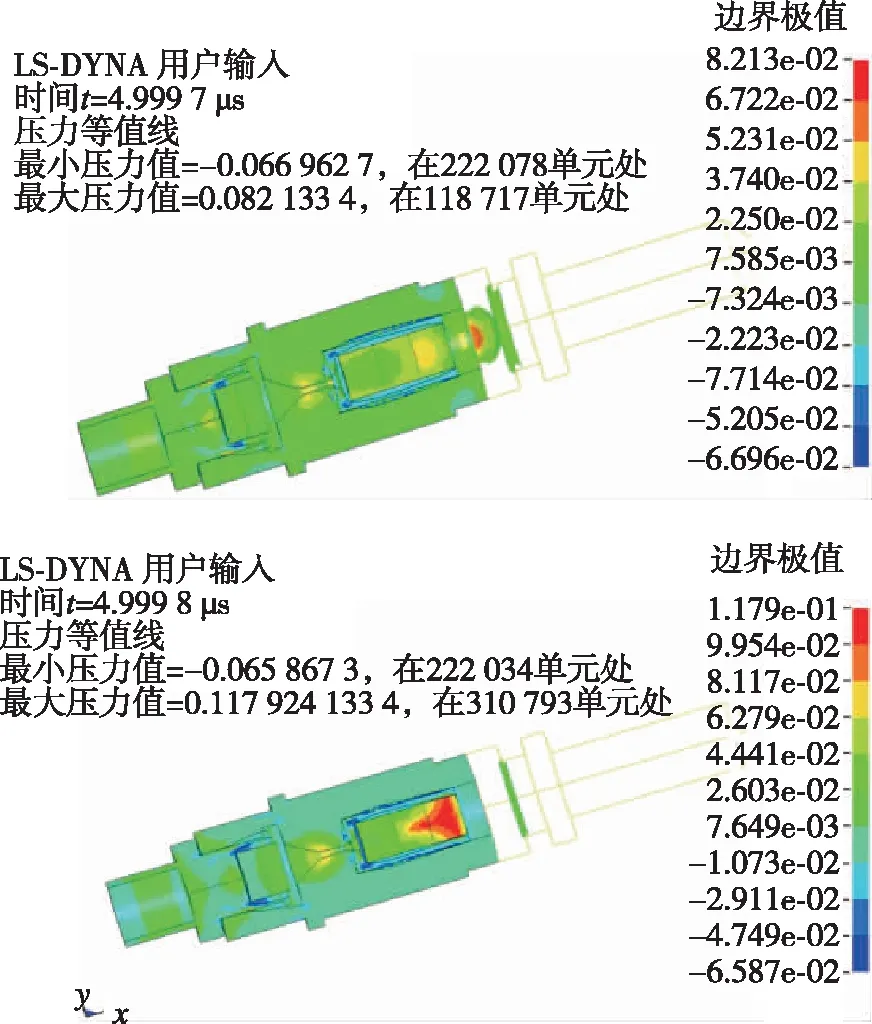
图9 主装药太安起爆过程压力云图Fig.9 Pressure cloud map of main charge Tai-an initiation process
点火器开始作用约3 μs后,雷管被引爆,约5 μs后雷管的三级装药均作用完毕,爆轰波到达活塞端面,活塞在冲击波的作用下向前推进,并高速撞击螺栓壳体,壳体发生拉伸作用。48 μs左右,预制V形沟槽处开始出现颈缩,随后开始出现环形裂纹,并于86 μs左右完全断裂,爆炸螺栓被一分为二,实现了解锁分离功能,如图10所示。
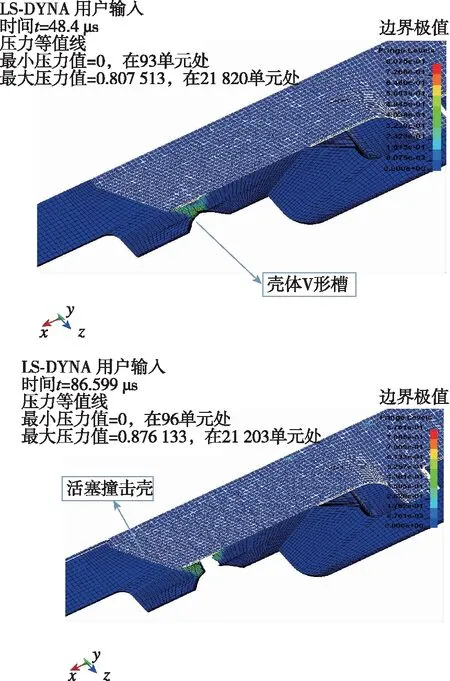
图10 爆炸螺栓壳体V形槽断裂过程仿真结果Fig.10 Simulation result of shell-shaped fracture process of explosion bolt
上述爆炸螺栓的作用全过程仿真分析表明,爆炸螺栓的现有设计可以满足解锁分离功能要求,同时有效揭示了爆炸螺栓的内部作用过程,可解决作用过程不可测难题,同时也为爆炸螺栓的壳体滞后开裂研究建立了可行的研究手段。
3 壳体滞后裂纹机理分析
采用第2章中的训练模型进行数值仿真,获得爆炸螺栓的壳体依次在2.599,5.599,15.99 μs等不同时刻的应力云图,如图11所示。

图11 爆炸螺栓的壳体应力云图Fig.11 Shell stress cloud diagram of explosion bolt
针对螺栓壳体受冲击程度的不同,可将主要受压区域按不同的壁厚分为a,b,c3段,其对应的壁厚值依次为2.75,3.75,3 mm,此外a段与管座壳体重合,c段与活塞重合,b段部分处于空白域,如图12所示。
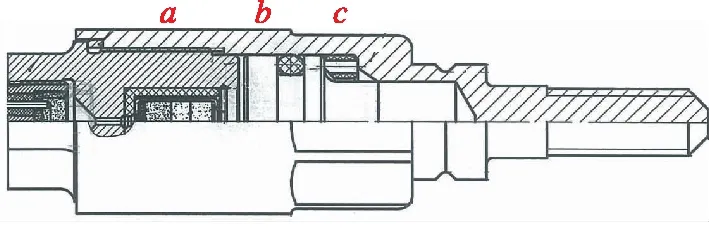
图12 爆炸螺栓的壳体壁厚分段Fig.12 Shell wall thickness section of the explosion bolt
从仿真分析结果中提取壳体不同段的有限元单元应力曲线,如图13所示。
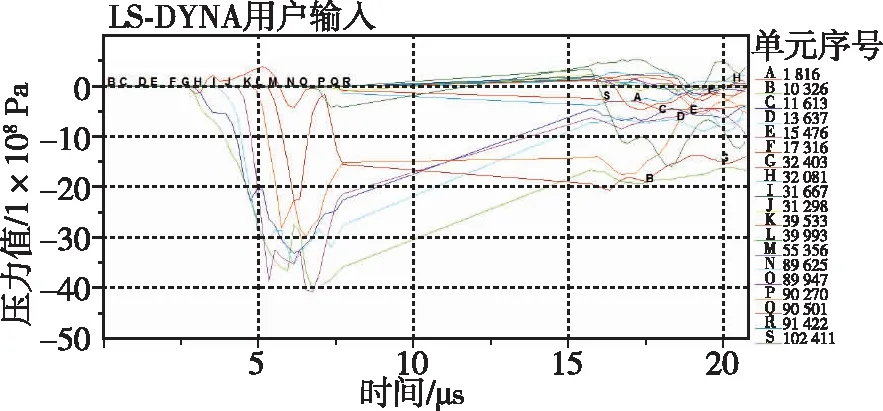
图13 爆炸螺栓壳体应力曲线Fig.13 Stress curve of explosion bolt shell
图13曲线表明,壳体腔内的应力峰值在3 000~4 000 MPa之间,应力较大区域为b段空白区域,原因是雷管爆炸后爆轰波直接作用于壳体内壁,使之往外膨胀,所受冲击较强,因而产生的应力也较大。
借鉴薄壁筒应力计算方法,壳体理论可承受的应力按以下公式进行估算
σ=(πD2/4-πd2/4)σb
(6)
式中,D和d分别表示壳体圆筒的内外径,σb表示螺栓壳体热处理后的强度,此处按照实际热处理强度值取1 390 MPa。
依据式(6)可以计算出各段的拉伸应力,结果如表3所示。

表3 爆炸螺栓壳体应力计算结果Tab.3 Calculation results of shell stress of explosion bolts
从表中数据可以看出,除a段应力2 972 MPa小于3 000 MPa以外,b,c两段的拉伸应力均大于或正处于仿真计算的结果范围内,因此b,c两段通常不会率先开裂或失效。对于a段单从计算结果与仿真计算的结果来看,在强冲击过后应该会出现裂纹或失效,但螺栓壳体的a段处于管座的外围,管座的壁厚约5 mm,所能承载的拉伸或剪切力为4 200 MPa左右,两者相加为7 172 MPa,远远高于仿真结果应力值,因而不会产生裂纹失效。c段由于活塞与壳体存在重合段,可以避免直接的爆炸冲击损伤。理论上,爆炸螺栓壳体可以承受4 000 MPa应力,最薄弱环节为壳体的b段,略小于实际应力水平,存在强度临界状态。
然而,比较爆炸螺栓壳体的外径与厚度,也可将其视为厚壁筒,对于受内压作用的厚壁筒,塑性区由内壁开始向外扩展,形式为内层为塑性区,外层为弹性区。由于外层弹性区的约束,内层塑性区的变形仍与弹性变形为同一量级,一旦全截面均进入塑性状态,无限制的塑性流动便成为可能。因此,如果爆炸螺栓在作用过程中未达到全截面塑性状态,而内部塑性区厚度较大,在存放过程中由于壳体容腔内的爆炸压力、温度等环境条件逐步变化,引起壳体的内部应力水平缓慢发生波动变化,并随着壳体温度应力的完全释放以及内部爆炸压力的缓慢卸载,导致塑性区域的加大,从而出现裂纹,最终壳体应力水平达到均匀平衡状态。
此外,从材料疲劳裂纹的萌生与扩展机理可知,金属材料疲劳裂纹起源于应变集中的局部显微区域,即所谓疲劳源区,如图14所示,爆炸螺栓在完成做功后,壳体的内壁出现了几个应变集中局部显微区域,主要分布在a,b,c段的交界处。

图14 爆炸螺栓壳体的应力应变集中区域Fig.14 Stress and strain concentration area of explosion bolt shell
疲劳条纹的形成过程可以用Laird模型来说明,当交变应力为零时,循环开始时裂纹处于闭合状态,拉应力增大后,裂纹张开,且顶端沿最大切应力方向产生滑移,当应力继续增大至最大值,裂纹张开最大,相应的塑性变形范围也随之扩大[9]。由于塑性变形,裂纹顶端钝化,应力集中减少,当应力反向时,滑移方向也改变,裂纹表面被压拢。到压应力最大时,裂纹完全闭合,并恢复到这一周次的开始状态,但裂纹却扩展了一个相当裂纹扩展速率数值的增量。爆炸螺栓在完成做功后,相当长一段时间内都处于如图15所示的交变应力震荡状态下,且随着时间推移,壳体内部爆热、爆压下降导致壳体发生缩变,其中爆热下降持续约2 h后趋于平衡,爆压下降持续约30 h后趋于平衡,在两者综合作用下,使得壳体b段的滞后开裂成为可能,这也与爆炸螺栓试验过程b段出现滞后裂纹现象吻合。

图15 螺栓壳体受力情况Fig.15 Stress condition of bolt shell
结合上述机理,为有效解决爆炸螺栓的壳体b段滞后开裂问题,一方面可以通过减少主装药量,降低爆炸产生的应力水平;另一方面可以通过增加壳体b段的壁厚,提升壳体承受的极限应力能力[10]。
4 结论
本文针对某航天器爆炸螺栓发火试验后出现壳体滞后裂纹问题,采用了LS-DYNA有限元仿真手段,建立了爆炸螺栓作用全过程仿真模型,完整地模拟了爆炸螺栓从点火到输出的全动态作用过程,得到了爆炸螺栓作用过程中各阶段作动时序以及结构应力分布,揭示了壳体薄弱段的滞后裂纹机理,并提出了优化改进措施,为工程研制提供了理论支撑。

