基于杂交粒子群的认知无线电网络功率分配算法
赵 璐,周明月
(长春工业大学 计算机科学与工程学院, 吉林 长春 130102)
0 引 言
近些年,全球无线通信事业蓬勃发展,人类在虚拟世界的探索更加深入,开始不得不面对发展的一大瓶颈,如何公平合理地分配利用无线频谱资源。无线频谱资源属于十分宝贵的不可再生资源,然而长期以来都是通过静态频谱分配方式管理频谱资源,导致很多无线频谱资源经常处于闲置状态,由于频谱使用权限问题,其他无权限用户无法使用这些闲置无线频谱资源,造成了无线频谱资源的极大浪费。因此,认知无线电技术(Cognitive Radio, CR)受到越来越多学者的重视,其主要思想是在不影响现有通信系统的情况下,对于空闲的频谱资源再利用,这种方法是目前较为流行的频谱资源再利用方法。
在认知无线电网络模型中,将用户分为主用户(Primary users, PUs)和次用户(Second users, SUs)。CR系统允许SUs满足对PUs的干扰小于干扰阈值的条件下进行通信,这种同时进行的通信方式称为共存式频谱共享方式(Underlay),另外一种接入方式SUs用户在PUs用户不通信时接入使用频谱资源,这种伺机接入方式称为机会式频谱共享(Overlay)。然而在特殊情况下,SUs不能停止通信,因此,文中主要研究共存式频谱共享方式。
在认知无线电模型中,通过合理的功率分配算法,使SUs用户满足各种约束条件下达到总的信道容量最大或总的功率最小。但当某个SUs用户的发射功率越大时,它对其他的SUs用户和PUs用户造成的干扰就会越大,在很多模型中,研究者只考虑到最大信道容量或最小功率,往往没有考虑到各个SUs用户之间的公平性问题,这样的模型在实际中并不是很理想。
文献[1]提出一种基于公平度门限的认知无线电资源分配算法,在OFDM系统中通过Jain公平性指数(公平性指数用来衡量用户间获取资源是否公平的实数)约束提高公平度。文献[2]提出一种改进粒子群算法,提高了次用户的信道容量。文献[3]提出一种基于遗传粒子群算法的认知无线电系统功率分配算法,提高次用户的信干噪比,降低发射功率。文献[4]研究了Underlay模式下认知无线电网络资源动态分配问题,从不同角度解决认知无线电资源问题。
文中以主用户干扰约束和次用户自身发射功率约束,以及次用户信道容量方差阈值约束作为前提条件,提出一种增加用户公平性的低复杂度算法,该算法不仅收敛速度快,而且最大化信道容量。仿真实验验证该算法的可行性。
1 系统模型和问题规划
1.1 系统模型
认知无线电系统模型如图1所示。

图1 认知无线电系统模型
在一对主用户发射机(PU-TX)和接收机(PU-RX),以及m对次用户发射机(SU-TX)和接收机(SU-RX)的系统中,分配SU-TX的发射功率,实现最大化信道容量。
首先要求各SUs对于PU的干扰功率总和不能超过PU所能承受的干扰功率阈值为

(1)
式中:hi----次用户对于主用户的干扰增益;
pi----次用户的发射功率;
I----主用户所能承受的干扰功率阈值。
各次用户的发射功率必须小于最大允许发射功率,
pi≤pmax,
(2)
式中:pmax----SUs的最大发射功率。
为了提高次用户之间的公平性,以各次用户信道容量方差作为约束条件,这样不仅提高了系统的公平性,还使得算法较比例化信道容量算法更加简单灵活,信道容量方差约束为
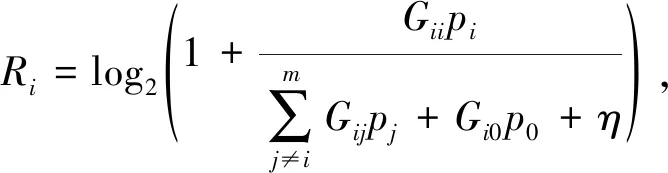
(3)
式中:Ri----次用户各自的信道容量;
Gii----次用户发射机i到次用户接收机i的信道增益;
Gij----次用户发射机j到次用户接收机i的信道增益;
Gi0----主用户发射机到次用户接收机i的信道增益;
p0----主用户发射功率;
η----系统的背景噪声。

(4)
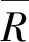

(5)
式中:Dx----信道容量方差阈值。
我们的目标是最大化信道容量,结合上述几条约束,数学模型表达式为

(6)
1.2 功率分配
根据以上优化模型,此模型是一个非线性且非凸优化问题,其中考虑到公平性问题,若使用传统寻优算法,如拉格朗日乘子法,则计算复杂度较高,并且收敛速度会很慢,因此,文中采用粒子群智能优化算法进行求解。
1.2.1 基本粒子群算法
粒子群算法(PSO)是一种简单高效的智能优化算法,1995年由两位美国学者提出,相较于传统算法,此算法计算速度快,全局寻优能力很强;该算法适用于连续函数极值问题,对于多峰值、非线性问题都有较强的全局搜索能力。
粒子群粒子飞行迭代图如图2所示。
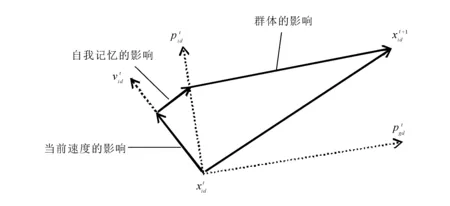
图2 粒子群粒子飞行迭代图
图中:x----粒子起始位置;
v----粒子飞行速度;
p----搜索粒子的最优位置;
i----第i个粒子;
d----维度;
t----迭代次数。
开始阶段,粒子群算法会生成一群随机粒子(随机解),然后通过迭代找到最优解。在每次迭代中,各个粒子通过追寻两个极值来更新自己;一个是粒子本身找到的最优解个体极值pbest;另一个是整个种群目前找到的最优解全局极值gbest。
粒子i在t时刻第d维度根据下式更新自己的速度和位置:
vid=w*vid+c1r1(pid-xid)+
c2r2(pgd-xid),
(7)
xid=xid+vid,
(8)
式中:c1,c2----学习因子,也称为加速常数;
w----惯性权重;
r1,r2----[0,1]范围内的均匀随机数。
式(7)等号右边由三部分组成:第一部分是粒子当前的惯性权重影响的速度,代表粒子有维持自己先前速度的惯性;第二部分为认知部分,它表示粒子对自身飞行经验的记忆或回忆,代表粒子根据自身历史修改飞行方向,可以更好地辅助粒子跳出局部最优;第三部分为群体部分,粒子为了向群体最优位置飞行,进行合作将它们的信息相互分享,帮助群体调整飞行方向。
1.2.2 对于不满足约束条件的粒子处理
在有约束的粒子群算法中,对粒子是否满足约束进行判断,如果当前粒子位置满足各项约束条件,那么对它的当前适应度值加上零;如果不满足约束条件,那么对它的当前适应度值加上一个非常大的值(若所求适应度值是个最小值时)或一个非常小的值(若所求适应度值是个最大值时)。这样不满足约束条件的当前粒子位置就会由于极差的适应度值被淘汰,具体表达式为

(9)

(10)

(11)
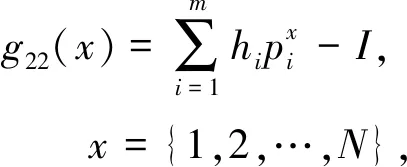
(12)

(13)
式中:f(x)----x粒子当前的适应度;

F(x)----x粒子进行约束判断后的适应度。
式(11)~式(13)是约束判别式,由三条约束条件得出,通过它们可以判断粒子是否满足约束条件。
1.2.3 基于杂交粒子群算法
杂交粒子群算法参考了遗传算法中的杂交理念,可以提高粒子的全局搜索能力,增强收敛速度和收敛精度。就是在算法每次迭代中,按照杂交率抽取相应数量的粒子放入杂交池内,将池内的粒子随机两两杂交后,产生相等数量的子代粒子,然后用子代粒子代替父代粒子[8]。子代位置速度表达式为:
sx=i*fx(1)+(1-i)*fx(2),
(14)

(15)
式中:sx----子代位置;
sv----子代速度;
fx----父代位置;
fv----父代速度;
i----0到1之间的随机数。
具体算法步骤如下:
1)初始化种群,随机生成初始种群位置,并随机生成初始种群速度;
2)初始化个体历史最佳位置,以及个体历史最佳适应度;初始化群体历史最佳位置,以及群体历史最佳适应度;
3)根据式(7)更新粒子速度,并进行边界处理,根据式(8)更新粒子位置,并进行边界处理;
4)进行约束条件判定,并重新计算新种群每个个体位置的适应度;
5)将每个粒子的新适应度与个体历史最佳适应度进行比较,将个体历史最佳适应度与种群历史最佳适应度做比较,并更新全局极值;
6)抽取指定数量的粒子根据杂交概率,然后放入杂交池中,池中的粒子随机两两杂交产生同样数目的子代粒子,子代粒子的位置和速度由式(14)和式(15)求得,并保持个体极值和全局极值不变;
7)如果算法触发终止迭代条件时,会马上结束搜索,然后输出结果;如果没有触发终止迭代条件,则返回到3)继续搜索。
2 仿真结果与分析
通过计算机仿真实验验证所提出算法的性能。网络仿真环境是在Matlab R2016a搭建的[9]。所有仿真参数设置如下:系统中有1个主用户和3个次用户,主用户允许的干扰功率阈值为1 mW,各次用户的信道容量方差约束设为0.1。种群规模设置为100,粒子维度设置为3,最大迭代次数设置为30次。将普通粒子群算法和基于杂交的粒子群算法作比较。
次用户总的信道容量收敛过程如图3所示。
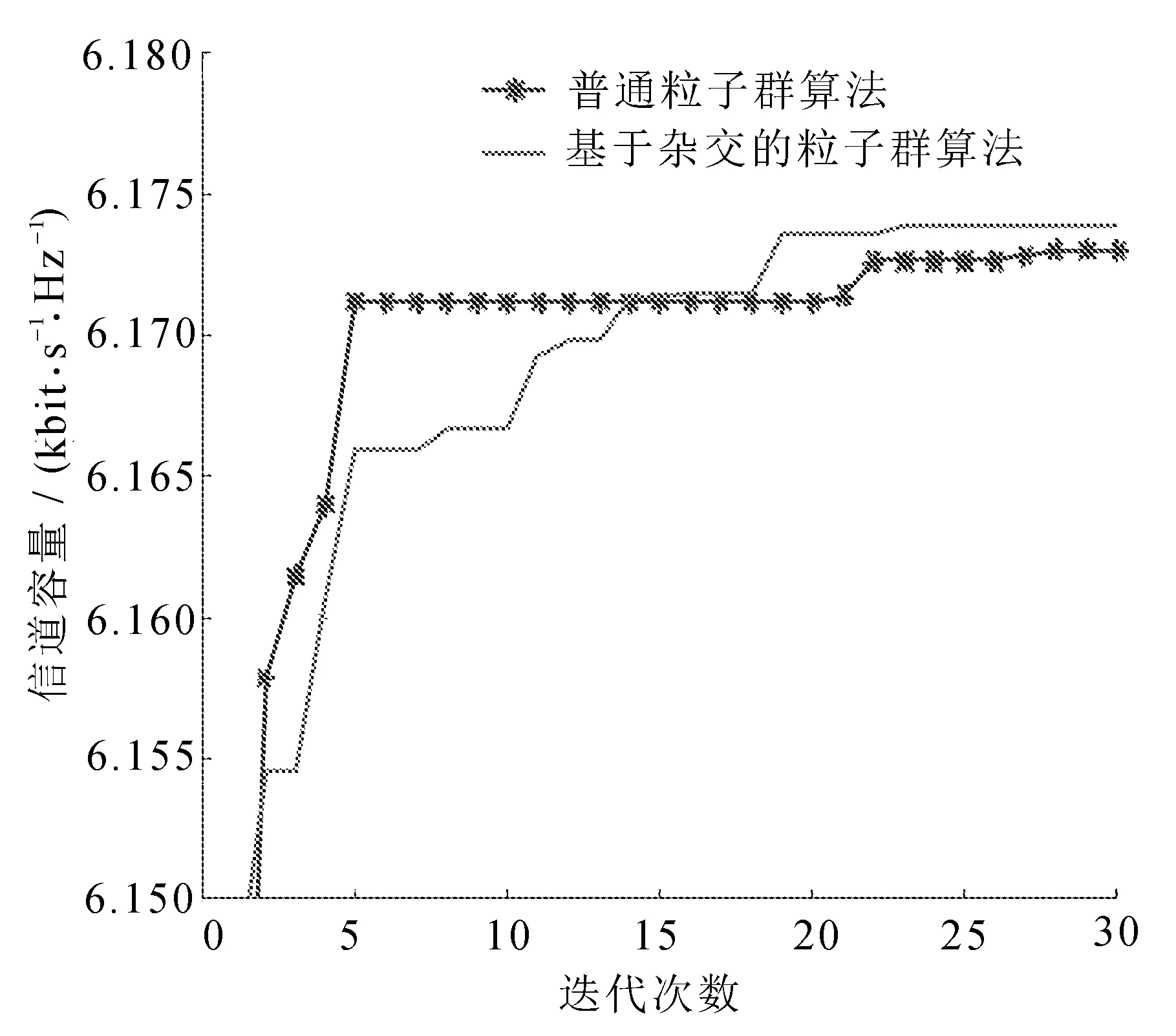
图3 次用户总的信道容量收敛过程
在相同的约束条件下,相同的粒子种群数量以及迭代次数情况下,普通粒子群和杂交粒子群算法都可以得出收敛结果,显然基于杂交的粒子群算法较普通粒子群算法收敛速度更快,寻优效果更好。
基于杂交PSO算法的次用户信道容量如图4所示。

图4 基于杂交PSO算法次用户信道容量
从图4可以看出,3个次用户的信道容量收敛位置很接近,在迭代到20次左右,甚至3个用户的信道容量重叠在一起,但最后并没有收敛于此,说明此处的信道容量方差虽然很小,但不是约束条件下的最大信道容量位置,因此粒子飞向其他更佳位置。此算法在满足次用户信道容量方差阈值的约束条件下,实现信道容量最大化。
基于杂交PSO算法次用户的功率收敛过程如图5所示。

图5 基于杂交PSO算法次用户的功率收敛过程
从图5可以看出,3个次用户的功率收敛位置非常接近,说明此算法的公平性非常好。当一个次用户的功率很大时,会对其他次用户造成很大干扰,如果只是追求最大信道容量时,只需使信道环境最好的次用户功率最大,其他次用户功率设置为零(在满足约束条件下),但为了保证一定的用户公平性,要做出调整,牺牲一些信道容量。
各个次用户基于杂交PSO功率分配算法的SINR如图6所示。

图6 基于杂交PSO次用户的SINR
显然,各次用户的SINR很接近,且SINR还很高,说明此算法不仅保证了公平性,还保证了通信质量。
基于杂交PSO次用户对主用户的干扰功率如图7所示。

图7 基于杂交PSO次用户对主用户的干扰功率
显然,粒子的收敛位置刚好等于1 mW,不超过主用户干扰功率最大值,满足约束条件的同时,还能最大化利用信道资源,说明此算法精度很高。
3 结 语
在Underlay认知无线电网络中,提出一种基于杂交粒子群算法功率分配算法,仿真结果表明,此算法比普通粒子群算法收敛速度快,寻优效果好,实现了模型中次用户之间的公平性,并且将信道资源在约束条件下最大化利用。

