混合函数型数据下Logistic回归模型的惩罚估计
袁晓惠,金宛霖,曹儒雅
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
函数型数据最早由Ramsay J O[1]提出,常以曲线或者图像形式出现。由于其无限维的特性,传统的数据处理方法具有局限性,需要探索新的方法和模型对函数型数据进行分析,其中最经典的是函数型线性回归模型。Ramsay J O等[2]使用函数型线性模型对加拿大的温度和降雨量进行了实证分析。刘锋等[3]利用低阶基函数的线性组合研究了函数型线性模型在肉类光谱数据上的应用。Lin Z等[4]提出一种称为“fSCAD”(functional SCAD)的方法。基于B-样条,结合粗糙度惩罚和稀疏惩罚得到回归参数的最小二乘估计。徐梦佳[5]构造带惩罚项的函数型多元线性回归模型,并将该模型应用到江西省的空气质量分析中。
对于协变量是函数,响应变量是二值标量的情形,经典的统计模型为函数型Logistic回归模型。Cardot H等[6]分析了标量响应和函数预测之间的联系,在光滑性假设的条件下,利用样条逼近的惩罚似然来估计模型中的系数函数。Liu Y等[7]提出一种稀疏的函数型Logistic模型来预测抑郁症患者的治疗缓解状态,并将函数型数据分析应用在重度抑郁这样的疾病研究。王惠文等[8]研究含有函数型协变量的Logistic模型,结合B-样条基函数,得到该模型回归参数的极大似然估计。
对于响应变量是标量,协变量是混合函数型数据的情形,最常见统计的模型是部分函数型线性模型。程丽娟[9]对部分函数型线性模型在上证指数中的应用进行了研究。张雪[10]采用预平滑的方法得到部分函数型线性模型中系数函数的估计。丁辉[11]研究了部分函数型线性模型的局部稀疏估计,采用最小二乘法,结合粗糙度惩罚和fSCAD方法分别估计函数型系数和标量型系数。
梳理文献发现,尽管已有文献给出了各种函数型回归模型的研究和应用,但对协变量同时包含函数型数据和数值型数据的Logistic模型研究还很少。文中针对响应变量为二分类[12-13],协变量为混合函数型数据的情形,构造Logistic回归模型,并求得回归参数的惩罚似然估计,最后将该模型应用于实例数据中。
1 函数型Logistic回归模型介绍
数据类型为{Yi,Xi(t),Zi},i=1,2,…,n,响应变量Yi∈{0,1},协变量为混合函数型数据的Logistic回归模型为
P(Yi=1|Xi(t),Zi)=
(1)
i=1,2,…,n,
式中:μ----截距项;
β(t)----系数函数;
X1(t),X2(t),…,Xn(t)----定义在区间[0,T]上的函数型协变量;
Zi----p维向量,Zi=(Zi1,Zi2,…,Zip)T;
α----Zi的系数,α=(α1,α2,…,αp)T。
以Logit为链接函数,则式(1)可表示为
logitP(Yi=1|Xi(t),Zi)=
i=1,2,…,n。
该模型描述了标量型响应变量和混合型协变量之间的关系,根据式(1)求得该模型的对数似然函数为
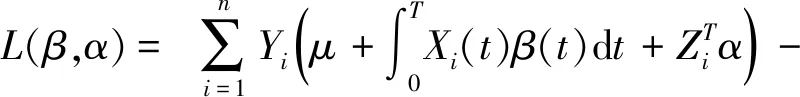
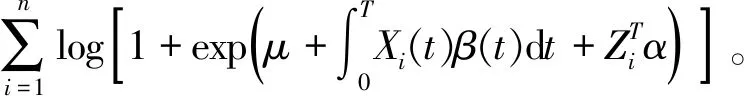
(2)
2 函数型Logistic回归模型的惩罚似然估计
由于函数型数据是一种新型高维数据,需要对其进行低维表示,常用的方法是选取基函数对其进行基展开。在函数型数据分析中经常使用的基函数有B-样条基函数、傅里叶基函数、小波基函数等。文中选取B-样条基函数对系数函数β(t)进行基展开为
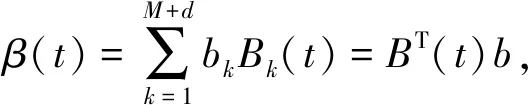
(3)
式中:B(t)----定义在区间[0,T]上的d次B-样条基,B(t)=(B1(t),B2(t),…,BM+d(t))T;
b----对应的系数向量,b=(b1,b2,…,bM+d)T。
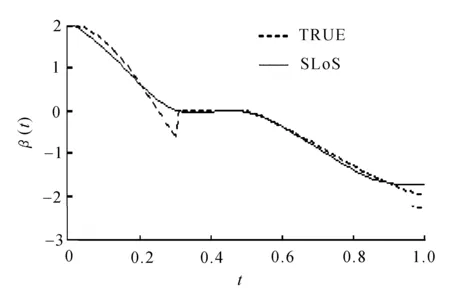
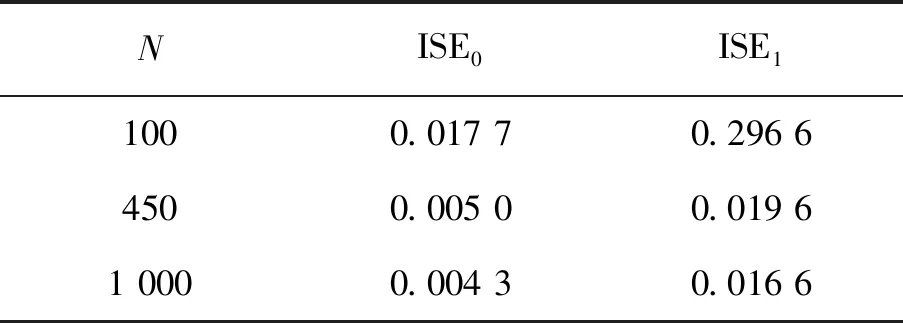
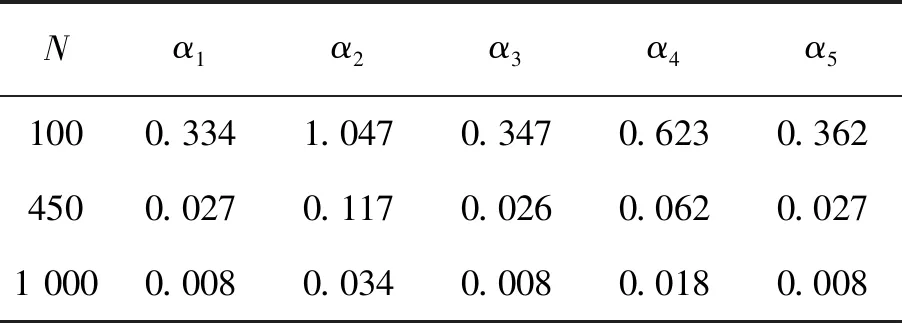
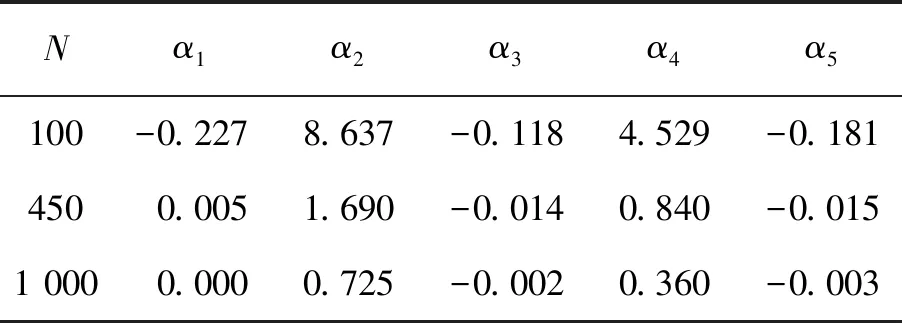
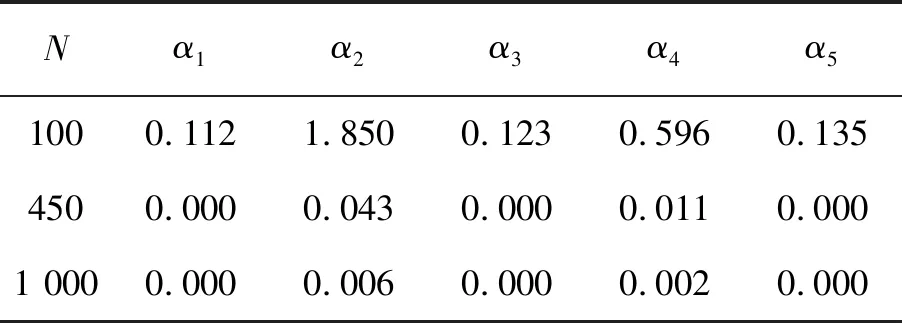
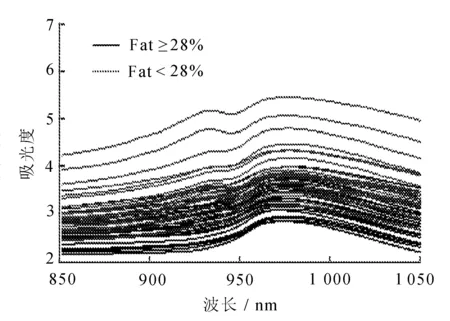
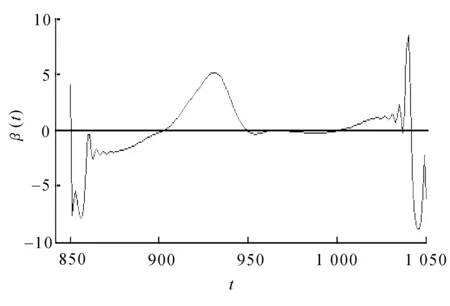
在区间[0,T]上设置M+1个等距结点将区间分成M个等长度的子区间,其中等距结点为0=t0 令U是一个n×(M+d)的矩阵,其中 且 U=(U1,U2,…,Un)T,i=1,2,…,n。 结合式(2)和式(3),对数似然函数可改写为 (4) 令V是一个(M+d)×(M+d)的矩阵,且 1≤i,j≤M+d,则粗糙度惩罚的惩罚函数可改写为 γ‖Dmβ‖2=γbTVb。 (5) (6) 其中 令Wj是一个(M+d)×(M+d)的矩阵,具体形式为 采用Fan J等[15]提出局部平方近似(LQA)方法对式(6)中的稀疏惩罚项进行近似。即给定初始值β(0),有 G(β(0)), (7) 其中 令 (8) 则有 (9) nγbTVb-nbTW(0)b- G(β(0))-nαTΣα。 可见β(t)的优化问题等价于b的优化问题。由于G(β(0))不依赖于β,因此其对b的优化没有影响,惩罚似然函数可改写为 nγbTVb-nbTW(0)b-nαTΣα。 (10) 分别求得式(10)中b和α的一阶导数和二阶导数为: 2nγVb-2nW(0)b, (11) 2nγV-2nW(0), 2nΣα, 2nΣ。 1)通过下式获得b和α的初始估计值 nγbTVb-nαTΣα; 2)通过式(11)在每一次迭代中更新b和α,同时也对W(0)和Σ进行迭代更新 b(m+1)=b(m)- α(m+1)=α(m)- 通过模拟研究提出SLoS估计方法的数值性能,数据由以下模型产生 logitP(Yi=1|Xi(t),Zi)=μ+ (12) i=1,2,…,n。 协变量函数Xi(t)基于等式 Xi(t)=∑aijBj(t) 来生成,其中aij服从标准正态分布,每个Bj(t)是101个具有98个等距结点的5阶B-样条基函数。对于数值型协变量,令Z1,Z2,…,Z5为来自独立同分布的正态分布的样本,回归系数α=c(0,2,0,1,0),且Xi(t)和Z1,Z2,…,Z5独立。 在模拟中,令μ=0,考虑既包含非空子区间,又包含空子区间的β(t), 将上述假设代入模型(12)中,考虑了三种不同样本容量N=100,450,1 000下的系数函数β(t)的估计。绘制样本量N=1 000时,β(t)的SLoS估计曲线与β(t)的真实曲线,如图1所示。 图1 β(t)的SLoS估计曲线 β(t)的估计效果由空子区间和非空子区间上的积分平方误差的大小来决定,分别定义如下: 式中:l0----β(t)的空子区间长度; l1----β(t)的非空子区间长度。 表1 β(t)的ISE0和ISE1 根据表1发现,β(t)的空子区间ISE0和非空子区间ISE1都有随着样本量的增大而减小的趋势。结合图1可知,SLoS方法可以较准确识别空子区间和非空子区间,是一种比较有效的估计方法。 α估计值的表现通过标准差、偏差和均方误差体现。将α在样本量为N=100,450,1 000时的标准差、偏差和均方误差,分别汇总见表2~表4。 表2 α的标准差(×10-3) 表3 α的偏差(×10-4) 表4 α的均方偏差(×10-6) 由上述表中可以明显看出,随着样本量的增大,α估计的标准差、偏差和均方误差都在减小。综上可知,函数型Logistic模型对系数函数β(t)和回归系数α都给出了良好的估计,证明该模型是有效的。 数据来源于http://lib.stat.cmu.edu/datasets/tecator的Tecator数据集。该数据集包含以百分比为单位的215个碎肉样本的脂肪含量、水含量和蛋白质含量。光谱数据的每个样本记录了在波长为[850 nm,1 050 nm]上的100个观测通道下的光谱吸光记录。将该数据集中脂肪含量高于28%的54块碎肉判定为具有一定肥胖特征的样本,脂肪含量低于28%的161块碎肉判定为不具有肥胖特征的样本。从两类样本中各随机抽取30条光谱曲线如图2所示。 图2 两类样本的部分光谱曲线 首先对数据进行预处理,然后使用函数型Logistic模型进行实例研究 logitP(Yi=1|Xi(t),Zi)=μ+ (13) 式中:Yi=1----样本具有一定的肥胖特征; Xi(t)----光谱数据; Z1----水的含量; Z2----蛋白质的含量。 在对该实例进行分析时,主要探究光谱数据的各段波长范围是否对判定肥胖特征有显著影响。在对碎肉样本是否具有肥胖特征的研究中使用提出的SLoS估计方法分析上述问题,得到β(t)的估计曲线如图3所示。 图3 β(t)的估计曲线 由图3可以发现,波长在[960 nm,980 nm]时,光谱数据对肥胖特征的判定没有影响。 面向协变量为函数型和数值型混合数据的二分类问题,提出一种基于Logit变换的函数型 Logistic回归模型。通过数值模拟验证了该方法的有效性,并将该模型应用于Tecator数据集进行实例分析。实证结果表明,波长范围大约在[960 nm,980 nm]时,光谱吸收率对肥胖特征的判定没有影响。文中仅考虑了函数型协变量为单一变量的回归模型,针对多元函数型协变量的函数型Logistic回归模型可作为后续研究。
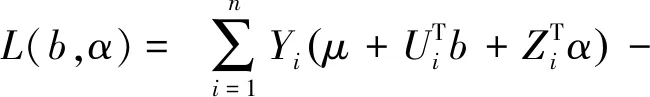
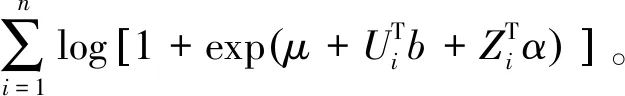
2.1 粗糙度惩罚
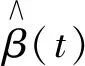
2.2 函数型SCAD (fSCAD)
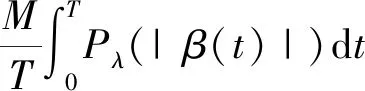
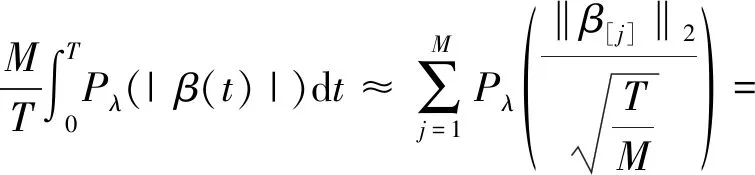
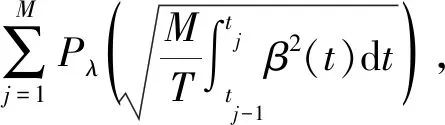
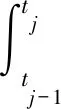
2.3 结合粗糙度惩罚和稀疏惩罚的惩罚似然估计
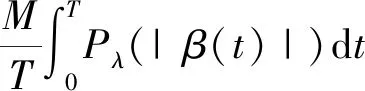
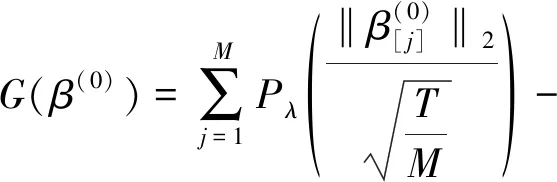
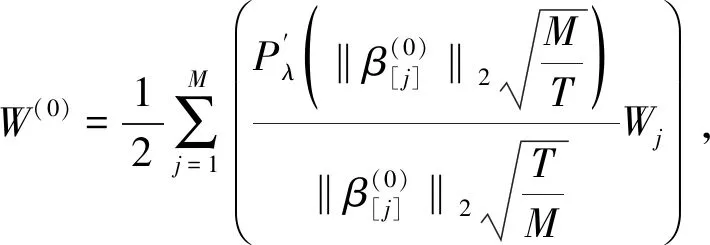
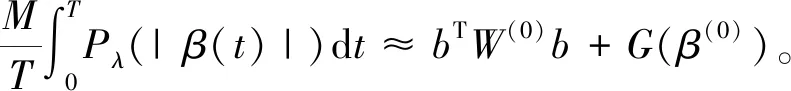
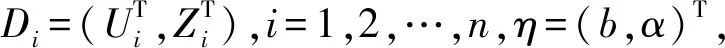
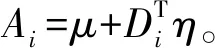
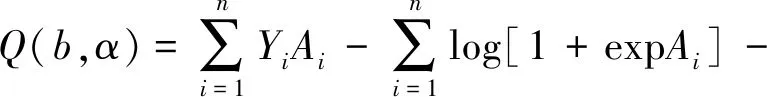
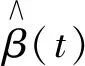
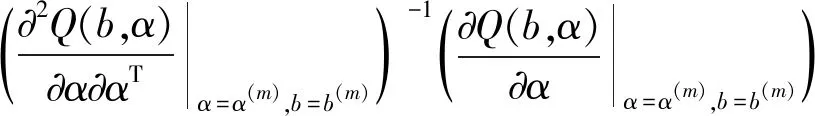
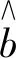
3 数值模拟
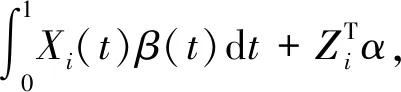
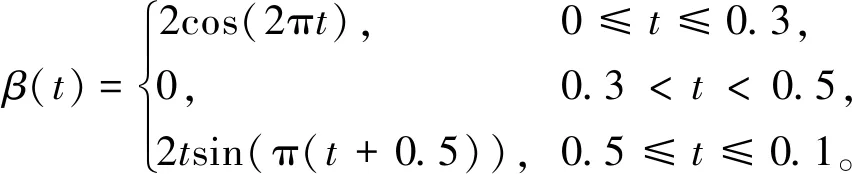
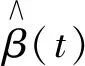
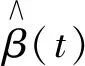
4 实证分析

5 结 语

