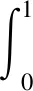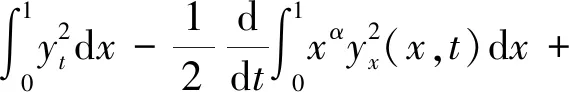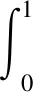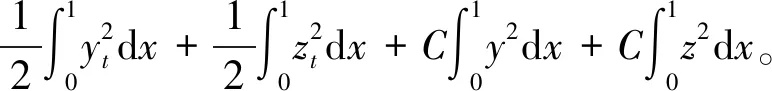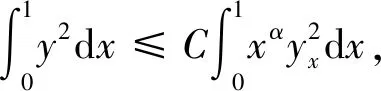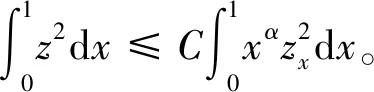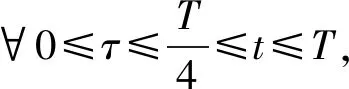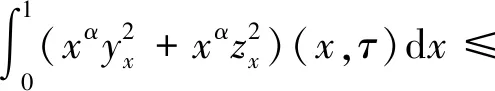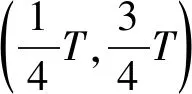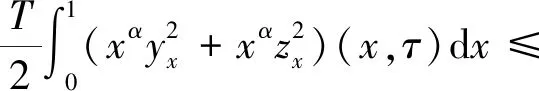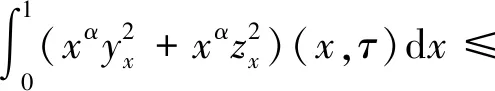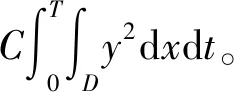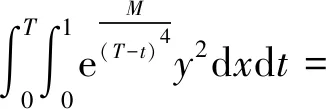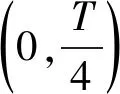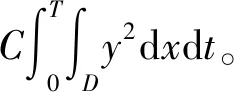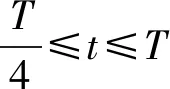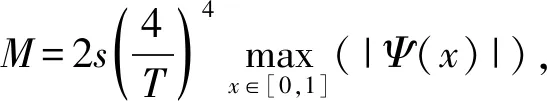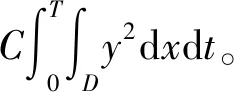一类非齐次耦合弱退化抛物方程组的零可控性
杜润梅, 陈博远, 梅海婷
(长春工业大学 数学与统计学院, 吉林 长春 130012)
0 引 言
偏微分方程来源于物理、化学、生物、天文学等学科,由于它具有广泛的应用背景,一直是备受学者关注的研究领域。抛物方程是偏微分方程的基本方程之一,可以用来描述反映扩散模型、热量传播模型等,抛物方程组可以用来描述生物种群模型。在实际问题中,退化的抛物方程能更好地模拟实际问题,因而吸引了越来越多学者的关注.文献[1-4]研究了在边界退化抛物方程的能控性,文献[5-7]研究了在边界退化抛物方程组的能控性。具体来说,文献[5]研究了退化抛物方程组
ut-(xαux)x+c(x,t)u=g+hχD, (x,t)∈QT,
vt-(xαvx)x+d(x,t)v=uχD, (x,t)∈QT,
的初边值问题的零能控性,其中0<α<2,QT=(0,1)×(0,T),c,d∈L∞(QT),D=(a,b)是(0,1)上的非空真子集,χD是D上的特征函数,g∈L2(QT),h是控制函数。文献[6]研究了退化抛物方程组
ut-(xαux)x+C11(x,t)u+C12(x,t)v=hχD,
(x,t)∈QT,
vt-(xαvx)x+C21(x,t)u+C22(x,t)v=0,
(x,t)∈QT,
的初边值问题的零能控性,其中0<α<2,C11,C12,C21,C22∈L∞(QT),h是控制函数。文献[7]研究了n个方程,m个控制函数的退化抛物方程组的能控性。文中研究如下退化抛物方程组的初边值问题的零能控性:
ut-(xαux)x+C11(x,t)u+C12(x,t)v=g+hχD,
(x,t)∈QT,
(1)
vt-(xαvx)x+C21(x,t)u+C22(x,t)v=0,
(x,t)∈QT,
(2)
u(0,t)=u(1,t)=v(0,t)=v(1,t)=0,
t∈(0,T),
(3)
u(x,0)=u0(x),
v(x,0)=v0(x),x∈(0,1),
(4)
其中0<α<1,C11,C12,C21,C22∈L∞(QT),u0,v0∈L2(0,1),g∈L2(QT),h是控制函数。
假设存在a1,b1,μ>0满足a≤a1 (5) 定义Hilbert空间 其中 eM(t)=exp(Mt-4)。 文中主要结果有如下定理。 定理1存在一个正数M=M(D,T),使得当g∈L2(eM(T-t)),u0,v0∈L2(0,1)时,存在h∈L2(QT),问题(1)~(4)的解满足 u(x,T)=v(x,T)=0。 众所周知, 问题(1)~(4)的零能控性等价于其对偶系统的可观测性。因此,文中主要证明对偶系统的能观不等式。 关于退化抛物方程的适定性及Carleman估计, 考虑方程 wt+(xαwx)x+c(x,t)w=F, (x,t)∈QT, (6) w(0,t)=w(1,t)=0,t∈(0,T), (7) w(x,T)=wT(x),x∈(0,1), (8) 其中,c∈L∞(QT),F∈L2(QT)。 定义 由半群理论, 可以得到问题(6)~(8)的适定性。 引理1[1]令F∈L2(QT)对于wT∈L2(0,1),问题(6)~(8)存在一个唯一解 H1(0,T;L2(0,1))。 注1由引理1可得问题(1)~(4)的适定性。 定义 Ψ1(x)=x2-α-2, Ψ2(x)=e2rξ(0)-erξ(x),x∈[0,1], Ψ(x)=ζ(x)Ψ1(x)-(1-ζ(x))Ψ2(x), φ(x,t)=θ(t)Ψ(x),x∈[0,1]。 有如下Carleman估计。 引理2[1]存在两个正常数C,S0,使得对所有s≥S0和问题(6)~(8)的解w,有 其中M(s)是依赖于s的常数。 问题(1)~(4)的对偶系统 yt+(xαyx)x-C11(x,t)y-C21(x,t)z=0, (x,t)∈QT, (9) zt+(xαzx)x-C12(x,t)y-C22(x,t)z=0, (x,t)∈QT, (10) y(0,t)=y(1,t)=z(0,t)=z(1,t)=0, t∈(0,T), (11) y(x,T)=yT(x), z(x,T)=zT(x),x∈(0,1), (12) 其中yT,zT∈L2(0,1)。 命题1存在两个正常数C,S1,使得对所有s≥S1和式(9)~式(12)的解(y,z),有 s3θ3x2-αz2)e2sφdxdt≤ 证明 由引理2,存在C1,C2和S1,使得对所有s≥S1,有 (13) (14) 设P(x,t)=z(x,t)e2sφ,(x,t)∈QT,由z(0,t)=0,可得P(0,t)=0, (15) 由φ定义: ∬QTz2e2sφdxdt≤ 取s充分大,使 有 则有 ∬QTz2e2sφdxdt≤ (16) 同理,若取s充分大,使 则有 ∬QTy2e2sφdxdt≤ (17) 由式(13)、(14)、(16)、(17), 可得当 时, 定理2存在s和C,使得 0≤ζ1(x)≤1, 0 ζ1(x)=1,x∈O, ζ1(x)=0,x∈(0,1)(a2,b2), 且 其中 注意到 和边界条件式(11), 分部积分可得 I1+I2+I3+I4。 (18) I1=0。 (19) 由Hölder不等式, (20) 其中δ1待确定,C(δ1)是与δ1有关的常数。 (21) 由命题1及ζ1(x)=1,x∈O,有 (22) (23) 综合式(21)~式(23)和式(5),有 由命题1, 可得定理2。 定理3存在充分大的M>0和C>0,使得式(9)~式(12)的解满足 证明 在式(9)两边乘yt,式(10)两边乘zt,相加并在(0,1)上积分,得 (24) 类似于式(15)的证明,有 (25) (26) 因此, 由式(24)~式(26), 即 故,由定理2, (27) 由式(25)~式(27), (28) (29) (30) 由式(30)和定理2 (31) 由式(28)、 式(29)、 式(31)可得 由于对偶问题的能观性等价于原问题的零能控性,定理1得证。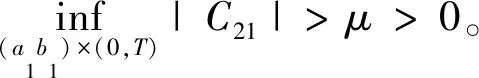
1 退化抛物方程的适定性及Carleman估计

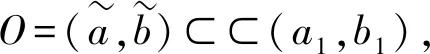
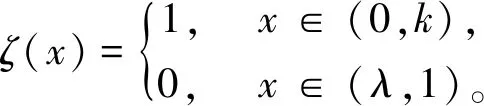
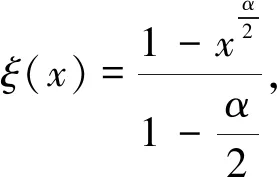
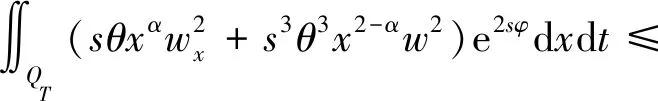
2 对偶系统的Carleman估计
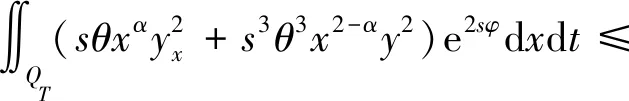
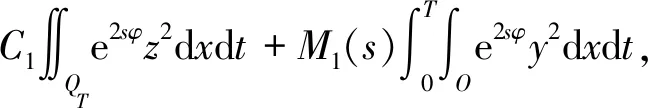
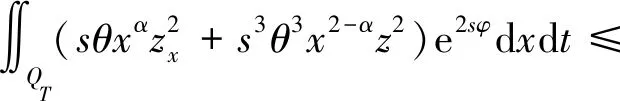
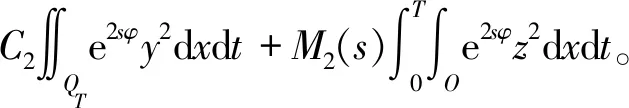
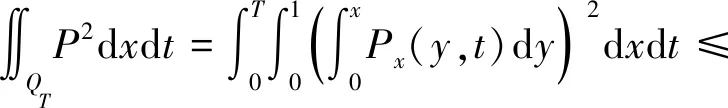
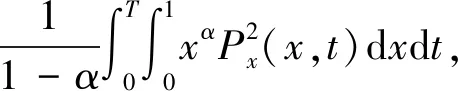
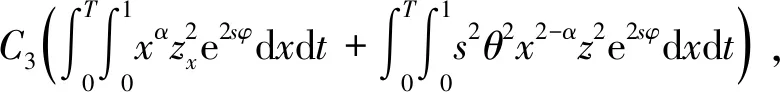
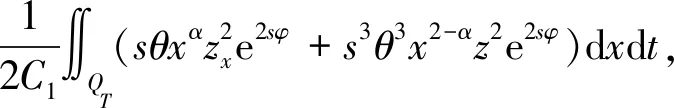


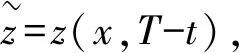
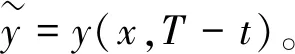
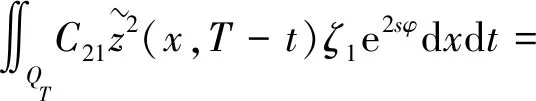
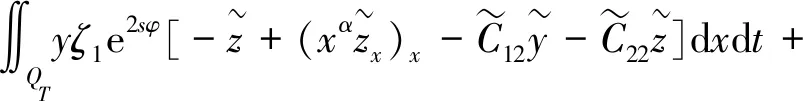

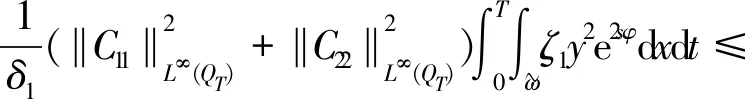
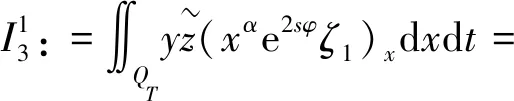
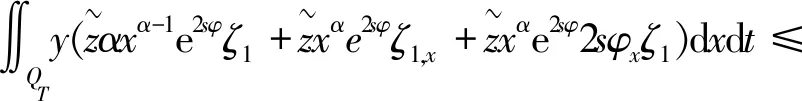
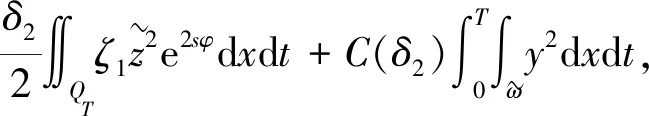
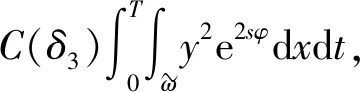
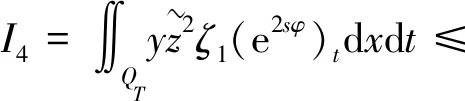
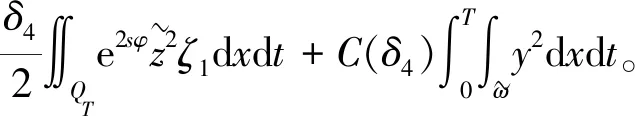
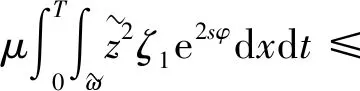
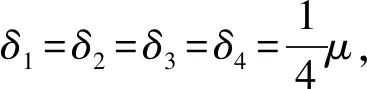
3 能观不等式