知识交汇 思维多样——一道面积最值问题的探究

江苏省扬州市邗江区第一中学 潘月妹

涉及三角形面积的最值问题，是解三角形问题中的一类基本综合应用问题．此类问题巧妙融入解三角形问题、最值应用问题等，交汇平面几何、三角函数、函数与方程、不等式等相关知识，是新高考数学试卷中比较常见的一类综合应用性问题，充分体现高考“在知识交汇处命题”的指导精神，倍受各方关注．

1 问题呈现

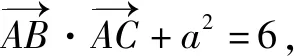
此题以三角形为几何背景，结合平面向量的数量积、解三角形等知识来确定三角形面积的最值．题目简单明了，可以从问题背景出发，利用解三角形思维从平面几何来直观切入；也可以从平面向量知识出发，利用平面向量的坐标运算或对应公式等思维视角来切入．视角不同，解题思路与过程以及涉及到的知识点也各不相同，各有各的精彩．

2 问题解决

方法1:解三角形法.

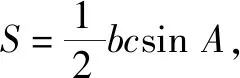
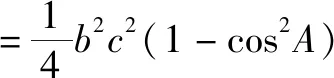
利用基本不等式，可得

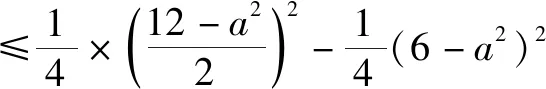
所以，当a2=4，即a=2，b=c=2，亦即△ABC为边长为2的正三角形时，S2取得最大值3.

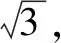
点评：通过解三角形思维来解决三角形中的面积问题，是解决此类问题最常用的一种技巧方法．在具体解析过程中，综合了平面向量的数量积、解三角形的余弦定理与三角形面积公式、三角公式、基本不等式以及二次函数的图象与性质等众多知识，实现多知识交汇与融合的完美统一．

方法2：平面几何法.

图1

如图1所示，设h为BC边上的高，对应的垂足为点D.设|BD|=x，则|CD|=a-x.

结合勾股定理，有a2+b2+c2=a2+x2+h2+(a-x)2+h2=12.整理可得

x2-ax+a2+h2-6=0 ①

由于关于x的二次方程①有解，则

Δ=a2-4(a2+h2-6)≥0.

整理，可得3a2+4h2≤24.

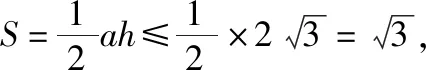
点评：根据条件，借助平面向量的数量积公式与余弦定理，得到三角形的三边的平方和的值，巧妙构建平面几何图形，利用三角形的直观性，结合勾股定理的应用，综合二次方程有根的条件，并利用基本不等式来转化与应用．数形结合，直观有效．

方法3：建系法.

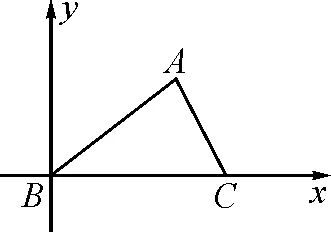
图2

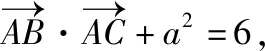
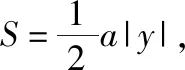
所以，当a2=4，即a=2，b=c=2，亦即△ABC为边长为2的正三角形时，S2取得最大值3.

点评：通过建立平面直角坐标系，结合点的坐标，解决平面向量的数量积以及三角形的面积等相关问题，也是解决解三角形问题的一种基本技巧方法．通过配方处理，利用参数的取值限制并借助二次函数的图象与性质来确定最值，思路清晰，方法常规，运算量合适．

方法4：极化恒等式法.

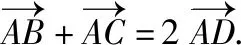
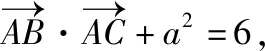
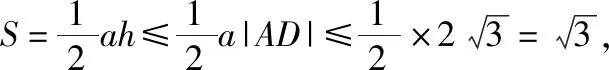
点评：利用平面向量中的极化恒等式将平面向量的数量积关系转化为对应边长的关系，为进一步解三角形指明方向．利用平面向量的极化恒等式可以快速对平面向量的数量积进行化归与转化，体现了平面向量的几何属性，特别适合于以三角形为载体且含有线段中点的平面向量问题．

方法5：外森比克不等式法.

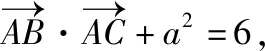
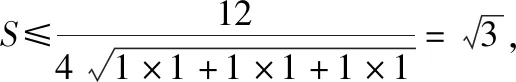
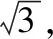
3 变式拓展

探究：根据以上问题中方法1(或其他方法)的解析过程，改变问题条件的视角，从三角形三边的平方和的值所提供的信息入手，进而确定对应三角形面积的最值，从而得到以下对应的变式问题．

变式△ABC的内角A，B，C的对边分别为a，b，c，若a2+b2+c2=12，则△ABC面积的最大值为( ).

解析：由a2+b2+c2=12，结合余弦定理可得bccosA+a2=6.

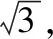
当然，利用变式1中的条件，解决问题的思路更加活跃，方法更多，这里就不多加叙述．

4 教学启示

(1)面积应用，最值综合

借助三角形面积这一基本要素，可以巧妙利用三角形面积的夹角公式、高线公式、圆的半径公式以及海伦公式等的应用，合理构建三角形中相关边、角等元素之间的关系，巧妙渗入函数与方程、基本不等式、函数与方程、平面几何等相关知识，通过代数运算、逻辑推理、几何直观等，实现最值的确定与求解．

(2)一题多解，一题多悟

结合实例，针对具体问题从多个不同思维角度来切入与处理，巧妙把对应问题的底蕴充分挖掘出来，多角度出发，多方法求解，从而真正体现对数学知识的融会贯通，展现数学基础知识之间的交汇与融合，全面提升能力，拓展思维．巧妙借助一题多解，真正达到在学中“悟”、在“悟”中不断提升解题技能，进而达到一题多悟的良好效果．