线性代数课程思政教学的案例探索与实施

范莉霞, 陈 明

(嘉兴学院 数据科学学院，浙江嘉兴314001)

2016年12月，习近平同志在全国高校思想政治工作会议中明确指出：“要用好课堂教学这个主渠道，思想政治理论课要坚持在改进中加强，提升思想政治教育亲和力和针对性，满足学生成长发展需求和期待，其他各门课都要守好一段渠、种好责任田，使各类课程与思想政治理论课同向同行，形成协同效应.”[1]2019 年 3 月，习近平在学校思想政治理论课教师座谈会上再次指出：“要挖掘其他课程和教学方式中蕴含的思想政治教育资源，实现全员全程全方位育人.”[2]2020 年 4 月，《教育部等八部门关于加快构建高校思想政治工作体系的意见》也对此作了明确要求：“健全立德树人的教育体制机制，加快构建高校思想政治工作体系，全面推进所有学科课程思政建设.”[3]以立德树人为根本任务的课程思政这一教育理念，已经成为中国高等教育的必然趋势，所有课程的教学工作都肩负着价值引领的责任.线性代数作为一门大学数学专业的基础课程，其课程思政建设对于立德树人教育目标的实现具有重要意义.

1 线性代数课程思政教学的特点

作为一门大学数学基础课程，线性代数有其自身的特点，开展课程思政建设也有相应的优势和劣势.

线性代数课程具有数学类课程的普遍特征，即科学严密、逻辑性强，其研究对象反映了客观存在的自然规律，具有高度抽象性和普适性，学生对于课程的基本概念、理论、运算方法和技巧等知识层面的掌握有一定的挑战，因此线性代数思政教育具有一定的难度.

1.1 优势

1.1.1 课程地位重要.作为高等院校一门重要的公共基础课，线性代数在数学专业考研课程中占有相当比重，学生对于课程的重视程度较高，在该课程中开展思政教育，往往效果也较好.

1.1.2 课程受众范围广泛.线性代数课程是理工、经管类专业的一门必修课，受众范围广泛，使得在线性代数课程教学中进行思政育人更有效果和意义.

1.1.3 听课对象处于价值观形成的重要时期.通常情况下，线性代数作为一门专业基础课程，其开课时间一般都选在大一下学期或大二上学期，面对的都是刚入高校不久的学生，此时是学生价值观形成和确立的关键时期，在这一时期对其进行潜移默化的思政教育，收效会更好.

1.1.4 课程蕴含的思政元素丰富.线性代数在数学史、数学应用、数学思想和数学文化等多个维度蕴含着丰富的思政元素，深入挖掘这些元素，能帮助学生增强文化自信和民族自豪感，强化数学思维和应用意识，培养科学精神，树立正确的世界观、人生观和价值观.

1.2 劣势

在教学过程中，线性代数这门课程是专业基础课程，是学习计算机等其他课程的基础，由于逻辑性强，对学生来说，掌握好课程的基本概念、理论、运算方法和技巧等知识层面就有一定的挑战；对教师来说，让学生在学好这门有一定难度的专业课程的同时也能受到课程思政教育，也是一项比较艰巨的任务.

2 线性代数课程思政教学设计思路

要做好课程思政，首先要做好课程思政的顶层设计.嘉兴学院线性代数课程团队常年从事该课程的教学和科研工作，并一直遵循“寓德于业、以业传德、以德促业、德业并重”的教学理念，多维度深挖思政元素，多手段实现有机融入，多层次确保育人效果.第一，在课程教学过程中结合数学史和数学家故事，坚定学生的文化自信，激发其民族自豪感和使命担当的家国情怀；第二，通过讲解线性代数课程知识在相关领域的应用，强化学生的数学应用意识，培养学以致用、精益求精的科学精神和勇于创新的品质；第三，借助线性代数课程蕴含的数学文化、数学思想和数学方法论，引导学生感受数学魅力，培养其数学精神，并通过日常的数学思维训练，提升学生的逻辑推理能力，培养科学理性的思维方法.第四，通过教学实施，力求学生明晰该课程中的思想内涵、应用价值、美学元素、思辨精神，引导学生“学、思、践、悟”，实现“知识传播、能力培养、价值引领”三位一体的立德树人目标.

3 线性代数课程思政教学案例分析

3.1 回顾课程发展史，深挖思政元素——重塑线性代数第一课,启发开放思维

本案例以课程简介为主线，挖掘思政元素，具体设计思路如图1所示.

图1 线性代数第一课案例思政设计思路

第一，追溯起源.线性代数最早可见于公元1世纪前后成本的《九章算术》，其中对于线性方程组解法的研究早于西方1500年左右，以此激发学生的民族自豪感，增加民族自信.

第二，介绍发展史.由近代数学发展史可知，在17世纪到19世纪这段时间，在线性代数的发展过程中几乎没有中国数学家的身影，线性代数这一概念是1859年由李善兰翻译引入中国的.

李善兰(1811-1882)，浙江海宁人，是中国近代著名的数学、天文学、力学和植物学家，创立了二次平方根的幂级数展开式，研究各种三角函数、反三角函数和对数函数的幂级数展开式(现称“自然数幂求和公式”)，这是李善兰也是19世纪中国数学界最重大的成就.课程组立足本土，介绍嘉兴名人李善兰，深挖文化根脉，并通过对李善兰生平事迹的介绍深入分析近代中国落后挨打的原因.引导学生讨论与思辨：

☆坚定科学技术是核心生产力的认知，以此激发学生科技报国、使命担当的爱国主义情怀；

☆介绍“闭关锁国”的历史背景，启迪学生要用“开放融合”的思维方式思考和解决问题.

第三，思维延展.从近代的马克思主义思想引入,到中国的改革开放,进一步提炼出本案例的核心思想——倡导开放融合，古往今来,人类从闭塞走向开放、从隔绝走向融合是不可阻挡的时代潮流.进一步引导学生展开讨论，思辨、认知开放融合的必要性和重要性.

3.2 探究知识应用，挖掘思政元素——以特征值与特征向量的应用为例

线性代数中，矩阵的特征值与特征向量是一个重要内容，这一知识点在工程技术、经济管理以及其他许多学科中都有着广泛应用.通过本案例的介绍，旨在强化学生的数学应用意识，引导学生坚定理想信念，培养科学精神，提升学生精益求精、学以致用、勇于创新的品质.特征值与特征向量的应用课程思政教学案例具体设计思路如图2所示.

图2 特征值与特征向量的应用课程思政案例具体设计思路

第一，以2020年5月5日广东虎门大桥和1940年当时世界第三大桥美国华盛顿州的塔科马海峡大桥的共振现象为切入点，介绍共振现象与特征值、特征向量的关系，突出特征值与特征向量在桥梁建造中的应用价值，培养学生的数学应用意识，提升数学素养.回顾中国桥梁建造史上的几个代表作，如古代赵州桥、现代南京长江大桥和当代港珠澳大桥，激励学生增强民族自信心，坚定文化自信.

第二，通过对特征值与特征向量在其他领域，比如层次分析法、搜索引擎Google的Page Rank技术、图像处理、压缩感知等方面的应用介绍，引用美国《关于21世纪国家科技发展战略报告》以及数学家华罗庚先生、华为总裁任正非等人关于数学的言论，展示数学本身潜在的巨大的应用价值及其对于科技的推动作用.引导学生讨论、认知：

☆科技发展离不开数学基础；

☆要有学以致用、精益求精的科学品质，具备科学精神.

第三，思维延展.特征值和特征向量，不仅有着广泛的应用，还蕴含着丰富的人生哲理.特征向量代表着线性变换的一个稳定的方向，当特征值为正时，其方向不会改变.以这些特征启迪学生在人生成长道路中，正确、稳定的方向选择极其重要.引导学生思辨、认知：

☆在人生的每一个阶段，都要把握好正确的方向；

☆坚守初心牢记使命永不动摇.

3.3 从数学与哲学的统一关系中挖掘思政元素——以矩阵初等行变换为例

矩阵的初等行变换是线性代数中研究矩阵的一种重要手段，围绕矩阵在初等变换下的“形变质不变”规律，从科学、文学、哲学、生活等多个维度挖掘“形变质不变”中蕴含的深刻思想与丰富内涵，培养学生运用“形变质不变”的辩证思维分析、处理各种实际问题的意识和能力，塑造科学精神，具体设计思路如图3所示.

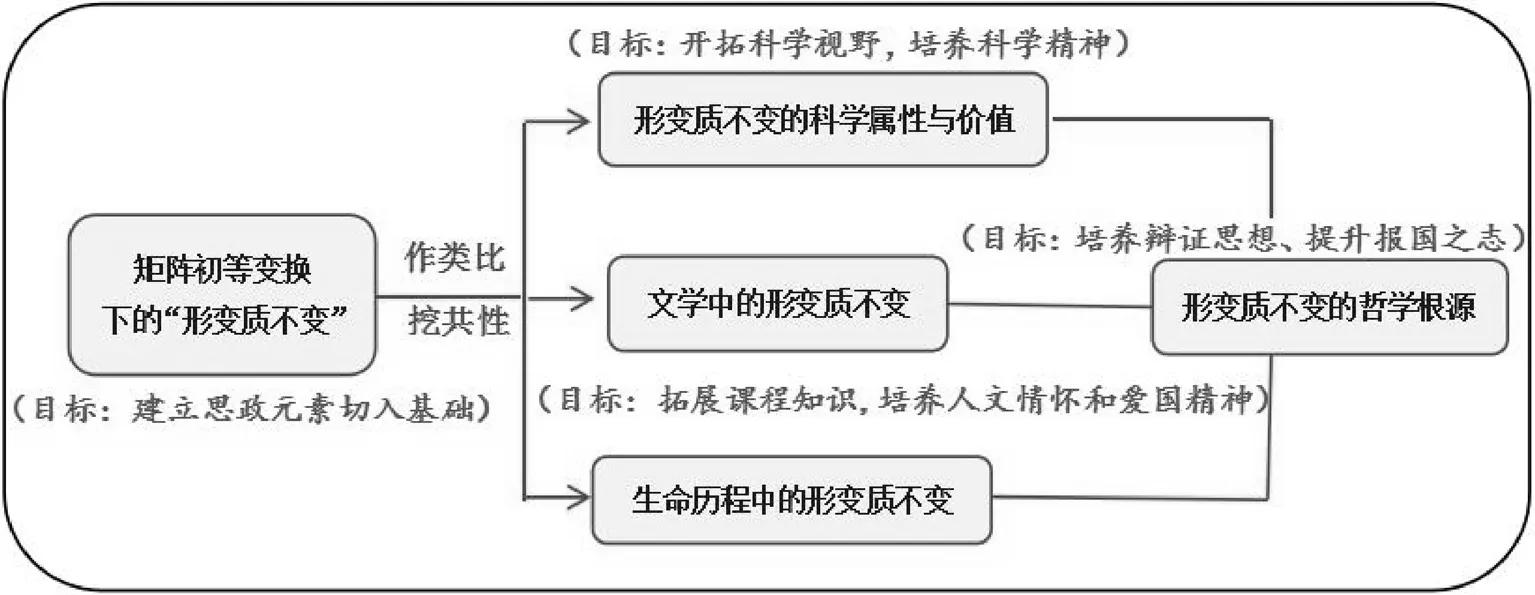
图3 矩阵初等行变换课程思政案例设计思路

第一，矩阵的初等行变换主要包含换行变换、倍乘变换和倍加变换三种.在初等变换下，虽然矩阵的形态都发生了改变，但很多内在的性质是保持不变的，如：矩阵的秩不变，列向量组的秩不变，列向量的线性相关性不变，列向量的线性表示形式不变，极大线性无关组的位置不变，以该矩阵作为增广矩阵的线性方程组的解不变，等等.矩阵的初等行变换的规律体现了一个基本的哲学原理，那就是——“形变质不变”，这个原理不仅在代数变换中存在，而且在我们的大千世界、万事万物及各个领域中也普遍存在.

第二，在哲学、科学、文学、生活等多个范畴找关联、作类比、挖共性，揭示各领域中存在的“形变质不变”的现象和规律，挖掘其与代数学中“形变质不变”的联系，反映事物发展变化中的数学本质，展示数学作为一种文化体系的博大精深，揭示各学科在思想理念上的深刻联系.

第三，“形变质不变”是哲学范畴的基本原理.辩证唯物主义认为，事物的运动是绝对的，变化是永恒的，没有运动和变化就没有发展和进步.变与不变是辩证统一的，万变不离其宗.毛泽东同志将马克思列宁主义普遍真理和中国革命具体实践相结合，探索出一条适合中国国情的新民主主义革命道路，取得了最后胜利.中国革命实践就是在“求变”，坚守不变的是马列主义的核心要义和理论精髓.邓小平同志提出“四项基本原则是立国之本，改革开放是强国之路”，改革就是求变求强，但改革不能离开基本原则，基本原则是不变的内涵.我们的改革是在中国特色社会主义道路上不断前进的改革，既不走封闭僵化的老路，也不走改旗易帜的邪路.矢志不渝坚持走中国特色社会主义道路，就一定能实现中华民族伟大复兴的中国梦.

引导学生思辨、认知：

☆正确利用辩证唯物主义思想，运用“形变质不变”的原理观察、分析和处理生活中的相关问题；

☆树立崇高的人生理想，坚定政治信念，强化历史使命感.

3.4 领悟数学思想与数学文化，挖掘思政元素——以范德蒙行列式为例

范德蒙行列式是线性代数中一类特殊的行列式，其构造独特且应用广泛.在教学中，可以通过范德蒙行列式的定义及其计算推导，启发学生感悟数学之美，把握递归推理的数学思想和方法，提升数学素养；通过范德蒙行列式和范德蒙矩阵的应用实例介绍，增强学生学以致用的数学意识，培养科学精神，具体设计思路如图4所示.

图4 范德蒙行列式课程思政案例设计思路

第一，由二阶和三阶范德蒙行列式的结构特点引导学生通过现象归纳共性、总结规律，并引申出n阶范德蒙行列式的定义，进而启发学生分析和把握从特殊到一般、从具体到抽象的推理思想，引导学生从此类行列式形式的规范性，感知数学的结构美、统一美.

第二，由二阶、三阶范德蒙行列式的计算方法及其结果，引导学生推理、猜想得出n阶范德蒙行列式的结果，再由数学归纳法进行严格的理论推导，从而培养学生大胆推理、谨慎求证的思想和开拓性思维.在理论推导过程中，着重强调将低阶范德蒙行列式的分析和计算方法延伸、推广至n阶范德蒙行列式上，引导学生更深层次地把握从特殊到一般、从具体到抽象的归纳推理思想，从而更具体、深刻地理解抽象的数学概念及结论，并感知和领悟数学思想特有的逻辑性和严谨性，提升数学素养.

第三，在范德蒙行列式的基础上，延伸范德蒙矩阵和范德蒙变换的定义，并通过多项式插值、代数恒等式、范德蒙纠删码等应用实例体现其在实际中广泛而重要的应用价值.在代数恒等式的应用实例中，可以用世界知名数学家吴文俊先生在机器证明领域的突出成就激发学生的民族自信和爱国情怀，培养学生尊重科学、热爱科学的精神和精益求精的科学品质，并引导学生在日常学习中，多了解课本知识背后的现实背景，树立正确的学习观，驱动知行合一、学以致用的良好品质.

4 结语

本文从数学史、数学应用、方法论、数学思想与数学文化几个不同角度阐述了线性代数课程思政的案例设计与实施方案，这些方案在教学中取得了初步成效.在今后的课程思政建设中，一是应该持续从多角度不断挖掘思政元素，精心设计教学内容，力求实现“寓德于理，润物无声”；二是要紧跟时代步伐，不断更新教学内容，以突出课程的科学性、应用性与时代性；三是应该不断优化课程思政教育实施和评价体系，强化思政育人效果，提升课程的价值引领作用，争取将线性代数打造成课程思政示范“金课”.