向量运算中的“和差”术
——从2022年浙江省高考数学第17题说起
顾予恒, 王 凯
(1.杭州第二中学钱江学校,浙江 杭州 311215;2.杭州市源清中学,浙江 杭州 310015)
2022年的高考大幕已然落下,各份高考卷中向量内容大都以相对简单的姿态出现,只有浙江卷依然保持较高的难度.这是继2019年后连续第4年以向量问题作为填空题压轴,向量内容在浙江卷中的地位可见一斑.2022年浙江卷第17题选取了圆内接正八边形为背景,主要考查了向量的运算.本文将着重从数与形的视角进行研究,探寻向量运算中的“和差”术背后的奥秘.
1 向量运算“和差”术
众所周知,向量是沟通代数与几何的桥梁,这座桥梁要通过向量运算才能建立起来,因此向量运算在向量问题的研究中处于核心地位,而向量运算的核心则是它的运算法则.
向量的加法、减法、数乘和数量积(a+b,a-b,λa,a·b)是4种常见的运算,它们之间有着紧密的联系.因为向量集数与形于一身,所以其运算性质也应该从几何和代数两个角度来展开研究.
1.1 代数角度
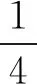
我们可以类比实数的运算,构建出两个重要的等式:
(a+b)2-(a-b)2=4a·b;
(1)
(a+b)2+(a-b)2=2(a2+b2).
(2)
式(1)还可以变形为
a2+b2=(a+b)2-2a·b=(a-b)2+2a·b.
这些等式都是围绕着两个向量的和与差展开的,蕴涵向量的平方和与平方差的结构,因此可以称之为向量“和差”术.
1.2 几何角度
我们可以为式(1)和式(2)这两个恒等式找到几何图形和性质来帮助记忆和理解.
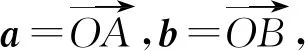
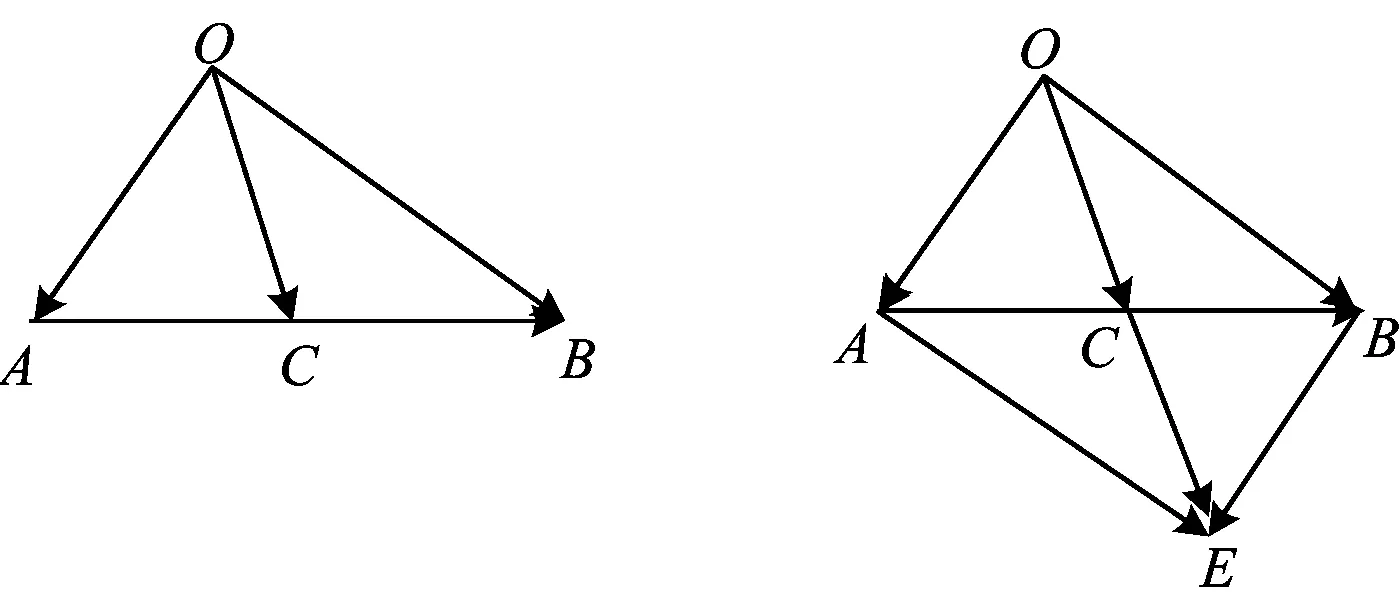
图1 图2
等式(2)可表示为
其几何意义可以表述为三角形的两边平方和等于第三边长的一半与中线长的平方和的两倍,也可以表述为在以a,b为邻边的平行四边形中,两条对角线的平方和等于四边的平方和(如图2).
这两个等式为我们建立起了三角形各边、中线与相应边的数量积,平行四边形对角线长度与相应邻边之间的联系.
2 高考真题与变式
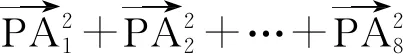
(2022年浙江省数学高考试题第17题)
分析本题要求8个向量的平方和,由于图形具有良好的对称性,因此容易想到“凑对”解决.向量的平方和很自然让人联想到恒等式
解如图3,
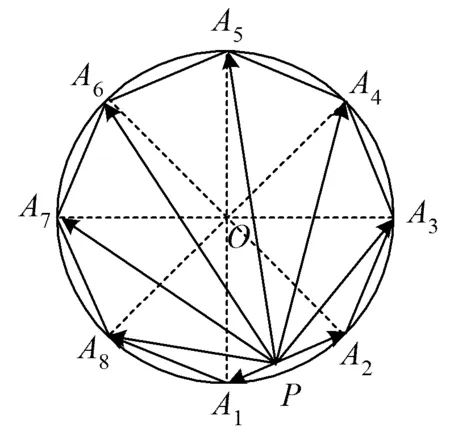
图3
同理可得
因此
在△A1OA2中,
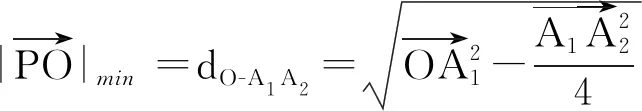
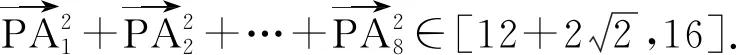
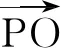
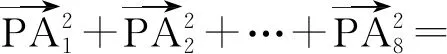
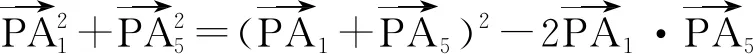
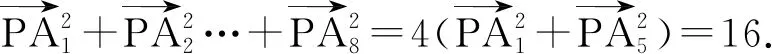
评注变式1将高考题中的点P改为在单位圆上运动,结果变为定值.通过运算研究了直径所对的圆周角为直角的几何性质和勾股定理的定量运算.
变式2(多选题)如图4,正方形ABCD的中心与⊙O的圆心重合,P是⊙O上的动点,则下列叙述正确的是
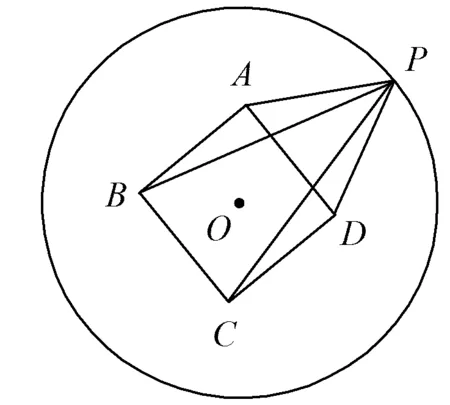
图4
( )
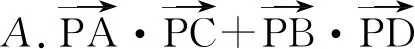
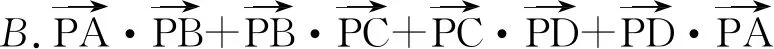
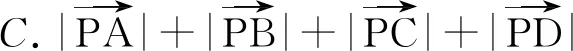
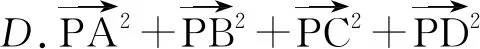
解在选项A中,
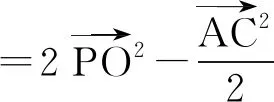
故选项A正确.
在选项B中,
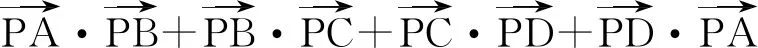
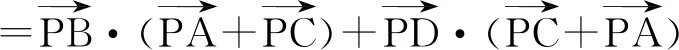
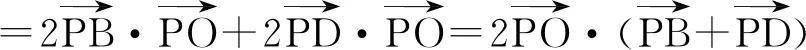
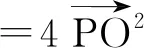
故选项B正确.
在选项C中,取特殊位置即可知显然是错误的.故选项C错误.
在选项D中,
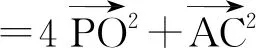
故选项D正确.
因此,正确选项为ABD.
评注变式2将高考题中的内接正八边形变为同心正方形,4个选项分别用到了等式(1)、等式(2),对向量的转化与运算进行了较好地考查.
3 类题研究与拓展
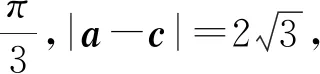
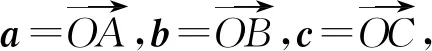
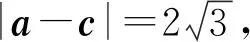
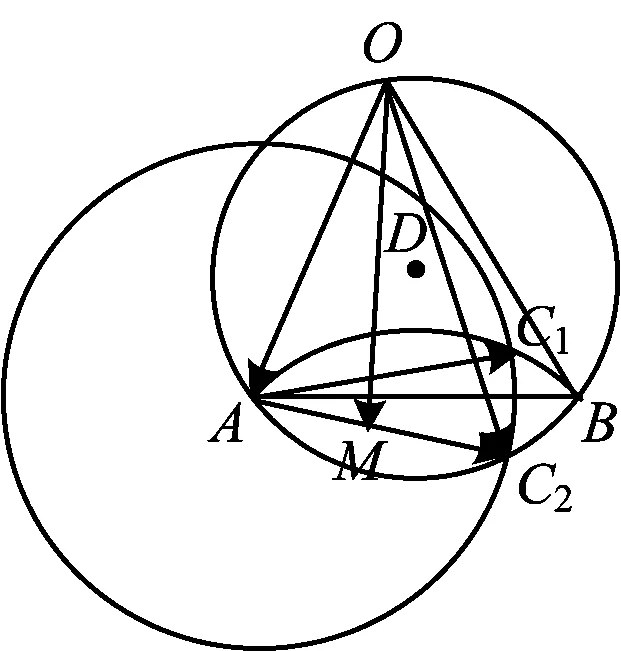
图5
因为要求a2+c2的最大值,显然点C取△OAB外的点C2位置,则
所以
a2+c2≤60.
解法2由解法1可知
从而
于是
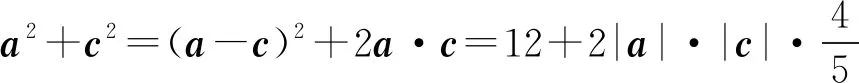
所以
a2+c2≤60.
评注本题首先通过向量表征了外接圆这一几何图形,然后在平面几何背景下,从形的角度研究向量问题.
例3已知圆台上底面半径为3,下底面半径为4,高为7.若点A,B,C在下底面圆的圆周上,且AB⊥BC,点P在上底面圆的圆周上,则PA2+PB2+PC2的最小值为______.
解如图6,
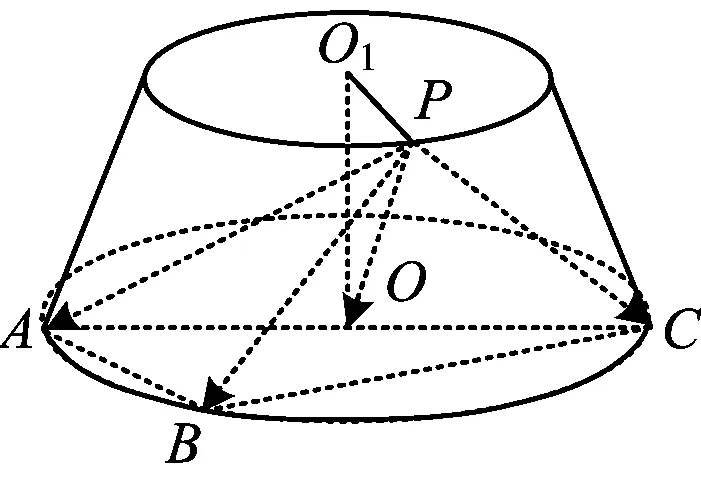
图6
因为圆台的母线长
则
所以
PA2+PB2+PC2≥198.
评注本题是在立体几何背景下,处理两段长度和的问题.
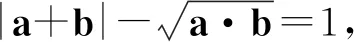
分析题干中出现了|a+b|,a·b,|a-b|这些和差积的基本结构,因此可以利用它们之间的运算关系进行化简,用未知表示已知.
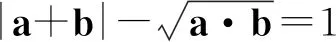
a·b=(|a+b|-1)2.
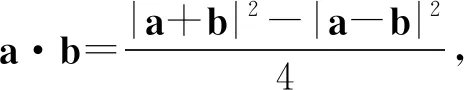
化简得 |a-b|2=-3|a+b|2+8|a+b|-4
故
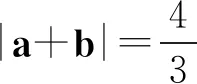
评注本题是在向量代数背景下,熟练运用向量运算公式进行转化和化归.
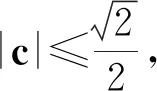
解设a,b的夹角为θ,则
因为a2+b2=1,所以
|a|4+|b|4=1-2|a|2·|b|2,
代入上式,得
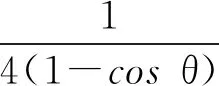
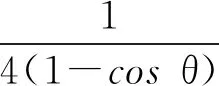
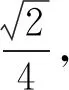
又因为
所以
评注本题是在向量代数背景下,类比实数运算,从数的角度研究向量问题.
4 结束语
向量是学生在高中阶段遇到的一种新的运算对象,而向量运算则是向量内容中的一个核心要点,在历年高考中也是屡见不鲜,常考常新.学生通过向量运算的学习可以加深对运算对象的理解,归纳运算法则和运算律的数学思想,体会研究向量运算性质的数学方法,得出向量运算的基本套路,特别是在用向量解决几何问题的过程中体会向量运算的威力,对提升学生的逻辑推理与数学运算素养有重要意义.
研究高考真题,反思日常教学,我们在课堂中要重视一般观念的思维引领作用,帮助学生类比已有的代数运算体系,归纳出向量运算的内容、路径和方法等,使学生对运算的认知不仅仅停留在“按规则操作”层面,而且对于运算法则有更深的理解.

