对话启智 导图促思

徐 勇

(板浦高级中学，江苏 连云港 222241)

在高三复习中，教师针对性地选取典型试题进行评讲，“一题一课”是常见的方式之一．教学中要体现学生主体参与，教师要事先调研学生对试题的理解与掌握程度，顺应学生的思维特点，找准学生思维的障碍节点．然后，运用启发性提示语展开对话教学，启发学生深入思考，带领学生寻求解题的突破口，直至完全解答试题．最后，教师带领学生绘制思维导图对题目进行回顾与提炼，以解决眼前的试题为载体，学习和掌握思维之道，提升学生的数学学习力．笔者选取一道模拟题的解题教学加以说明．

例1已知A(-1,0),B(3,0),P是⊙O:x2+y2=45上的一个动点，则sin∠APB的最大值为

( )

(2022届江西省南昌市高三一模数学试题第12题)

1 展学生已知，明学生所困

小题大做，课前让学生写出解题过程(或部分解题过程)与遭遇的困惑．笔者进行整理，选取了部分具有代表性的思路进行展示，知晓学生的所想所困．

思路1先求角的余弦值，运用余弦定理寻求角所在两边间的关系.

在△APB中，AB=4，从而

在△AOP中，

PA2=PO2+AO2-2PO·AOcos∠AOP

(1)

在△BOP中，

PB2=PO2+BO2-2PO·BOcos∠BOP

(2)

由于cos∠AOP=-cos∠BOP，式(1)×3+式(2)，得

3PA2+PB2=192．

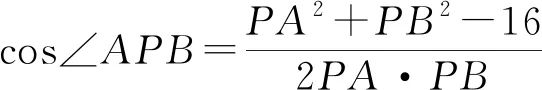
思路2先求角的余弦值，用两点间距离公式表示三角形的两边.

设点P(x0,y0)，则

从而

由余弦定理，得

困惑感觉形式太麻烦，想用导数求最值，但惧于烦琐运算而中途放弃．

思路3先求角的正切值，用角的两边所在直线的倾斜角表示.

设⊙O:x2+y2=45与x轴正半轴交于点Q，则

∠APB=∠QBP-∠BAP，

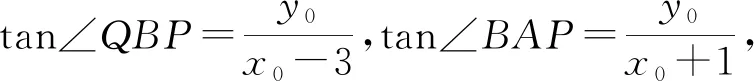
tan∠APB=tan(∠QBP-∠BAP)

困惑最后的表达式既含x0，又有y0，不能视为关于x0的函数，不能用导数求解，不得已而放弃．

2 顺学生思维，寻突破之道

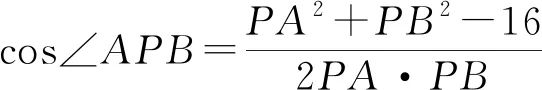
生1：我想用基本不等式，但是分子中有常数16，不是理想的“奇次式”．

师：能否创造条件让表达式变成“奇次式”？

生2：以前我们曾用过“1”代换，这里考虑常数代换．因为3PA2+PB2=192=12×16，所以

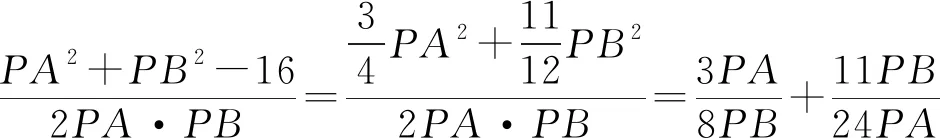
于是

师：漂亮！得益于“1”代换解题经验，借助常数代换，合理构造奇次式，突破障碍，顺利使用基本不等式．

师：对于思路3，设点P(x0,y0)，借助圆方程得

由余弦定理，得

从函数视角直接求导确实比较麻烦，能否设法简化表达式？

生3：让分子简单化．设t=-x0+21，则

x0=21-t，

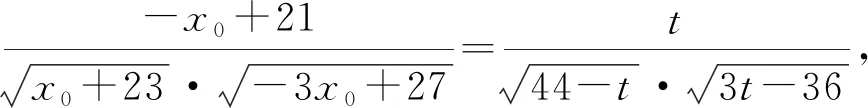
继续让分子简单化，分子分母同除t，得

师：基于先化简后运算的思想，连续变形化简，最后化归为简单的二次函数求最值问题，避开了用导数求最值．上述过程，分母用分子表示，反之，分子能否用分母来表示？

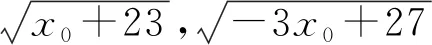
用待定系数法：

-x0+21=m(x0+23)+n(-3x0+27)，

则

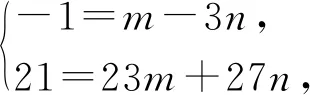
解得

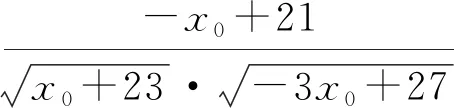
从而

即

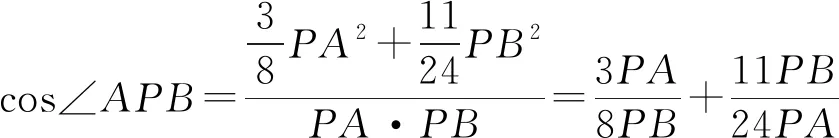
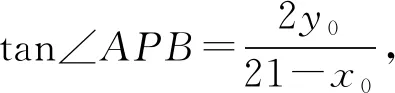
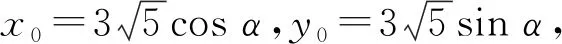
然后运用导数求解．

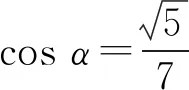
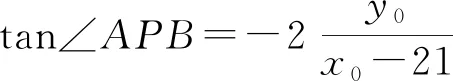
师：续解成功，借助三角函数知识，即圆的参数方程形式．深谙直线的斜率公式，“数”遇困时便思“形”，数转形，继续使用直线与圆的位置关系求解．两种续解方法都是充分利用了圆的方程与性质．

3 画思维导图，发展认识力

师：上述几种思路要么是先求角的余弦最小值，要么是求角的正切最大值．为何不直接求角的正弦值呢？题目为何偏求正弦值呢？

生8：如果直接用正弦，那么只能是正弦定理了，但感觉又不具备使用正弦定理的条件，因为其他角不知道．

师：有道理！由此可联想到三角形的外接圆．

生9：当△ABP的外接圆⊙C与⊙O内切时，△ABP外接圆的直径最小．因为点C在线段AB的垂直平分线x=1上，所以设C(1,t)，则

两边平方，得

即

此时

生10：提到△ABP的外接⊙C，我没有第一时间想到正弦定理，而是将∠APB看作是弦AB所对的圆周角.如图1，联结CA，CB,则

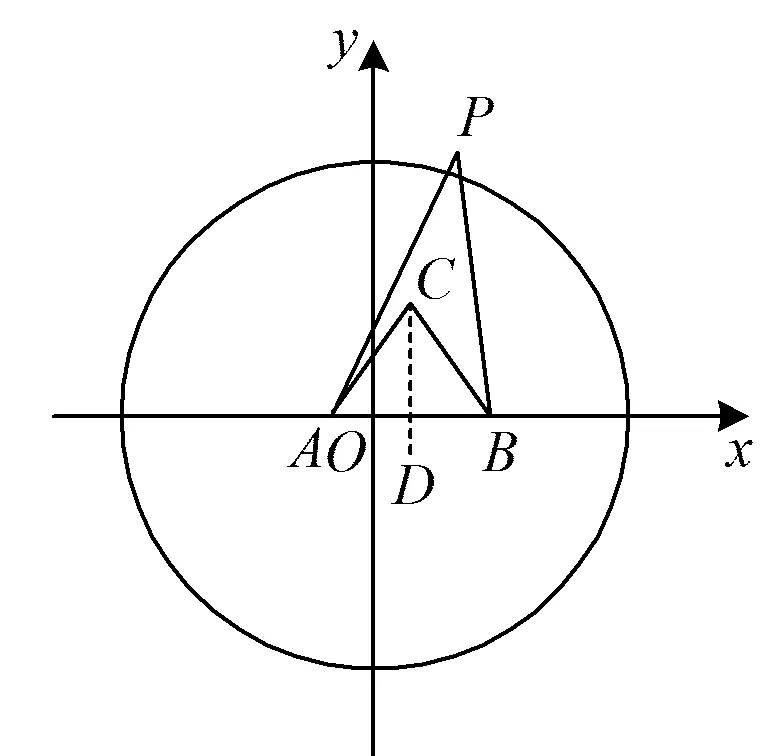
图1

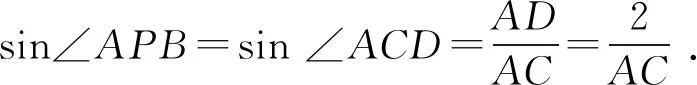
要求sin∠APB的最大值，即求⊙C的半径AC的最小值，易知当⊙C与⊙O内切时半径最小，以下同上．

师：知识没有界限，利用初中所学知识“同弦所对圆周角是圆心角的一半”使得问题更加清晰，运用转化的思想，将sin∠APB变为sin∠ACD，最后转化为两圆特殊的位置关系(内切)．

回顾本题的几种思路与求解历程，尝试用思维导图进行整理，加深对本题的认识与理解．

师生合作，共同绘制如图2所示的思维导图．

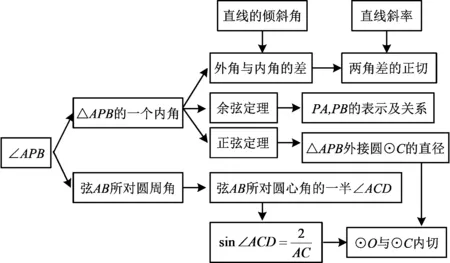
图2

绘制思维导图，便是经过一场头脑风暴对本题进行“复盘”．本题的关键在于对∠APB的定位，初看是△APB的一个内角，也可看作两角的差，亦或视为弦AB所对的圆周角．不同的视角定位决定了后续的运算量的大小，可谓是“多想少算”．解题不仅要方法靠谱，还需要更多的思考．其实，不仅是在解题回顾环节绘制思维导图进行总结提炼，还可前置使用思维导图，即在审题环节画思维导图，多投入时间精力，充分借助思维导图的优势，发散思维，对不同思维触角权衡比较，再聚焦选择思维路径．正如惠特霍斯所说：“一般地，解题之成功，在很大的程度上依赖于一种最适宜的方法．”

4 改已做试题，增题目价值

一线教师要将教学研究的主要精力放在如何突破困扰学生的难点之上，着力挖掘出题目中内在的数学本质，这样才能将新课标的教改精神真正落到实处[1]．本文中教师基于学生想法，顺应学生思维，采用启发性提示语启发思路，突破学生的难点障碍．例1的难点：一是运算之难(创造条件使用基本不等式求最值或简化形式运用函数思想求最值)；二是没有洞察试题本质(圆中定弦所对圆周角)．借助思维导图，能让题目可视化，透视问题的本质．高三解题教学不能仅停留在把题目解对而匆匆“滑过”，应更进一步，及时组织学生改编已做题目，以解决的问题为载体，实现试题增值，掌握思维之道．

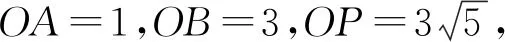
设计意图去掉圆方程与点坐标，减少或隐藏“解析几何味”，更倾向于解斜三角形问题．

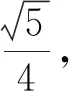
设计意图变换条件与结论，变向考查，考查的方向在圆的方程与性质．

改编3已知A(-1,0),B(3,0)，⊙O:x2+y2=r2(其中r>0)上有且仅有一个点P满足∠APB=30°，求r的值．

设计意图改变条件与所求结论，变最值为定值，旨在通过文字语言的暗示(有且仅有一个点)，寻找隐藏的圆，指向考查圆与圆的位置关系．

改编4已知△ABC，AB=4，∠ACB=30°，求AC的最大值．

设计意图以三角形为载体，可直接运用关于AB与AC的正弦定理，结合三角函数的有界性(sinB的最大值为1)，便可解决问题．也可基于正弦定理联想△ABC的外接圆，即动点C在以AB为弦的圆的一段优弧上，将AC视为△ABC的外接圆的一条弦，弦的最大值即为直径．

改编5已知△ABC，∠BAC=90°，AB=4，AC=6,P为△ABC内一点，且∠APB=135°，求CP的最小值．

设计意图条件中包含定弦所对定角，定角由锐角变钝角，动点P在以AB为弦的圆的一段劣弧上．旨在考查解析法，建系设点，目标转化为定点C到圆弧上动点P的最小距离，也即定点C到圆心距离减去半径．

5 思高三复习，练思维方式

在高三数学复习课中，教师究竟要教给学生什么？爱因斯坦曾说：“教育的目的不是学会知识，而是习得一种思维方式．教育的价值，不是学习很多事实，而是训练大脑去思考．”高三数学的复习课应基于数学学科特点，精选典型试题帮助学生跳出题海，重在教学生学会思考，优化学生的思维品质．一般来说，数学解题既没有固定的程序可循，也没有既定的模式套用，更多的是依靠对数学问题的透彻理解和对问题本质的深刻认识[2]．解题教学不仅是告诉正确答案，也不只是提供多种解法，而应体现学生的主体参与，暴露学生的思维过程，带领学生用数学的眼光观察题目、分析问题、理解本质，发展学生的认识力，让学生学会思考，提升数学学习力．