“双等腰模型”让建系法如虎添翼
宓武跃, 黄学文
(1.逍林中学,浙江 慈溪 315300;2.慈中书院,浙江 慈溪 315300)
立体几何作为数学高考大题“五常之一”,地位极其重要.传统法解立体几何题需要较强的空间立体感;而建系法解立体几何题“只要建系成功,一旦点坐标到位,后面就不是问题”.因此,建系法深受教师和学生的喜爱.除了传统建系、“暴力”建系外,笔者结合平时教学,推荐一种模型辅助建系,不妨称为“双等腰模型”.
1 模型及性质
如图1,两个等腰△ABC和△DBC,△ABC沿着BC翻折成三棱锥P-BCD.如图2,O为BC的中点,PB=PC,DB=DC,记OP=r,∠POD=θ,OA=OE,且点P在面BCD的上方,则有如下3个性质:
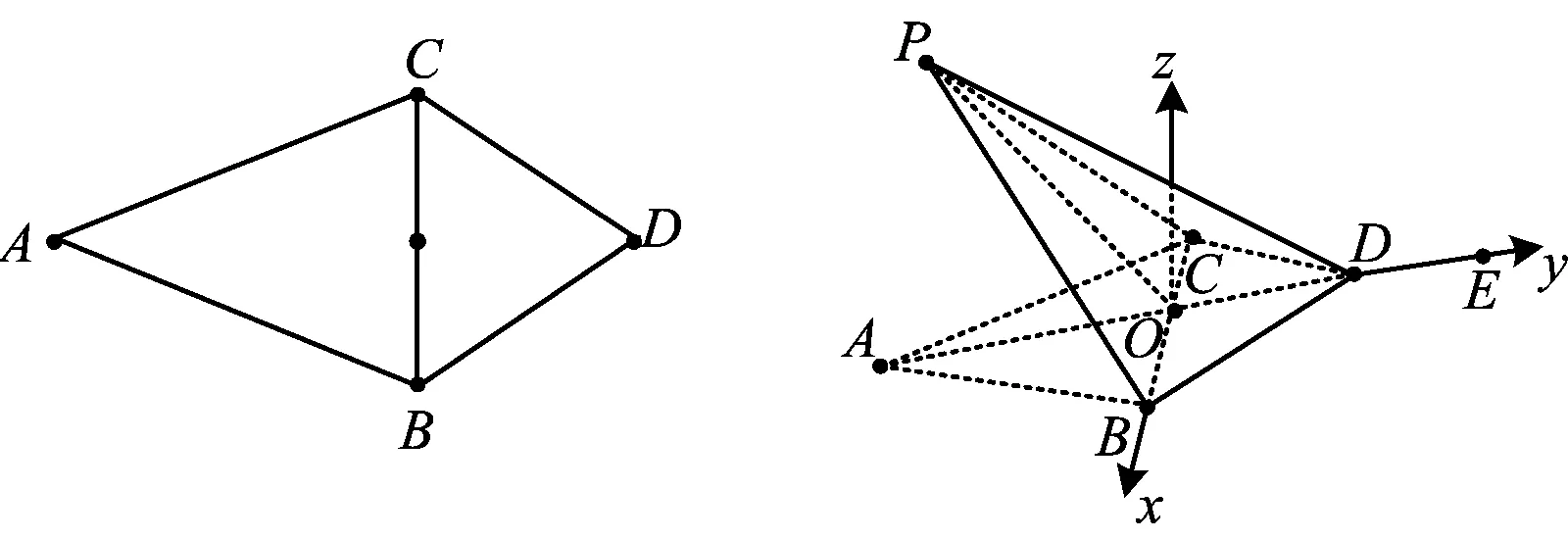
图1 图2
1)BC⊥OP,BC⊥OD,BC⊥面POD[1];
2)无论怎样翻折,点P始终在平面zOy内,且在底面的投影始终在线段AE上;
3)无论怎样翻折,∠POD始终是二面角P-BC-D的平面角,且点P的坐标为(0,rcosθ,rsinθ).
2 小试身手
例1如图3,在三棱锥P-ABC中,AB=BC=2,AP=PC,∠ABC=60°,AP⊥PC.
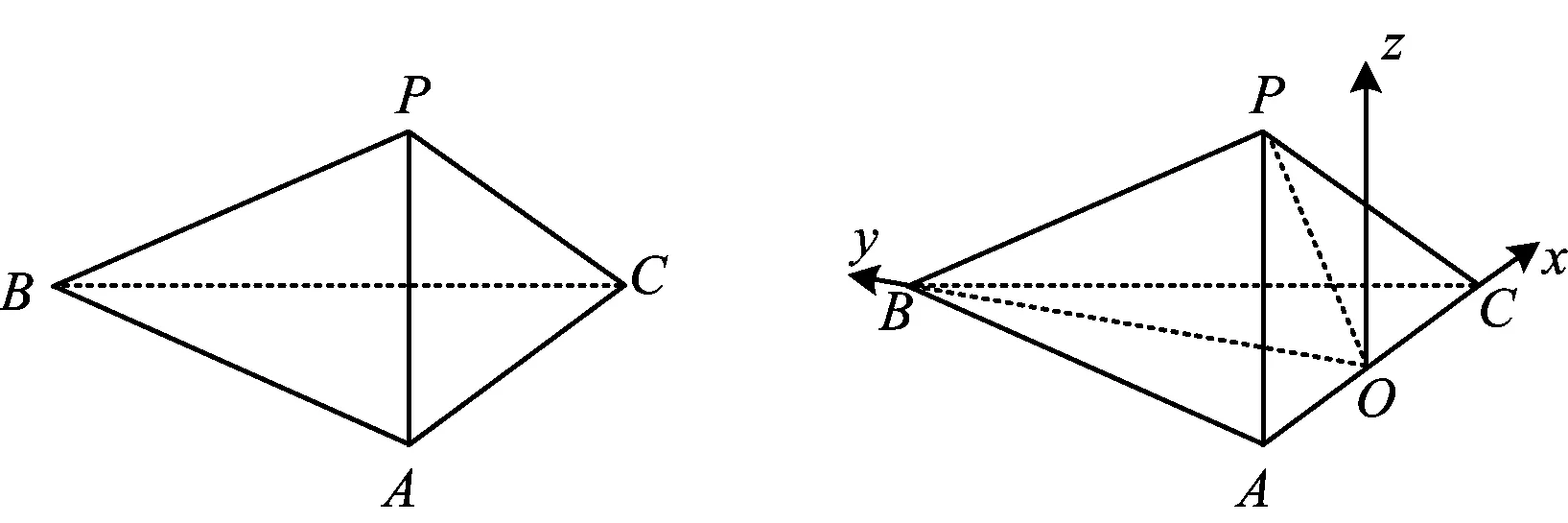
图3 图4
1)求证:AC⊥BP;
2)若直线BP与平面ABC成30°角,求BP.
分析根据主干条件,本题符合双等腰模型,等腰Rt△PAC和等边△BAC沿着AC翻折,且翻折程度不确定(点P为动点);加上第2)小题中的条件后,翻折程度才确定(点P为定点).
1)证明如图4,取AC的中点O,联结OP,OB.因为PA=PC,所以
AC⊥OP,
同理可得
AC⊥OB.
又OP∩OB=O,从而
AC⊥面OPB,
于是
AC⊥PB.
2)解由AC⊥面OPB知可建立如图4所示的空间直角坐标系.因为AB=BC=2,∠ABC=60°,所以
又AP=PC,AP⊥PC,从而
OP=1.
令∠POB=θ,则
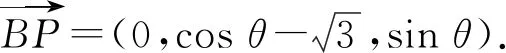
取面ABC的法向量n=(0,0,1),得
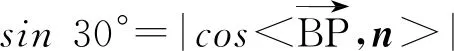
解得
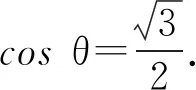
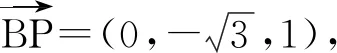
BP=2;
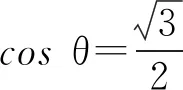
BP=1.
3 模型拓展
如图5,OA⊥BC,OD⊥BC,OA沿着BC翻折成空间几何体(如图6),始终保持OP⊥BC.记OP=r,∠POD=θ,OA=OE,且点P在面BCD的上方,则有以下3个性质:
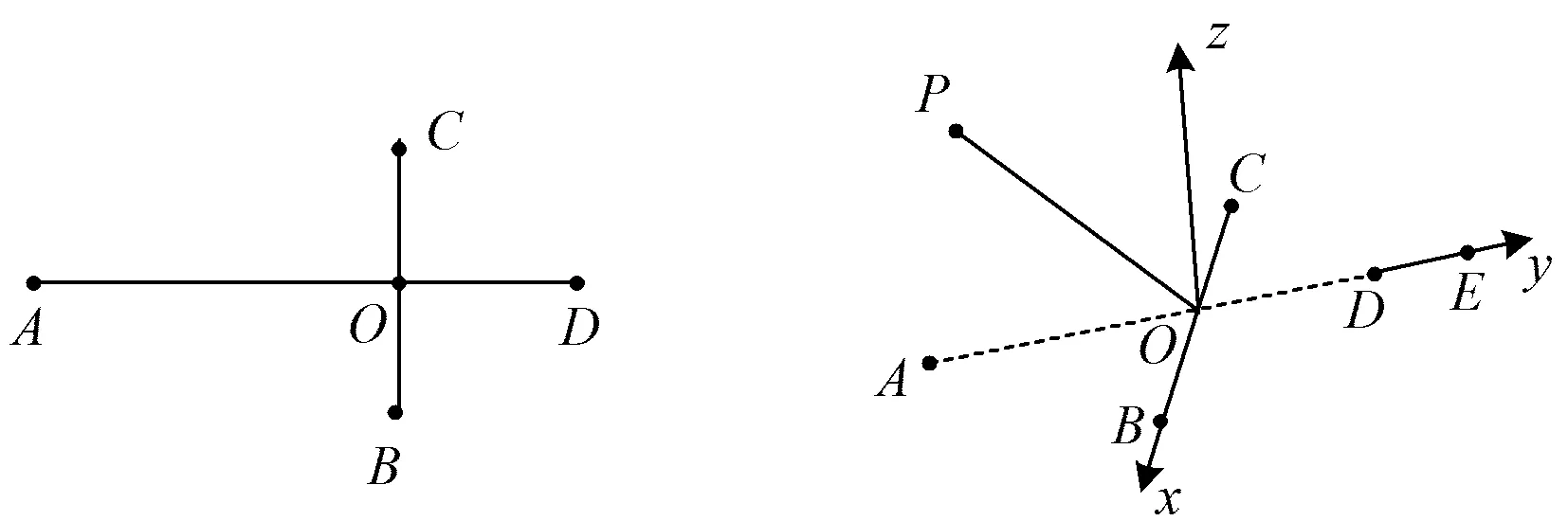
图5 图6
1)BC⊥OP,BC⊥OD,BC⊥面POD;
2)无论怎样翻折,点P始终在平面zOy内,且在底面的投影始终在线段AE上;
3)无论怎样翻折,∠POD始终是二面角P-BC-D的平面角,且点P的坐标为(0,rcosθ,rsinθ).
我们不妨把这种两个面内分别有直线垂直于交线且垂足为同一点的模型也称为“双等腰模型”.
例2如图7,在三棱锥P-ABC中,PA=PB=PC=5,BC=2AC=4,∠ACB=90°,点M在线段BC上,且3BM=5MC.
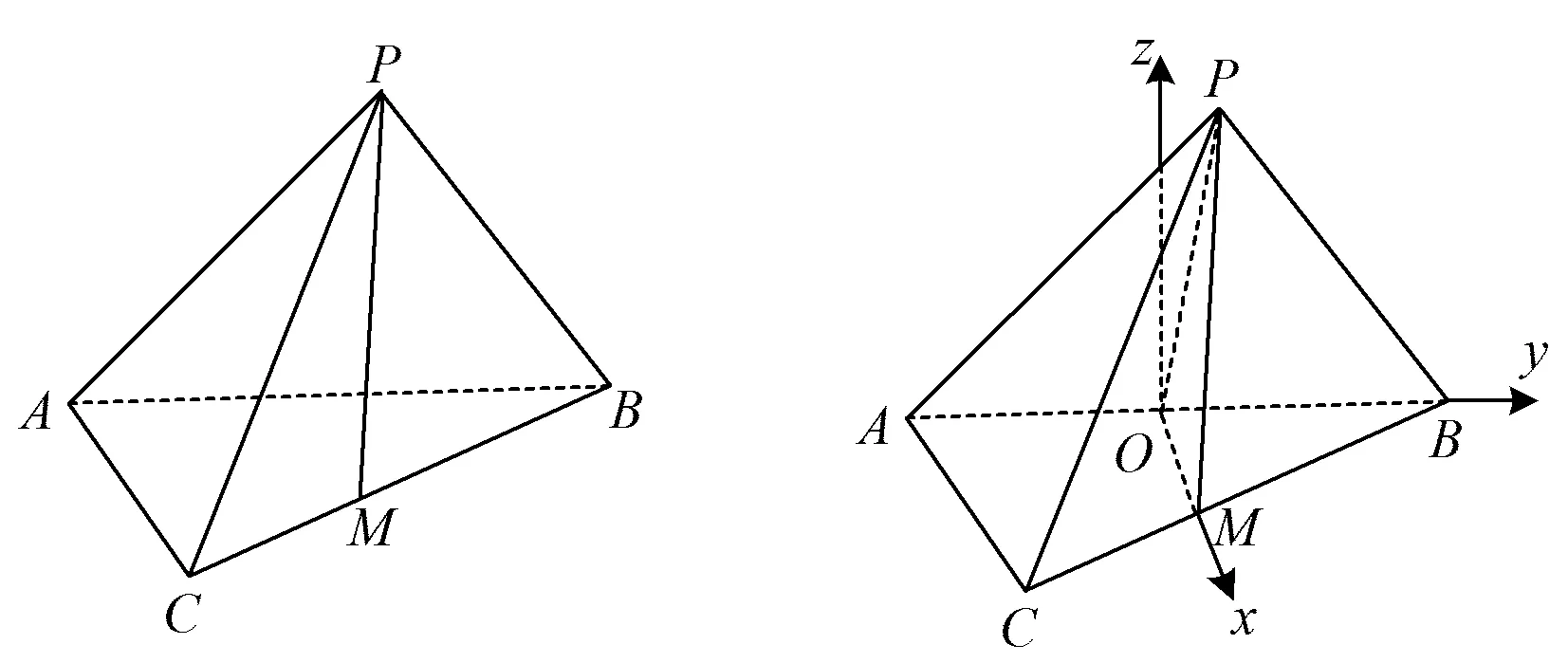
图7 图8
1)求证:AB⊥PM;
2)求二面角P-AC-B的平面角的余弦值.
分析如图8取AB的中点O,由PA=PB知PO⊥AB.要证AB⊥PM,只需证AB⊥OM即可,用相似可证.若PO⊥AB,OM⊥AB,本题符合双等腰模型,且PC=5,则翻折程度是确定的.
1)证明如图8,取AB的中点O,联结PO,OM.因为PA=PB,所以
PO⊥AB.
由BC=2AC=4,∠ACB=90°,知
又3BM=5MC,从而
于是
进而
△BOM=△BCA=90°,
得
∠BOM=∠BCA=90°,
即
AB⊥OM.
由PO∩OM=O,知
AB⊥面POM,
故
AB⊥PM.
2)解作Oz⊥面ABC,如图8建立空间直角坐标系,则
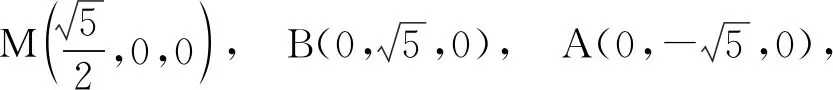
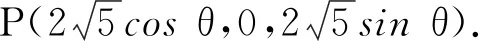
知

=5,
解得
cosθ=0, sinθ=1,
于是
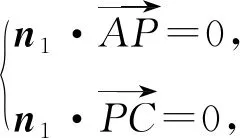
n1=(1,-2,1).
另取平面ABC的一个法向量n2=(0,0,1),得
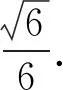
评注用建系法解立体几何题,只要建系成功,一旦点坐标到位,后面就是公式和运算的问题.双等腰模型为我们建系提供了方向,只需求出对应的r和θ,就能破解非底面上的点的坐标.
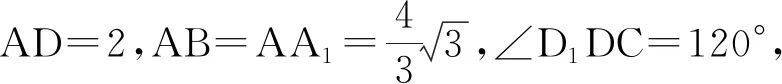
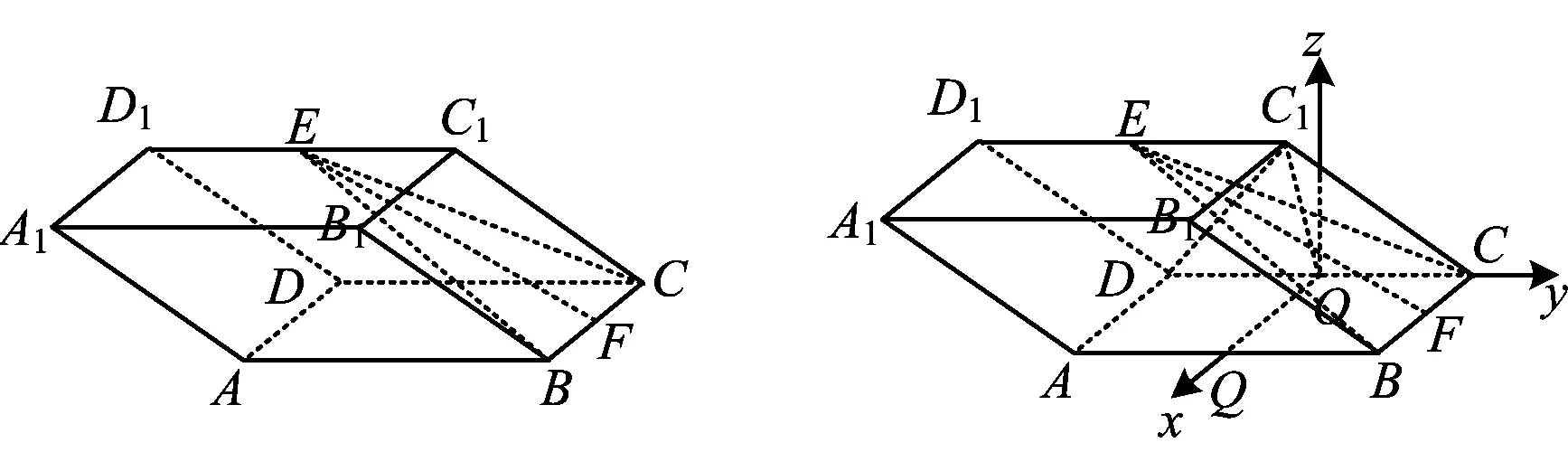
图9 图10
1)求证:AD⊥EF;
2)求DD1与平面BCE所成角的正弦值.
(2021年浙江省嘉兴市高三第二次数学模拟试题第19题)
分析如图10,第一步,发现双等腰模型C1O⊥CD,QO⊥CD;
第二步,利用双等腰模型建系;
第三步,定r=C1O=2,求θ=∠C1OQ=60°,破解点C1的坐标(rcosθ,0,rsinθ).
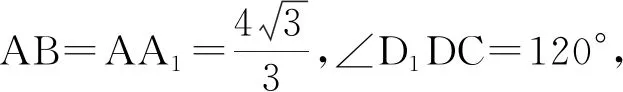
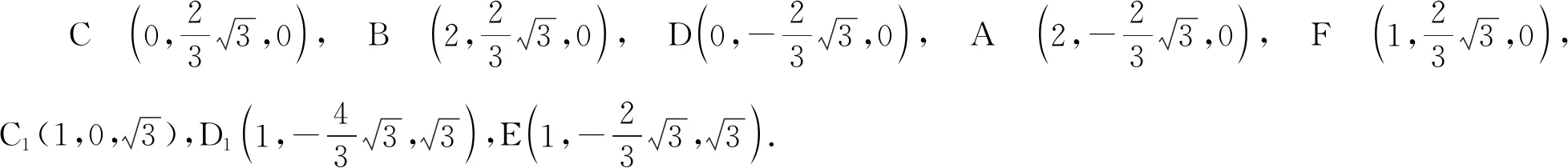
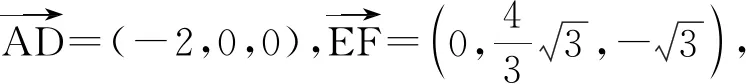
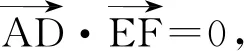
故
AD⊥EF.
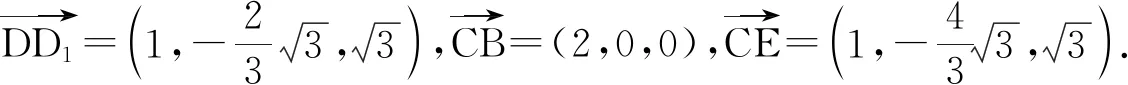
4 实战演练
例4如图11,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F-DC-B的平面角为60°.设M,N分别为AE,BC的中点,

图11
1)证明:FN⊥AD;
2)求直线BM与平面ADE所成角的正弦值.
(2022年浙江省数学高考试题第19题)
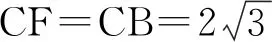
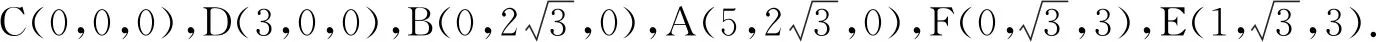
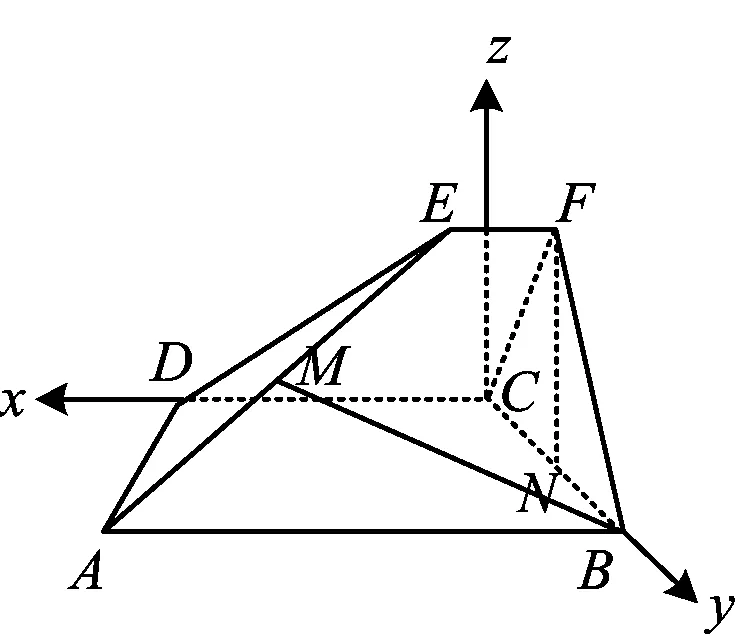
图12
因为N是BC的中点,所以
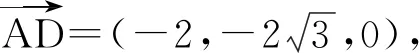
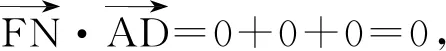
故
FN⊥AD.
2)解因为M是AE的中点,所以
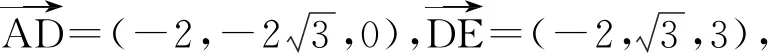
设BM与平面ADE所成的角为θ,得

结语在高中立体几何中,模型教学的几何直观性有着很强的指导意义,同时,模型教学也是提升学生数学学科核心素养的一个重要途径.学会剥离复杂图形,掌握双等腰三角形基本解题模型,那么遇到这类问题就能得心应手,解题也就水到渠成了[2].

