基于学科大概念的数学探究活动设计
——以“共轭”大概念为例
吴京霖, 丁祥芝, 王宽明
(贵州师范大学数学科学学院,贵州 贵阳 550025)
1 问题提出
“共轭”在高中数学教材中首现于“复数的概念”一节,教材中通过例题给出的共轭复数,计算两个互为共轭复数的模长后,给出了共轭复数的定义,在思考栏目中提出“两个互为共轭的复数在复平面中呈现什么样的关系”.对共轭复数的考查也局限在了共轭复数的定义、互为共轭复数的模长和几何特征上.在教学实践中,学生往往能很快理解上述知识点,亦对为什么具备这样特征的复数叫做共轭复数、高中数学中哪些含有“共轭”这一特征的问题则表现出强烈的好奇心.究其原因,在于“共轭”一词不像其他关系(如相等关系、相反关系、不等关系)那么直接明了,学生直接理解共轭存在一定的知识障碍.事实上,“共轭”作为一种现实世界的基本规律,具有丰富的内涵,在数学、化学、物理等自然学科中均有以“共轭”命名的概念[1].在高中阶段,数学教材中虽未给出明确定义,但广泛应用到的还有共轭根式、共轭双曲线等知识;在进入大学学习后,会陆续接触到诸如“共轭矩阵”“共轭梯度法”等.因此,学生深刻理解共轭不仅有利于通过“共轭”统领不同知识、形成联系,也为后续高等数学的学习打下坚实的基础.
“共轭”是对客观世界中物质形式的高度抽象,在高中数学中亦是联系诸多知识点的暗线,符合学科大概念的特征.所谓学科大概念是指用于使课程内容结构化、统领不同知识的核心概念或思想方法[2].“共轭”作为学科大概念,《普通高中数学课程标准(2017年版)》(以下简称《课标》)中并未明确要求掌握,不宜作为课时教学的素材.由于“共轭”命名的怪异,且内涵丰富,正是学生进行数学探究的绝佳材料,让学生在探究的过程中接受数学文化的洗礼,思考数学知识的本质与联系,发展学生的数学学科核心素养.
2 数学探究活动概述
数学探究活动是《课标》明确提出的五大学习主题之一.具体而言,数学探究活动是围绕某个具体的数学问题,开展自主探究、合作研究并最终解决问题的过程.具体表现为:发现和提出有意义的数学问题,猜测合理的数学结论,提出解决问题的思路和方案,通过自主探索、合作研究论证数学结论.通过数学探究活动,学生经历知识的产生、发展和运用的探索过程,发现数学知识的本质,培养学生发现问题、提出问题、分析问题和解决问题的能力,发展学生的数学学科核心素养.
3 “共轭”大概念探究活动设计
基于学科大概念的数学探究活动,其目的是让学生以学科大概念为统领,对数学知识进行结构化编码,形成知识间的联系,发展学生的数学学科核心素养.因此基于“共轭”大概念的数学探究活动设计可以分为4个步骤:“共轭”大概念的知识分析、设计探究活动、确定活动要求、探究成果评价.
3.1 “共轭”大概念的知识分析
3.1.1 “共轭”的来源
根据《新华字典》的解释,“轭”的含义为“驾车时搁在牛马颈上的曲木”.车轭是中国古代的一种驾车工具,此外,“轭”字还有“束缚”“控制”之意,如谭嗣同《仁学界说二十七界说》中提到:“君以名桎臣,官以名轭民,父以名压子.”由此可见,“共轭”一词体现的是一种“共同”“束缚”的特征.考虑到我国复数的发展主要源于明清时期对国外传教士所带的数学文稿翻译而来,为弄清“共轭”的具体含义,还需考虑共轭的英文含义.共轭的英文为conjugate,查阅《柯林斯英汉双解学习词典》发现,“con”意为“共同的”,“jugate”意为“成对的”“并排的”,因此conjugate一词主要体现的是“共同的、成对的”特征.所谓“共同的”主要是指形式上相同,而“成对的”主要是指事物具有某种相对的结构,如“左”和“右”、“上”与“下”、“正”与“负”等.
总之,相互“共轭”的两个事物并非完全“相等”,而是存在某种相互制约和联系.为了体现这一特征,我国数学家进行了巧妙的联想,用“共轭”来呈现这一特点.但是随着国家经济的发展,车轭这一个工具在实际生活中很少看到,这也造成了学生在理解“共轭”上存在一定的困难.
3.1.2 “共轭”性质探微
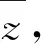
性质1乘积关系:(A+B)(A-B)=M2-N2.
性质2加法关系:M+N=2A,M-N=2B.
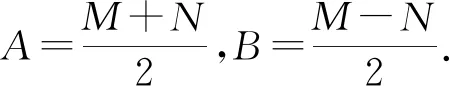
3.1.3 “共轭”性质的应用
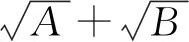
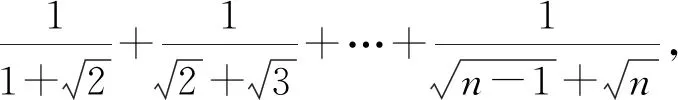
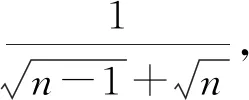
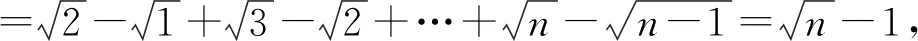
2)共轭复数.共轭复数的应用主要有两个,一个是复数除法中的分母实数化,另一个是复数的模运算.由于i的特殊性,因此共轭复数的性质1在形式上存在一定的区别.
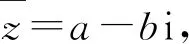
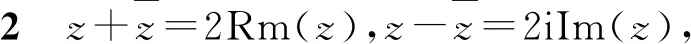

分析根据共轭复数的运算性质,分子、分母同时乘以分母的共轭复数使得分母实数化,即
从而
|z|=1.
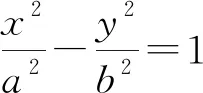
3.2 探究活动设计
基于对“共轭”大概念的知识分析,可以发现其命名起源于明清数学家对西方数学中的“conjugate”的意译,体现了我国传统文化中的数学元素,因此可设计第一个探究问题为“追根溯源,寻找共轭”,让学生通过网络、图书、报刊及访谈等方法,了解“共轭”一词的来龙去脉;通过形式的类比,发现其知识根源在于平方差公式,因此可设计第二个探究问题为“形式类比,发现本质”,让学生从共轭复数出发,观察其表达结构,发现共轭复数和平方差公式的本质联系;在明晰了共轭的含义和数学本质后,让学生类比数量关系中探究等式性质的方法,发现共轭的基本性质,因此第3个探究问题可以设计为“方法类比,探索性质”;最后在掌握性质的基础上,反考所学知识中具备“共轭”特征的数学知识,形成知识间的联系,因此第4个探究问题为“反考所学,发现共轭”.上述4个探究问题层层深入,让学生在探究的过程中,接受数学文化的熏陶,培养运用类比方式发现数学知识的思考方式,发展学生的数学学科核心素养.
3.3 活动要求
由于数学探究活动涉及信息收集与分析、知识分析、知识探索等过程,一个人难以完成,因此活动以小组为单位进行.如此做的好处不仅能实现育人价值,还能发展学生的合作交流能力.活动整体可分为“总—分—总”的形式,即:
1)以小组为单位讨论研究方案,落实每个成员的主要负责项目,形成具备可操作性的研究计划;
2)小组成员各自开展研究活动,并以专题作业的形式形成研究报告,交由小组长汇总;
3)小组成员内部交流各自研究收获,集体撰写小组数学小论文;
4)班级开展研究成果汇报,交流谈论,形成对“共轭”大概念的深刻认识.
3.4 探究成果评价
数学探究活动成果是学生们付出了辛勤的劳动和深入的思考汇聚而成的劳动成果,获得评价是学生满足“自我实现”需求的强烈心理倾向,一个好的评价不仅能提高学生对数学的学习兴趣,还能提高学生的自我效能感,获得学好数学的自信心[3].因此教师对于探究成果的评价应以积极评价为主,注重过程性评价,多维度评价学生在整个探究活动中的优秀之处.具体而言可以采用“个人—小组—班级”三级对象评价模式,针对个人的评价主要从探究行为、探究方法、探究态度中发掘学生的亮点,激发学生对数学探究的热情;小组评价则以小组活动计划、交流与合作、研究成果等宏观方面加以评价,发展学生的团队意识和集体荣誉感;班级评价则以整体表现做出宏观的积极性评价,亦需适当指出其不足之处,期待下次探究活动中能有更好的表现.此外,亦可开展学生互评,如通过学生投票,选出最佳小组、探究之星等,由于结果来自于学生,因此得奖的小组可以获得极大的成就感,而不得奖的小组亦不会有太大的挫折感,而是将目标放在下次探究活动中,期待获得更好的成绩.
4 结语
研究从数学大概念的角度设计了基于“共轭”大概念的数学探究活动,由于活动的目的在于以“共轭”大概念组织知识,故与一般的“发现问题—猜想问题—验证问题—应用结论”[4]探究过程不同,而是采用“追根溯源—寻找本质—演绎性质—反考所学”这样极具学科大概念特色的探究活动,如此设计的好处在于学生不仅可以对知识有更加本质的理解,同时还能将不同的知识点用“学科大概念”加以统领,提高学生运用知识的灵活性.基于数学大概念的数学探究活动,不仅可以在探究的过程中培养学生信息收集、发现知识、合作交流等能力,还能让学生经历用数学的眼光观察世界、数学的思维思考世界、数学的语言表达世界的过程,发展学生的数学学科核心素养,培养学生寻根问底、孜孜不倦的科学态度和理性精神.

