初中数学教材“平均数”比较研究
——以浙教版、人教版和北师大版为例
徐 羽
(浙江体育职业技术学院,浙江 杭州 311231)
《义务教育数学课程标准(2022年版)》(以下简称《新课标》)提出:数学教材为学生的数学学习活动提供了学习主题、知识结构和基本线索,是实现数学课程目标、实施数学教学的重要资源[1].用好教材,体现核心素养培养要求应当成为一线教师的自觉行动.
1 比较研究的目的
教材引领教师教学,对学生学习影响重大.本文通过对3个版本教材内容进行比较、结构分析,结合问卷调查,对浙教版教材的使用提出建议,希望为日常教学实践提供参考,从而提升教材使用质量.
2 比较对象和研究方法
本文选取了人民教育出版社出版的义务教育教科书《数学》以及北京师范大学出版社出版和浙江教育出版社出版的同名教科书(以下分别简称人教版、北师大版、浙教版),以3套教材中“平均数”章节为比较对象,从章节分布、课时设置、前言及活动设计、例题及正文、习题、旁白、插图等方面进行了比较研究.主要采用文献研究法、比较分析法、问卷调查法等方法进行定性、定量的比较分析.
3 比较研究内容
3.1 章节分布及课时安排
3套教材中“平均数”章节分布及课时安排如表1所示:
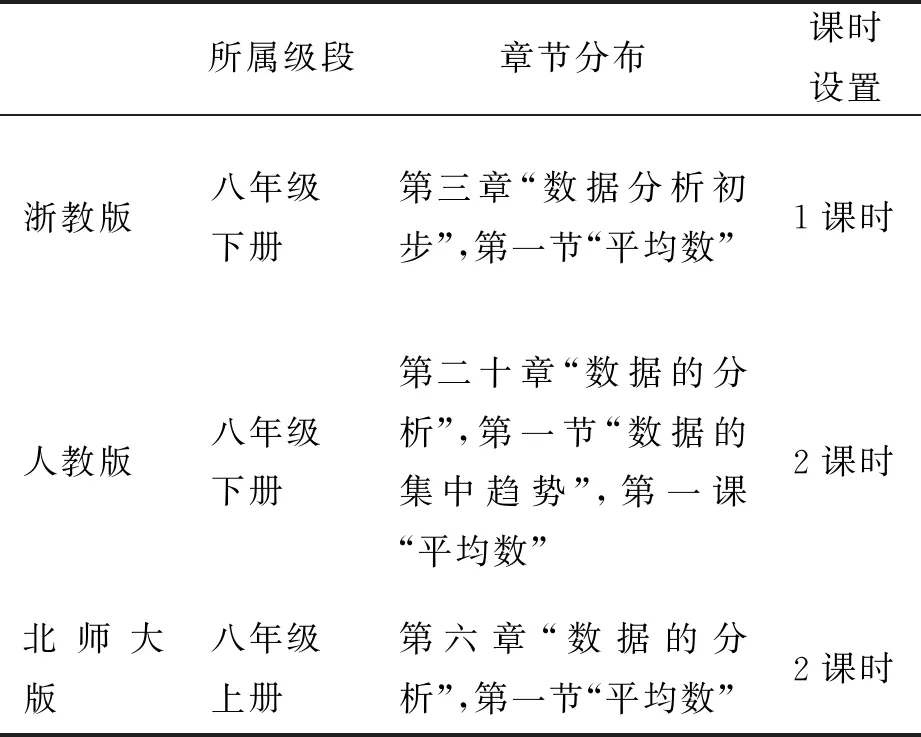
表1 章节分布及课时安排
3.2 前言及活动设计
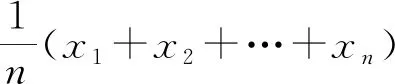
北师大版与浙教版结构几乎一致,以计算球队平均身高及年龄为引题,引入了平均数的新记法,并以小明的算式为例要求学生思考小明计算方法的合理性,为加权平均数的学习做好铺垫.
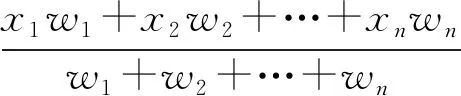
3.3 例题及正文
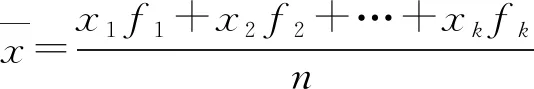
北师大版与浙教版在正文编排上相似,通过例题解析给出了加权平均数的释义,但都没有给出更为一般的表达式.相比其他两版,北师大版教材更注重培养学生理论联系实际的能力,正文两次提出由学生自己联系实际设计方案及相互交流.此外,3个版本教材中唯有北师大版提及物理学中的平均速度问题,而且要求学生从“权”的角度跨学科理解问题.
浙教版是唯一没有在课本中提及计算器的版本,无论是计算器计算平均数的使用说明(如人教版)或是提示复杂问题借助计算器计算(如北师大版).
3.4 教材习题比较
3个版本教材的课后习题配置如表2所示:

表2 课后习题配置
3个版本教材的课后习题背景如表3所示:

表3 课后习题背景
3个版本教材课后习题总体水平均衡,问题难度梯度设置合理,关注全体学生的发展,有一定的数学文化价值.
关于加权平均数的练习浙教版比例最低,人教版最高,北师大版较为均衡,和3个版本教材主体内容编排比例基本一致,题量也和课时安排对应.
3个版本教材均选取了学生日常较为熟悉或者容易理解的主题,配置合理丰富.其中各种成绩的问题出现频率最高,总共出现6次.人教版气温问题出现两次,北师大版身高问题出现两次.人教版及北师大版均有农业背景问题出现,浙教版练习题中没有出现(正文内容中有),但是出现了两次涉及环保的主题(快餐盒、塑料袋).
说明人教版的对应习题一组,置于20.1.2“中位数和众数”之后.北师大版练习题为两组:习题6.1和习题6.2.
3.5 插图及旁白
浙教版为引言和例2配置了插图,没有出现旁白.果实累累的果园照片和排列整齐服装一致的学生照片完全符合问题的背景,也侧面反映了国家欣欣向荣和人民积极向上的精神风貌.浙教版是3个版本中唯一使用实景照片作为插图的.
人教版插图1出现在引题后的加权平均数定义处,插图给出了“权”的英文表述及解释.插图2对数据分组后的“小组中的组中值”做了详细释义.两幅插图形式一致,放在问题中,醒目且自然.该教材旁白1为启发学生思考“权”的作用,旁白2则是提问全面调查法是否适合考查灯泡的平均寿命,这既兼顾了新授知识的启发也回顾了之前数据调查的内容.
北师大版没有出现插图,旁白有两处:第一处为算术平均数定义给出后提示勿忘使用计算器处理复杂计算;第二处为例题中提问两次结果不同说明了什么[4].
总体看,3个版本教材对插图及旁白都处理娴熟,有画龙点睛之妙,也让学生看着亲切自然.
4 内容总体评价
“理解平均数的意义,能计算加权平均数,知道它们是对数据集中趋势的描述”,这是《新课标》提出的内容要求.在随后的学业要求中,《新课标》也指出:能计算一组数据的中位数、众数、加权平均数,知道计算加权平均数的分布式计算方法,知道中位数、众数、平均数都能刻画这组数据的集中趋势以及它们的各自特点[1].
总体来说,3个版本教材中素材选取均贴近学生现实,显得真实可信.教材正文注重来龙去脉,注重发展学生的素养,有利于教师引导,使用得当.3个版本教材均能有助于教师达成《新课标》所提的学业目标.同比之下,浙教版教材体现出的教学要求略低于其他两版.
5 浙江部分学校问卷测试结果及对教学的建议
5.1 浙江学生新授“平均数”后问卷及测试中所反映的问题
笔者在浙江几所中学进行了问卷调查及测试分析,学生在本节内容的学习上有以下4个问题较为普遍:
1)课本前段主要讲述了算术平均数,课后也有大量习题是关于算术平均数计算的.但是这部分内容学生在小学阶段均已熟练掌握,课后习题在学习该章节之前也能应对.调查反映30%的学生表示在章节学习之后不觉得自己对算术平均数的认识有所提高.
2)在解决例1之后提出了加权平均数的概念,但是没有给出明确的定义或者计算公式.近50%的学生表示对“‘权’从何而来,又有哪些表现形式”模糊不清.
3)该内容新授课后的调查表明:近50%的学生认为加权平均数是算术平均数的简便算法.少数学生不理解为什么有的时候“权”可以改变(如课本例2),有的时候“权”却是固定不变的(如课本例1).
4)测试表明:70%的学生在学习该章节之后,不能将加权平均数迁移至物理当中的速度、压强等知识中.90%的学生在面对由频数分布表求加权平均数的问题时,表示没把握解决.
5.2 浙教版教材使用的教学建议
1)增加该课课时,由1课时增至2课时.
课堂教学是学生学习的主渠道.课堂的知识性、思想性是课后学习无法比拟的.教学参考建议对该章节分配6课时,其中复习、评价、机动使用占3课时.从课后的测试情况看,包含“算术平均数”和“加权平均数”两块内容的教学,仅仅1课时是不够的.
2)补充例题,帮助学生生成“权”的概念,突出教学重点.
教材没有采用复杂的字符定义加权平均数,而是主张学生经历加权平均数产生的过程,这一点上和北师大版教材一致.要理解“加权平均数”,把握“权”的概念是关键.可惜的是,浙教版的例1,“权”比较隐蔽,即使通过算式变形提炼出来,对学生而言,“权”的味道依旧不浓.调查中问题2)和问题3)的出现也反映出该问题,仅仅凭借教材例题,期盼学生领悟“权”的意义是不现实的.教师可以在教材之外适当补充例题,多角度地让学生感受“权”的生成,掌握“权”的概念.
3)总结加权平均数的一般表达式,帮助学生理解加权平均数的多种表达形式,扫除学生疑点.
经历了概念生成,教师可以引导学生主动提炼加权平均数的一般表达式,指明算术平均数是加权平均数的特殊情况.这对于学生理解以及应用加权平均数都能起到关键作用.参照人教版教材,加权平均数表现形式多样,多种表达式就是其多样性、灵活性的表现.对于“权越大,对平均数的影响就越大”,可以从直观感受和表达式计算这两个方面加以解释说明.
4)理论联系实际,发动学生讨论,进一步理解“权”的意义,突破教学难点.
在课堂上,教师应增加频数分布表、求加权平均数等问题,让学生了解在实际问题中“权”的各种处理方式,从而进一步理解“权”和加权平均数的意义.“权”在形式上是多样的,既可以是自发形成的,也可以是根据重要性人为设定的.统计特征数源自于生活,教师应当帮助学生选取实例,引导学生将知识运用到实际生活当中去.
5)增加设置跨学科问题,夯实应用支点.
跨学科的问题可以让学生开阔视野,走出数学“孤岛”.北师大版中的速度问题就是很好的启发.事实上,有关加权平均数在平均速度、平均压强、溶液浓度等科学类问题里的应用非常广泛.通过问题的分析适当引导学生进一步理解分散的数据可以有“权”,连续的变量也可以含“权”,加权平均数既可以描述离散的量,也可以用于描述连续的量.通过跨学科问题的解决,让学生进一步体会数学的学科价值,为后继知识的应用打下基础.
6 结语
《新课标》根据核心素养发展水平提出了“学业要求”,明确了“教到什么程度”.教师可以通过教材比较丰富课堂素材,完善课程理念.相信在进一步明确“教什么”“怎么教”之后,教师定能结合教材特点,提升教学效益,更好地发挥数学课堂的育人作用.

