循理入法 以理驭法——以“点到直线的距离公式”为例谈数学运算素养的培养

周建峰

(浙江师范大学附属中学，浙江 金华 321004)

中学数学教学一直重视数学运算能力的培养，从“双基”、数学“三大能力”到“四基”“四能”，再到六大核心素养，无不突出数学运算的重要性．《普通高中数学课程标准(2017年版)》提出6大数学核心素养，“数学运算”是其中之一，是在明晰运算对象的基础上，依据运算法则解决数学问题的素养，主要包括理解运算对象，掌握运算规则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等[1]．

在教学实际中，笔者发现：多数学生运算能力不强，学习中“看看会，算算不对”的现象屡见不鲜．究其原因，看似学生能力欠缺，但真正的根源在于教师，教师在教学中急功近利，偏重知识和方法，希望通过题海战术达到提升数学运算核心素养，而忽略了对算理的探究，没能在课堂上扎扎实实地开展运算教学．

数学运算的关键是对算理的探究和算法的设计，包括要算什么、可以怎么算、为什么这样算、实际操作、可不可以优化等．数学教材是数学课程实施的重要载体，人教版普通高中新课程《数学(选择性必修第一册)》第2．2．3节“点到直线的距离公式”较好地呈现了数学运算核心素养的培养蓝本．

1 新旧教材比较

新旧教材都重视对概念的理解，体现坐标法处理问题的思想，并设置“思考”引导教学进行更深层次的探究，用较为简洁的方法推导出点到直线的距离公式，但在解决问题的策略上存在明显的差异．

1.1 教材内容呈现的差异

旧教材设置了“思考”，从点到直线的距离的定义出发，引导学生思考如何求P0Q的长即点P0到直线l的距离，但教材中回避了用坐标法具体求解，采用面积法得到点到直线的距离公式．

新教材设置了“探究”，同样从点到直线的距离的定义出发，引导学生思考如何求P0Q的长即点P0到直线l的距离，详细地给出了通过坐标法得到点到直线的距离公式的求解过程，继而利用“思考”引导学生反思优化运算的方法．再用“探究”带领学生利用向量法，通过投影向量运算求出结果，体现了方法的多样性和向量的工具性．

1.2 教学处理的差异

1.2.1 解决问题的方式

旧教材提及从定义出发推导公式的自然思路，但由于具体运算需要一定的技巧没有呈现运算过程，虽设置“思考”：试一试，你能求出|P0Q|吗？但教师和学生都有排斥烦琐运算的正常心理，教材没有呈现，自然以为是不重视这种“常规思路”，那么教学实践中一般不会采用常规方法．教学中常见的处理方法有以下3种.

给定点P0(x0,y0)和直线l：Ax+By+C=0，先分析A=0和B=0这两种特殊情况，然后再分析一般情况：

方法1和教材一样采用面积法或者相似等方法.

方法3同新教材一样用常规思路，但只是为推导结果，不会深入探究改进运算方法．

使用以上3种处理方法时，往往都会回避复杂的运算过程，只呈现运算结果，用较长时间和较多例题在公式的应用上，强化记忆公式，忽视运算能力的培养．

而新教材不仅呈现了从定义出发推导公式的完整过程：基于定义所给定的几何要素，利用垂线求交点，再用两点间距离公式推导出点到直线的距离公式[2]．在此基础上设置“思考”,启发学生反思引起运算复杂的原因，附上一段文字说明引导学生发现简化运算的方法，从而巧妙解决问题．新教材的优点在于不仅强调处理问题的一般思路，还启迪学生寻找优化的方案，培养学生的创新能力，发展数学运算素养．

1.2.2 运算方法的选择

旧教材只用了坐标法推导公式，而新教材不仅采用坐标法，还提供了向量法．点到直线的距离公式的推导方法有很多，但究其本质进行归类主要还是以上两种，因此在教学时，要从思想方法的高度将学生的各种不同运算方法进行归类，这也是运算教学需要解决的问题．

1.3 侧重点的差异

从教材切入方法看，旧教材引导学生“思考”，侧重于“想”，新教材却引导学生“探究”，侧重于“操作”．

从知识和能力层面看，旧教材侧重于知识，即点到直线的距离公式，强调“双基”．而新教材通过经历点到直线的距离公式获得的过程，培养学生的数学运算能力，强调“四基、四能”．

从数学运算本身看，旧教材注重算理弱化算法，通过分析教材，使学生明白可以怎么算，但对于复杂的运算采用回避的办法.而新教材则算理和算法并重，通过算理理解算法，反之通过算法实现算理，发挥了良好的育人功能，启发学生深度思考.面对棘手的运算分析原因，探究改进方法，使学生“知其然，知其所以然”，还“知其何以使然”.此外,新教材还通过多元处理问题的方法，告诉我们数学运算素养不仅包括运算的能力，还包括运算方法的选择．

2 基于数学运算素养培养的教学过程设计

基于培养学生数学运算能力的教学，需要引导学生明晰算理、理解运算的依据，在获取算法和应用算法时应“知其然，且知其所以然”，引导学生认真剖析“获取正确运算结果的历程”，形成“范式”，以规范的数学语言将运算步骤程序化、数学化，并不断渗透运算技巧，探寻运算的“捷径”，使学生逐步养成优化算法的习惯[3]．

2.1 寻找算理——要算什么，可以怎么算

点P到直线l的距离，就是点P到直线l的垂线段PQ的长度，其中点Q是垂足(如图1)．

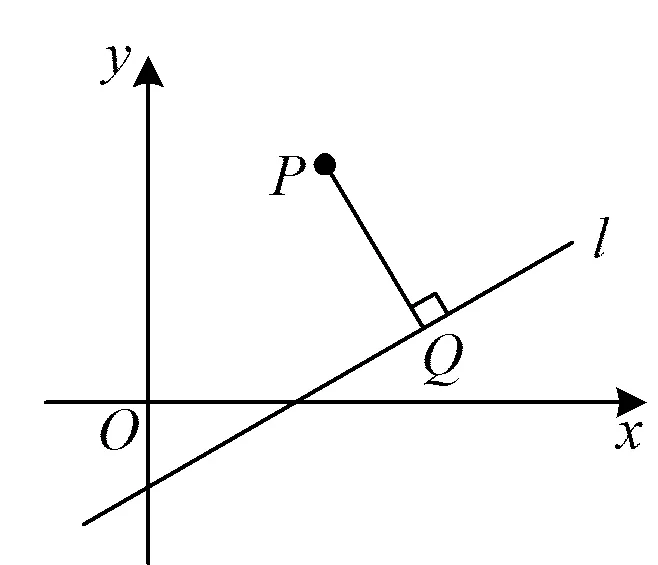
图1

求出垂足Q的坐标，利用两点间的距离公式求出|PQ|，即求得点P到直线l的距离．

2.2 设计算法——为什么这样算

已知条件是点P的坐标(x0,y0)和直线l的方程Ax+By+C=0，可以通过以下路径求得|PQ|(如图2)．

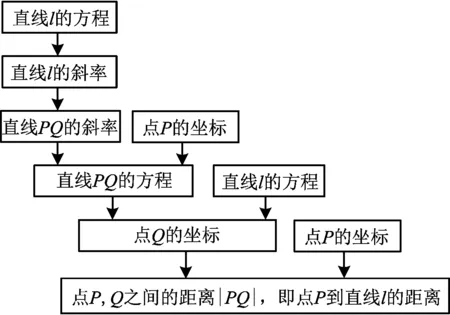
图2

2.3 实现算法——具体运算过程

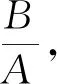
即

Bx-Ay=Bx0-Ay0.

解方程组

得到垂足Q的坐标为

从而 |PQ|

验证当A=0或B=0时，上式仍然成立．因此，点P(x0,y0)到直线l：Ax+By+C=0的距离为

这种求解方法利用坐标法，把几何关系转化为代数运算得以实现．

2.4 优化算法——可不可以优化

反思上述方法，由点到直线距离的定义，将点到直线的距离转化为平面上两点间的距离，思路自然，设计合理，但运算量较大，特别是其中求点Q的坐标和利用两点间距离公式求|PQ|过程中的化简，大多数学生很难单独完成．

针对以上两个计算中的难点，进一步思考有没有简化运算的方法．

思路1“设”的是什么？“求”的是什么？

从两点间距离公式求|PQ|的形式看，

能否不求出点Q的坐标，而直接求(x-x0)2+(y-y0)2？

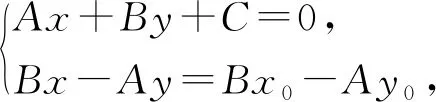
把x-x0,y-y0看成整体,得

(A2+B2)[(x-x0)2+(y-y0)2]=(Ax0+B+y0+C)2,

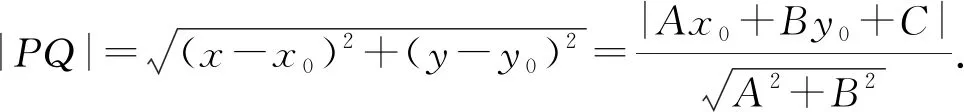
这里利用了设而不求的方法，循理入法，通过求(x-x0)2+(y-y0)2实现了问题求解，避免了复杂的运算．

思路2由PQ⊥l，可否构造直角三角形求解？

优化方法2设直线l与y轴的交点为R，联结PR.在Rt△PRQ中，利用勾股定理求出|PQ|(如图3)．

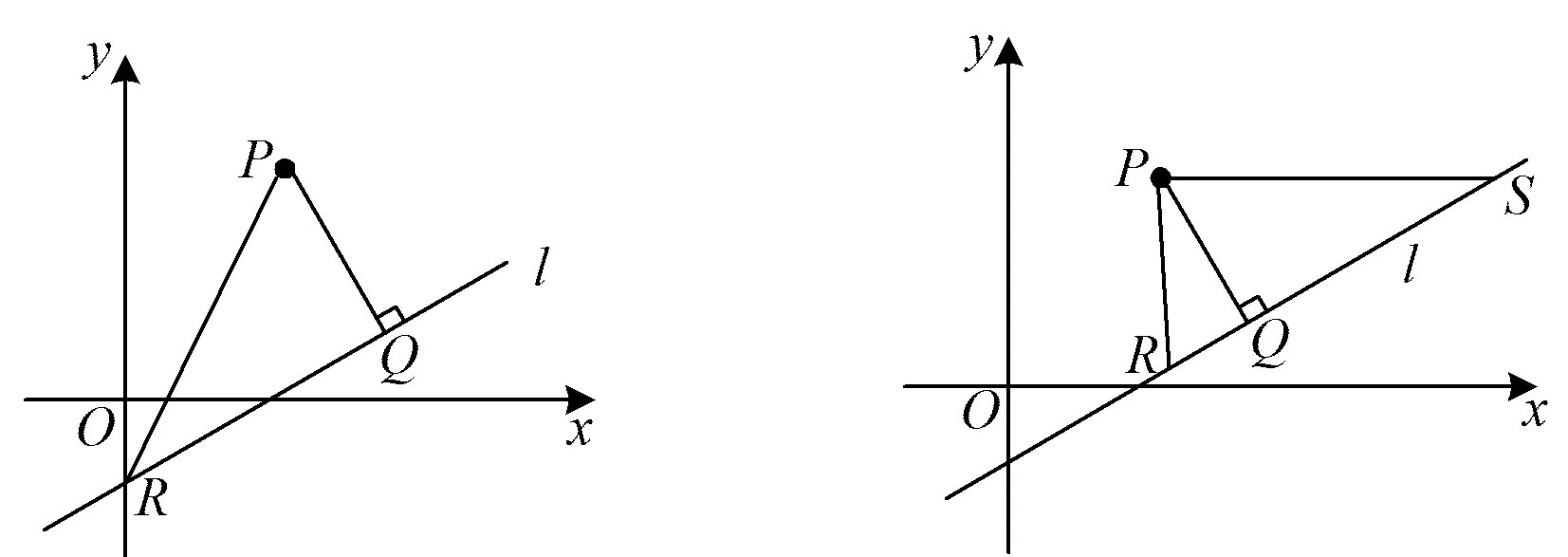
图3 图4

这个方法起点很低，利用了初中的知识，但在求解过程中，发现利用点A，B，C和x0,y0表示|QR|比较困难．

思路3垂线段长可以看成三角形的高，能否构造三角形通过面积法求解？

优化方法3如图4，过点P分别作x轴和y轴的平行线，交直线l于点S，R，则可求得

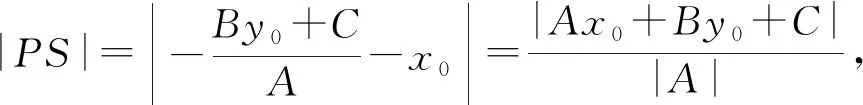
根据等面积法可得

思路还是构造三角形，但利用与坐标轴平行的线段降低了长度表示的难度，优化了运算的烦琐程度，以理驭法，这也是旧教材中选择的求解办法．

思路4通过前一章学习，我们知道，向量是解决距离和角度问题的有力工具，能否利用向量方法求得点到直线的距离呢？

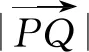
由向量知识可知n=(A,B)是与直线l的方向向量垂直的向量，则

通过投影向量，运用向量运算求解，既简化了运算，又拓宽了思考问题的思路，起到了异曲同工的效果．

3 结语

数学运算是数学活动的基本形式，在数学六大核心素养中占据基础性和工具性地位．数学运算素养的培养不可能一蹴而就，仅仅通过学生多做、死做、蛮做难以实现，需要教师在教学过程中有效利用载体，扎扎实实地进行数学活动，通过课堂师生双边活动，发挥学生的无限想象，探究计算方向，合理设计算理，通过反思不断优化算法，方可真正达到育人的目的，一展数学魅力！