辨析三类错解根源 提升逻辑推理能力

张 淦

(新昌中学，浙江 新昌 312500)

“学生的错题,教师的宝”.在教学活动过程中,虽然“错解”总是遭人讨厌,但是“错解”展现了学生的思维活动过程,是教师了解、掌握学情的重要途径.特别是一些“不露痕迹”的错解,洞悉错误之处需要学生具有良好的数学素养,需要学生对相关概念、关系、结构有明确的认识和理解,对解答过程中各步骤有清晰的逻辑分析,而不是“机械式”“无意义”地进行数学活动.

此类隐蔽性强的错解问题,是教师教学中的宝贵财富,正如皮亚杰所说:“错误是有意义的学习所必不可少的.”教师应当引导学生,辨析错解根源,吃透概念,理清对象间的关系,提升学生的逻辑推理能力.

1 必要不充分型错解——理清关系,抓住本质

必要不充分型是主要的错解类型,学生在解题过程中,弱化问题条件往往是导致错解的根源所在.

例1在锐角△ABC中,角A,B,C的对边分别为a,b,c,且sinB+sin(A-C)=cosC.

1)求角A的大小;

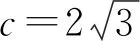
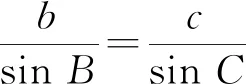
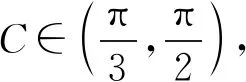
从而

a2+b2=2b2-6b+12∈(12,20).

解法2由余弦定理可得

a2=b2-6b+12.

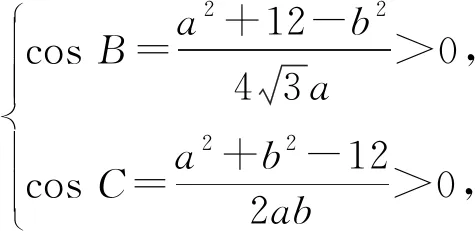
即

得b∈(3,4),从而

a2+b2=2b2-6b+12∈(12,20).

想不到的是,有学生非要让笔者看他的解答过程并抱怨道“知道自己的解答是错的,但是想了老半天,就是没发现哪一步有问题”.

错解由余弦定理可得

a2=b2-6b+12.

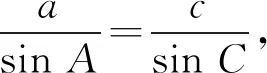
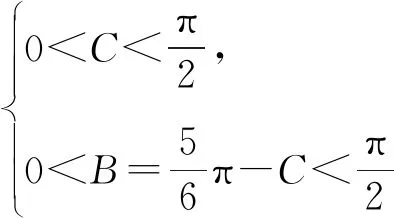
因为a2=b2-6b+12∈(3,4),所以

b∈(2,3)∪(3,4),

于是a2+b2=2b2-6b+12

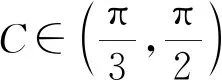
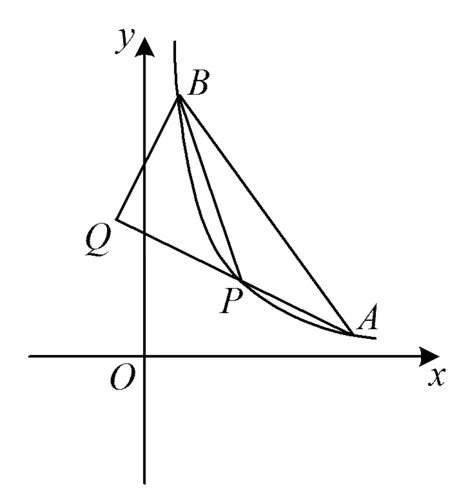
图1

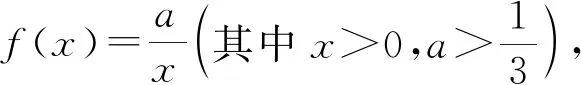
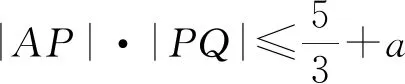
1)略.

错解2)由题意可知

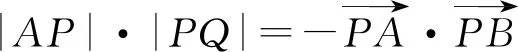
整理可得

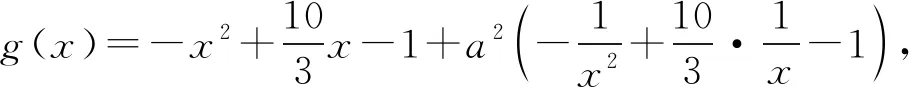
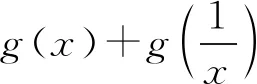
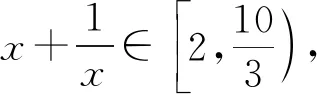
故只需

得

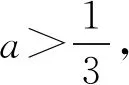
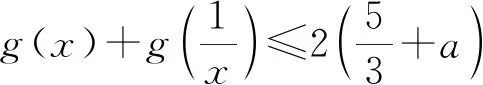
得

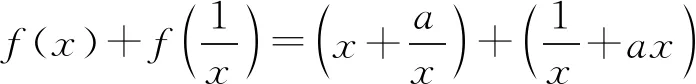
故二者不等价.因此,例2解法中存在瑕疵,需要进一步完善.

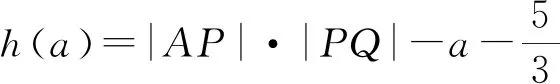
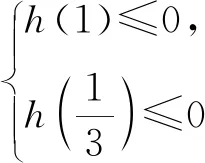
2 充分不必要型错解——实事求是,注重论据

充分不必要型是重要的错解类型,学生在解题过程中,由于对概念、定理、公式理解不清或受思维定势的影响,主观强加问题条件是这类错解的根源所在.

例3如图2,在多面体ABC-A1B1C1中,平面A1B1BA⊥平面ABC,平面A1B1C1∥平面ABC,∠A1B1C1=∠ABC=90°,四边形A1B1BA为正方形,B1C1=A1B1=2BC=2,E为棱A1B1的中点．

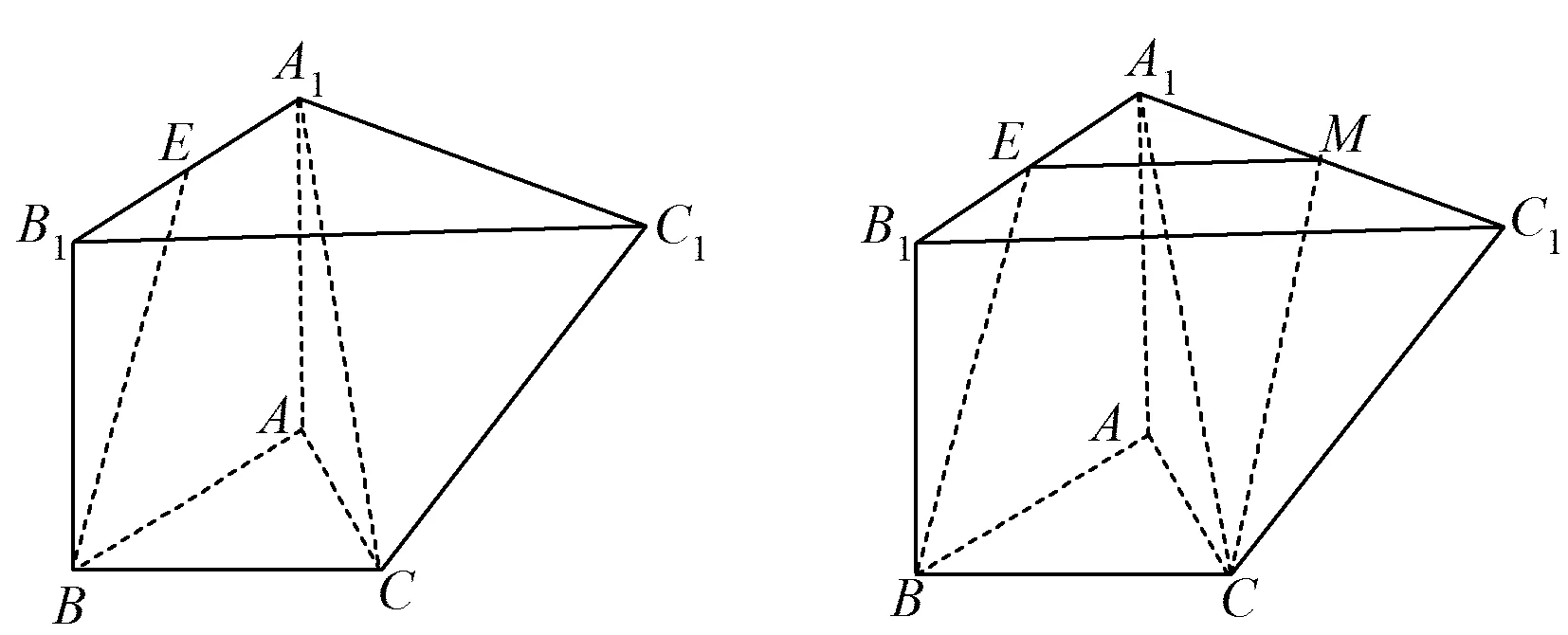
图2 图3

1)求证:BE∥平面A1CC1;

2)求直线A1C与平面A1AC1所成角的正弦值．

下面仅对第1)小题进行分析.

1)错证如图3，取A1C1的中点M,联结EM.因为点E,M为中点,所以

EM

又BC故四边形EMCB为平行四边形,BE∥MC.又因为BE⊄平面A1CC1,MC⊂平面A1CC1,所以BE∥平面A1CC1．

上述证法在学生的解答中普遍存在,然而在证明中,学生强加了“BC∥B1C1”这一条件.事实上,应先补充证明BC∥B1C1.因为平面A1B1BA⊥平面ABC,平面A1B1BA∩平面ABC=AB,且BC⊥平面ABC,所以BC⊥平面A1B1BA,同理可得B1C1⊥平面A1B1BA,于是BC∥B1C1.

例4如图4,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.

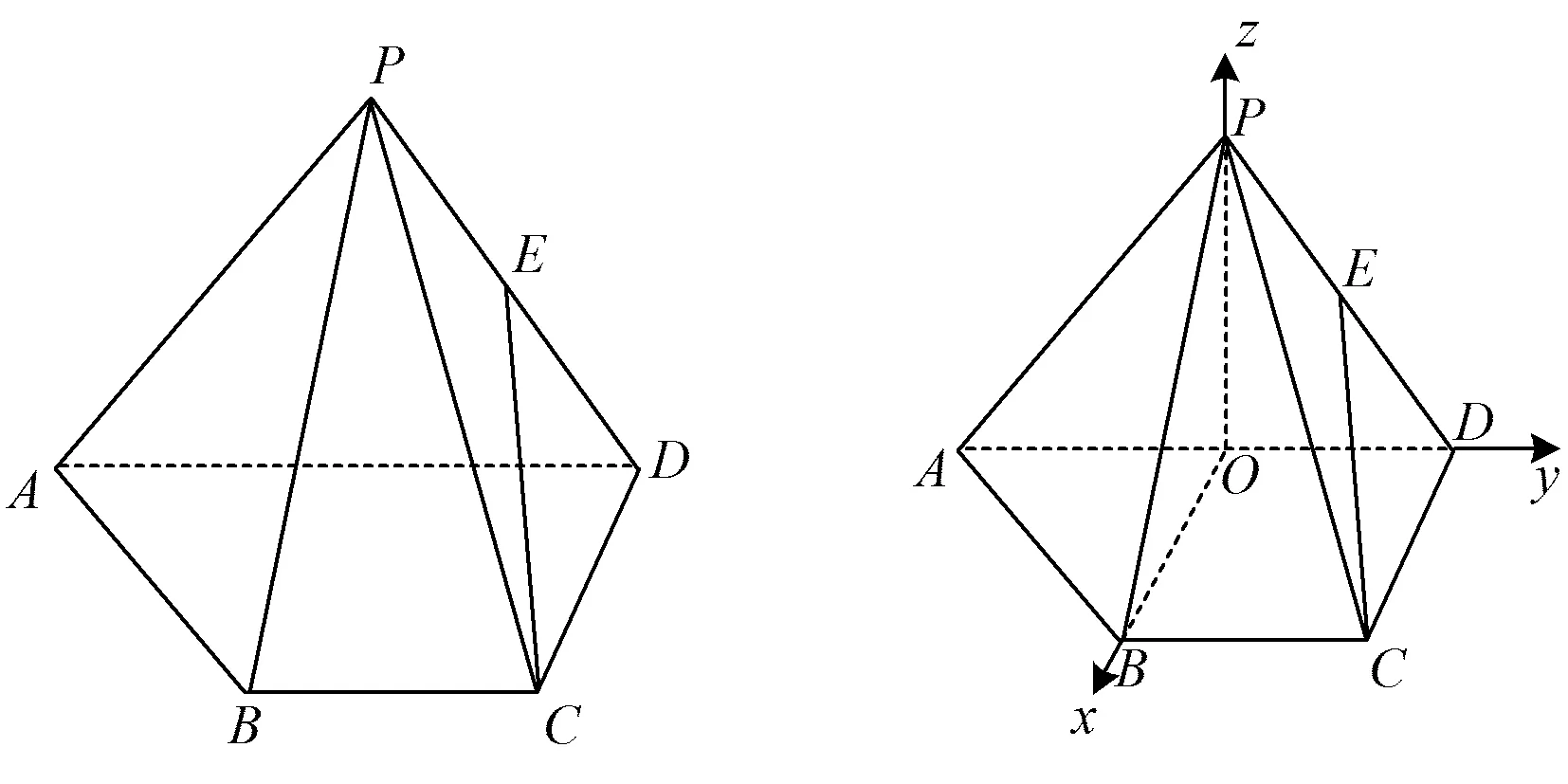
图4 图5

1)证明:CE∥平面PAB;

2)求直线CE与平面PBC所成角的正弦值.

(2017年浙江省数学高考试题第19题)

1)略.

2)错解如图5,以AD的中点为坐标原点O、分别以OB,OD,OP所在直线为x,y,z轴建立空间直角坐标系(解答过程略).

当年笔者有幸参加了阅卷工作,上述向量代数解法是典型的错误类型.学生空间感知能力不足,忽视点、线、面的位置关系,不经思辨论证,强行添加了平面PAD⊥平面ABCD这一条件是错解的根源.

3 既不充分也不必要型错解——大胆猜想,小心求证

既不充分也不必要型错解,往往是学生猜想答案引起的.事实上,学生通过不完全归纳法、类比法、简单枚举法、数据分析等或受一般数学观念影响,推断问题结果.究其实质,应该是归纳推理.

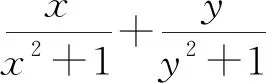
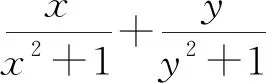
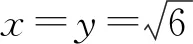
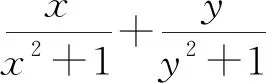
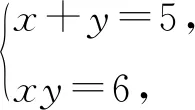
一般观念、个人直觉在数学结论发现的过程中具有重大作用,但是并不“保真”;严谨性的功能不在于发现知识,而在于解释知识[1].在数学教学活动过程中,教师应将演绎推理和逻辑推理能力培养并重,鼓励学生大胆求证、小心求证.

实际上,由xy=6可得

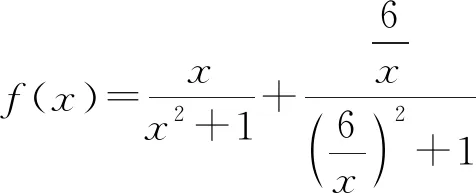
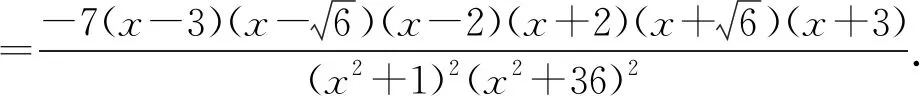
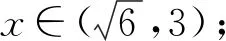
一堂好课的生成,离不开好的数学问题.学生在发现问题、分析问题、解决问题的过程中,有体会、感悟、反思.特别是存在错解的数学问题往往触及学生的知识盲区或能力不足之处,此类问题是学情的“晴雨表”,是教师珍贵的教学资料和备课素材.对于此类问题,教师应当抓住教学契机,引领学生,深刻剖析错误根源,引导学生有逻辑地思考问题,把握事物之间的关联,形成重论据、有条理、合乎逻辑的思维品质和理性精神.