小中见大 高屋建瓴
——2022年全国数学新高考Ⅰ卷第7题的探究与感悟
高玉良, 陈 洁
(1.平湖中学,浙江 平湖 314200;2.台州市双语高级中学,浙江 台州 318000)
在近几年的高考中,频繁出现以指数、对数和幂为载体,考查实数的比较大小问题.此类题目往往与函数、不等式、方程、导数等代数知识相互关联,融入众多数学思想与方法的考查,注重知识本质与思维能力的考查,要求学生有较强的学科素养.2022年全国数学新高考Ⅰ卷第7题正是这样的一道好题.
1 题干虽小,立意高远
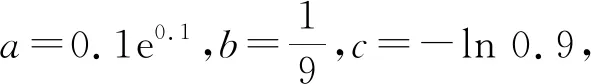
( )
A.a C.c (2022年全国数学新高考Ⅰ卷第7题) 本题答案为C.试题短小精悍,简洁明了,全题只有两个中文文字,以指数、对数和幂为载体,看似考查比较大小问题,实则以小见大,贯穿高中函数知识“主轴”,为我们展示了如何利用函数工具研究“数值估算”问题的一般原理与方法.本题解题入口宽阔,思维方法多样,涉及的知识点有基本初等函数比较大小问题、基本初等函数的导数、复合函数的导数、函数的单调性与导数的关系、不等式的证明与放缩等,突出了数学本质,重视理性思维,有机渗透了数学运算、逻辑推理、数据分析等数学核心素养,体现了解决数学高考试题所需要的思维特点“想得少一点,算得多一点;想得多一点,算得少一点”,以此区分学生的思维层次.因此,这又是一道有“大素养”的数学试题. 要比较a,b,c这3个数的大小,我们可以循序渐进,先从两个数的比较入手,进而得出3个数的大小关系. 思路1由于a=0.1e0.1是以e为底数的指数形式呈现,不便直接与b比较大小,因此可以根据教材所学内容将指数转化为对数,进而比较大小. 方法1利用切线放缩lnx≤x-1(当且仅当x=1时取等号). 即 亦即 从而 于是 故 a 比较a与b的大小等价于比较lna与lnb的大小,即 亦即 lna 故 a 取n=9,得 故 a 方法4构造函数直接作差比大小. 令p(x)=(x-1)2ex-1,则p′(x)=(x2-1)ex<0成立,从而p(x)在(0,0.1]上单调递减,于是 p(x) 即h′(x)<0成立.因此,h(x)在(0,0.1]上单调递减,即 h(x) 故 a 方法5作商比较. m′(x)=-xex<0, 从而m(x)在(0,1)上单调递减,于是 m(x) 故 a 评注作差和作商是比较大小最常见的两种方法.由于当0 方法6作商后利用ex≥ex(当且仅当x=1时取等号)放缩. 当0 故 a 方法7取对数作差. 两式相减,得 (也可以求导证明).故a 评注涉及导数背景下的比较大小问题,利用指数和对数运算的性质,指数作商即为对数作差,同时利用常见切线不等式ex≥ex,ln(1+x)≤x进行放缩.先观察后放缩,可以有效减少计算量,实现小题小做,在考场上节省考生的答题时间,这需要高水平的逻辑推理、数学运算素养. 方法8当0 从而 故 a 本题的难点是比较a=0.1e0.1与c=-ln 0.9这两个数的大小(一个指数、一个对数),初看这两个数风马牛不相及,实则需要扎实的数学功底.试题“思维梯度”设置精巧,发挥了数学高考的选拔功能. 思路1利用不等式将指数与对数放缩到多项式直接进行估算. a-c=0.1e0.1+ln 0.9 故 c a-c=0.1e0.1+ln 0.9 故 c 方法3利用对数均值不等式 令x1=1,x2=0.9,则 即 又a-c=0.1e0.1+ln 0.9 故 c 评注可以发现方法3与方法2的放缩精度是一致的.事实上,这两种方法是等价的,将对数均值不等式 齐次化得 思路2类比比较a与b的大小关系.注意到a=0.1e0.1,c=-ln 0.9=-ln(1-0.1),根据结构特征,构造函数f(x)=xex+ln(1-x)(其中0≤x≤0.1),则a-c=f(0.1),以导数为工具,利用函数性质比较两个数的大小. 方法4二次求导. 当0 (x+2)ex>x+2>2, 又 0.81≤(x-1)2<1, 从而 即f″(x)>0成立,则f′(x)在(0,0.1]上单调递增,从而 f′(x)>f′(0)=0, 于是f(x)在(0,0.1]上单调递增,即 f(x)>f(0)=0, 故 c 方法5局部求导. 令g(x)=(x2-1)ex+1(其中0 g′(x)=(x2+2x-1)ex<0 成立,从而g(x)在(0,0.1]上单调递减,即 g(x) 又因为当0 x-1<0, 所以 f′(x)>0, 从而f(x)在(0,0.1]上单调递增,于是 f(x)>f(0)=0, 故 c 评注在分母确定为负的前提下,判断导函数的正负问题很自然过渡到分子的正负问题,只需对分子部分进行重新求导即可,体现了思维的直观性.这是求导后最自然的方法,也体现了高考真题重视通性通法的特点,也需要高水平的逻辑推理、数学运算、数学建模素养. 方法6导函数局部放缩. 当0 故f(x)在(0,0.1]上单调递增,从而 f(x)>f(0)=0, 故 c 评注函数思维实际上是辩证思维的一种特殊表现形式.既然是因为超越方程的问题无法求f′(x)的零点,那么利用不等式ex≥x+1将指数放缩成多项式进行求解就水到渠成了,这需要高水平的逻辑推理、数学运算素养. 思路3既然可以通过导数判断原函数的单调性进而得出a与c的大小关系,那么直接通过指对数不等式将f(x)转变成多项式问题也就值得尝试了. 故 c f(x)=xex+ln(1-x) 因为(x+1)2(1-x)=x2+2x+1-(x3+2x2+x)=1+x(1-x-x2)>1,所以c 评注将上述各种放缩办法的精确度进行比较,可以得到以下情况: 事实上,当自变量发生变化时,会存在如下的不等式: 这需要更高水平的逻辑推理、数学运算素养. 由高等数学中的泰勒展开式,可以先估算a,c的大小,进而根据估算值比较这3个数的大小. 泰勒公式若函数f(x)在点x0的某邻域内有定义,在x0处存在n阶导数,则在x0附近有 麦克劳林展开式若x0=0,则上述泰勒公式即为 对于函数f(x)=ex,g(x)=ln(1+x),在x0=0处的麦克劳林展开式如下 c=-ln 0.9=-ln(1-0.1) 故 c 评注数学家波利亚曾说过:“没有任何问题是可以解决得十全十美的,总剩下一些工作要做.经过充分的探讨与钻研,我们能够改进这个解答,而且在任何情况下,我们总能提高自己对这个解答的理解水平.”该法借助泰勒展开,抓住问题的本质,作为单项选择压轴题.该题具有高等数学的知识背景,若我们适当了解一些泰勒展开的有关知识,则可以“高观点”地分析问题、解决问题,真正做到“想得多一点,算得少一点”,这需要高水平的数据分析素养. 《中国高考评价体系》指出:高考要求学生能够触类旁通、融会贯通,既包括同一层面、横向的交互融合,也包括不同层面之间、纵向的融会贯通[1].要实现这样的要求,仅靠概括题型和刷题训练是难以实现的,数学教学必须回归学科本质. 从以上对高考问题的解题策略的分析可知,多样性的解法都源于知识之间的关联与联系,而这正是知识的来龙去脉的体现,是数学结构的体现.因此,数学教学必须打破数学概念之间、命题之间的壁垒,帮助学生构建良好的数学认知结构,这是提高数学问题解决能力的关键,也正是单元教学的主要目的. 促进数学概念之间的联系的本质就是促进概念理解.这种联系正好对应3种数学推理形式——归纳、演绎和类比.因此,促进概念理解就是培养数学推理能力. 另外,所有定理、公式和性质的表现形式都是命题,它们的来龙去脉都是数学推理的体现.掌握数学命题的推出过程,获得推出过程中蕴涵着的与这些命题相关的信息,如命题成立的条件、使用功能等,掌握这些信息是对这些命题达到深入理解的标志,是正确、灵活地使用这些命题并解决问题的前提条件. “立意新颖,不为题海战术开方便之门;界定明确,对一线教师的教学有导向功能;有效区分,让不同水平的学生高低立显”是这道高考试题最大的特点,也是课程改革的大趋势,即破除题海战术,加大对学生探究能力、创新能力、思维能力的考查.做题不在多,关键是有思想和方法引领才行,注重通性通法,培养学生养成良好的学习习惯,经常对所学的知识和题型进行总结归纳,寻找规律和突破口,引导学生多方法、多视角思考问题和发现问题.通过对典型题目进行“一题多解、一题多变、多题同解”的训练,帮助学生建构和完善知识网络,培养学生良好的思维品质.但是我们盲目追求题目的解法有多少种是远远不够的,更多地要思考这些解法的共性、本质.题目是千变万化的,但问题的本质是不变的,只有真正理解数学的本质,在平时注重习得基本的数学活动经验,才能洞察数学问题的核心,抓住数学的灵魂,这才是教学所要追求的最高境界[2]. 3.3 切实将核心素养的培养渗透在教学细节中 数学核心素养不是独立于知识、技能、思想、经验值外的“神秘”概念,它们综合体现了对数学知识理解、对数学技能方法的掌握、对数学思想的感悟、对数学活动经验的积累.数学六大核心素养相互关联、互为促进,是一个有机的整体.其中,数学抽象素养主要在数学概念的学习过程中、数学思想方法以及基本活动经验的获得中培养;逻辑推理素养主要在命题证明、问题解决中培养;直观想象与数学运算更是几乎伴随着全部的数学学习;在大量的实际问题解决过程中渗透着数学建模与数据分析的素养.教师在教学中要突出核心素养的培养,注重知识的形成过程,实现学生对知识的主动构建[3]. 本文在分析例1的解答策略中,有意地在评注中剖析了其中所蕴涵的主要数学思想,这些都是教师应该认识到、并有意识地观测平时的教学行为. 2022年数学新高考Ⅰ卷注重考查学生对数学概念、定理等的本质理解,强调基础,基本概念清晰、基本运算过关的考生都能较好解答,展示了数学测试与评价的方向,引导中学数学教学注重提高学生的思维能力、发展应用意识和创新意识,培养数学核心素养,对课程改革的有效实施和深入推进、促进中学数学教学质量的提高有十分积极的作用.数学教学一定要为学生的真正理解而教,为提升学生的思维能力而教,为培养学生的核心数学素养而教.2 策略探寻,灵动多样
2.1 比较a与b的大小
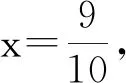
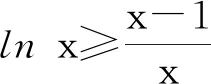
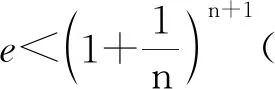
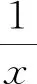
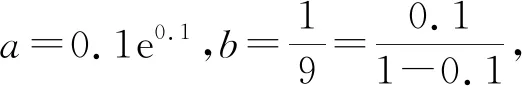
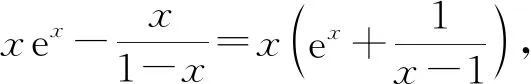
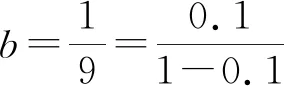
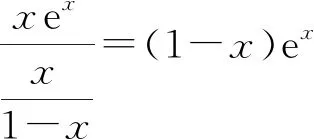
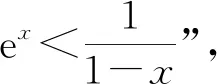
2.2 比较a与c的大小
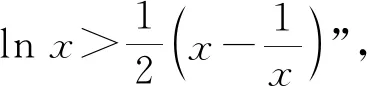
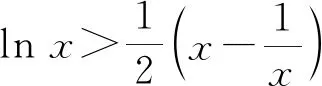
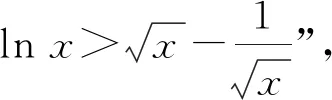
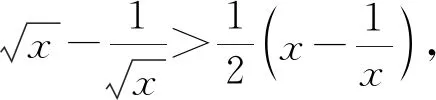
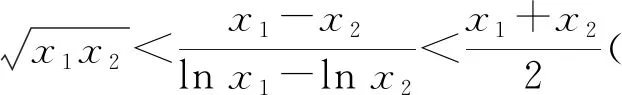
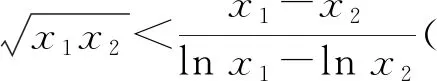
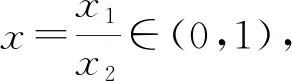
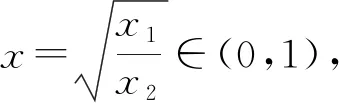
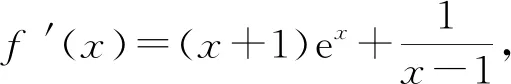
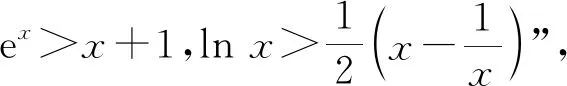
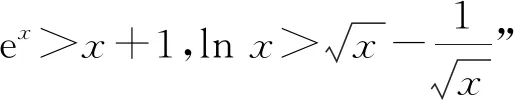
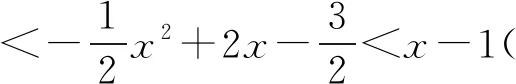
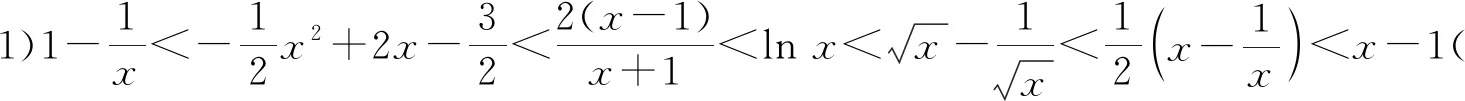
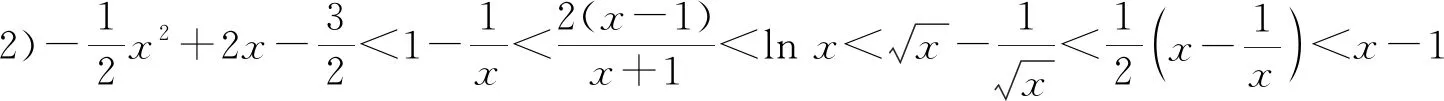
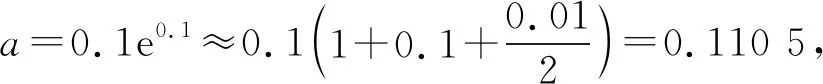
3 反思教学,回归本质
3.1 切实贯彻单元教学的理念,构建数学体系
3.2 培养数学思想方法,习得基本活动经验

