考虑分子链密度的固体火箭发动机粘接界面强度评价方法①
陈尔豪,雷 鸣,文立华,校金友*,侯 晓
(1.西北工业大学 航天学院,西安 710072;2.中国航天科技集团有限公司,北京 100089)
0 引言
固体火箭发动机结构中存在多种复合界面,能够显著降低结构装配难度且具有抗疲劳、密封性好等优势[1-4],其中燃烧室粘接界面是发动机的关键组成,其连接可靠性是固体火箭成功发射的关键,而粘接界面的连接性能受环境载荷及加载历史影响较大,质量控制与结构可靠性评估较为困难[5-6]。准确表征和预测燃烧室粘接界面在贮存以及服役过程中的性能演化,是确保发动机正常点火工作的关键[7-8]。
为揭示燃烧室粘接界面的力学性能演化规律,国内外众多学者进行了诸多努力,SIH[9-10]基于内部热量产生和能量耗散效应的等能量密度理论,研究了发动机的界面脱粘,发现界面的裂纹扩展主要取决于瞬态载荷。HO[11]通过测量评估了临界温度以及热力耦合循环次数对粘接界面性能的影响,基于内部能量耗散理论表征出粘接界面的破坏模式。SRINIVAS等[12]基于断裂力学相关理论,提出了一种粘弹材料界面中裂纹扩展的判据。国内有张兴高等[13]研究了NEPE推进剂贮存老化过程中各项性能的变化,发现老化失效主要表现为强度失效。邱欣等[14]设计出一种粘接试件并进行了在位拉伸试验,研究了高氯酸铵颗粒对界面脱粘的影响。郭翔等[18]对粘接界面模型进行了非线性粘弹性分析,确定了衬层性能对粘接界面的影响。姜爱民等[7,19-20]使用数字图像相关技术(digital image correlation, DIC)对粘接界面试件拉伸变形破坏过程进行了观察,并研究了各层材料性能参数和结构参数对粘接系统力学性能的影响。周清春等[21-22,26]通过试验改进了指数型内聚力模型用于预测粘接界面的断裂性能。刘磊等[27]通过单向拉伸试验测试了粘接试件的最大应力强度,得到了试件粘接强度随振动时间的演化规律。然而,以上研究大都基于经典断裂理论开展[30-34],未考虑粘接界面在贮存、服役中的分子链交联密度演化问题;而高分子链的交联情况与粘接界面性能直接相关,是准确分析粘接界面力学响应的基础参量[15-17]。此外,经典断裂理论主要适用于金属的断裂过程[23-24],在裂纹尖端之前,材料只发生了塑性变形;而对于推进剂等材料的聚合物基复合界面,在裂纹尖端之前,材料已经发生了部分断裂,其裂前交联密度显著降低[28-29]。
为了建立刻画真实物理过程的粘接界面强度演化模型,本文发展了一种基于高分子交联链密度(简称分子链密度)的粘接界面强度评价方法,为准确追踪、评估推进剂在复杂工况下的燃烧室界面可靠性奠定了基础。
1 研究思路与试验方案
1.1 总体研究思路
本文的核心为研究在不同挂载历程下燃烧室粘接接面极限应力、界面能量随挂载载荷、挂载时间和拉伸速率的演变关系。因此,需要首先获取HTPB推进剂的粘接界面力学性能随挂载历史的演化关系。总体研究思路如下:
(1)首先获得原始试验件(未经历挂载)的载荷-位移曲线:控制温度为室温(25 ℃)左右,拉伸速率为2、20 mm/min,采用单轴拉伸试验获得试验件的I型断裂过程参数。
(2)将试验件进行50、100、150、200 d挂载以模拟发动机中复合界面在运输、贮存中的加载历史,而后进行拉伸试验,获得经历挂载历史后的试验件的载荷位移曲线。
(3)计算极限应力以及界面能量,考察挂载条件(载荷与挂载时间)以及拉断时加载速率对极限应力以及界面能量的影响规律。
1.2 试验装置与试验方案
界面试验件测试过程依照 QJ 2038.1A“固体火箭发动机燃烧室界面粘接强度测试方法”[35]。试验件尺寸与人工预制脱粘区位置如图1所示。

图1 界面试件尺寸
试验参数设置:
(1)考虑固体发动机在运输、贮存、服役过程的实际受载情况,选择试验拉伸速率为2、20 mm/min。
(2)根据固体发动机在不同服役阶段的工况,取挂载载荷为0(未经历挂载)、0.075、0.150、0.225、0.300 MPa。
(3)为模拟固体发动机贮存不同的时间后的界面力学响应,取挂载时间为0(未经历挂载)、50、100、150、200 d。
在拉伸试验过程中,采用数字图像相关技术(DIC)测量拉伸试样全场应变,利用Sony A7R3相机配备焦距为135 mm的定焦镜头测量散斑的位移,记录图像和数据,在测试完成后,用数字图像追踪软件(研索仪器科技有限公司,上海)进行后位移场后处理,获取矩形试样的开裂过程的全场应变。图2所示为未经历挂载试件在25 ℃,拉伸速率20 mm/min条件下的试验结果,界面试件的上端存在两处对称的预制裂纹,在拉伸过程中宏观裂纹尚未扩展时,应力集中位置出现在预制裂纹尖端处,且应力与位移云图呈现出较好的对称性(图2(b));虽然在拉伸初始阶段呈现对称性,在实际试验过程中裂纹总是从某一段扩展延伸至另一端,当试件某一侧裂纹开始扩展后,该侧强度迅速降低,裂纹向另一端快速扩展(图2(c)),另一端预制裂纹尖端处应力集中现象缓解,此时位移云图不再呈现对称特征。

(a)Testing sample in the interface experiment
2 试验结果
2.1 未挂载试验件的试验结果
首先分析未经历挂载的试验件界面性能。如图3所示,未经历挂载的界面试样件在20 mm/min的极限载荷约为2.85、3.00、3.15 kN,故认为原始试样在20 mm/min的极限载荷约为3.00 kN;在2 mm/min的极限载荷约为2.60、2.40、2.58 kN,原始试样在2 mm/min的极限载荷约为2.53 kN。从原始试验件的结果可知,拉伸速率对试件界面力学性能有着显著影响,在低应变率作用下的试件表现出的极限载荷较低。在低应变率条件下,粘接界面的分子链部分有较长时间发生松弛及断裂;当加载应变率升高,界面的分子链尚未松弛,表现为直接破坏[25]。因此,在试验中表现为极限载荷随应变率的升高而增加。

图3 未经历挂载试验件的载荷-位移曲线
2.2 挂载后试验件的试验结果
进一步讨论挂载历史对界面力学性能的影响,如图4所示,依次为挂载50、100、150、200 d的试验结果。可以看出,挂载的载荷以及拉伸速率对推进剂界面的力学性能有显著的影响,随着挂载载荷的增大以及拉伸速率的减小,界面试件的极限载荷变小、断裂延伸变差。拉伸速率对于未经历挂载和经历挂载后的试件影响模式一致;在挂载时,粘接界面的分子链部分由于挂载载荷的作用而被破坏,且分子链的破坏程度与挂载载荷呈正相关。因此,在试验中表现为挂载载荷较大的试件其界面力学性能较差。

(a)The loaded testing samples for 50 days (b)The loaded testing samples for 100 days
3 结果讨论
3.1 试验结果数据分析
为更精确地分析界面力学性能的演变规律,在试验所得的载荷-位移曲线基础上,可进一步计算出界面能量,即曲线围成面积即为试件的界面能:

(1)
式中E为界面能量;F为试件所受载荷;ds为受载F时移动的微小距离;Sf为总拉伸位移。

在后续分析中,将主要依据试验获取的挂载后矩形试样件的“界面极限应力”以及“界面能量”两项指标进行讨论。试验结果如图5~图8所示。

(a)Ultimate stress vs loading stress curves at 2 mm/min (b)Ultimate stress vs loading stress curves at 20 mm/min
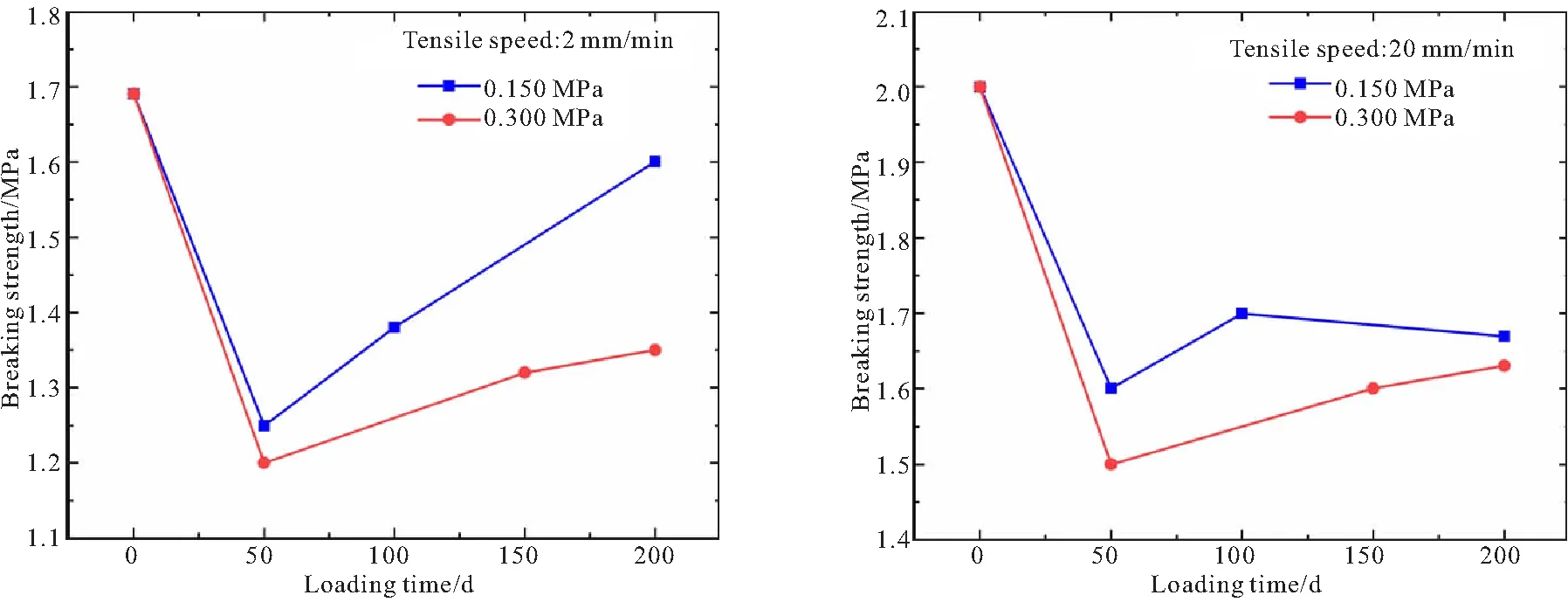
(a)Ultimate stress vs loading time curves at 2 mm/min (b)Ultimate stress vs loading time curves at 20 mm/min

(a)Interface energy vs loading stress curves at 2 mm/min (b)Interface energy vs loading stress curves at 20 mm/min

(a)Interface energy vs loading time curves at 2 mm/min (b)Interface energy vs loading time curves at 20 mm/min
图5(a)给出了拉伸速率为2 mm/min条件下测得的界面极限载荷应力随挂载应力载荷的演化情况。可见,对于挂载50、100、200 d试样,界面极限应力均随挂载载荷增加而逐步减小,即较大的挂载应力会导致粘接面承载能力减弱。但对于挂载载荷0.150 MPa、挂载时间200 d的试验数据发生了反常,可能的原因是“试验误差”,或是由于“挂载过程中在天左右界面发生了二次交联,导致界面强度有所升高”。图5(b)给出了在拉伸速率为20 mm/min条件下测得的界面极限载荷应力随挂载应力载荷的演化情况,同2 mm/min拉速结果类似,对于挂载50、200 d的试样,界面极限应力随挂载载荷增加而逐步减小,即较大的挂载应力会导致粘接面力学性能显著下降。
图6(a)给出了拉伸速率为2 mm/min条件下测得的界面极限载荷应力随挂载时间的演化情况。类似的,图6(b)给出了拉伸速率为20 mm/min条件下测得的界面极限载荷应力随挂载时间的演化情况。可以看出,不论挂载应力大小,粘接面极限应力在挂载过程中均先减小、后增大。
图7(a)给出了拉伸速率为2 mm/min条件下测得的界面能量随挂载载荷的演化情况;类似的,图7(b)给出了拉伸速率为20 mm/min条件下测得的界面能量随挂载载荷的演化情况。可以看出,随挂载载荷增加,界面能显著减小。
图8(a)给出了拉伸速率为2 mm/min条件下测得的界面能量随挂载时间的演化情况。同样,图8(b)给出了拉伸速率为20 mm/min条件下测得的界面能量随挂载载荷的演化情况。可以看出,界面能不显著依赖于挂载时间。如图8(a)所示,在0.150、0.300 MPa挂载条件下,界面能量随挂载时间仅略有起伏,即界面能曲线在以时间为自变量时,界面能量沿时间变化时曲线起伏较小,可近似认为在此试验参数范围内挂载时间对界面能量影响很小。因此,在以上试验所包含的挂载载荷与挂载时间范围内,界面能与挂载载荷相关,受挂载时间的影响较小,可认为与挂载时间无关。
综上所述,与极限应力相比而言,界面能指标更加稳定。界面能是界面试样断裂过程中的能量综合判断,不依赖于预制裂纹前端界面质量;而极限应力是由裂纹初始扩展时刻的载荷计算得到,显著依赖于预制裂纹前端界面质量,试验所得数据有一定波动,规律性较差。因此,后续预测模型依据测量所得到的界面能演化进行讨论。
3.2 分子链密度模型演化预测
基于以上试验结果,依据高分子物理[1],发展得出界面能随挂载历史的演化方程。由上述试验结果可知,在小应力挂载条件下,界面能与挂载时间无关,只与挂载应力相关,故在演化方程的推导中,暂不考虑挂载时间的影响,仅考虑挂载应力这一因素。挂载时,挂载应力对界面的输出能量为
(2)
其中,此处粘接试验的界面能随挂载应力呈指数关系[1],且挂载应力为σpre,而挂载应变为εpre。挂载应力所作功的部分转换为推进剂弹性应变能等,另一部分则用于拉断界面的分子链,转换为界面的断裂能量。
界面的初始交联密度为Nint,在小挂载应力作用下,分子链逐步发生断裂,随着挂载应力的增加,分子链会断裂至完全,即Nint→0,将尚未发生断裂的分子链密度记为N。实际上决定界面强度的是挂载后当前条件下的分子链密度N。则可假设界面能G正比于分子链的交联密度[1],即有GN,粘接界面的分子链示意图如图9所示,上下两端面为两种不同的材料,在推进剂浇注过程中两材料的分子相互扩散渗透,并发生大规模交联形成高分子网络,最终形成界面;在界面处交联密度逐步过渡,宏观界面模量呈梯度演化。
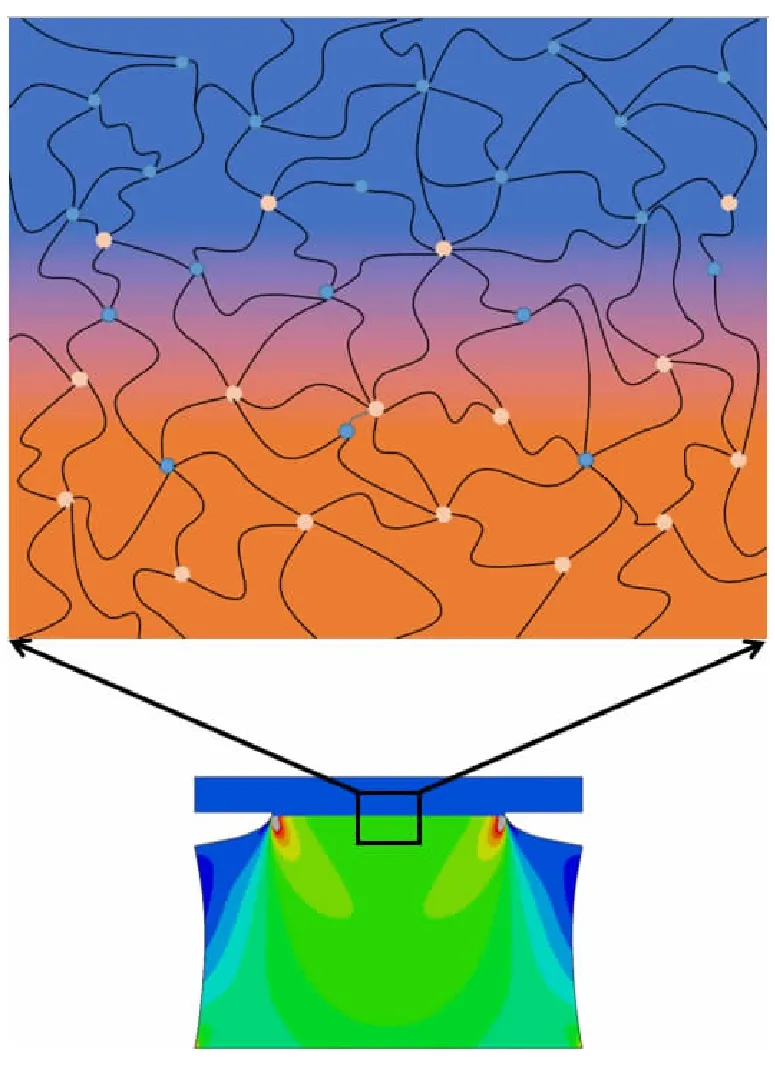
图9 粘接界面分子链示意图
在挂载应力输出能量Epre作用下,Nint逐步发生断裂,分子链的断裂过程正比于能量壁垒kT(k为玻尔兹曼常数;T为体系的绝对温度)。则有
简化后可得
(3)

在试验中,测量的界面能不仅与测试条件(温度、应变率)相关,而且与相对交联密度n相关[1],因此有
(4)

(5)
即c=0.06478,如图10所示。

图10 剩余相对交联密度随挂载载荷的演化预测
由图10可知,理论模型与试验数据点匹配良好,能描述剩余相对交联密度在小挂载条件下的演化趋势。实际上,上述线性理论仍未考虑到界面在较大挂载应力下的非线性加速行为。当挂载应力较大时,界面分子链将发生大规模断裂,而剩余分子链数目显著减小。此时,由于宏观挂载应力不变,单根分子链上的挂载应力将快速增加,导致相对交联密度迅速减小、宏观界面快速断裂。因此,在高应力挂载区域,图10所示的剩余相对交联密度将显著偏大。
考虑到未挂载情况下,所测量得到的初始界面能量分别为G0(2 mm/min,25 ℃)=9.50 J,G0(20 mm/min,25 ℃)=13.85 J。因此,由式(4)可以得到随挂载载荷、拉伸速率相关的界面能量预测,如图11所示。可以看出,在剔除试验异常数据点后,该模型理论曲线与试验所得数据点吻合良好,说明该模型可以较好地预测试件界面能量随挂载载荷的变化关系,能够为后续以界面能量作为界面强度准则以及固体发动机结构完整性的分析研究提供一定的参考。
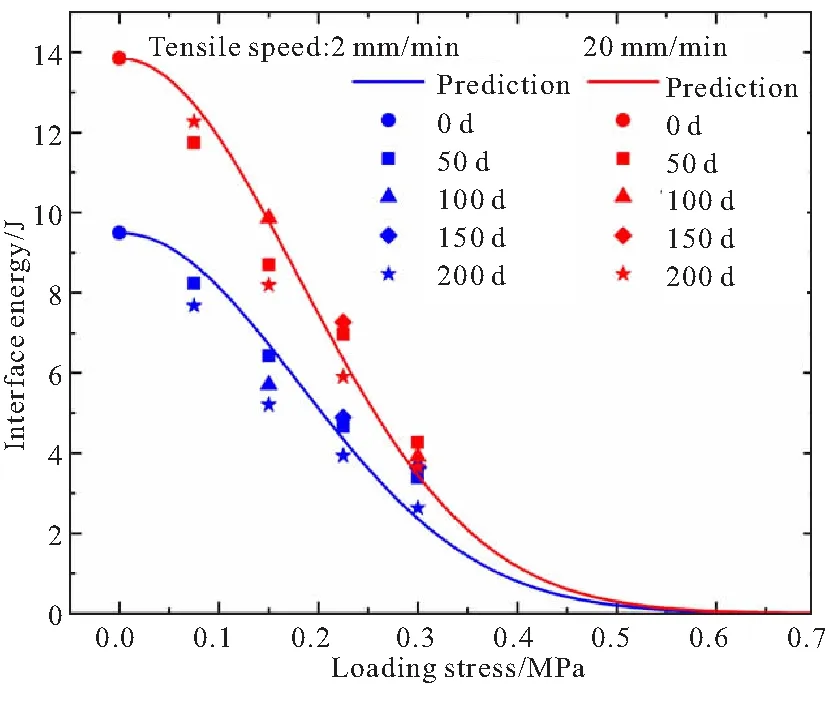
图11 界面能随挂载载荷的演化预测
4 结论
(1)与界面极限应力载荷相比而言,界面能是更加合理地判断界面性能的指标。
(2)在小应力挂载条件下,粘接面力学性能(界面能量)显著依赖于挂载应力,几乎不依赖于挂载时间。
(3)基于分子链交联密度演化,在较小应力范围与实验所进行的时间范围(≤200 d)条件下,能够很好预测界面能随挂载应力的演化关系。

