Prony级数的不同阶数对HTPB推进剂力学响应仿真影响①

贾乐凡，史宏斌，沙宝林，许 杨

(西安航天动力技术研究所，西安 710025)

0 引言

HTPB推进剂被广泛用于各型航天器、空间飞行器固体发动机上[1]。其力学响应行为与温度、加载方式、加载历程等诸多因素相关[2]。国内外针对HTPB推进剂本构方程进行了大量研究。HTPB推进剂基于本身的高填充比和固化弹性体结构表现为典型的非线性粘弹性复合材料，此类材料在应变较大时呈现明显的应力-应变非线性特征[3]。针对HTPB推进剂本构方程的建立方法主要包括单独使用弹性/粘弹性/超弹性模型[4-5]、弹性模型耦合蠕变模型[6-7]、粘弹性模型耦合超弹性模型[8-9]。此外，还有HTPB推进剂本构方程耦合塑性模型[10]、老化模型[11]、损伤模型[12]等其他模型的研究。目前，大部分本构方程建立的核心是表征HTPB材料的粘弹性响应特征。而Prony级数方程作为一种较为简单的线性粘弹性本构方程得到了广泛应用。在基于Prony级数的模型建立过程中，首先需要确定Prony级数阶数，随着Prony级数阶数增高，其占用的计算资源呈指数增加。因此，在实际应用过程中Prony级数阶数并非越高越好，而要结合数值模拟目的与计算资源现状选取合适的Prony级数的阶数。一般工程计算中这一取值由经验给出，未见针对不同阶数的Prony级数对数值模拟结果影响的专门研究。

本文根据试验获得HTPB松弛模量主曲线，建立其5～10阶Prony级数模型并进行数值模拟，探究不同阶数的Prony级数对HTPB推进剂数值模拟研究产生的影响，并尝试给出不同情况下适用的级数阶数。所得结论可应用于HTPB推进剂相关数值模拟研究，为其相关工程应用提供借鉴。

1 粘弹性本构方程

对于简单的粘弹性材料，其应力-应变曲线与时间具有相关性。在此基础上，如果其本构关系符合叠加性原理：

σ(ε1+ε2)=σ(ε1)+σ(ε2)

(1)

以及齐次性原理：

σ(βε)=βσ(ε1)，(β=const)

(2)

则可将其视为线性粘弹性材料。

对于简单的线性粘弹性材料，其应力与应变历史有关：

(3)

式中E(t)为松弛模量，通过定应变试验测得。

对于与温度相关的线性粘弹性材料，需要在积分中将温度依赖项与时间依赖项分离：

(4)

式中ξ为缩减时间。

(5)

式中αT为时间-温度平移因子，是关于温度的函数，其值通过定应变试验拟合而出。

目前，常用的线性粘弹性模型主要包括Maxwell模型、Voigt模型等[13]。其中，Prony级数模型，作为一种广义Maxwell模型在工程上应用最广。该模型可视为一个胡克弹簧与若干个Maxwell模型并联，其阶数可等效视为并联的Maxwell模型个数。常用的Maxwell模型可视作1阶Prony级数模型。无量纲形式的Prony级数为

(6)

式中gR(t)为无量纲松弛模量；N为方程阶数；τi为材料的松弛时间。

对基于Prony级数的粘弹性本构方程，其数值计算结果与其阶数N有关，在实际应用过程中，需结合数值模拟目的与计算资源现状选取合适的级数阶数。本文针对HTPB推进剂粘弹性本构方程，研究不同阶数对其数值模拟研究产生的影响。

2 数值模拟

2.1 物理模型

通过单向拉伸试验得到的HTPB推进剂应力-应变曲线，获得其松弛模量主曲线，如图1所示。

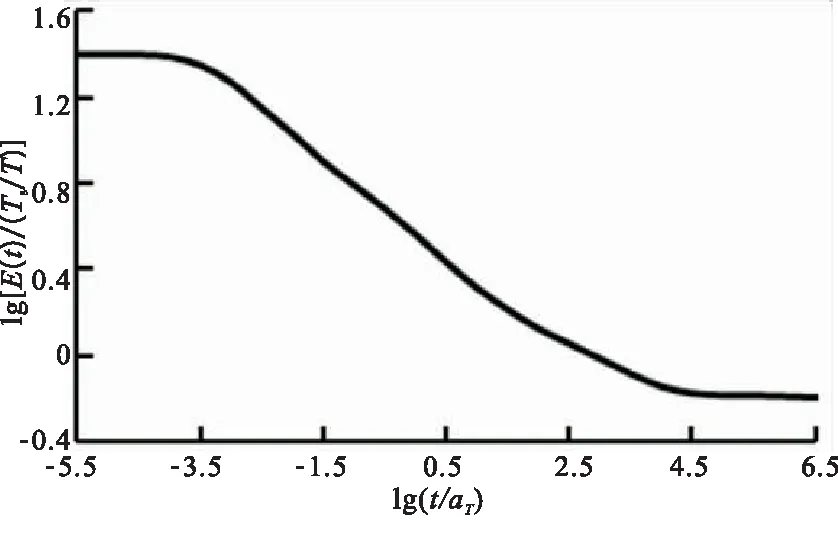
图1 THPB应力松弛模量主曲线(Ts=293.15K)

根据松弛模量主曲线及时间-温度平移因子拟合得到无量纲Prony级数各阶的松弛模量系数，如表1所示。以表1数据作为材料模型，根据单轴拉伸试验标准建立数值仿真模型。图2为试件几何尺寸，图3为其模型示意图。

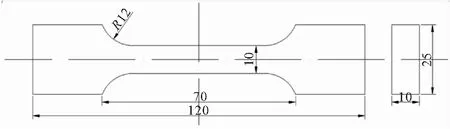
图2 试件模型(单位：mm)

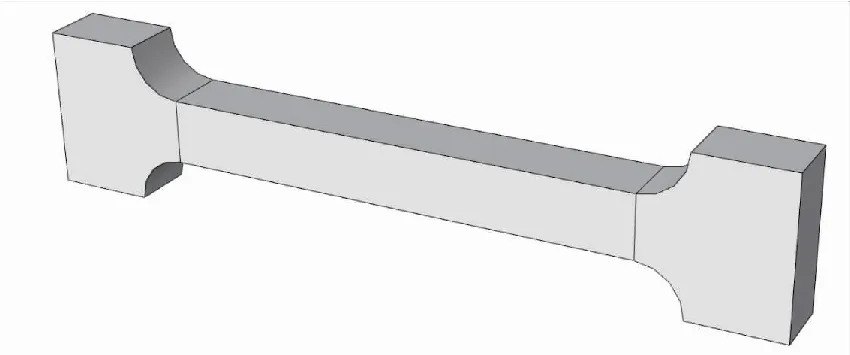
图3 哑铃形试件模型示意图

表1 各阶Prony级数参数

分别将5～10阶Prony级数方程作为试件材料参数代入，对模型一端施加固定边界条件，另一端施加60 mm位移边界条件。分别设置分析步时间间隔为3600、360、36、12、7.2 s，以模拟试件在试验时所经历各拉伸速率下的力学响应得到其应力-应变曲线，并与试验结果进行比对。

2.2 仿真结果

图4为Prony级数取5～10阶时模型在1、10、100、300、500 mm/min拉伸速率下的应力-应变曲线。

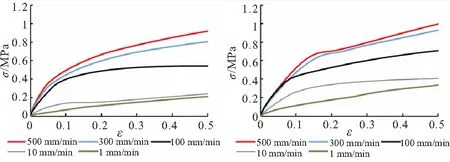
(a)N=5 (b)N=6

由图4可以看出，各阶级数模型仿真结果均随拉伸速率增高而增大。在5阶时，模型在500 mm/min拉伸速率下应力最大值约0.79 MPa，在1 mm/min拉伸速率下应力最大值仅有0.15 MPa；当拉伸速率较低时，其曲线斜率变化不大，而当拉伸速率较高时，其整体拉伸曲线呈现典型的双线性特征。这是因为Prony级数模型在较短时间历程的拉伸过程中主要表现弹性体特征，而在较长时间历程内表现蠕变特性。

此外，综合分析各阶级数仿真结果可以看出，拉伸速率较高时，各阶Prony级数仿真结果较为接近；在拉伸速率较低时，Prony级数阶数越高，低拉伸速率下仿真结果越大。这是因为在拉伸速率较低(1 mm/min或10 mm/min)时，模型的力学响应受蠕变特性影响较大，高阶Prony级数能够更好地模拟材料的蠕变行为。因此，其结果随阶数升高而增大。

3 试验结果与讨论

3.1 试验仪器与方案

试验仪器为深圳三思纵横UTM520HB电子万能试验机，试验对象为依照QJ 924—1985《复合固体推进剂单向拉伸试验方法》[14]制成的某配方HTPB推进剂试件，其配方如表2所示。

表2 HTPB推进剂配方

在20 ℃条件下进行拉伸速率为1、10、100、300、500 mm/min的HTPB推进剂单轴拉伸试验，得到试件的应力-应变曲线。

3.2 试验结果

试验在每个拉伸速率下均进行3次。其中，除一组试件在300 mm/min拉伸速率下提前断裂(分析排除试验设计原因)外，其余各组在相同拉伸速率下的结果均十分接近。在两组完整数据中，选取一组结果作为后续数值模拟研究参考。试验获得的HTPB推进剂不同拉伸速率下应力-应变曲线如图5所示。可以看出，HTPB推进剂在不同拉伸速率下表现出明显的粘弹性特征，其应力应变与加载历程有关；在同样拉伸应变下，应力随应变率的增大而增大。

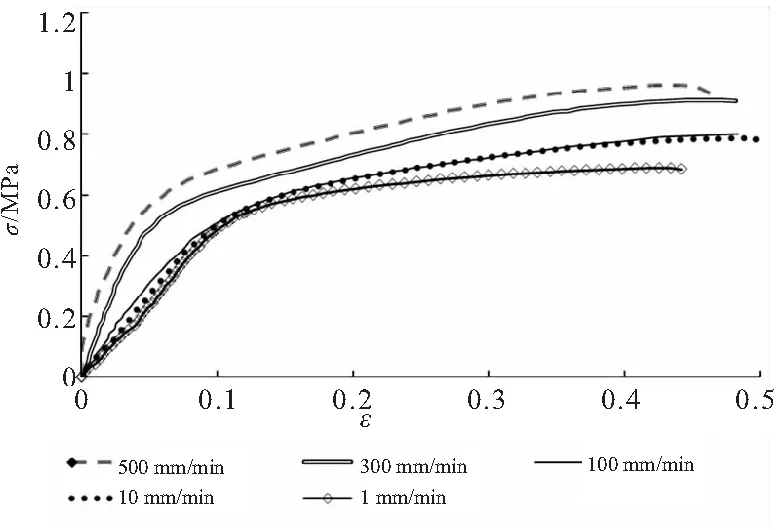
图5 不同拉伸速率下推进剂应力-应变曲线

结合试验结果可以看出，粘弹性材料拉伸过程中，应力-应变曲线与拉伸速率有关，需要分析不同拉伸速率对各阶Prony级数方程数值模拟结果的影响。

图6为不同拉伸速率下的各阶Prony级数模型仿真结果与试验结果对比。比较不同拉伸速率下的试验与数值模拟结果看出，不同拉伸速率下Prony级数模型仿真结果均随阶数的增高而向试验结果逼近，这是因为高阶的Prony级数模型能够更好地反映材料模型的实际力学特性。

(a)1 mm/min (b)10 mm/min

由图6可见，当拉伸速率较高时，各阶Prony级数模型结果差别不大；而当拉伸速率较低时，仿真结果误差随着阶数降低而快速增大。这是因为Prony级数模型瞬时响应呈现弹性体特征，而时间效应呈现粘性体特征。当拉伸速率较高时，材料主要表现弹性效应，因此不同阶模型结果差异较小；而当拉伸速率较低时，高阶级数模型能够更好地表征材料的粘性响应，因此高阶模型相比低阶模型误差明显减小。此外，可以看到试验中试件相较仿真总是更早进入损伤阶段。这是因为相比于实际情况，仿真模型无法反映试件在成型过程中的微观缺陷或损伤，因此其结果更加理想化。

3.3 不同拉伸速率下各阶Prony级数模型仿真误差比较

在单轴拉伸试验中，其应力通过测力装置读数除以截面面积计算得到，为试验原始数据。因此，以试验所测得应力值作为基准分析模型仿真误差，取每一有效试验应力数据点与各个仿真结果应力数据点距离最小值为其误差，由此得出不同拉伸速率下的各阶Prony级数模型仿真误差。

图7反映了不同拉伸速率下各阶模型仿真误差之间的关系。可以看出，不同拉伸速率下Prony级数模型仿真误差总体上均随阶数的增高而减小。当拉伸速率较低时，阶数对仿真误差的影响尤为明显，阶数过低时，其平均相对误差甚至大于50%。随着拉伸速率的增大，仿真误差对阶数取值的敏感性逐渐降低。当拉伸速率在100 mm/min以上时，其各阶平均相对误差均能保持在15%以内。因此，当需要计算的物理情形下应变率较高(拉伸速率较高)时，可以适当降低模型的阶数来提高计算效率，而当应变率较低(拉伸速率较低)时，需要适当提高模型阶数来保证计算结果精度。

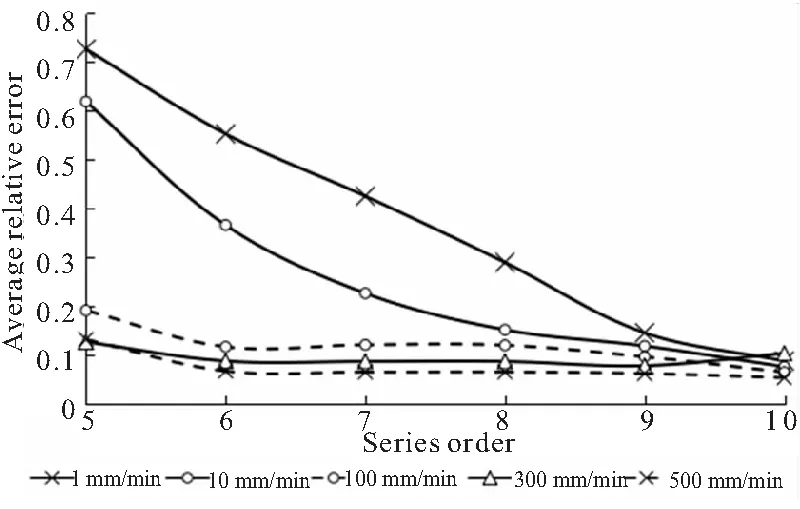
图7 不同拉伸速率下各阶级数仿真误差比较

进一步观察数据可以看出，拉伸速率较低时，低阶方程误差极大，但其误差随着阶数增高迅速减小；当阶数达到10阶时，模型仿真误差受拉伸速率变化影响较小。各阶方程误差大体上随拉伸速率增大而减小，同一拉伸速率下的方程误差大致上随阶数增高而减小。当拉伸速率较低时，小于9阶的方程误差较大，不能符合实际情况；当拉伸速率较大时，6阶以上的模型误差均相对较小，但考虑到实际仿真时的情况，即使拉伸速率较大时，基于Prony级数的粘弹性模型阶数也应取不小于7阶。

4 结论

(1)利用Prony级数计算HTPB推进剂粘弹性力学响应时，其阶数最好不小于7阶；在小于7阶时，模型数值仿真计算结果误差大多偏离试验数据10%以上，与材料实际力学行为有较大差异；当计算贮存、运输等缓慢加载工况时，其阶数最好不小于9阶。

(2)当拉伸速率较高时，各阶级数仿真结果与试验相差较小，但随着拉伸速率下降，低阶Prony级数的仿真误差迅速增大。

(3)当拉伸速率较高时，可采用较低阶数的Prony级数模型以提高计算效率；而当拉伸速率较低时，需要采用高阶Prony级数方程以更好地模拟材料蠕变特性。

本文结论适用范围为未进入损伤阶段的HTPB推进剂。其结论可用于HTPB推进剂的简单工程计算及强度校核，并为其安全裕度设计及失效判定提供理论依据。