带时滞与Monod-Haldane功能性函数的分数阶阶段结构食饵-捕食模型的Hopf分岔

马 溧，李周红

（1.楚雄师范学院 附属中学，云南 楚雄 675000；2.云南财经大学 统计与数学学院，云南 昆明 650048；3.玉溪师范学院 数学与信息学院，云南 玉溪 653100）

0 引言

种群动力系统近年来受到许多研究者的关注，大多数将其建立微分方程来研究其稳定性[1].食饵-捕食者相互作用的动力学关系是数学生物学最重要的研究模型之一.在20 世纪，Volterra 和Lotka 建立了生态系统模型，在恒定和统一的环境下，一个捕食者种群和一个猎物种群.该模型被称为标准Lotka-Volterra食饵-捕食模型，可以用微分方程或差分方程来描述，它引起了应用数学和理论生态学的广泛关注.另一方面，在食饵-捕食系统的种群动态研究中，已经有许多学者做了大量的研究工作[2～6].然而，捕食者和食饵的增长速度是不受限制的，这与现实世界的情况相矛盾.文献[7]讨论了分数阶神经网络的分岔和稳定性问题.生态系统中主要的功能性反应函数有Holling-Ⅰ-Ⅳ型、Beddingtondeangelis 型、hassel-verley 型，其中还有一种Monod-Haldane 功能性函数.事实上，建立更具实际的食饵-捕食模型，特别是不同物种对捕食现象所带有的功能性反应函数，是有研究意义的.文献[8]研究了一类非自治阶段结构捕食系统的持续生存模型，模型将食饵种群分为幼年和成年阶段，且幼年被捕食的可能性很大，相反成年具备较强的抗捕食能力，模型表述如式（1）.

式（1）中，x1(t)表示食饵在t时刻的种群密度，x2(t)和x3(t)表示幼年期和成年期t时刻捕食者的种群密度.p是被捕食物种在没有捕食物种的情况下正常生长的生物潜力.K为环境承载力.δ是成熟捕食者对猎物的最大摄取量.ß为抑制系数，φ为半饱和常数.c定义了转换系数（幼年期到成年期的转换），κ表示幼年捕食者和成年捕食者进化的转换率.μi(t=1，2)为幼年捕食者和成年捕食者种群的自然死亡率，τ表示时滞，即从幼年转变到成年所需要的时间.

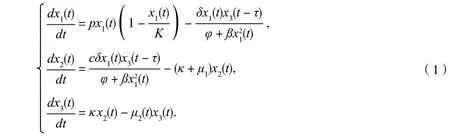
众所周知，有两种类型的微分系统：整数阶系统和分数阶系统.传统上，整数阶系统比分数阶系统更受青睐.因为整数阶系统在数学上易于处理.事实上，分数微积分是一个经典的数学概念，有300 多年的发展历史，可以将分数阶推广到任意的整数阶，在物理学中、生物学和工程学等中扮演着重要角色[9].文献[10～14]研究了分数阶神经网络和种群系统的动力学研究.石敏等研究了一个分数阶小世界网络模型的稳定性与Hopf 分岔延迟控制等问题[15]，徐昌进等人研究了分数阶混沌金融模型的时滞反馈控制策略问题[16].

它的重要性体现在3 个要点：第一，分数阶微积分中，导数和积分的阶数都是实数；第二，分数阶导数具有记忆和遗传特性；第三，分数阶导数建立的模型比整数阶模型更精确.基于这些优点，分数阶微积分近年来被提出用于生态系统、神经网络的建模、设计和控制.例如，如文献[17]，作者讨论了具有不同阶数的两个捕食者和一个食饵的时滞生态系统模型.进一步引入线性时滞反馈控制策略，对时滞分数阶系统产生的分岔进有效地控制.

受上述文献的启发，本文将利用分数阶微积分的理论，基于时滞和分数阶作为参数，讨论如下带有时滞和Monod-Haldane 功能性反应函数的食饵-捕食模型：

其中，φ∈(0,1]是分数阶，其他参数背景意义与系统（1）一致.事实上，当φ=1 时，系统（2）化简为系统（1）.

本文的工作主要是利用分数阶理论，基于时滞分岔参数，讨论系统（2）的Hopf 分岔问题，进一步分析了带时滞控制系统的动力学行为.

1 分数阶系统理论

为给出本文的主要结果，先给出一些必要定义和引理.

分数导数有几种定义，其中Riemann-Liouville 的定义和Caputo 的定义是常用的两种定义.因为Caputo 导数的定义使得它更适用于现实世界的问题.文中采用了Caputo 导数的定义.

定义1[9]函数x(t)的阶数为q∈R+的分数阶积分定义为

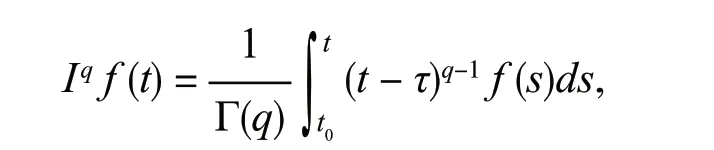
其中，t≥t0，q＞0，Г(·)是Gamma 函数，

定义2[9]函数x(t)∈Cn([t0,∞),R)的阶数为q的导数定义为

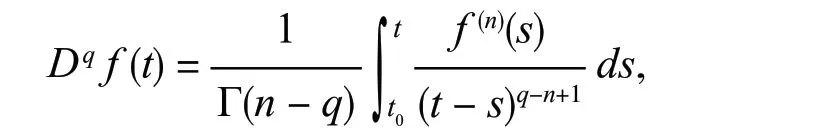
其中，t≥t0，且n是一个正整数使得n-1≤q＜n.

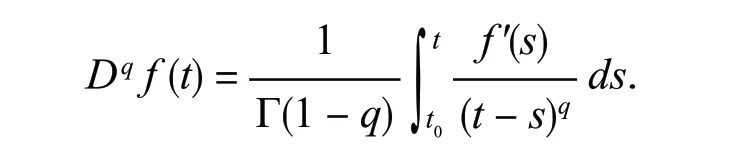
进一步，当0 ＜q＜ 1 时，

引理1[9]由于考虑到分数阶线性系统Dqx=Ax，其中x∈Rm，A∈Rm×m，φ∈(0,1]，则有：

（1）系统Dqx=Ax是渐近稳定的，如果矩阵A的任意特征值λ有|arg(λ)|＞成立.

（2）系统Dqx=Ax是稳定的，如果矩阵A的任意特征值λ有|arg(λ)|成立.

2 主要结果

2.1 无控系统Hopf分岔

由分数阶微分方程稳定性理论可知，系统（2）有一个唯一的正平衡点经计算E*为

在本文中，我们的基本假设如下：

我们将以时滞为分岔参数，研究系统（2）的稳定性和分岔.

当条件（H1～H2）成立，原点是系统（2）的一个平衡点.系统（2）在原点处的线性方程为

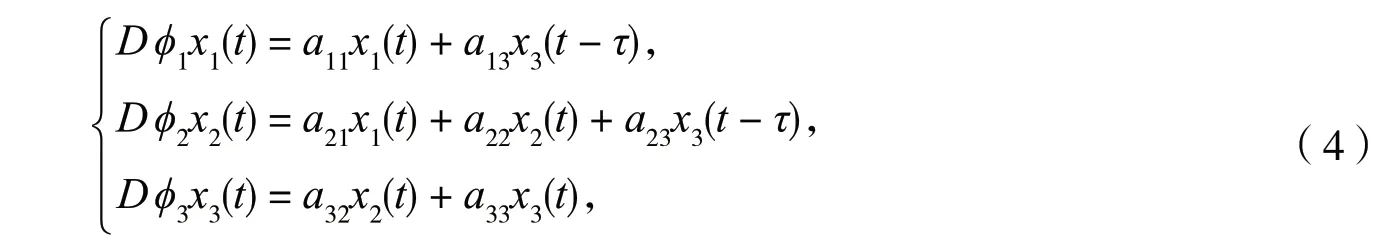
则系统（4）的特征方程为

通过（5）我们可以得到

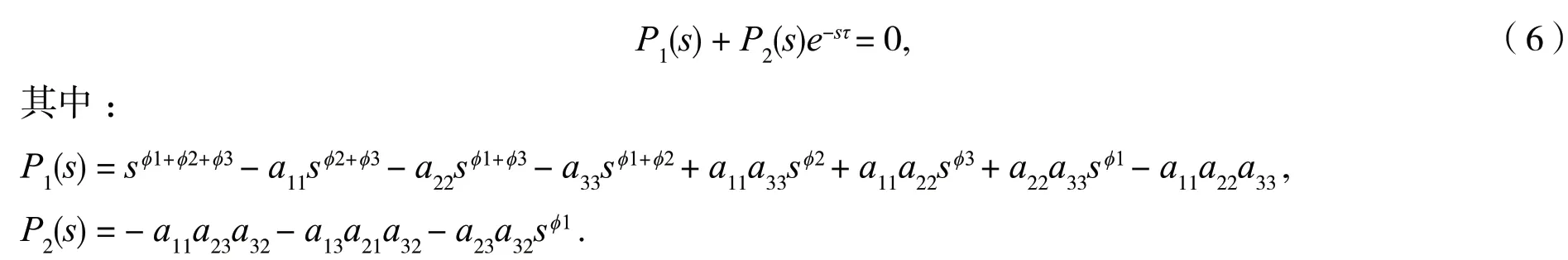
令P1(s)=A1+iB1,P2(s)=A2+iB2，由式（6）可知，

设s=iω=是方程（7）的一个根.将s代入式（7），分离它的实部和虚部，可以得到

应用式（8）直接计算得到

因为

由于cosωτ=F(ω)，我们得到

定义分岔点

式（12）中，τ(κ)由式（11）给出.

进一步，我们将给出以下假设：

（H3）：方程（10）至少有一个正实根.

其中，θ1=a11+a22+a33，θ2=a11a33+a11a22+a22a33-a23a32，θ3=a11a22a33+a11a23a32+a13a21a32.

接着，考虑当τ=0 时系统（2）的稳定性，易得如下引理.

引理2如果τ=0 且θ1＞0,θ2＞0,θ3＞0,则系统（2）是渐近稳定.

证明当τ=0 时，由系统（5），可得

当θ1＞0,θ2＞0,θ3＞0 条件成立时，则方程（13）的特征根λi(i=1,2,3)满足根据引理2，如果τ=0，易得系统（2）是渐近稳定的.

为了给出我们的主要结果，进一步假设：

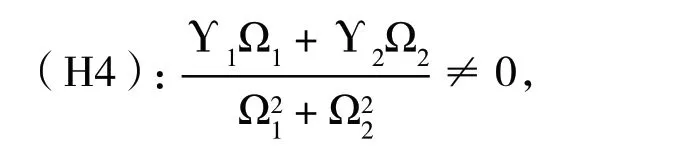
其中，Υ1=ω0(A2sinω0τ0-B2cosω0τ0),Υ2=ω0(A2cosω0τ0+B2sinω0τ0),Ω1=A′1+(A′2-τ0A2)cosω0τ0+(B′2-τ0B2)sinω0τ0,Ω2=B′1+(B′2-τ0B2)cosω0τ0(A′2-τ0A2)sinω0τ0.

引理3设s(τ)=ν(τ)+iω(τ)是方程（6）在τ=τj附近满足ν(τj)=0,ω(τj)=ω0的根，则下列条件满足

证明由隐函数定理，在系统（9）中对τ微分，可得

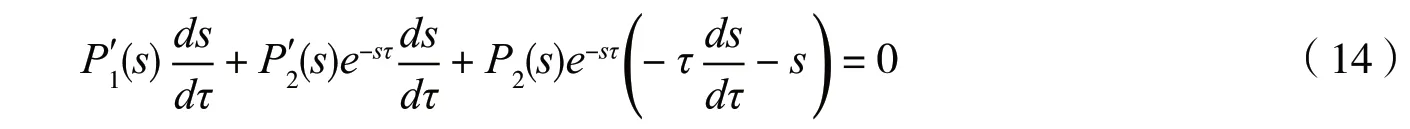
因此，我们有

其中，Υ(s)=sP2(s)e-sτ,Ω(s)=P′1(s)+P′2(s)e-sτ-τP2(s)e-sτ.

因此，可得

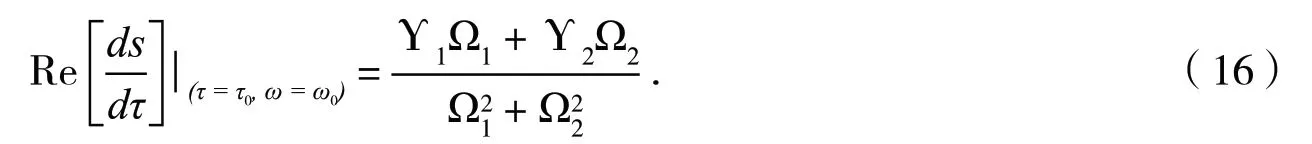
由（H3）可得，引理证毕.

基于上述分析，由引理3，可得如下定理：

定理1假如系统（2）满足：

（i）在假设（H1）～（H3）下，则平衡点对于τ∈[0,+∞)是全局渐近稳定的.

（ii）在假设（H1）～（H3）下，则：a）零点平衡点对于τ∈[0,τ0)局部渐近稳定；b）当τ=τ0时，系统（2）在平衡点处产生Hopf 分岔，即系统具有从τ=τ0附近的平衡点分岔的周期解.

2.2 带有反馈控制的Hopf分岔

通过上节讨论无控系统Hopf 分岔的存在性问题，因控制对系统起着重要作用，因此，下面在系统（2）的基础上增加状态反馈控制，系统描述如下：

其中φ1,φ2,φ3∈(0,1]是分数阶，Fi(i=1,2,3)是反馈控制算子.

为了讨论控制系统（17）存在Hopf 分岔的充分条件，类似上述的分析方法，先做平移变换，则控制系统变换为

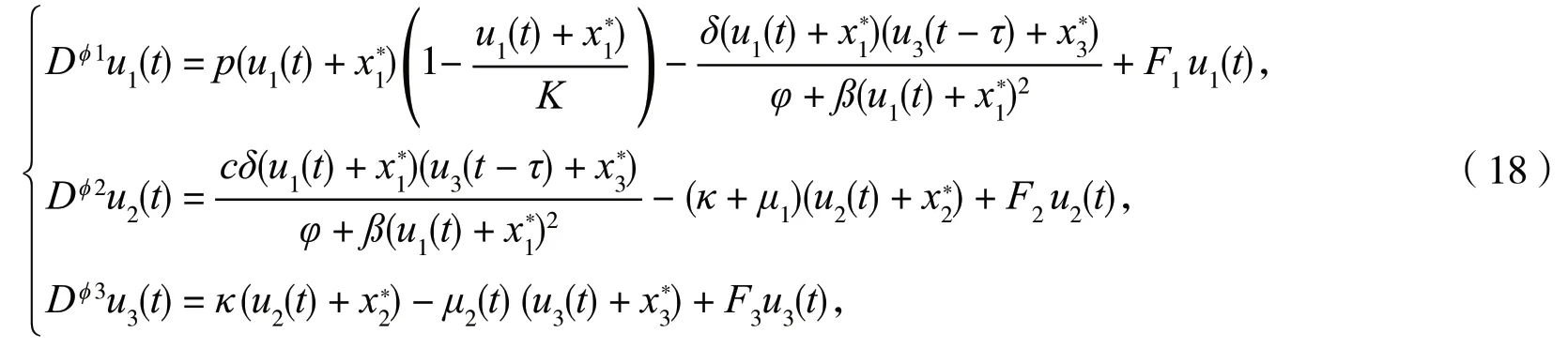
应用Taylor 展开进行线性化，可得

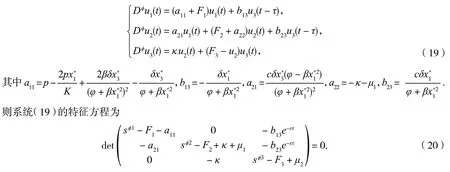
通过（20）我们可以得到

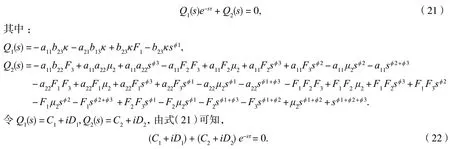
设s=iω=ω是方程（22）的一个根.将s代入式（22），分离其实部和虚部，可以得：

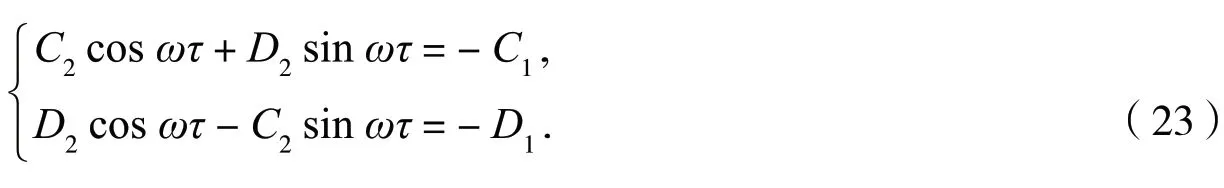
应用式（8）直接计算得到

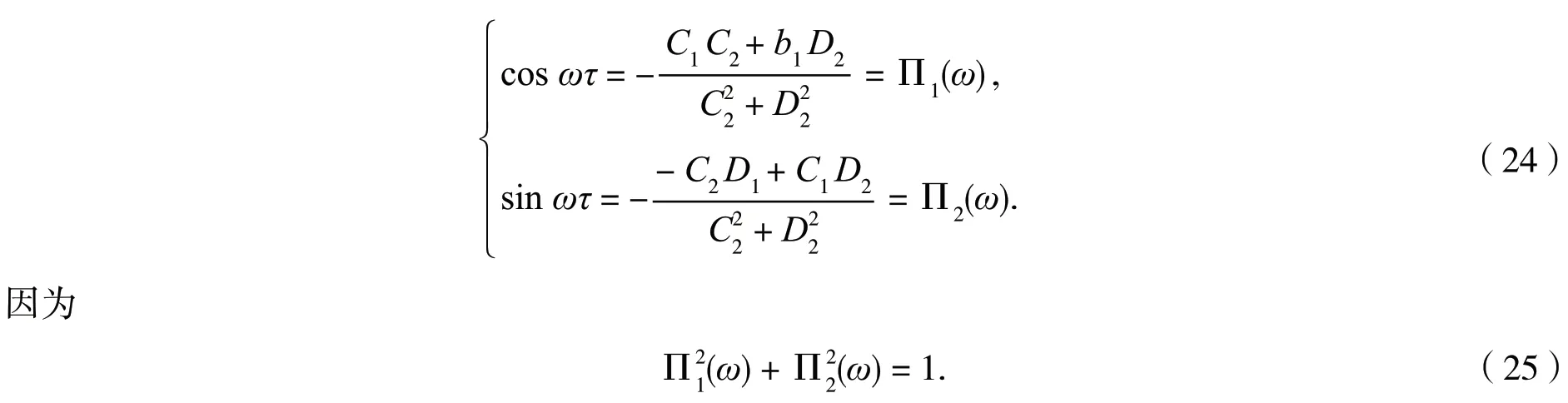
由于cosωτ=Π1(ω)，我们得到

定义分岔点

式（27）中，τ(κ)由式（26）给出.

为进一步得到主要结果，进一步假设如下条件成立：

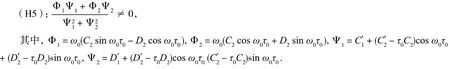
引理4设s(τ)=ν(τ)+iω(τ)是方程（6）在τ=τj附近的满足ν(τj)=0,ω(τj)=ω0的根，则下列条件成立

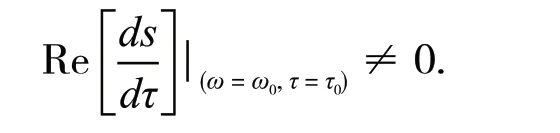
证明利用隐函数定理，在系统（21）中对τ微分，可得

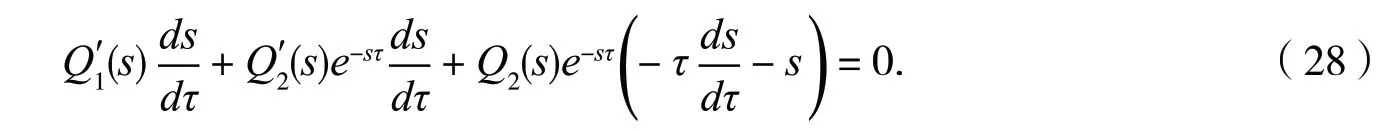
因此，我们有

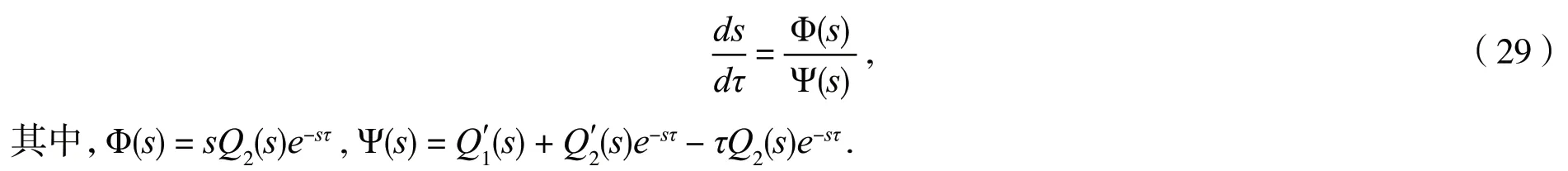
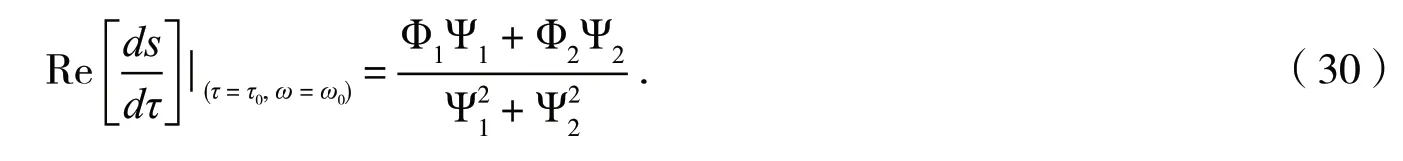
由（H5）可得，引理证毕.

基于上述分析，由引理3，可得如下定理：

定理2假如系统（17）满足：

（i）在假设（H1）～（H3）下，则平衡点对于τ∈[0,+∞)是全局渐近稳定的.

（ii）在假设（H1）～（H3）下，则：a）平衡点对于τ∈[0,τ0)局部渐近稳定；b）当τ=τ0时，系统（2）在原点处发生Hopf 分岔，即系统具有从τ=τ0附近的零平衡点分叉的周期解分岔.

3 数值模拟

在本节中，我们给出两个例子来证明所提方法的有效性.数值模拟基于Adama-Bashforth-Moulton 预估校正算法[18]，取步长Δt=0.01.

例1考虑下面的系统没有控制：

取分数阶φ1=φ2=φ3=0.9，初值为(x1(0),x2(0),x3(0))=(0.02,0.01,0.02).经计算得到ω0=1.167 5，则τ0=21.834 9.则定理1 中的（ii）成立.事实上，图1 显示，当τ=21 ＜τ0时系统（31）的零平衡点局部渐近稳定，而图2 则显示了系统（31）的平衡点呈周期震荡现象，也即，当τ=25＞τ0时发生Hopf 分岔.

图1 当τ=21＞τ0 时，系统（31）是局部渐近稳定的

图2 当τ=25＞τ0 时，系统（31）是周期震荡的

例2考虑如下时滞和控制的分数阶系统：

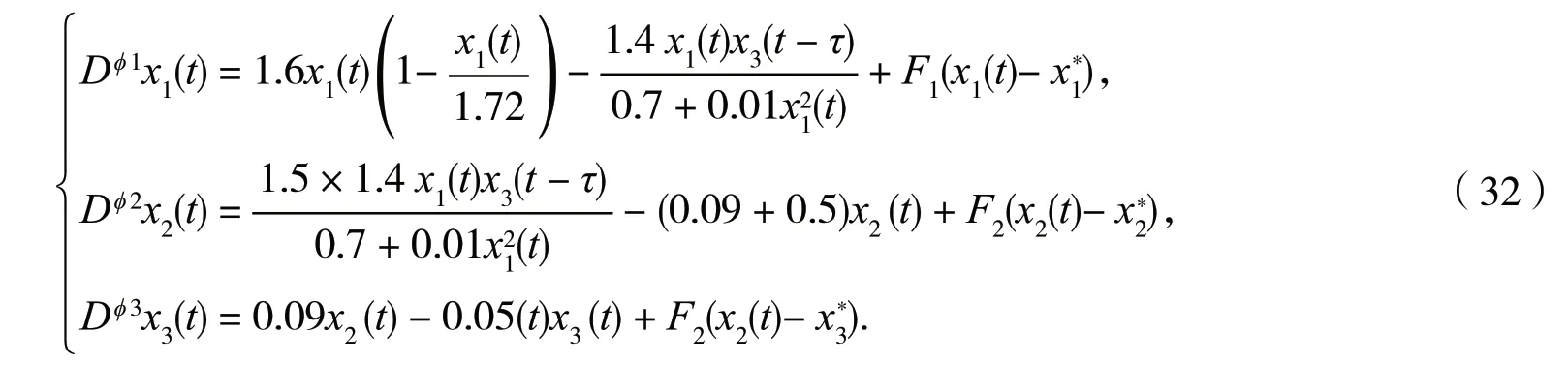
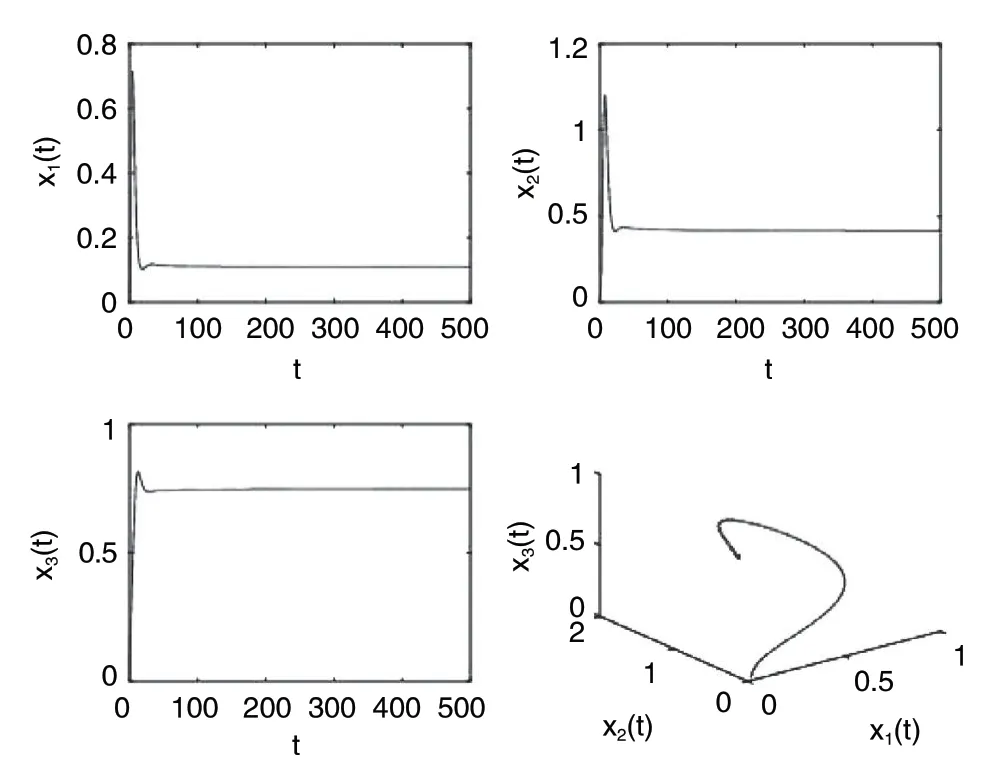
图3 当τ=40 ＜ τ0 时系统（32）是局部渐近稳定的

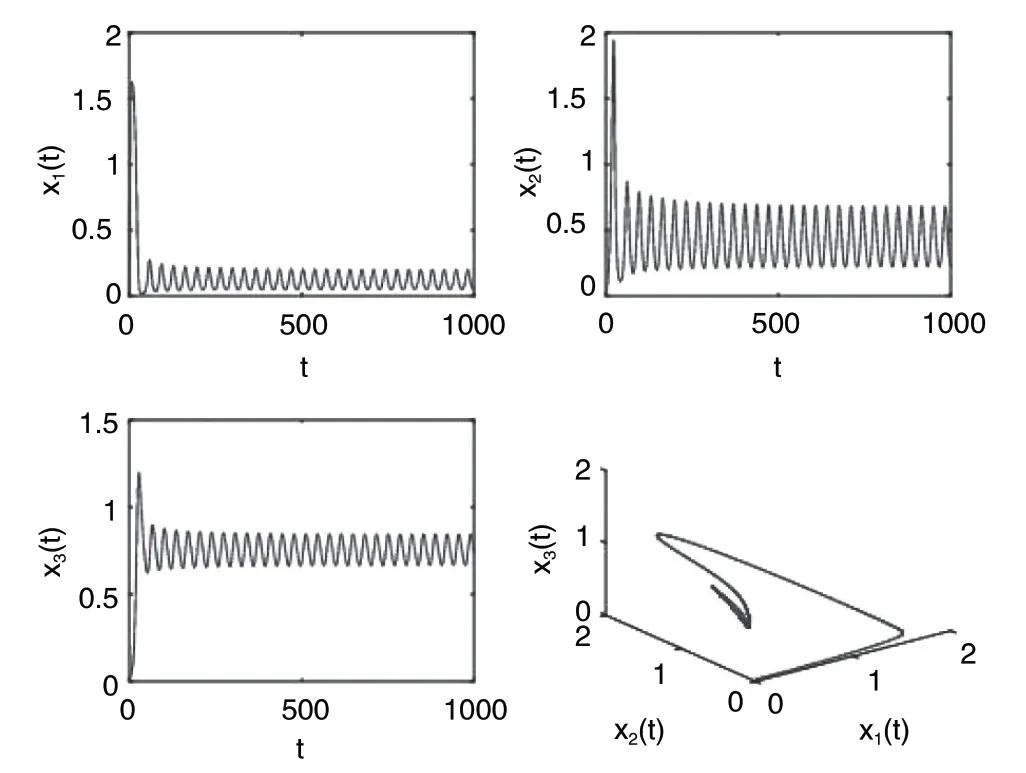
图4 当τ=50＞τ0 时，系统（32）是周期震荡的

4 结论

本文研究了一类具有时滞分数阶Lotka-Volterra 捕食-食饵模型的分岔问题.首先，通过对特征方程的综合分析，以时滞和分数阶为分岔参数，建立了时滞分数阶系统Hopf 分岔的稳定性判据.接着讨论了具有反馈控制的时滞分数阶Lotka-Volterra 模型的稳定性和分岔问题，并得到相应的分岔和反馈控制的存在严重地削弱了所提时滞分数阶Lotka-Volterra 捕食者模型的稳定性，最后通过两个数值算例说明所得理论结果的有效性.