保持双向等价关系的变换半群的一些结果

陈 辉，刘 鑫，王守峰

（云南师范大学 数学学院，云南 昆明 650500）

0 引言

设S是半群，E(S)是S中幂等元的集合.众所周知，格林关系L,R,H,D,J在半群理论中扮演重要角色.关于格林关系的定义和半群理论的相关概念可看参考文献[1].一个半群S称为纯正的，若E(S)形成S的子半群.半群S称为完全正则的，若它的每个H-类包含幂等元.

20 世纪70 年代，作为格林关系的推广，文献[2]研究了半群上的格林*-关系.半群S的L*和R*关系定义如下：

若a∈S且a所在的R*-类含幂等元，则称a是左富足元，对偶地，可定义右富足元.

1991 年，Lawson 引入了一种新的广义格林关系[3].设S是半群，定义S上关系～L和R～如下：

设X为非空集合，E是X上等价关系，T(X)是X上的全变换半群，X/E表示X的E-类的集合.从每个E-类中各取一个元素组成的集合称为E的一个截面.对任意α∈T(X)，α的核和像分别表示为kerα={(x,y)∈X×X|xα=yα}和Xα={(xα|x∈X}.设

许多学者对半群(X)作了研究.文献[5～7]研究了(X)上的格林关系及正则性.文献[8，9]研究了(X)的格林*-关系和富足性.文献[10，11]描述了(X)上的自然偏序.文献[12]则研究了(X)的变种半群上正则元的一些性质.

本文的目的是沿着这些方向继续研究半群(X).我们刻画了(X)上的关系，给出了=L*和R=R*的充要条件，证明了(X)中的正则元集Reg((X))形成子半群，得到了Reg((X))形成完全正则半群和纯正半群的充要条件.

1 预备结果

下面给出一些预备结果.

先给出TE*(X)上的格林关系.对

引理1[6]设（1）(α,β)∈L当且仅当Xα=Xβ；（2）(α,β)∈R当且仅当kerα=kerβ，|Z(α)|=|Z(β)|；（3）(α,β)∈H当且仅当kerα=kerβ，Xα=Xβ.

引理2[6]设α∈(X)，则α正则当且仅当对任意A∈X/E，有A∩Xα≠ ∅.也就是说，α正则当且仅当Xα含E的一个截面.特别的，若α是幂等元，则对任意A∈X/E，有Aα=A.

推论1设α∈(X)，R是E的截面，若α正则，则Rα也是E的一个截面.

证明任取r,s∈R，r≠s.则由α∈(X)知(rα,sα)∉E.另一方面，设x∈X，则由α正则及引理1.2 知存在y∈X使得(x,yα)∈E.由于R是E的截面，故存在r∈R使得(y,r)∈E，从而(yα,rα)∈E.于是(x,rα)∈E.这就证明了Rα是E的截面.

引理3[8](X)正则当且仅当|X/E|有限.

引理4[8]设α,β∈(X)（.1）(α,β)∈L*当且仅当Xα=Xβ；（2）(α,β)∈R*当且仅当kerα=kerβ；（3）α是左富足元.

引理5[4]设S是半群，a,b∈S，若a,b正则，则

若a,b为左富足元，则aR*b当且仅当

2 主要结果

本节给出半群(X)的一些新结果，先考虑(X)上的关系.

定理 1设α,β∈(X).则(α,β)∈当且仅当Xα=Xβ或者对任意所在E-类为{a}.

证明(⇐)若Xα=Xβ，则由引理4，下设Xα≠Xβ.任取e∈E((X)).设αe=α.任取x∈X.若xβ∈Xα，则存在y∈X，使得xβ∈yα.由αe=α知xβe=yαe=yα=xβ.若xβ∈XβXα，由条件知xβ所在E-类为{xβ}，由e幂等及引理2 知{xβ}e⊆{xβ}，即xβe=xβ.于是βe=β.对偶地，可证βe=β蕴含αe=α，故(α,β)∈

(⇒)设(α,β)∈则对任意e∈E((X))，αe=α当且仅当βe=β.假设Xα≠Xβ且存在(XαXβ)使得a所在E-类至少有两个元素.不妨设a∈XβXα，A∈X/E且a,c∈A.由a∈XβXα知，存在b∈X使得a=bβ.定义X上的变换e如下：

则e∈(X)且e2=α.显然，αe=α.然而，bβe=αe=c≠a=bβ，这与(α,β)∈矛盾.

由引理1 和4 知，L=L*.下面给出L*=和R=R*.的充要条件.

定理2在(X)中，L*=当且仅当|X/E|有限或者|X/E|无限且每个E-类至少含2 个元素.

证明(⇐)若|X/E|有限，由引理3 知(X)正则，从而由引理5，L*=.设|X/E|无限且每个E-类至少含2 个元素.若(α,β)∈，则由定理1 知Xα=Xβ.据引理4，

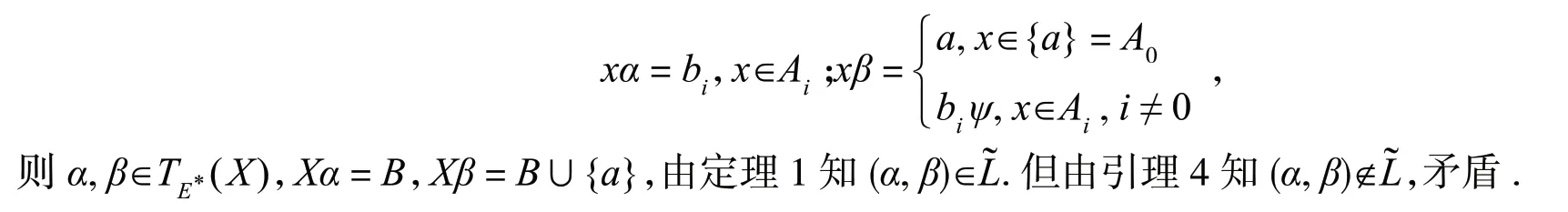
定理3在(X)中，R=R*当且仅当|X/E|有限.

证明若|X/E|有限，由引理3 知(X)正则，从而由引理5，R=R*.反之，设R=R*，则由引理4 知中每个元均为左富足元，即每个R*-类均含幂等元，从而每个R-类均含幂等元，于是正则.

定理 4设α,β∈(X)，α,β正则，则αβ正则.即Reg((X))形成正则子半群.

证明因为α正则，由引理2，Xα包含E的截面.又β正则，由推论1 知Xαβ也包含E的一个截面.再次利用引理2 知αβ正则.

下面给出Reg((X))完全正则的充要条件.

定理5Reg((X))完全正则当且仅当下列条件之一成立：（1）E为相等关系；（2）存在唯一的一个E-类含2 个元素，其余E-类均为单点集.

证明(⇒)对任意α∈(X)，由引理1 知，

假设（1）（2）均不成立，则有两种情况需要考虑.

情况一：假设存在两个非单点集的E-类A1,A2.不妨设A1={a1,b1,…}，A2={a2,b2,…}.定义X上的变换α如下：

由引理2 知

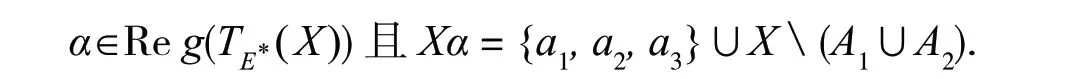
若存在e∈E((X))且e∈Hα，则Xα=Xe，kerα=kere.由引理2 得A1e={a1}，A2e⊆{a2,b2}.但这导致(a1,b1)∈kere=kerα，矛盾.故Hα中无幂等元.

情况二：假设只有一个非单点集E-类A，但该类元素个数大于2.不妨设A={a,b,c,…}，定义X上的变换α如下：

(⇐)假设E为相等关系，则(X)={σ | σ是X上的单射变换}.设α∈(X).若α正则，则由引理2知Xα包含E的一个截面，但E的截面只有X，从而Xα=X.这表明α是双射.于是αH1X.假设存在唯一的一个E-类A含2 个元素，其余E-类均为单点集.不妨设A={a,b}.对任意的α∈Reg((X))，由引理2知Xα包含E的一个截面.于是(XA)⊆Xα.若，定义幂等元e如下：

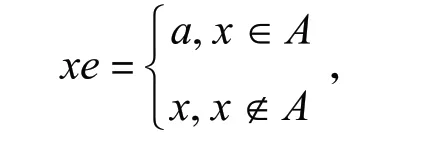
则αHe.若，定义幂等元f如下：

则αHf.若Xα=X，则αH1X.

综上所述，Reg((X)完全正则.

下面给出Reg((X))纯正的充要条件.

定理6Reg((X))是纯正半群当且仅当每个E-类至多含2 个元素.

证明(⇒)假设某个E-类A含元素多于2 个，取a,b,c=A.定义X上的变换e,f如下：

易证e,f∈E(TE*(X)),cef=a≠b=c(ef)2.故ef≠ (ef)2，从而Reg((X)不纯正.

(⇐)设X的每个E-类至多含2 个元素，e,f∈E((X))，由引理2 知对任意A∈X/E，有Ae⊆A，Af⊆A.设x∈X.若x所在的E-类为{x}，则必有xe=x=xf.从而xefef=x=xef.若x所在的E-类不是单点集，则存在唯一的y∈X使得x所在的E-类为{x,y}.于是{x,y}e⊆{x,y}.注意到e幂等，有以下三种情况：xe=x,ye=y或xe=x=ye或xe=y=ye.同理可知，xf=x,yf=y或xf=x=yf或xf=y=yf.于是有以下9 种情况：

（1）xe=x,ye=y,xf=x,yf=y；（2）xe=x,ye=y,xf=x=yf；

（3）xe=x,ye=y,xf=y=yf；（4）xe=x=ye,xf=x,yf=y；

（5）xe=x=ye,xf=x=yf；（6）xe=x=ye,xf=y=yf；

（7）xe=y=ye,xf=x,xf=y；（8）xe=y=ye,xf=x=yf；（9）xe=y=ye,xf=y=yf.

对情形1，有xef=yf=x,xefef=xef=x.对情形2，有xef=yf=x,xefef=xef=x.

对情形3，有xef=xf=y,xefef=yef=yf=y.类似可证后面几种情形.

综上所述，(ef)2=ef.于是是纯正半群.