一类三角形数转化成正方形数的充要条件及算法研究

赵美利，唐 静

（滁州城市职业学院，安徽 滁州 239000）

三角形数和正方形数是数学中一类有趣的问题,我们熟悉的古希腊数学家毕达哥斯拉就提到过三角形数和正方形数[1]，把数看作点集或点状物体，把数字和图形联系在一起，将正整数和正方形、正五边形、三角形等联系起来，将数字划分为正方形数、五边形数、三角形数等，会使数字更加形象生动，研究其规律也更方便.之后，很多人对此问题进行了讨论和研究，得出了一些特殊的三角形数和正方形数，所有大于3的三角形数都是合数，所有三角形数的倒数之和是2，任何一个完全平方数都可以表示成相邻的两个三角形数之和[2].郑玉美利用余弦定理从120°三角形数方面得出了两个性质[3].张爱静从三角形数和数三角形角度讨论了三角形的一些规律，得出了数与规则图形的一些结论[4].黄祎利用初等方法和解析方法，首次提出了三角形数和数列的关系，研究Smarandache 三角形数的下部及上部数列的几何平均值的极限问题[5].智婕在佩尔方程x2-py2=1 的求解技巧一文中把佩尔方程和三角形数建立了联系，利用佩尔方程的解的规律得到了满足一定条件的特殊的三角形数[6].余熙国得出关于三角形数和正方形数的一个结论，一个正整数既是三角形数也是正方形数有无限多个，可以用通式表示，给出了三角形数和正方形数的关系，但是没有给出两者相互转化的结论[7].近年来很多中学都注重培养学生思维能力和创新能力，在数学学科竞赛题中经常出现三角形数的考题，吴家华将一个数列的各项重新排列，构造三角形数阵，妙解一类数列问题，提出了三角形数的应用问题，开辟了新的领域[8].

综上所述，对于这个有趣数学的问题，人们已对其进行了诸多的探讨并形成了一定的结论，但是对于三角形数和正方形数的转化问题目前尚没有涉及到.为了更进一步探讨两者的本质联系，本文对满足一定条件的三角形数如何转化成正方形数进行研究.

1 预备知识

三角形数：将物品以三角形形式等距离排列，可以形成等边三角形，这样得到的物品的数，比如1，3，6，10，15，21，…，这样的数称为三角形数.

正方形数：正方形数也称平方数，将一定数量的点或圆等距离排列成正方形，这样得到一组数，比如1，4，9，16，…，这样的数称为正方形数.

数列：按一定顺序排列的一列数叫数列；用{an}表示，其中n是项数，an=f(n)是通项公式.

求和公式：若数列{an}是等差数列，求和公式，其中a1为首项，d是公差.

佩尔方程：形如x2-dy2=1(x,y∈Z+;d不是平方数)方程称为佩尔方程，其满足方程的正整数解是初等数论经典问题之一.

2 相关结论

自从三角形数作为一类特殊的数，有一定的规律之后，人们开始一系列探讨和研究，比如三角形数的第n个数是，所有的三角形数的倒数之和等于2，任何两个相邻的三角形数之和都是一个正方形数，等等.三角形数是否化为正方形数，是一古老有趣的数学问题，也是初等数论的经典问题之一，在不少书刊和中学生数学竞赛中出现.笔者经研究发现，若三角形数可化为正方形数，只要满足一定条件即可，从而对解决这一古老有趣的数学问题提出了一个参考性的路径，下面我们进行一些分析、讨论.

引理1设an为三角形数的第n行的正整数，构成新的数列为{an}，若an+2=6an+1-an+2a1=1，a2=8，则

证明因为{an}有递推公式an+2=6an+1-an+2，

虽然选派业务工作人员下基层到各县级图书馆进行专业指导、培训产生了一定成效，但由于人力、物力、以及时间有限，难以做到面面俱到。笔者认为，应该以点带面，可参照现行许多如美丽乡村建设、红旗示范岗、精神文明单位等示范点的做法，在全面开展文化扶贫工作的同时，先重点选择一两个有代表性的基层图书馆作为示范点单位，加大力度为其提供人力和技术支持，使其作为示范性图书馆，发挥引领性作用。

设bn+2-αbn+1=β(bn+1-αbn)，则bn+2=(α+β)bn+1-αβbn.

由（1）式知α+β=6，αβ=1，求解方程组得到的解为

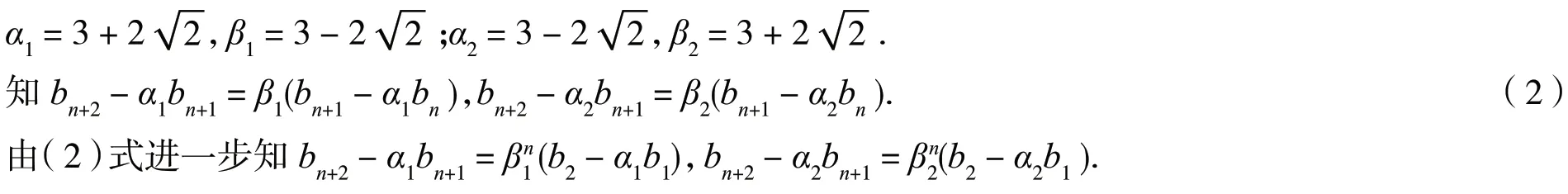
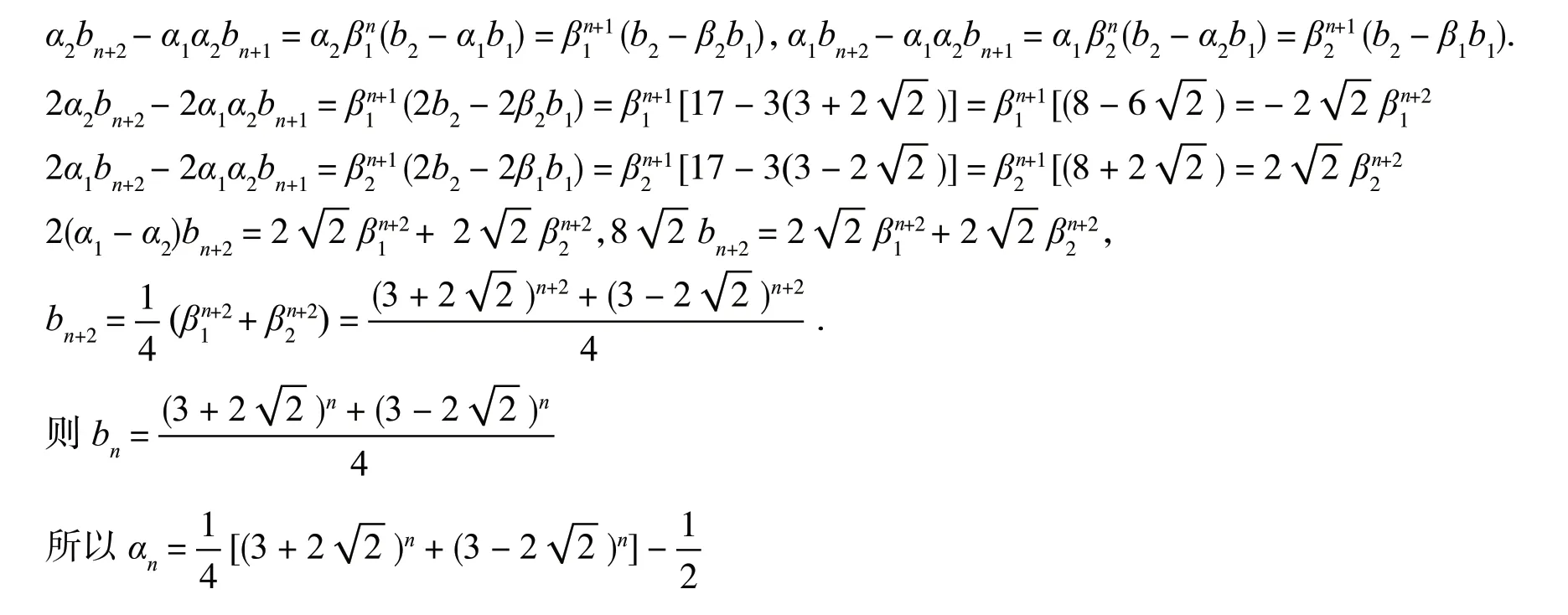
综上所述引理1 得证.

我们经过数列的性质进一步推导后就会发现，对引理1 的数列各项进行求和，会有更一般的结论，下面给出这个结论，并给出证明.

综上所述引理2 成立.

由以上两个引理我们得到三角形数转化成正方形数的充要条件，下面我们给出结论，并利用佩尔方程简单证明这个结论是正确的，从而解决了三角形数和正方形数互相转化的这一初等数论的经典问题.

定理如三角形数可化为正方形数，三角形数第n行的正整数为an，则

证明∵三角形数可化为正方形数，第n行的正整数为an，由引理2 知

∴存在相对应的正整数mn，使得

由佩尔方程的概念易知（4）式符合佩尔方程形式.

由佩尔方程的通解知（4）式的通解为

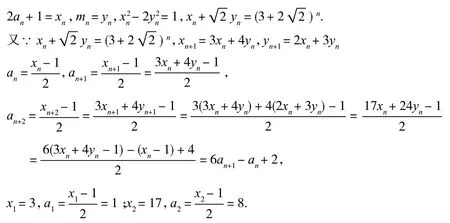
知an+2=6an+1-an+2，a1=1，a2=8.

定理得证.

由引理1 和引理2 知定理结论是正确的.

此定理给出了三角形数和正方形数转化的充要条件，彻底解决了两者之间的联系问题，以前只是片面的讨论三角形数和正方形数的规律问题，形成了一定的结果.所以研究此问题很有必要，有一定的理论指导意义.此定理是对原来三角形数判定定理的延拓，更具有一般性和使用的广泛性.为进一步证明其结果的准确性，利用java 中大整数的特点设计相应的算法并验证其结论的正确性.

3 算法实现

程序设计语言基本数据类型中long 类型所能表示的整数范围是最大的，但还是有限的.当数据值超出范围会有异常出现，而Java 中专门提供了用来进行不限制大小的整数计算的类——java.math.BigInteger.支持任意精度的整数，可以准确地表示任何大小的整数值，而不会丢失任何信息[9].在该类中封装了大整数相加add()；相减subtract()；相乘multiply()；相除取整divide()；取余remainder()；求幂pow()；a.pow(b)=a^b；最大公约数gcd()；绝对值abs()；是否相等boolean equals()；通过使用这些大整数运算，可以求解许多高精度运算问题.在本算法中需要验证通过公式所得数列中的每个数是否是完全平方数（正方形数）和对完全平方数取得其平方根，在java.math.BigInteger 类没有这两种方法，需要自己设计.以下两种算法就是完全平方数和取得其放平方根的设计.

（1）//public static BigInteger myBigNumSqrt(BigInteger xx){}方法是对大整数求平方根

（2）//public static BigInteger is_square(BigInteger F7){}方法是判断大整数是否是完全平方数

该算法利用数组长度为102 最终实现的结果如下求数列αn的值：

求数列b的值即的值：三角形数

求数列完全平方数：

求数列b每个数开方之后的值：

在Eclipse 开发环境下该程序运行的结果界面如下

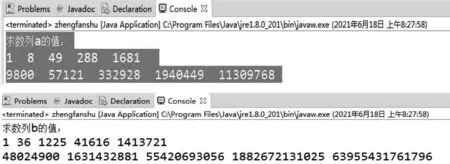
图1 程序运行的结果界面

4 结语

本文讨论了三角形数和正方形数的转化的充要条件，在此基础上用Java 语言中大整数的特点和大数据分析方法对三角形数和正方形数以及正多边形数进行分析和编写语言程序，但对于这种算法的实现也是永无止境的课题.当然，三角形数和正方形数的判定条件还可以进一步优化，还需要我们进一步去研究和发现.

此外，三角形数和正方形数的判定问题是初等数论讨论的经典问题之一，对于它们的求解问题一直是近年来竞赛题的重要选题，对其进行探讨，对培养学生的创新思维能力也有一定积极意义.