混合滤波器优化的雷达信号调制识别算法

高敬鹏， 毛新蕊， 吴若无， 卢毅

(1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001； 2.电子信息系统复杂电磁环境效应国家重点实验室，河南 洛阳 471003)

随着信息化产业推进，电子战逐渐成为现代战争的主要作战方式。雷达信号调制识别作为电子侦察的关键技术，在电子战中占据着核心地位[1]。目前，电子战所处环境往往复杂多变，雷达信号调制识别愈发困难[2]；人工智能的发展使深度学习逐渐在雷达信号调制识别领域崭露头角，然而非合作性质使雷达数据难以采集，无法满足训练对样本数量的要求。因此，如何在少量样本条件下实现雷达信号调制精确识别成为亟待解决的技术难题。

雷达信号调制识别关键在于合理提取特征[3]。常规辐射源信号都是非平稳的，传统单一域分析方法难以获取充分特征信息。文献[4]将时频图像的中心矩和伪Zernike矩作为特征进行固定提取，使其表征能力得到一定提升，但仍存在误判风险。近年来，卷积神经网络(convolutional nneural networks，CNN)在特征提取方面大放异彩，能有效克服固定特征提取的局限性，但仍存在计算量大，难以训练的问题[5]。侯坤元等[6]搭建CNN模型实现了信号调制识别，但其设计的网络结构及训练所需计算量巨大，难以满足实际计算性能要求，Chan[7]等构造一种主成分分析网络(principle component analysis network，PCANet)，基于空间映射思想设计滤波器，替换传统意义的卷积核，提取图像特征，保证网络精度的同时降低网络复杂度，为雷达信号调制识别提供思路。文献[8]设计双通道网络融合图像的多分辨率特征，也能达到较好识别效果。因此，通过引入特征融合思想，可以增强信号表征能力，进一步提升雷达信号调制识别效果。

另一方面，若要利用所获特征实现有效辨识，分类器的选取与设置也尤为重要。支持向量机(support vector machine，SVM)是一种适用于样本数少的机器学习算法[9]，但其参数设置不当会使分类性能显著下降。目前，智能算法在参数优化方面取得了众多成果[10]，常见算法包括网格搜索法[11]、差分进化算法[12]、粒子群优化算法等[13]。网格搜索法对目标函数要求不高，但计算量偏大，且算法精度偏低；差分进化算法全局性较好，但收敛速度较慢；粒子群优化算法收敛速度快，但局部性能较差。上述算法在不同程度上满足SVM组合控制参数优化需求，但在全局与局部性能平衡、简易性和计算精度上仍有欠缺。Sankalap等[14]提出了一种蝴蝶优化算法(butterfly optimization algorithm，BOA)，该算法参数少，易于实现，且速度明显优于网格搜索法、差分进化算法和粒子群优化算法，然而也存在易陷入局部最优的问题。本文在BOA算法上结合全局性好的差分进化算法，优化SVM参数，进一步提高调制识别效果。

本文受PCANet和融合思想的启发，提出一种混合滤波器优化(hybrid filter optimization，HFO)的雷达信号调制识别算法，将降维与融合思想相结合，设计混合滤波器，构建一种结构类似PCANet的简单卷积网络，提取图像多角度特征；并提出混合蝴蝶优化算法(hybrid butterfly optimization algorithm HBOA)寻优SVM参数，解决雷达样数少时难以训练深层次网络参数的问题，提升调制识别率。

1 信号与系统模型

1.1 信号模型

在现代战场上，多种调制方式的雷达信号被广泛应用于战场以提高电子对抗过程中的侦察和干扰能力，为此本节给出了雷达调制信号的数学模型为：

x(t)=s(t)+n(t)=

A(t)exp[j(2πf0t+c(t)+φ0)]+n(t)

(1)

式中：x(t)表示接收到的实际雷达信号；s(t)表示辐射源发出的实际雷达信号；n(t)表示噪声；A(t)表示幅度函数；f0表示载波频率；c(t)表示相位函数；t为采样时刻；φ0表示初始相位。雷达信号常用的调制方式有：CW、BPSK、LFM、COSTAS、FRANK、P1、P2、P3、P4，9种信号产生方式为[15]：

CW：

BPSK：

LFM：

COSTAS：

FRANK：

P1：

P2：

P3：

P4：

式中：A代表信号幅度；rect(t)为矩形函数；T为信号宽度；N代表码元数量；φi∈2π(m-1)/Ψ,1≤m≤Ψ；Ψ代表相位数；Tp为码元宽度；k为调频斜率；Tr为脉冲重复周期；u(t)代表子脉冲；fn为第n个子脉冲的频率；φi,j代表多相码第i个采样点在第j个步进的相位；i=1,2,…,M,j=1,2,…,M，M为多相码的相位数；Nc为压缩比。

1.2 系统模型

为提升样本数目少时的雷达信号调制识别率，本文提出混合滤波器优化的雷达信号调制识别算法，其系统模型如图1所示。首先，预处理截获雷达信号，采用Choi-Williams分布[16](choi-williams distribution，CWD)将其转换为时频图像。其次，利用多通道技术将时频图像转换为RGB三通道。再次，设计二级级联滤波器，第1级采用局部保留投影算法[17](locality preserving projections，LPP)设计滤波器，第2级分别运用LPP、PCA及线性判别分析[18](linear discriminant analysis，LDA)设计混合滤波器，结合哈希编码和直方图映射，构建特征值映射网络(eigenvalue mapping network，EMN)，据此提取图像特征向量。最后，结合群智能技术，利用变异与进化理论提出混合蝴蝶优化算法，优化SVM组合控制参数，完成特征分类，提高样本数少情况下的雷达信号调制识别效果。

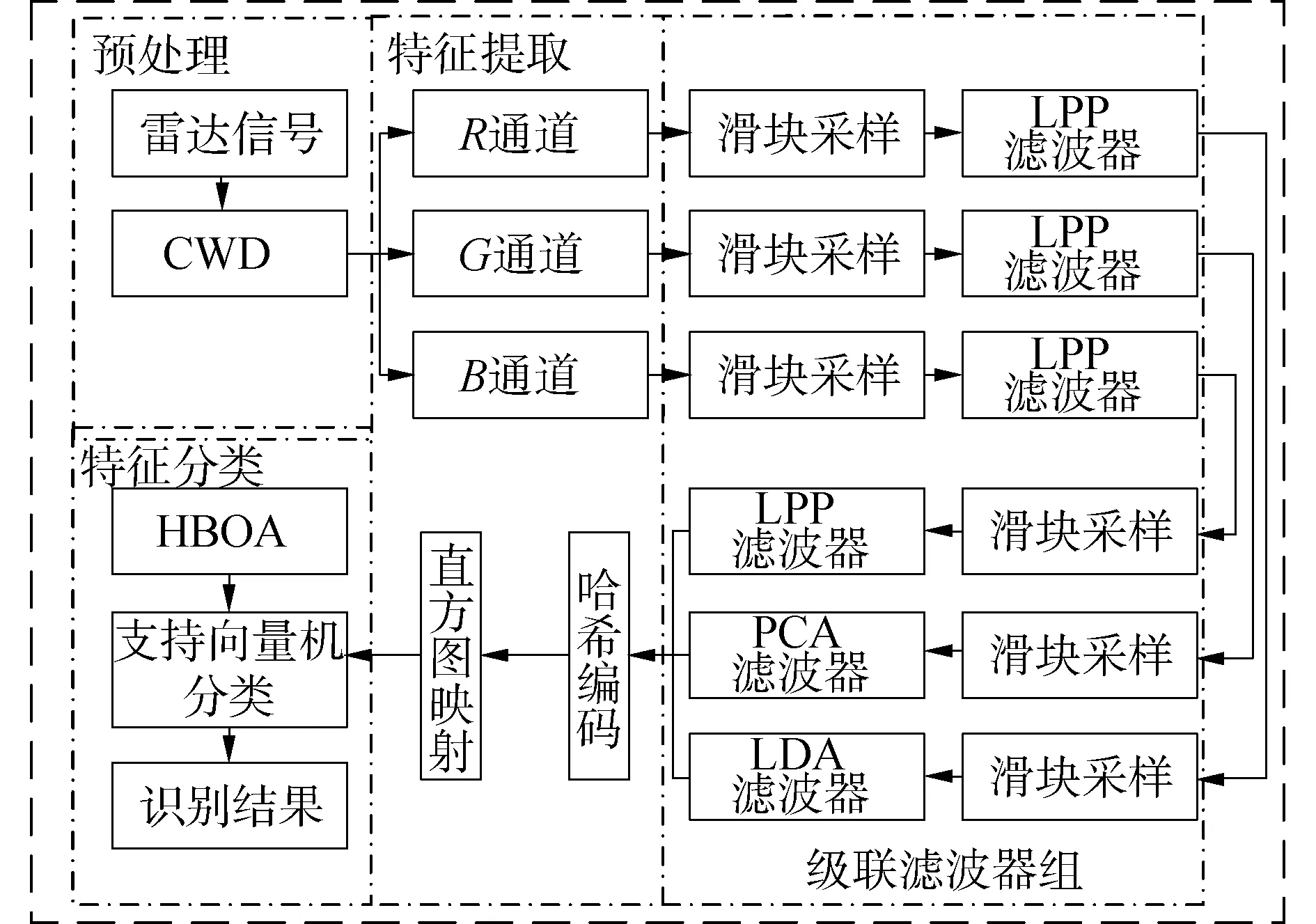
图1 调制识别系统模型

2 特征提取及分类

2.1 信号预处理

信号预处理可将雷达信号变换为更利于特征提取和识别的形式，CWD作为时频分析的一种手段，在面对非平稳信号时具备良好时频聚集性。CWD表达式为：

(2)

式中：Rs(u,τ)为雷达信号s(t)的自相关函数；exp[-(t-u)2×4-1η-1τ-2]为CWD的核函数；η为缩减因子。9种雷达信号时频分布示意图如图2所示，横轴表示时间，纵轴表示频率，可看出能量分布集中且无交叉干扰。不同信号对应时频图像形状和纹理略有不同，可用该特性提取图像特征来进行雷达信号调制识别。

图2 雷达信号CWD示意

2.2 特征提取

特征提取也就是如何从高维的图像数据中获取一些重要信息，是识别的一个重要过程。雷达信号由于非合作性质无法满足CNN参数训练要求，特征提取效果不佳，PCANet较之于传统的CNN来说，参数大大减少，训练过程简单，不需要反向传播调整权值系数，以其作为架构设计网络可以弥补CNN不足，获取理想识别效果。

2.2.1 基于单一滤波器的网络卷积层

然而当训练样本处于低信噪环境时，PCANet识别效果会受到影响。基于流形学习的非线性降维算法则表现优异，但其计算的映射空间与参与训练的数据有关，不具备泛化性。LPP算法可保持高维数据流形局部不变性，在低信噪比时表现良好，且具有获得新样本的低维投影的优良性质，具备较强泛化能力。本文利用LPP优化PCANet，设计二级级联滤波器，构建特征值映射网络。

在设计滤波器之前，先对输入图像块采样，降低计算难度。假设输入N个m×n大小的图像，令采样窗口大小为k1×k2，有重叠采集图像，去均值，可以得到数据矩阵：

(3)

式中：K为滑动的采样窗口；Ii为输入图像；*表示卷积。

获取数据矩阵后，设计LPP滤波器提取图像特征。LPP旨在学习数据类别信息和局部几何结构信息，目的是使重构误差最小化，并转换为求解特征向量的问题。LPP将最小化重构误差作为目标函数：

(4)

式中：t为给定参数；Sij为相似性矩阵，表示第i个矩阵与第j个矩阵间相似度；W=[w1,w2,…,wd]为所求投影矩阵，由如下广义特征值求解问题中最小特征值对应的前L1个特征向量构成：

XLXTw=λXDXTw

(5)

式中：matk1k2(wl)表示从wl∈Rk1k2映射到矩阵W∈Rk1×k2的函数；L1为第1级滤波器数量。式(5)由前L1个最大特征值对应的特征向量构成。获取特征值映射矩阵作为滤波器，与数据矩阵卷积。则可以得到第1级第l个滤波器输出：

(6)

由式(3)～(6)可以看出，基于单一滤波器的网络不需CNN的反向传播过程，可以有效解决少量样本情况下难以训练卷积核参数的问题。但是基于单一滤波器的卷积层未考虑不同通道之间差异性，对彩色图像3个通道均用相同滤波器提取图像特征会降低其表征能力，影响有限样本数情况下雷达信号调制识别效果。

2.2.2 基于混合滤波器的网络卷积层

为提升少量样本时雷达信号调制识别率，本文优化单一滤波器，设计混合滤波器提取图像多角度特征，利用多通道技术融合特征信息，增强其完备性。基于二级级联混合滤波器的EMN结构如图3所示。

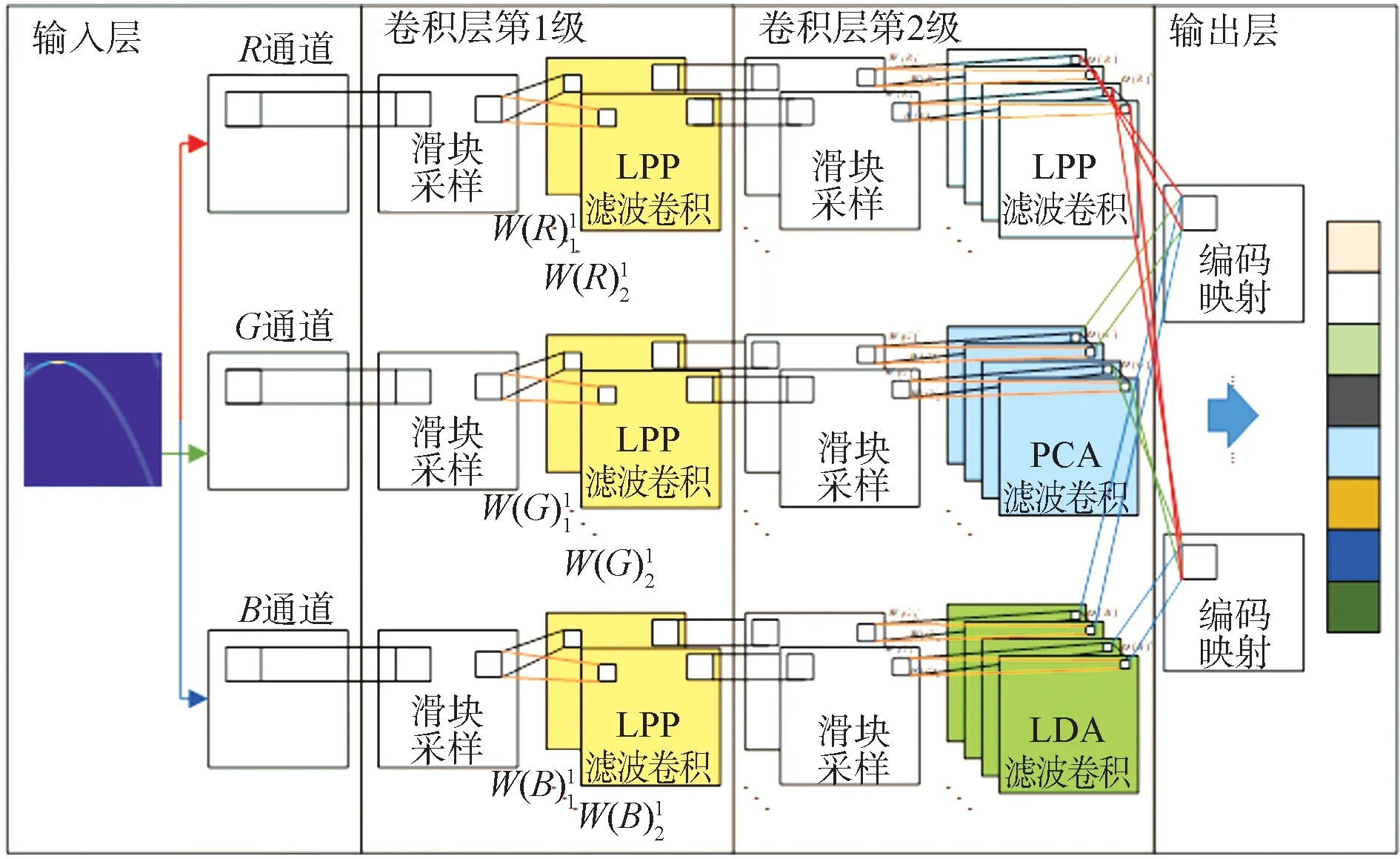
图3 特征值映射网络结构

(7)

(8)

对于R通道分量，采用LPP设计滤波器系数为：

(9)

式中：L2为第2级滤波器数量。R通道分量经二级滤波卷积后输出为：

(10)

对于G通道分量，用PCA设计滤波器，其目标函数为：

(11)

对式(11)求解即转化为计算Y(G)Y(G)T特征值，利用式(9)将L2个特征值对应特征向量作为滤波器，则G通道分量经二级滤波器卷积后输出可表示为：

对于B通道分量，采用LDA降维算法计算滤波器系数。LDA为有监督降维方式，是有类别输出，它的思想是使投影后类内方差最小，类间方差最大，更有利于后续分类。该思想借助方差波动表达，而散度矩阵与方差波动等价。假设样本有C类，样本的类内散度矩阵Sw和类间散度矩阵Sb为：

(12)

式中：yk表示第i类样本中的第k个向量；μi表示第i类样本的均值向量；mi表示第i类样本的数量；μ表示所有样本的均值。

LDA的核心是最小化类内散度并最大化类间散度为：

(13)

引入拉格朗日条件极值为：

L(W,λ)=WTSbW+λWTSwW

SbW=λSwW

(14)

(15)

利用式(4)、(11)和(13)，LPP提取数据局部几何结构和类别特征，与此类似，PCA和LDA分别提取整体特征和分离性强的特征，将三通道输出特征拼接，实现特征融合为：

(16)

融合滤波器所提特征，丰富信息多样性，有助于增大雷达信号时频图像的表征能力。

2.2.3 网络输出层

考虑到混合滤波器提取的特征矩阵冗余信息过多，不适合直接送入SVM完成识别，Chan等[7]利用哈希编码和直方图映射技术在不降低识别精度的情况下减少全连接参数，进一步压缩网络，将特征矩阵转变为可用于SVM形式的特征向量，同时降低处理难度，提高了特征纯度。因此本文采用同样方法设计EMN的输出层，以优化混合滤波器提取的多角度特征。

网络输出层主要包含二进制哈希编码与直方图映射，首先对输出特征二值化：

(17)

式中H(·)为阶跃函数。接着对L2个二值化后图像加权求和：

(18)

式中：l=1,2,…,L2。

完成哈希编码后，采用直方图统计法将其转化为特征向量。将一个求和得到的矩阵划分为块，所有块上的直方图统计向量级联，获取输入图像特征向量：

(19)

2.3 特征分类

提取特征后，通过分类器实现雷达信号调制识别。在非合作的雷达对抗环境中，雷达信号样本数目少，SVM可解决有限样本下的分类问题，但性能在很大程度上取决于其参数，群智能优化算法依靠群体间共同协作完成参数寻优等复杂任务。本文针对SVM组合控制参数选取不当导致识别率下降的问题，提出混合蝴蝶优化算法，引入柯西变异算子，结合差分进化思想，提升SVM识别性能。

2.3.1 支持向量机

SVM利用非线性映射处理待分类样本数据，在高维特征空间内寻找最优分类超平面，最终提高目标识别率，且SVM在少量样本情况下识别结果具备一定鲁棒性，有较强泛化能力，因此选取SVM作为分类器实现少量样本调制方式识别。它的基本思想是：用内积函数定义非线性变换，将输入空间从低维变到高维空间中，使样本线性可分。径向基函数(radial basis function，RBF)在SVM分类中具备良好特性，且对于少量样本情况下分类效果好，它通过调节参数增加灵活性：

(20)

式中σ为核函数的参数。

SVM的目标函数为：

(21)

式中：w代表分类超平面法向量；C>0代表SVM的惩罚因子；ξi代表松弛变量；b∈R代表阈值。SVM最终的决策函数可以表示为：

f(x)=sgn[(w·φ(x))+b]=

(22)

SVM核函数参数σ与惩罚因子C的取值会决定分类器性能：σ值过大时容易过拟合，过小时会出现欠拟合；C越大，对错分类惩罚越大，对训练集测试时识别率越高，但泛化能力弱，C越小，对误分类惩罚减小，泛化能力较强。因此，合理选择组合控制参数对分类器性能有至关重要的影响。

2.3.2 蝴蝶优化算法

BOA算法是一种新型群智能优化算法，由自然界中蝴蝶觅食和求偶行为衍生而来，具备涉及参数少、收敛速度快等优点，故本文采用蝴蝶算法优化SVM组合控制参数。蝴蝶行为可以描述成向食物源位置的协同运动，蝴蝶感知空气中香味，确定食物的所在位置。每只蝴蝶产生与适应度值相关的香味，当蝴蝶从一个位置移动到另一个位置时，适应度会相应变化。

在BOA中，每种香味代表其独特的感知能力，蝴蝶产生香味的数学公式为：

f=cIα

(23)

式中：f为香味被其他蝴蝶感知的强度；c为感觉模态；I为刺激强度；α为依赖于香味的幂指数，代表吸收的变化程度，一般情况下c和α取[0,1]内的随机数。

BOA有3个阶段：初始化阶段、迭代寻优阶段和最终阶段。在初始化阶段，定义目标函数、解空间及一些参数。初始化结束后，蝴蝶进入迭代寻优阶段，在每次迭代中，每只蝴蝶位置均改变。首先计算解空间中不同位置上蝴蝶的适应度值，然后按式(23)计算它们在当前位置产生的香味，按照切换概率P选择蝴蝶处于全局搜索阶段还是局部搜索阶段。在全局搜索阶段，蝴蝶朝最优位置移动，更新公式为：

(24)

(25)

2.3.3 混合蝴蝶优化算法

BOA算法涉及参数较少且易于实现，在求解速度方面明显优于网格搜索法、粒子群优化算法等经典智能算法，但蝴蝶个体间缺乏信息交互，且搜索位置有限，导致蝴蝶算法存在种群多样性差、易陷入局部最优的问题。变异策略可以生成新个体，扩大搜索范围，增强种群多样性，另外，通过引入交叉机制，可有效提高蝴蝶的信息交互能力，进一步提升算法全局寻优性能。因此，针对BOA算法种群多样性不足、易陷入局部最优等缺陷，本文提出HBOA算法，利用柯西变异算子修正全局位置，并引入差分进化算法的交叉变异机制，优化蝴蝶算法位置更新机理，提高BOA全局寻优性能。为将HBOA算法用于待优化问题中，将蝴蝶位置与可能解[C,σ]对应，适应度函数根据SVM模型识别率确定，并根据适应度值评价蝴蝶个体位置的香味，求解SVM组合控制参数。

HBOA算法主要针对蝴蝶优化算法易陷入局部最优的问题。首先将雷达信号调制识别率作为HBOA算法的适应度函数，定义为：

(26)

式中：D表示训练样本总数；ξ(i)为正确标签数量：

式中：Θ(i)为第i个训练样本标签；τ(i)为第i个预测样本标签。定义适应度函数后，改进蝴蝶位置更新方式。

鉴于蝴蝶算法全局寻优能力较差，而柯西变异具备较强的扰动变异能力，可帮助蝴蝶跳出局部最优，本文利用柯西变异算子修正全局最优个体：

(27)

式中：∂为引入柯西变异算子后的蝴蝶位置：

(28)

式中：λ(0,1)是柯西分布函数；l为0～1均匀分布的随机数；PA为随机变异概率。

尽管修正全局位置能够提升蝴蝶算法全局寻优能力，蝴蝶的局部位置仍然存在搜索位置受限的问题，需进一步改进。差分进化(differential evolution，DE)算法利用不同个体间信息交互丰富、种群具有多样性，是一种有效的全局优化算法。本文在局部搜索阶段，利用差分进化算法中变异行为，对整个种群实施交叉操作，改变位置更新方式，进一步增大种群多样性，提升SVM性能。

在第t次迭代中，以一定概率从种群中随机选择3个两两不同的个体xr1、xr2和xr3使蝴蝶产生变异：

(29)

式中：F为缩放因子，通常情况下取0.5。交叉变异后的新个体与当前个体新的蝴蝶位置为：

(30)

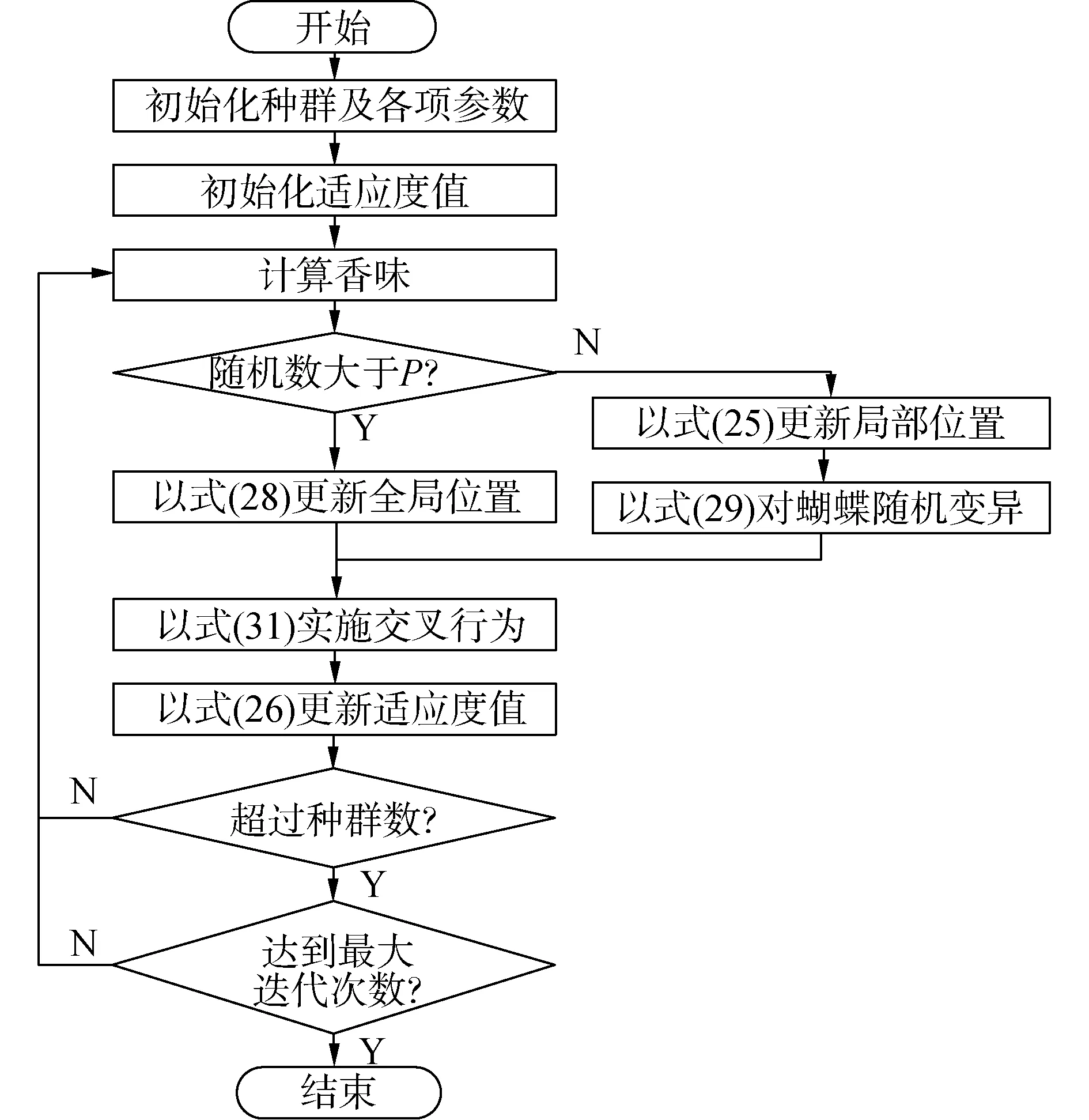
图4 HBOA算法流程

1)初始化蝴蝶种群及各项参数。随机初始化SN个二维蝴蝶位置，代表要优化的参数；

2)计算适应度值。将初始化蝴蝶位置作为SVM参数，根据式(26)计算初始适应度值；

3)根据式(23)计算蝴蝶产生的香味；

4) 更新蝴蝶全局位置。根据式(28)，结合步骤3)产生的香味更新全局变异蝴蝶位置；

5) 更新蝴蝶局部位置。根据式(25)、(30)，结合步骤3)产生的香味更新局部变异蝴蝶位置；

6) 实施交叉操作。根据式(31)对整个种群实施交叉操作，实现蝴蝶个体间的信息交互；

7) 根据式(26)计算蝴碟适应度值，并与原适应度值比较，保留适应度值更大的蝴蝶位置；

8) 判断是否达到最大迭代次数，若未达到，重复执行步骤3)～步骤7)，否则输出最优位置。

本文提出的HBOA算法将SVM识别率作为适应度函数，对SVM的惩罚因子和核函数参数进行优化，当HBOA算法满足迭代结束条件时，SVM模型也完成训练。

2.4 混合滤波器优化的调制识别算法模型

本文将雷达信号预处理为时频图像后，采用三通道结构，设计二级级联滤波器，搭建特征值映射网络，提取多角度融合特征，并联合交叉变异思想提出混合蝴蝶优化算法，寻优SVM组合控制参数，提升少数样本下的雷达信号调制识别性能。混合滤波器优化的调制识别算法训练及应用结构如图5所示，具体步骤描述如下:

图5 调制识别算法训练及应用结构

1)获取雷达信号数据集，产生9种调制雷达信号数据集；

2)根据式(1)将步骤1)获取的雷达信号转换为时频图，并按一定比例划分训练集与测试集；

3)提取雷达信号时频图特征。将训练集时频图作为EMN的输入，根据步骤①～步骤⑥设计2阶段混合滤波器，提取时频图特征，输出雷达信号时频图的特征向量；

① 根据式(3)～(5)分别设计时频图RGB通道的第1级LPP滤波器；

②根据式(6)分别将时频图与步骤①设计的滤波器卷积，获得第1级三通道特征；

③ 利用步骤②的输出，根据式(3)～(9)设计R通道第2级LPP滤波器，根据式(9)～(11)设计G通道第2级PCA滤波器，根据式(12)～(14)设计B通道第2级LDA滤波器；

④ 将步骤②的输出分别与步骤③设计的对应通道滤波器卷积，获得第2级三通道特征；

⑤根据式(16)、(24)将步骤④产生的三通道特征融合，获得特征矩阵；

⑥根据式(17)及(18)对步骤⑤产生的特征矩阵哈希编码，并根据式(19)输出特征向量；

4)依据步骤3)提取步骤2)中训练集的特征向量作为SVM的输入，并按照2.3.3节的步骤1)～步骤8)优化SVM的惩罚因子和核函数参数，同时输出SVM模型。

在实际应用中，接收雷达信号，根据式(2)转换为时频图像，按照步骤3)提取图像的特征向量，输入到步骤4)所训练得到的SVM模型完成特征分类，获取雷达信号识别结果，实现雷达信号调制识别。

3 仿真与性能分析

3.1 仿真参数设置

为了验证所提雷达信号调制识别算法性能，本文产生9种不同调制方式的雷达信号数据集，如表1所示。具体仿真参数如表2所示，其中载频、频率序列等参数根据范围随机产生，并设定信号预处理方式为CWD。

表1 样本集构成表

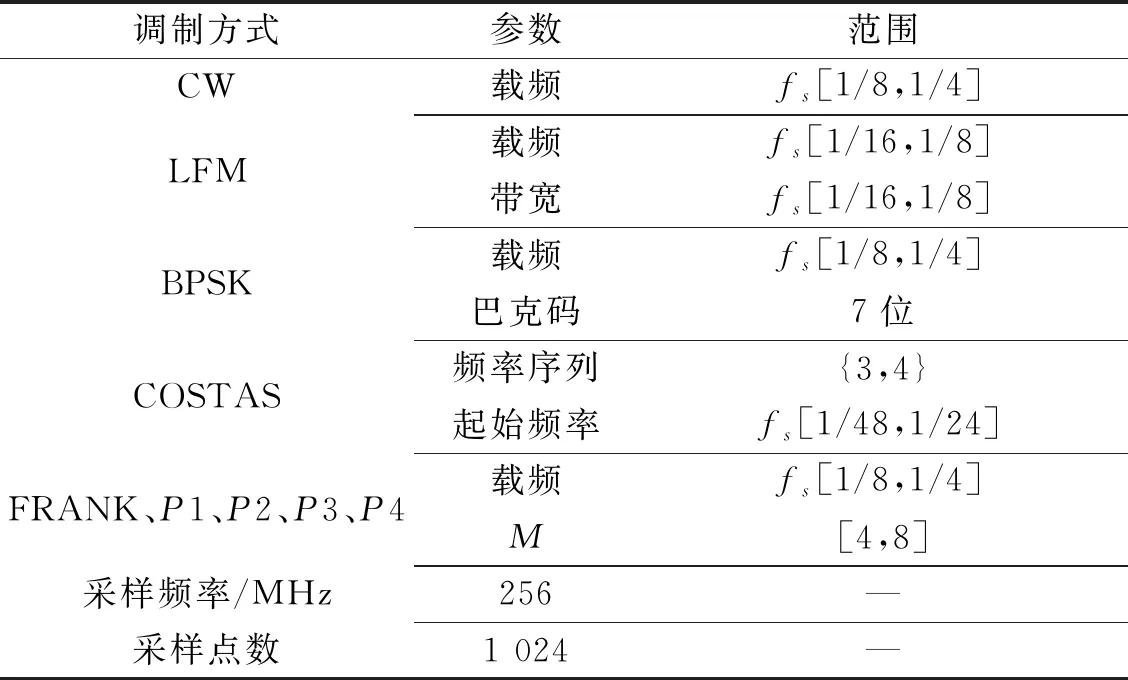
表2 信号参数表

3.2 仿真性能分析

图6给出了用网格搜索法优化SVM参数的情况下，设计不同滤波器的雷达信号调制识别率曲线，其中，EMN为本文设计的混合滤波器的特征值映射网络，LPP-LPP、LPP-PCA及LPP-LDA分别代表网络第1级利用LPP算法设计滤波器，第2级分别用LPP、PCA、LDA设计混合滤波器构建网络。

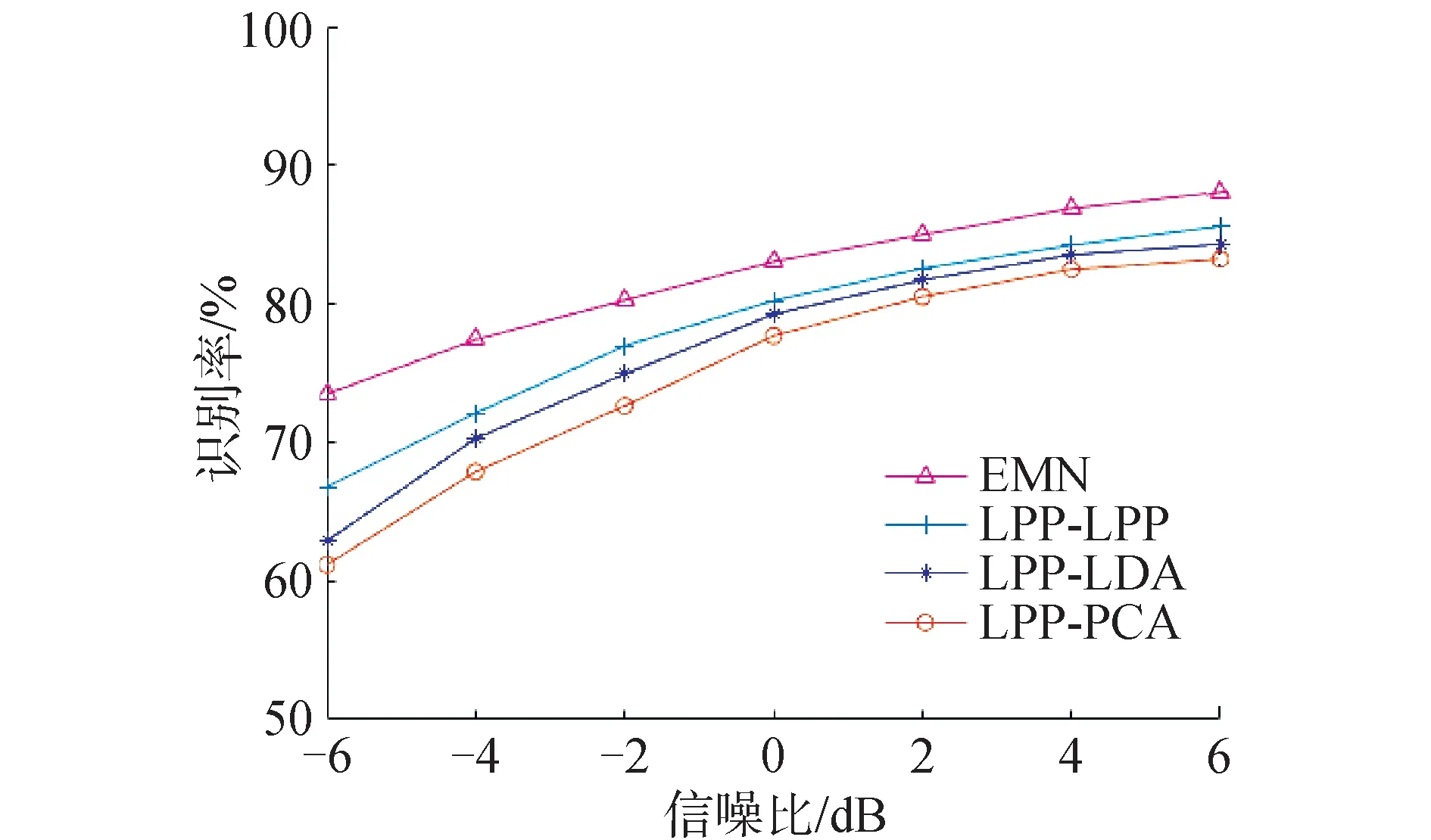
图6 不同网络识别率对比曲线

仿真结果表明，在相同信噪比的情况下，本文设计的EMN明显优于其他3种，其中LPP-LPP识别率始终比LPP-LDA和LPP-PCA高。这是由于LPP算法既具备非线性算法的长处，又可保留线性算法的特点，且设计的混合滤波器通过融合多角度特征的方式综合了3种单一滤波器提取图像特征的优势，优化了单一滤波器，增强图像表征能力，更适合提取样本数少的雷达信号时频图特征。

图7给出相同训练样本下，SVM在DE算法，BOA算法、网格搜索法及HBOA算法下的适应度迭代曲线。其中，适应度值即每次迭代后的识别率。

图7 4种智能算法适应度曲线

仿真结果表明，HBOA算法具有较强跳出局部最优的能力。从收敛速度看，HBOA算法经17次迭代达到最佳适应度值，DE需25次迭代才可达到最佳适应度值，而网格搜索法要33次迭代才可达到最佳适应值，说明HOBA算法整体上收敛速度仅次于BOA；从最佳适应度值来看，HBOA最佳适应度值最高，为0.901 9，比BOA算法高0.027 9。这是因为HBOA算法利用柯西变异算子改变BOA算法位置更新方式，并引入差分进化算法中的信息交互行为，优化了其全局寻优能力，所提算法可以提升分类器的性能，进而提高雷达信号调制识别率。

为检验所提调制识别算法在少量样本条件下识别效果，表3给出0 dB条件下不同训练样本数目时的测试集识别率，其中每种训练样本信号分别取20、30、40、50、60个，测试样本为每种信号30个。

表3 不同训练样本数目时测试结果

由表3可看出，所提识别算法的识别率与信号训练样本数目成正比，当样本数目为40个时，识别率可达85.56%，并且随着样本数目减少，识别率逐渐降低，当样本数目为20个左右时，识别率降为61.48%，这是由于训练样本数目过少，与网络参数规模失配，导致其泛化性能下降。因此本文所提算法对样本数目少的雷达信号适应性较强，但存在一定极限，当训练样本数小于该极限时，将无法训练网络。

图8给出相同条件下，采用本文所提识别算法、文献[6]中基于CNN的识别算法及文献[7]中基于PCANet的识别算法在设定的仿真参数条件下，识别率随信噪比变化的性能比较。

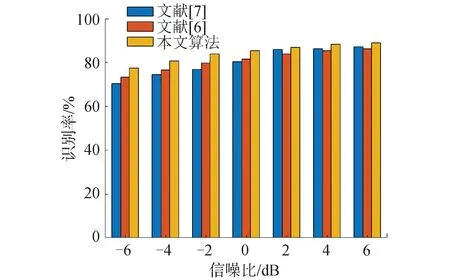
图8 本文所提算法与文献[6]及文献[7]识别率对比

仿真结果表明，在类样本数为60的情况下，本文所提算法明显优于文献[6]和文献[7]。其中，当信噪比小于0 dB时文献[7]所提算法的识别率明显低于另外2种，这是因为PCANet抗噪声性能不佳，雷达信号调制识别效果变差；在信噪比为-6 dB时本文所提算法识别率高达77.78%，相比于文献[6]提升了5%左右，其原因是文献中CNN需要大量样本训练，少量的雷达信号样本无法满足其训练需求。本文所提算法在低信噪比下表现优异，结构简单，网络参数少，仅需少量样本即可达到较高识别率，具备较好抗噪声性能，更适合小样本的雷达信号。

4 结论

1) 设计混合滤波器的特征值映射网络模型，省去了神经网络需要充足样本的训练过程，解决了样本数少情况下算法架构及参数设置不当导致调制识别率低的问题。

2) 提出混合蝴蝶优化算法，改进蝴蝶位置更新公式，使得算法能有效收敛且复杂度不会明显增加，提高了SVM的识别性能。

3) 在类样本数仅60的训练条件下，所提算法在信噪比为-6 dB时识别率达到77.78%，与其他算法相比，更适合于小样本的雷达信号调制识别。

因此，所提算法具有良好的理论和工程实用价值。后续工作将会关注所提算法在不同类型噪声环境下的应用，进一步推广其适用范围。