基于双目结构光的肝脏表面三维重建系统标定研究

张峰峰， 陈龙， 杨欣荣， 薛峰， 孙立宁

(1.苏州大学 机电工程学院，江苏 苏州 215006； 2.苏州大学 苏州纳米科技协同创新中心，江苏 苏州 215123； 3.复旦大学附属中山医院 肝外科肝癌研究所， 上海 200032； 4.中国铁道科学研究院集团有限公司 铁道建筑研究所， 北京 100081)

开放式肝脏肿瘤切除手术是目前治疗肝脏肿瘤最有效的方法之一[1-3]。从医生角度出发，如果能在术中无辐射条件下快速获取肝脏表面三维信息进行三维重建，将有助于医生实时观察肝脏表面切割状况，可以较大程度上规避肝脏被误切的风险[4-6]。基于双目结构光的肝脏表面三维重建的方法可以为医生提供术中重建的肝脏表面，但在三维重建之前，需要完成肝脏表面三维重建系统的标定。肝脏表面三维重建系统的标定精度直接影响后续肝脏表面三维重建的精度。

目前尚未有成熟的面向肝脏表面三维重建的系统标定方法。传统的标定方法在实际标定过程中存在着标定流程复杂、标定精度低、求解计算复杂等问题[7-8]。相机的标定相对比较成熟[9]，通常以基于张正友的标定方法为主流[10]。然而投影仪的标定却相对复杂，目前常用的投影法存在较大弊端。主要存在的问题在于其提取的棋盘图像的角点或圆形图像的圆心的亚像素精度较低，导致最终的投影仪标定精度较差[11-12]。王衡等[13]利用投影法进行投影仪标定，取得了一定的效果，但从整体精度来讲，该标定方法无法满足术中肝脏三维重建系统的要求。YANG等[14]也利用了类似的方法完成了相机投影仪系统的标定，但是结果依然不尽人意。除此以外整个系统标定还需要对投影仪和相机的标定参数进行组合优化，这样才能保证最终系统的标定精度[15-16]。

针对上述问题，本文主要根据实际手术过程中的需要，提出了一种针对肝脏表面三维重建系统的标定方法。从实际的手术过程中的肝脏表面三维重建系统的硬件之间的位姿关系入手，对手术视场进行分析。针对标定过程中存在的解相困难、标定板质心求解复杂等问题进行深入分析和研究，提出相应的解决办法。在此基础上搭建肝脏表面三维重建的实验平台，通过标定实验来对本文提出的方法进行验证，并且对系统的标定参数进行整体优化。

1 双目系统标定方法

1.1 双目模型及手术视场分析

在肝脏表面三维重建系统中双目相机和投影仪之间摆放的位置对手术过程中肝脏表面三维重建的精度和完整度有着重要的影响。在基于双目结构光的肝脏表面三维重建过程中，一般双目相机的摆放位置按照其光轴是否相交可分为平行双目模型和相交双目模型。平行双目模型最大的优点在于左右相机之间的几何关系简单，计算方便。但是考虑到实际的手术过程中肝脏表面三维重建会需要较广的手术视野，此时平行双目模型的视野不符合要求，因此选择视野更加宽阔的相交双目模型。这样可以保证在手术区域范围内左右相机能够捕获更多的公共视场下的投影仪投射的条纹光栅。

如图1所示为手术过程中双目结构光系统的视场示意图，在相机视场中只有左右相机、投影仪三者的公共重叠视场才可以作为肝脏表面三维重建的范围。已知左相机的视场范围为AF,右相机的视场范围为CH，投影仪有效视场范围为IK，因此只有图1中阴影部分IJK构成的区域为肝脏表面三维重建的有效区域。若是超出该区域则会破坏结构光相位的单调性，影响后续的相位立体匹配，导致肝脏表面的部分区域无法三维重建。

图1 手术过程中肝脏表面三维重建的有效视场分析

1.2 双目模型及手术视场分析

双目相机主要由2个单目相机组成，双目相机的内参标定可以简化成2个单目相机的内参的标定。假设肝脏表面三维空间中存在一点P，则跟据坐标系转换关系得到P点在像素坐标系的坐标为：

(1)

式中：s表示相机的比例系数；R和T共同组成相机的外参；A表示通过相机标定出的相机内部参数矩阵；(u,v)和(XW,YW,ZW)为像素坐标和世界坐标中点的坐标。可以将三维世界坐标系建立在标定板的左上角第一个圆的圆心上。在此基础上可以求得三维世界坐标系中的点的Z轴方向的坐标值都为0，进而可以将式(1)改写为：

(2)

式中：r1、r2、r3为外参旋转矩阵的3个列向量。相机的外参旋转矩阵R通过r1、r2和r3来表示。与此同时，在制造和安装时，由于人为的操作或自身材料的限制会导致相机在标定时产生一定的误差，这就导致相机在实际的标定过程中需要进行非线性标定。通常对相机的标定精度影响较大的畸变主要是偏心畸变和径向畸变。将相机的这2种畸变考虑在内，可以得到相机整体畸变的数学模型为：

(3)

此外，还要确定2个相机之间的三维空间位置关系，即双目相机的外参。假设2个相机求得的内参分别为Al和Ar,外参数的平移和旋转矩阵分别为Tl、Rl和Tr、Rr。由于以圆形标定板中左上角建立世界坐标系，因此可以根据标定板物理尺寸来确定标定板中所有圆的圆心坐标。通过双目相机捕捉到的图像，选择与实际标定板对应的圆，分别在左右相机图像中求取该圆心的坐标。则世界坐标系和像素坐标系关系已知的情况下，可以求解出左右相机在世界坐标系中的位姿关系，整个双目系统的标定转换关系如图2所示。

图2 双目系统标定转换关系

上述世界坐标系中的点P(XW,YW,ZW),通过双目相机拍摄后，左、右相机坐标系中的点Pcl(Xcl,Ycl,Zcl)和Pcr(Xcr,Ycr,Zcr)与之相对应，根据相机坐标系转换关系可得：

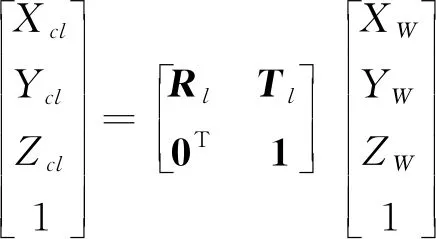
(4)

(5)

联立式(4)和式(5)可得：

(6)

式中：Rl、Tl、Rr和Tr分别为左右相机各自的旋转和平移矩阵；Rlr和Tlr为左右相机之间的旋转和平移矩阵；Pcl(Xcl,Ycl,Zcl)和Pcr(Xcr,Ycr,Zcr)分别为左右相机坐标系中的点。

由式(6)可以看出只需要求出Tl、Rl和Tr、Rr的值，即2个相机的外参数就可求得2个相机的空间相对位置关系。由于2个相机的外参数在2个相机单独标定时已求出，故可求得2个相机的相对旋转矩阵Rlr和平移矩阵Tlr。

1.3 基于三频四步法的结构光绝对相位值求解

目前投影仪标定主要有向标定板投射棋盘或圆形图案的投影法和向标定板投射条纹光栅的解相法。投影法标定投影仪主要存在的问题在于其提取的棋盘图像的角点或圆形图像的圆心的亚像素精度较低，导致最终的投影仪标定精度较差。解相法主要通过向标定板投射条纹光栅，其利用相移法求解出对应于角点或圆心的绝对相位值，从而进一步建立其与投影平面中的像素坐标的关系。该方法标定的投影仪精度相对较高。

本文采用3种不同频率的光栅条纹，有助于降低三维重建精度对相位主值的精度和光栅条纹节距大小的依赖。结合四步相移原理，如图3所示，本文采用三频四步法，共需要投射12幅不同的条纹光栅图像，图3中φi为不同频率的相位主值，Φi为绝对相位。利用多频外差法将相位主值展开，获得绝对相位，从而保证在相机拍摄的视野范围内的每个像素有与之唯一对应的绝对相位值。本文所采用的光栅条纹的频率分别为70、64和59。使用多频外差法解相的流程如下所示：

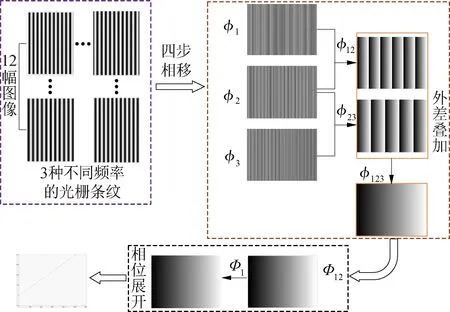
图3 基于三频四步法的绝对相位值求解

1) 相机拍摄投射的条纹光栅图像，根据相移原理对图像的相位主值求解；

2) 依据外差叠加原理，将不同频率的相位主值进行叠加；

3) 求得整个图像范围内唯一的相位频率为1的不重复的绝对相位Φi；

4) 根据周期相位Φi反推出φi的连续的相位。

1.4 基于解相法的投影仪标定

投影仪的标定所需要标定出的参数和相机一样，主要包括其内参、畸变系数以及和相机之间的外参矩阵。投影仪的结构与相机类似，在某种程度上可以看成是一种“逆相机”，但是无法和相机一样拍摄标定板图片。

1.4.1 投影仪的标定流程

“逆向机”标定主要建立投影图像坐标和三维世界坐标下的角点或圆心之间的对应映射关系。棋盘图像的角点主要由水平和竖直的线相交组成，利用解相法进行投影仪标定时，其图像的角点包含丰富的相位信息。投影仪的标定需要借助左、右相机中的任何一个相机。以左相机为例，由于棋盘图像角点处的黑白灰度差较大，产生较大的灰度跳跃，导致采集角点处的条纹光栅的效果较差。这种偏差将导致后续的条纹光栅解相的时候出现相位丢失，进而影响投影仪标定的精度。因此本文选择黑底白圆的标定板进行投影仪标定。

采用解相法进行投影仪的标定时需要通过投影仪向圆形标定板投射水平、竖直2种类型的条纹光栅，其具体的标定步骤为：

1) 调节投影仪和相机的视角，确保相机能采集到投影仪投射的光栅；

2) 调节并固定相机的曝光时间和进光量；

3) 向圆形标定板投射水平、竖直条纹光栅，并用相机进行拍摄，调节标定板位置，连续采集图像；

4) 计算出拍摄图像中标定板的圆心亚像素坐标，进而可完成相机的标定；

5) 对圆心坐标在水平和竖直方向的绝对相位进行插值进而求解出对应投影平面下的亚像素圆心坐标；

6) 重复上述步骤，最终即可完成投影仪的逆向机标定。

1.4.2 基于亚像素坐标线性插值的椭圆质心求解

从投影仪标定的流程中可看出标定板圆心的亚像素坐标的求取异常重要。相比于棋盘图像，圆形标定板的圆心周围的灰度差较小，故其圆心对应的绝对相位值求解的精度较高。为了提高投影仪的标定精度，需要对相机拍摄的图像的圆心进行亚像素坐标求解。由于相机成像的问题，在相机拍摄的图像中的圆形近似成椭圆形，因此需要对椭圆的圆心进行拟合来求解其圆心的亚像素坐标。椭圆的圆心相对圆的圆心求解较为困难，因此本文采用椭圆的质心来近似代替圆心，从而在保证精度的前提下减少复杂的求解操作并提高求解计算的速度。

在进行椭圆质心求解的时候，需要划分椭圆的窗口区域，对窗口区域内的椭圆进行图像的二值化处理。假设该窗口区域仅包含一个椭圆，通过m、n来表示对应的行和列的序列号，选择一个合适的阈值TI作为图像二值化的标准，则根据图像二值化的方法对其处理后的灰度值为：

(7)

式中：I(m,n)表示窗口内对应的像素点的灰度值。根据椭圆的质心求解公式可解得其质心坐标为：

(8)

根据计算出的椭圆质心的像素坐标，此时便可对相机进行标定。由于用椭圆的质心代替椭圆圆心，因此可以进一步求解出圆心的亚像素坐标。本文的相位展开方法主要针对像素级的像素点对于亚像素级的椭圆圆心无法实现相位展开，需要凭借插值法对相机图像中圆心周围的像素进行插值才能进一步相位展开。

假设如图4所示相机图像中的亚像素圆心相邻的4个像素点分别为(uce,vce)、(uce,vce+1) 、(uce+1,vce) 和(uce+1,vce+1) ，从水平、竖直方向对4个像素点分别进行相位展开，则投影仪图像中的椭圆圆心的亚像素坐标(ucp,vcp) 可根据水平和竖直2个方向的相位展开求得：

图4 亚像素坐标的线性插值

(9)

2 实验与结果

2.1 肝脏表面三维重建系统实验平台的搭建

2.1.1 双目相机的参数计算及选型

相机的选择对肝脏表面三维重建起到至关重要的作用，结合重建精度的需求和成本2方面考虑，本文选择型号为MER-125-30UC-L的相机。相机只可采集有限视野范围内的图像，因此相机的选择需要根据实际的使用要求确定。本文中根据医生提供的实际的相机采集到的手术区域范围达到S=30 cm×30 cm 即可完全满足需求，相机安放的位置距离手术区域大约为H=60～120 cm。相机的焦距f计算公式为：

(10)

式中：F为相机感光原件的物理尺寸。根据上述的手术区域面积及高度等要求，最终计算后选择焦距为f=8～12 mm，选择镜头的型号为C08F16-5MP。

2.1.2 肝脏表面三维重建系统的硬件组成

肝脏表面三维重建的硬件平台主要由图5所示的显示器、工作站、投影仪、双目相机、滑动支架、支撑架、手术器械、猪肝等组成。每个硬件的参数/型号和具体的作用如表1所示。

图5 基于双目结构光的肝脏表面三维重建系统硬件平台

表1 肝脏表面三维重建平台硬件作用及参数

2.2 肝脏表面三维重建系统的标定实验

2.2.1 双目相机内、外参标定实验

本文采用圆形标定板进行标定，该圆形标定板主要由19×15个圆组成，其中圆形距为10 mm。圆形标定板中包括5个用于确定世界坐标系的大圆以及用于圆形特征点检测的280个小圆。如图6所示，调节标定板的位置，使其能够清晰、完整地出现在双目相机的视野范围内，用双目相机拍摄标定板。不断改变标定板的位姿，使其始终出现在双目相机的视野范围内，双目相机同时拍摄20组标定板的图片。

图6 双目相机采集标定板图像

对相机拍摄的上述图像分别利用OpenCV库中的函数对其进行椭圆和其圆心的拟合，最终拟合的结果如图7所示。从拟合的效果可以看出大部分的椭圆拟合成功，在标定板的边缘也存在极少数的拟合失败，但这对实际的标定结果的影响可以忽略不计。

图7 标定板的圆心检测

双目相机的最终标定结果为：

双目相机标定的误差主要依靠重投影误差的平均值来衡量，凭借已经经过标定得到的双目相机的系统参数以及标定板圆心的坐标，计算出理论上的圆心坐标值。通过将标定板中实际的圆心的坐标值与理论上的坐标值来作差计算，将二者的差值作为重投影的误差值。对重投影误差求取平均值作为相机和投影仪的平均标定误差。

2.2.2 投影仪及系统外参标定实验

将双目相机和投影仪的位置进行固定，调节相机的光圈和曝光时间，使相机能够拍摄到完整清晰的图像。投影仪的“逆相机”标定需要借助左、右相机中的任意一个，二者构成类似双目系统。以左相机为例。通过投影仪将已制定好的条纹光栅投射至标定板上，利用左相机采集此时的图像，如图8所示，右下角为标定板中圆形的放大图。调整标定板的位置，不断利用相机采集标定板表面的图像。

图8 基于结构光扫描的标定板放大图

将上述相机拍摄的图片中的圆提取出来，如图9中黄色的方框框选区域，在此基础上将该圆按照椭圆的圆心拟合的方式来拟合出圆心。对提取的椭圆进行如图9中白色方框框选的区域进行图像二值化处理，从而进一步求出图9中紫色方框圈出的椭圆的质心。根据椭圆质心标定左相机，再对相机图像中的亚像素圆心周围的像素点进行插值解出绝对相位。从而求解对应的投影面的圆心的位置，完成投影仪标定，其最终标定的结果如表2所示。

表2 投影仪标定的参数结果

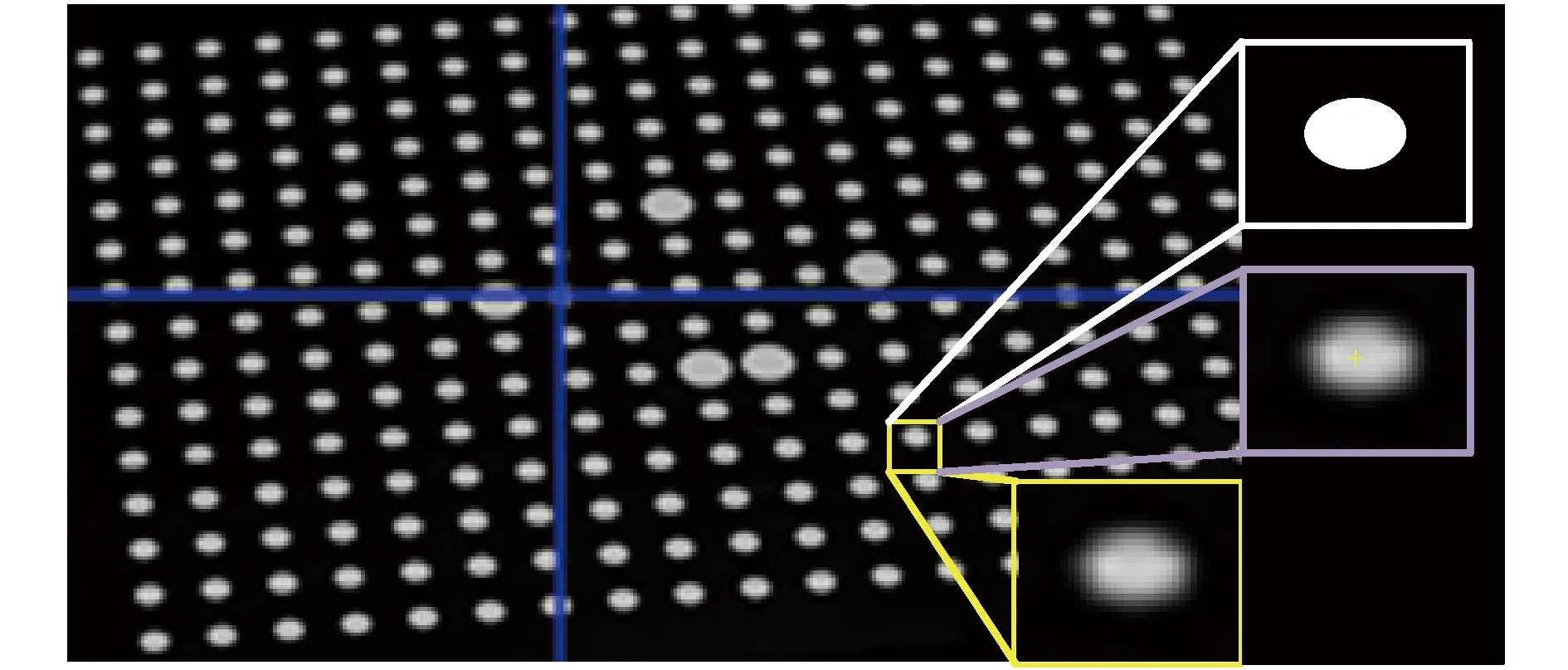
图9 椭圆的圆心拟合

将投影仪看成逆相机后，通过依赖左相机完成投影仪内参标定进而可以得到投影仪和左相机之间的位姿关系。左、右相机之间的位姿关系在双目相机标定实验中便可求出，因此最终的系统标定参数如表3所示。

表3 系统外参标定结果

2.3 肝脏表面三维重建系统标定优化及误差分析

2.3.1 系统整体参数的标定优化

以圆形标定板某个圆为例，假设利用投影仪投射结构光至标定板后，对应该圆的结构光经过三频四步解相法后获得的投影仪图像坐标为(up,vp)。与此同时相机图像中拍摄的该圆的坐标为(uc,vc),该圆的实际三维世界坐标为(XW,YW,ZW)。采用基于Levenberg-Marquardt的非线性最小二乘法对系统的整体参数进行优化。对经过优化后的系统标定误差进行统计，最大的标定误差为0.098 mm,整体的均方根误差为0.084 mm。

为了进一步验证该系统的标定精度，通过将标定板移到5个不同的位置，对其进行系统重新标定。由于标定板放在水平面上，暂设置其世界坐标中的Z坐标为0，使用标定板上所有圆坐标(xci,yci)测量值与理论值(xi,yi)的偏差表示系统的测量误差，具体的误差测量数据如表4所示。

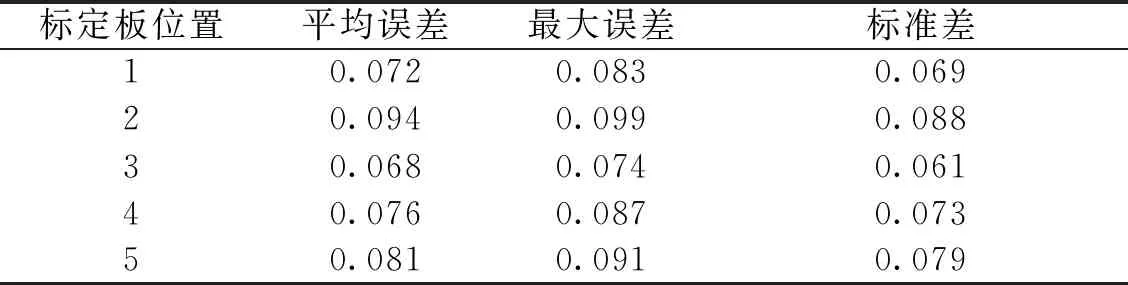
表4 肝脏三维重建系统的标定精度

从表4中的实验数据可以看出，基于双目结构光的肝脏表面三维重建系统的平均标定误差为0.078 mm,且最大误差不超过0.1 mm。

2.3.2 系统误差分析

针对上述5组实验，在每组实验中随机选取50个标定的圆心坐标的误差进行分析。从图10可以看出5组实验选取的圆的标定精度平均值在0.07 mm左右，而且误差最大和最小值之间相差较小，最高的精度达到0.05 mm左右。

图10 肝脏三维重建系统的标定误差

从图11所示的误差曲线变化图中可以清晰看出本文提出的肝脏表面三维重建系统的标定仍然存在一定的误差，并且该误差会有轻微的波动。在整体系统的标定精度稳定的同时，存在极少数的标定点的误差相对较大。

图11 肝脏三维重建系统的标定误差变化曲线

3 结论

1)针对术中双目结构光肝脏表面三维重建系统，本文提出一种高精度的系统标定方法。根据实际的手术环境，研究系统各组成硬件之间的位姿关系，制定了系统的标定流程。

2)通过实验验证，本文提出的方法的标定精度达到0.078 mm，完全符合医生的实际需求。